基于EEMD和Bi-LSTM算法的齿轮泵行星轮典型故障诊断

高美真，高烨童

（1.焦作师范高等专科学校信息工程学院，河南焦作 454000；2.西安理工大学计算机与信息工程学院，陕西西安 710061）

随着自动控制技术的快速发展，工业物联网也获得了广泛应用，可以高效收集大量的设备运行故障，通过传统故障分析方法已无法实现及时处理这种大数据故障信息［1-4］。行星齿轮可以通过设计特定的结构来适应不同的工况条件，目前该齿轮已成为机械动力系统的一个重要组成部件，对控制设备稳定运行发挥了关键作用。通过分析齿轮运行期间的信号变化特征，可以发现存在多种不同形式的变化特性［5-7］。其中深度学习方法因具备数据自我迭代处理的效果，对多种复杂数据都能够达到快速准确提取的效果，成为大数据处理领域的一项重要应用技术，已被用于语音信号处理、图像分析等领域［8-10］。

相关方面的研究吸引了很多学者。王惠中等［10］则根据长短时记忆神经网络（long short-time memory，Bi-LSTM）方法在时间序列提取的独特优势，综合运用LTSM与softmax分类器方法对各类故障信号进行诊断分析，同时设计了相应的仿真实验，对该方法的有效性进行验证。国内学者胡茑庆等［11］开展了智能诊断方面的研究工作，利用经验模态分解方法对度数据进行处理，再通过深度卷积神经网达到诊断的要求，测定行星齿轮泵齿的振动信号并验证了该方法实际诊断效果。Hsueh等［12］综合运用经验小波变换与卷积神经网络（convolutional neural networks，CNN）相结合的方式进行故障诊断，同时利用该方法验证了感应电动机的运行故障信号分析情况。Chen［13］通过改进循环神经网络的方式，建立了长短时记忆神经网络，以循环神经网络为基础并对前期信号实施过滤，由此克服了采用循环神经网络方法面临的无法大范围依赖学习的问题，从而实现对时序数据的高效分析。经验模态分解（ensemble empirical mode decomposition，EEMD）则根据CEEMD的运行特性与排列熵的随机检测方式，使模态混叠受到显著抑制，确保获得准确的IMF分量［14］。

本次测试在行星齿轮泵故障诊断前进，采用EEMD 和双向记忆网络相结合的模式，对4 种不同的行星轮进行了故障测试。采用EEMD 方法实施信号分解，生成相应的IMF 分量，将上述参数输入模型内进行训练得到准确分类结果，再对其他网络参数进行测试分析。

1 EEMD理论

由于EEMD 同时具备CEEMD 和排列熵在信号处理方面的优势，非常适合信号中随机参数的精确测试［12］。非平稳信号s（t）的分解步骤如下：

步骤1依次将均值为零的白噪声信号ni（t）与-ni（t）加入原始信号s（t），得到

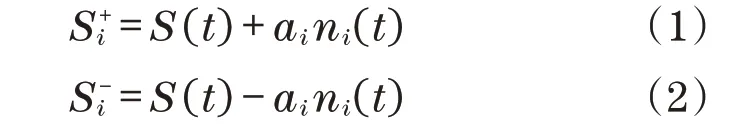
式中：ni（t）为加入的白噪声信号；ai为加入的噪声信号幅值；i取值为1，2，…，N，N为白噪声对数。

通过EMD分解获得IMF分量序列集成分量为

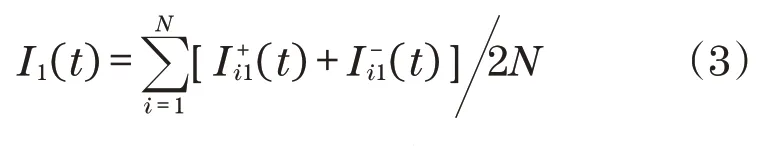
再对得到的排列熵根据各自熵值大判断I1（t）是否存在异常。进行计算时设定排列熵2 个参数，控制嵌入维数m为6，时间延迟λ为1。

步骤2当I1（t）属于异常信号时，则重新回到步骤1，直到IMF分量Ip（t）属于非异常信号为止。

步骤3从原始信号内分解得到前p-1个分量：

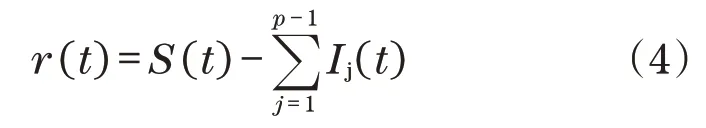
步骤4以EMD 方法分解剩余信号r（t），以频率高低顺序作为依据对IMF分量实施排列。

2 双向长短时记忆网络

2.1 循环神经网络

循环神经网络（recurrent neural network，RNN）属于递归神经网络，时间序列输出取决于前一时刻与当前输入的共同影响。

t时刻的RNN网络输出为

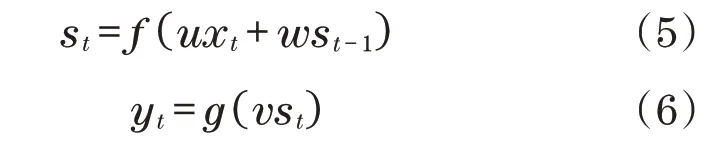
式中：t-1 为上个时刻；t为现有时刻；w为之前隐藏层相对目前隐藏层所占的权重；x为RNN 网络输入；u为输入层至隐藏层权重；y为RNN 网络预测结果；s为隐藏层状态输出。

网络在t时的总损失E为

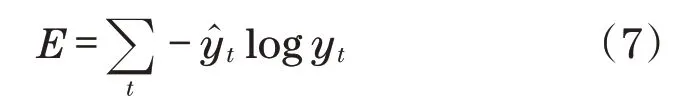
对网络进行训练时，通过参数优化算法来完成u、w、v参数的更新。参数w在t时梯度误差计算式为

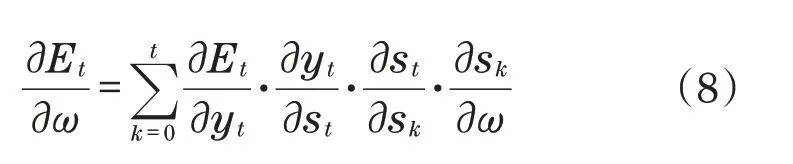
在处理深层次网络的时候，当选择参数优化模式实施更新时，将会出现局部梯度弥散的结果，严重时还会引起梯度爆炸，从而产生差异很大的网络权重，表现为网络状态的大幅波动。

2.2 长短时记忆网络

长短时记忆网络结构存在以下3个内部运行阶段。

（1）计算细胞状态遗忘信息比例：

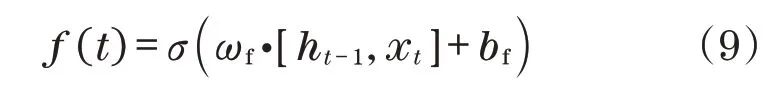
式中：ωf为遗忘门权重；按照［ht-1，xt］的形式把2个向量共同组成1个向量，σ为simoid激活函数，取值在0～1范围内。

（2）按照细胞的不同时期状态确定记忆过程并对数据进行更新。通过输入门it选择性记忆当前信息，更新后得到的细胞状态Ct内将旧信息去除后增加了2个新的细胞数据：

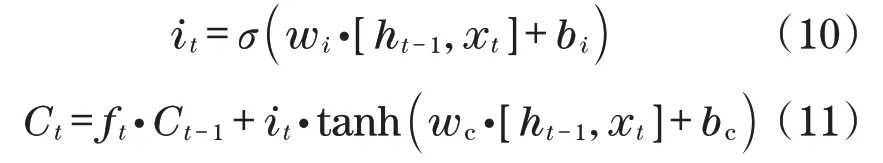
式中：wi为输入门权重；Ct为加入的信息；bi为输入门偏置；bc为新增信息偏置；wc为新增信息权重；it·Ct为新增部分的细胞信息。

（3）输出阶段。输出结果受到输出门和细胞单元状态的共同影响，通过输出门作为依据得到输出结果，进行tanh 计算实现细胞单元的处理，对其相乘计算得到

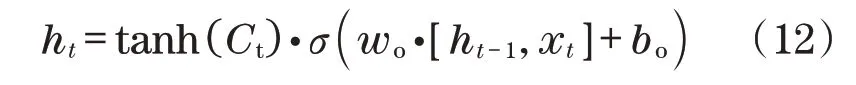
式中：wo、bo分别为输出门权重与偏置。

2.3 双向长短时记忆网络

为得到更加准确的信息，构建得到双向长短时记忆网络（bi-directional long short-time memory，Bi-LTSM），Bi-LTSM 通过时间展开计算的结果如图1所示。

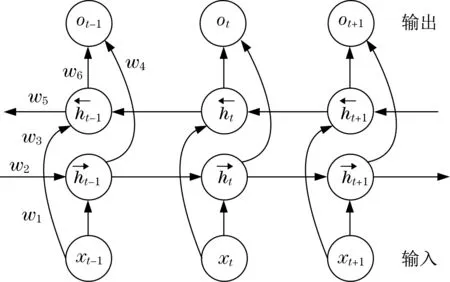
图1 Bi-LSTM网络结构Fig.1 Bi-LSTM network structure diagram

由图1 可见，当前输出受到前向层和反向层输出综合作用，以下给出了网络在t时的输出ot：

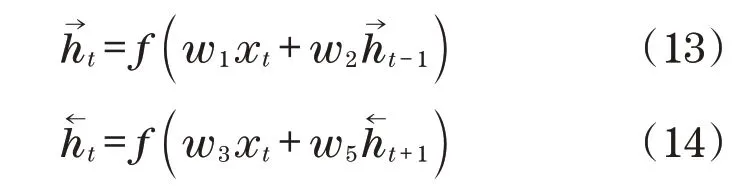
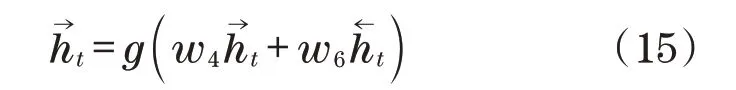
式中：w为权重；为正向隐藏层输出；为反向隐藏层输出。

3 数据处理及网络设置

3.1 数据集描述

分别对行星轮处于不同的运行状态下形成的信号数据进行采集分析。将采样频率设定在10 kHz，电机转速2 500 r/min，依次对各齿轮状态进行信号数据采集得到300组振动加速度信号，每组中存在900点数据。故障数据集描述结果见表1。

表1 故障数据集描述Tab.1 Description of the fault data set

3.2 EEMD分解

对采集得到的初始数据进行EEMD 分解获得IMF 分量，以频率由高往低的顺序排序，再将高斯白噪声加入，其标准偏差为0.2，迭代次数上限为25。本次共确定6 个IMF 分量，对齿轮不同运行状态下的信号实施分解。

利用Bi-LTSM 网络对初始6 个模态分量识别，进行模型训练时，由于分量包含了太长的数据，需要花费更长时间才能完成训练。为提升训练效率并改善精度，选择15 个时域和16 个频域特征进行分析，再将模型输入维度由1 000降低至30，进一步优化了故障特征。

3.3 参数设置

本研究构建的双向长短时记忆模型包含了1个softmax 层、1 个全连接层、1 个分类输出层、1 个Bi-LTSM 层。为全连接层设置了dropout 随机失活层，避免模型发生过拟合的问题，控制失活值恒定在0.65，并设置更多ReLU 激活层来达到加快网络训练的效果。本次模型运行环境为Matlab，Bi-LSTM网络模型参数设置见表2。

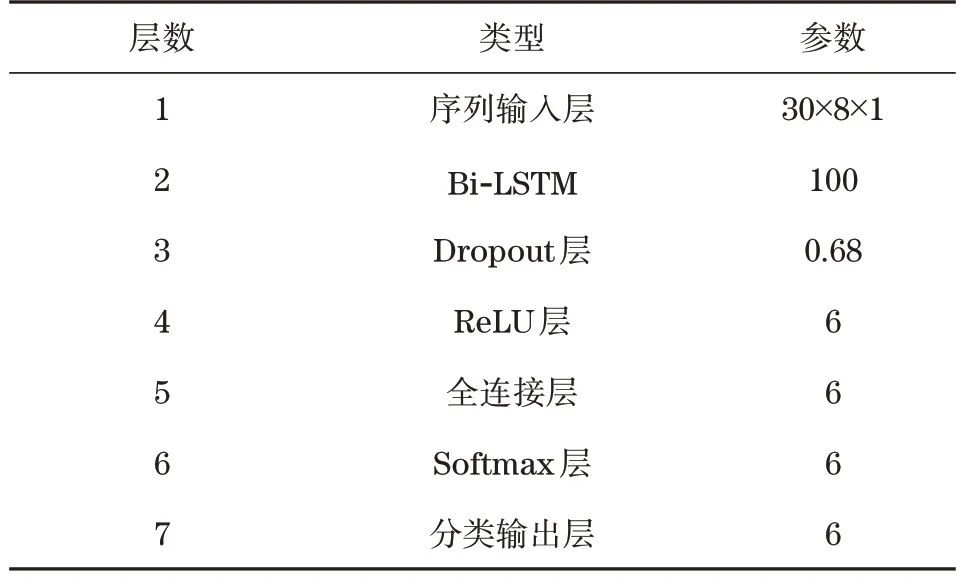
表2 Bi-LSTM网络模型参数设置Tab.2 Parameter settings of Bi-LSTM network model

测试时设定批量为100，学习率0.01，选择Adam 算法完成寻优计算。通过控制梯度阈值等于1，以防止梯度爆炸的情况；以轮数代表训练次数，共训练50 次，每个周期结束后再对网络开展一次迭代计算。本实验的网络超参数见表3。

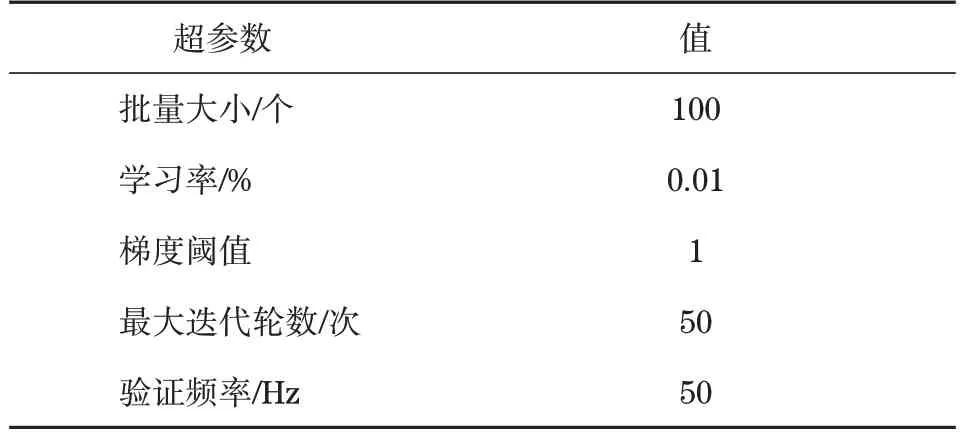
表3 Bi-LSTM网络模型参数设置Tab.3 Parameter settings of Bi-LSTM network model

4 实验结果分析

4.1 参数优化

测试时将Bi-LTSM 层节点数设置在50～200范围内，训练进度与用时如图2 所示。随着节点数持续增加，形成了先增大再降低的验证精度变化规律，诊断用时快速延长。当节点数等于200 时，网络达到了最高验证精度。

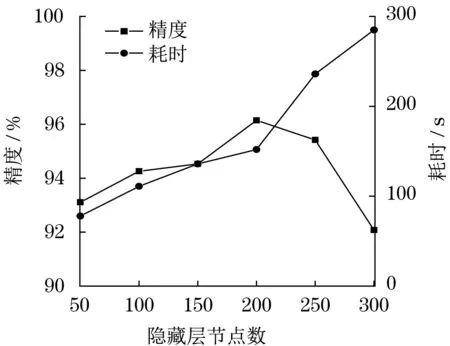
图2 模型精度、耗时与Bi-LSTM节点数关系Fig.2 Relationship between model accuracy and time consumption and Bi-LSTM node number

本次测试的网络Bi-LTSM 层数对模型精度和耗时的影响结果如图3 所示。通过对比不同层数下的Bi-LTSM 模型结果可以发现精度几乎相同，而诊断时间明显增加，综合判断认为4 层Bi-LTSM 具备最佳性能。

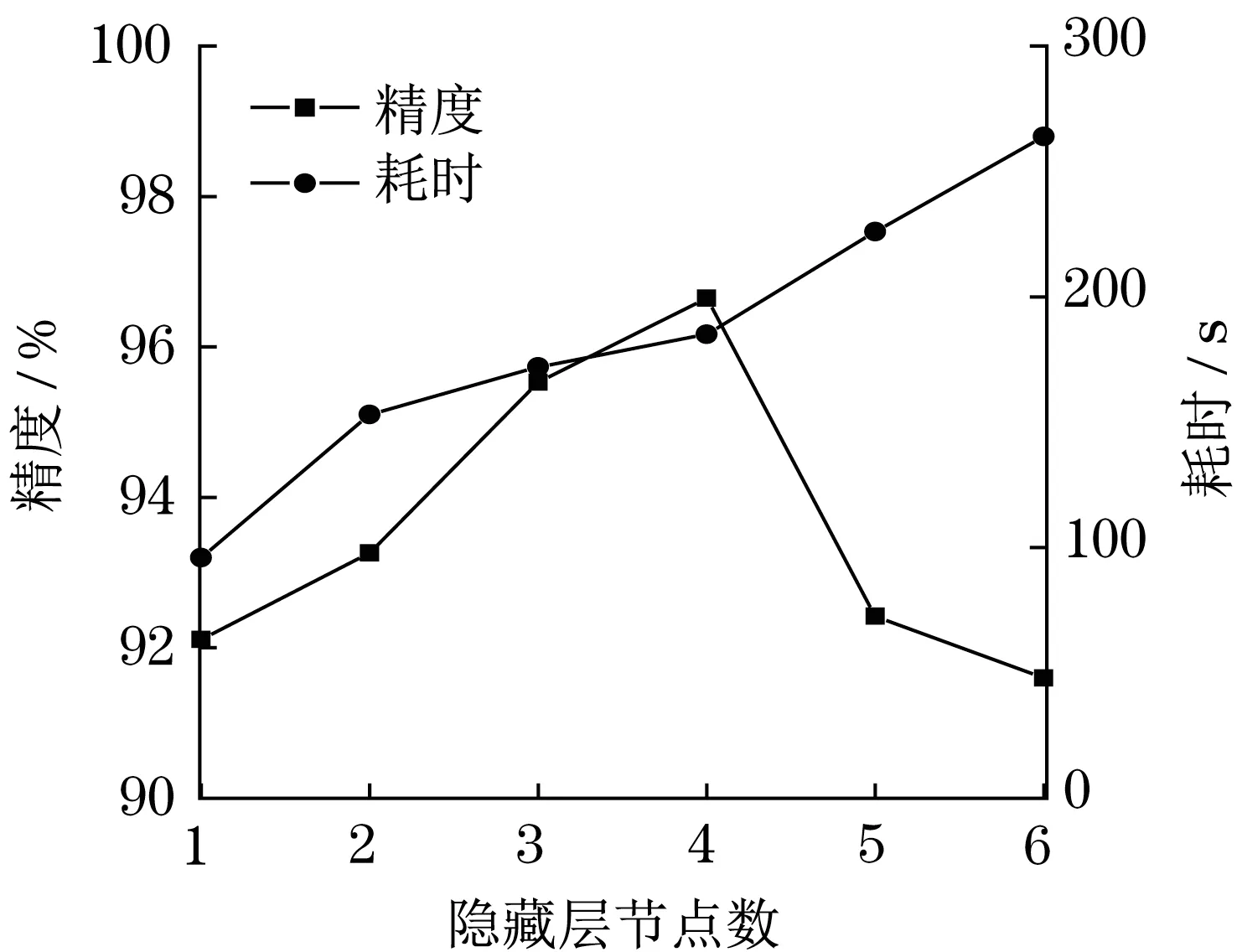
图3 模型精度、耗时与Bi-LSTM层数关系Fig.3 Relationship between model accuracy and time consumption and Bi-LSTM layers

4.2 实验结果

随机选择比例为70%的数据实施训练，再测试剩余30%的数据，图4 给出了模型训练与验证过程，可以看到在不同迭代次数下验证误差变化情况。通过测试发现该模型精度达到95.3%，进行迭代计算时形成了波动变化的训练曲线，可以推断该模型并没有达到稳定预测的效果。以图5 的混淆矩阵模型准确识别齿面形成的磨损缺陷和缺齿情况，断齿识别率94.1%，最低的是齿根裂纹故障识别率，只达到86.5%，同时发现齿根裂纹只达到了一个较低的识别率，这是由于齿根裂纹会被误判为断齿而引起结果偏差。

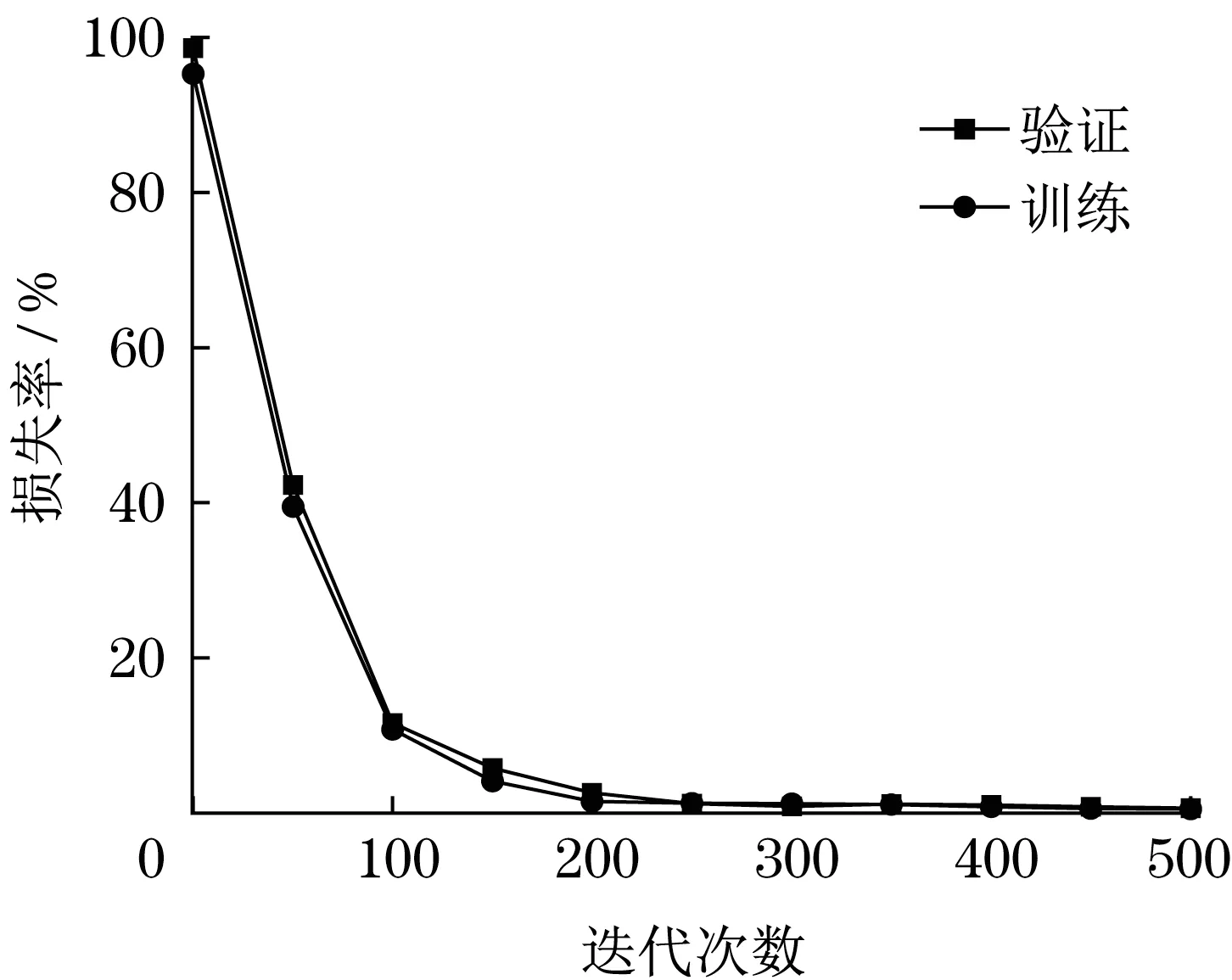
图4 模型训练损失率与随迭代次数关系Fig.4 Relationship between model training loss rate and the number of iterations

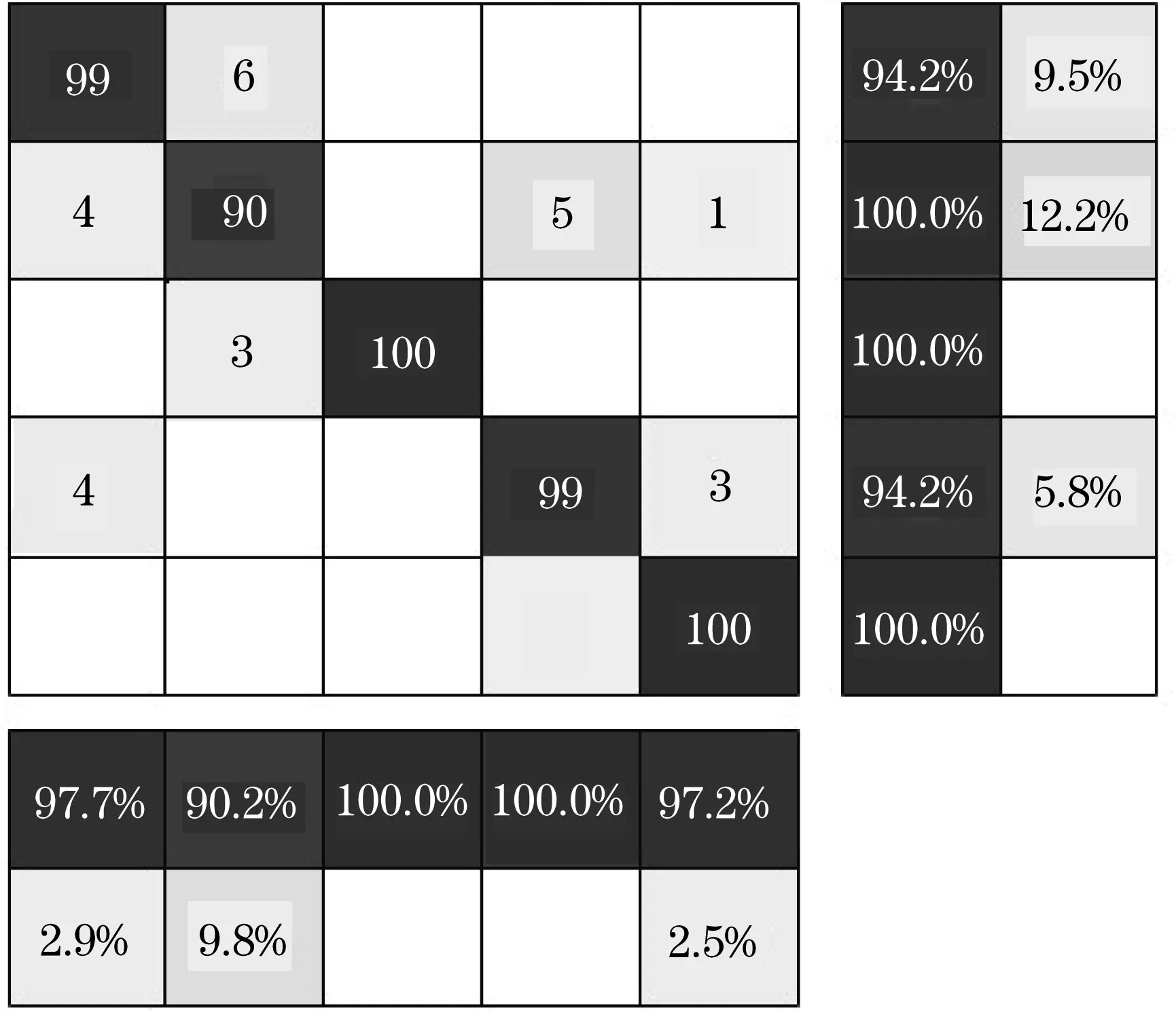
图5 模型混淆矩阵分布Fig.5 Distribution of model confusion matrix

4.3 对比分析

4.3.1 必要性验证

图6 为EEMD 处理前后模型对应的迭代精度。图中可见，未经EEMD处理的模型表现出了不稳定的测试结果，实际精度只有70%，EEMD 处理后模型精度与稳定性都发生了大幅上升。因此，Bi-LTSM 模型在时序信号处理方面具有明显优势，本次测试的初始信号呈现相对紊乱的时序特性，不能达到准确识别的效果，先对信号EEMD 分解后，可以促进所有分量都获得更优的时序性，促使模型诊断精度得到显著提升。

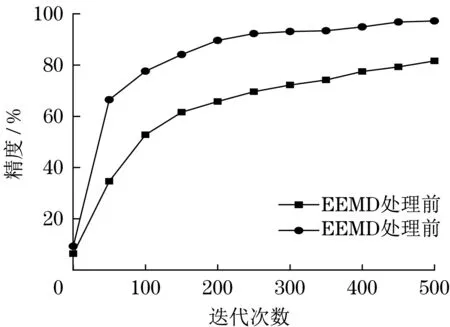
图6 模型精度与随迭代次数关系Fig.6 Relationship between model accuracy and number of iterations

4.3.2 优越性验证

图7为LTSM与Bi-LTSM网络迭代处理得到的精度变化趋势。

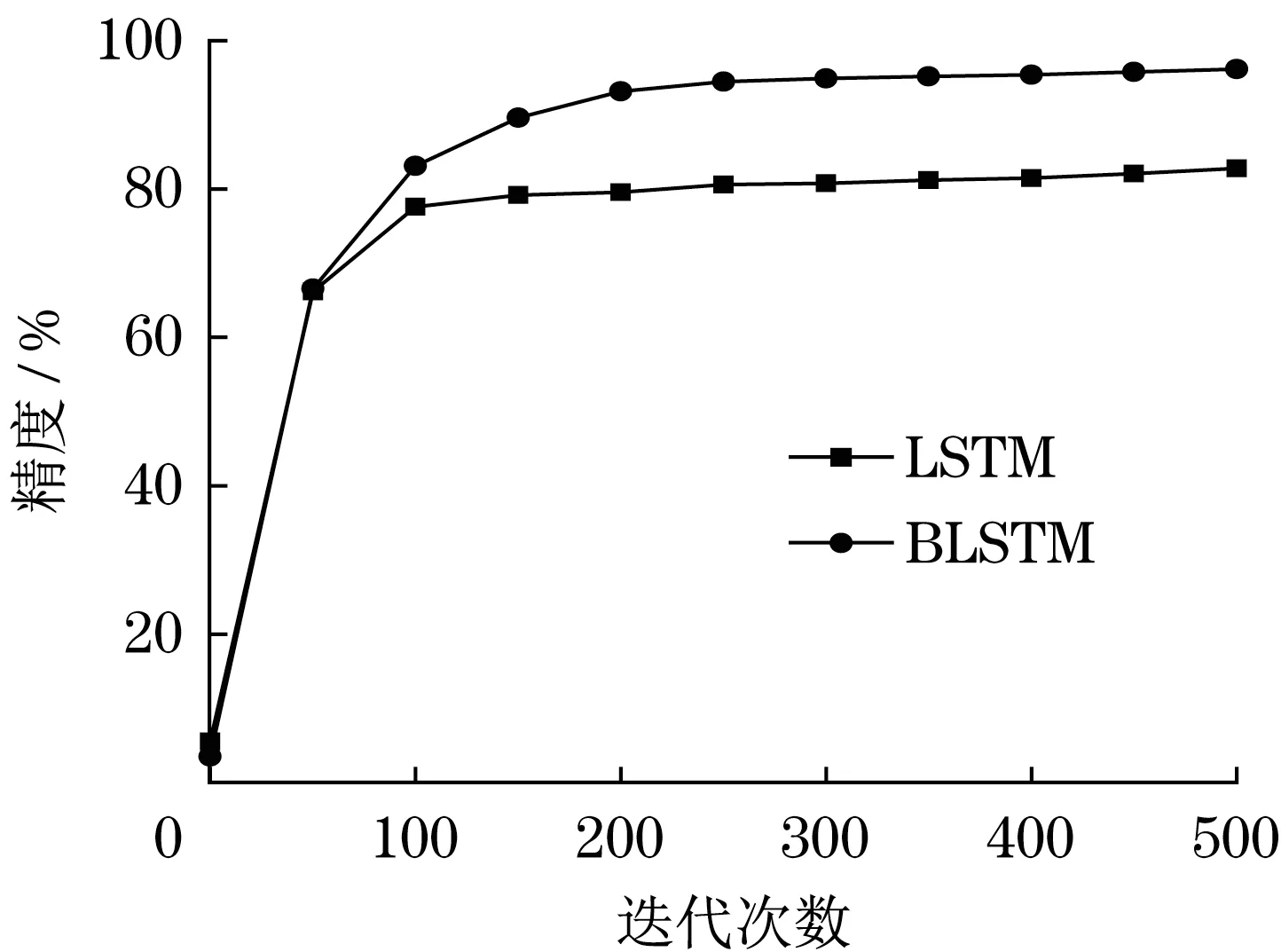
图7 LTSM、Bi-LTSM网络模型精度与随迭代次数关系Fig.7 Relationship between LTSM and Bi-LTSM network model accuracy and iteration times

在迭代的初期阶段时，LTSM 模型呈现快速收敛的特点，产生这一结果的原因为LTSM 模型属于单向的往前训练形式，Bi-LTSM 模型中共由2 个LTSM 层组成，按照前、后方式训练，效率较低。Bi-LTSM 模型到达后期迭代过程时，可以更快拟合，获得高于LTSM的验证精度。

5 结论

（1）通过模型精度和耗时的最优参数范围为节点数200和网络层数4层。

（2）本网络损失小于1%，满足良好稳定性的条件，可以实现精确识别齿面磨损和缺齿故障，断齿、正常齿轮的识别率都达到了93%以上，齿根裂纹故障识别正确率达到了86.5%。

（3）对信号EEMD 分解后，可以促进Bi-LTSM模型所有分量都获得更优的时序性，促使模型诊断精度得到显著提升。Bi-LTSM 模型到达后期迭代过程时，可以更快拟合，获得高于LTSM 的验证精度。