三机驱动远超共振机械系统的二倍频同步及其仿真研究

罗元安，胡文超，张 旭，王志辉，张学良

（1.会理县财通铁钛有限责任公司工程管理部，四川凉山 615100；2.东北大学机械工程与自动化学院，辽宁沈阳 110819）

关于同步现象，最早的探索可以追溯到Huygens 关于耦合单摆的同步研究。Blekhman［1］基于直接运动分离法提出了双激振器振动机的同步理论，并给出了同步的运动学及动力学定义；Inoue 等［2］研究了平面运动双电机驱动激振器的三倍频同步；Wen 等［3-4］运用平均法得出振动系统实现同步的同步性和稳定性理论条件，发明了大量的自同步振动机械，建立了振动利用工程的新学科；Balthazar等［5］利用数值仿真给出了2个或4个非理想激振器的自同步的简要评论，这些特殊现象被称为“sommerfeld”效应；Zhao 等［6-7］利用改进的小参数平均法推导出含有扰动参数的频率捕获方程并且得到了系统实现同步的两大判据；Zhang 等［8-9］对双机及多机驱动同步理论进行了深入的研究，在分析单质体的基础上研究了多质体同步理论，利用固有频率将整个频率区域分为若干个区间，得到各区间的耦合动力学特性。

尽管上述文献已经对2 个或多个激振器的同步理论进行了细致的探索和研究，但这些成果主要集中于以单一频率驱动各激振器进而获得其在相同转速下的同步及稳定特性，对不同频率驱动的激振器实现同步的研究却很少涉及。

本文以三机驱动远超共振振动系统（即系统的运转频率是其固有频率的3 倍以上）为例，运用渐近法对其在二倍频条件下的稳态相位差、质体运动形式等稳态特性进行研究，并在理论推导的基础上进行相应的仿真，验证理论结果的正确性。

1 系统动力学模型和运动微分方程

三机驱动机械系统的动力学模型如图1所示，弹簧对称旋转，每个激振器都由感应电机驱动，绕各自旋转中心旋转，旋转相位角分别为φ1、φ2、φ3，激振器回转轴心与质体质心的连线与x轴的夹角用θi表示，其中，θ1=θ，θ2=90°，θ3=180°-θ。系统运动有3个自由度，分别为x、y方向振动及绕质心的摆角ψ。

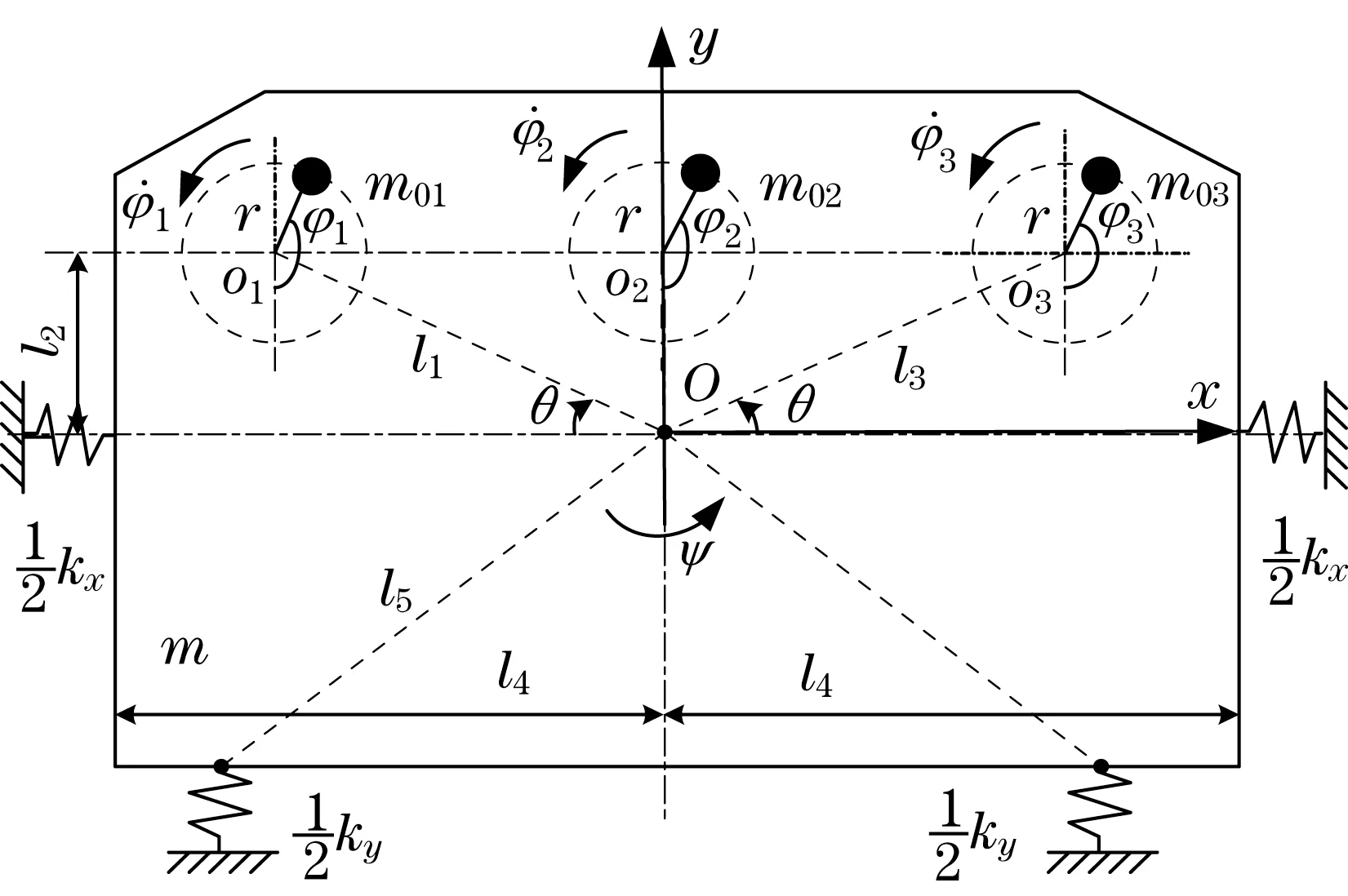
图1 三机驱动系统动力学模型Fig.1 Dynamic model of a vibrating system with three exciters

根据Lagrange方程得系统的运动微分方程如下：

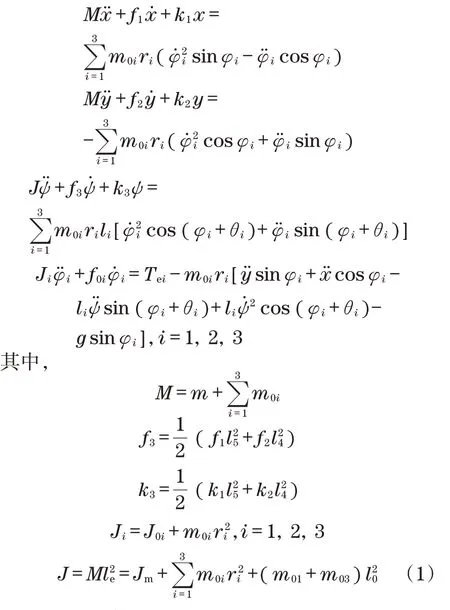
式中：Jm为质体m的转动惯量；Ji为激振器i的转动惯量；J0i为激振器i的轴转动惯量；le为系统当量回转半径；f1、f2、f3分别为x、y、ψ方向上的阻尼系数；k1、k2、k3分别为x、y、ψ方向上的弹簧刚度；Tei为电机i的电磁输出转矩。

2 二倍频同步的理论分析

3 个激振器实现同步稳定运转时激振器1 和3的运转频率相同，激振器2 的运转频率是它们的2倍，激振器旋转时的相位角为

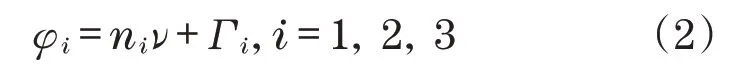
式中：ν=ωt，ω为激振器1和3的运转频率；Γi（i=1，2，3）是激振器运动产生阶段发生缓慢变化的函数，将其定义为相对相位，n1=n3=1，n2=2。将Γi写成Bogliubov标准形式［10］：

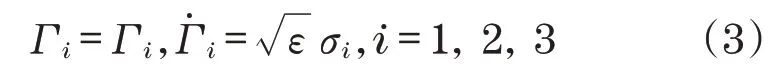
将式（2）、式（3）代入式（1）中，可得一阶联合微分方程，其表达式如下：

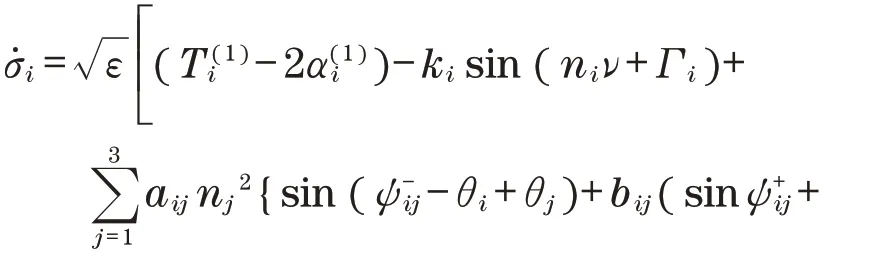
2.1 转速比为1∶1激振器间的同步条件

考虑到激振器1 和3 的转速相同，取式（5）到ε项为止，可得

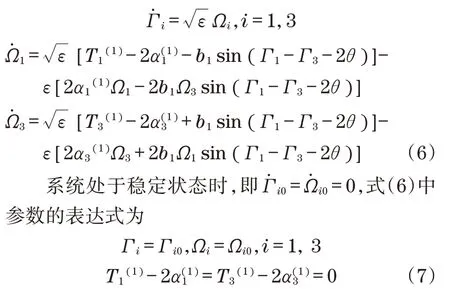
因此将式（7）代入式（6）得激振器1和3实现转速比为1∶1同步的条件为

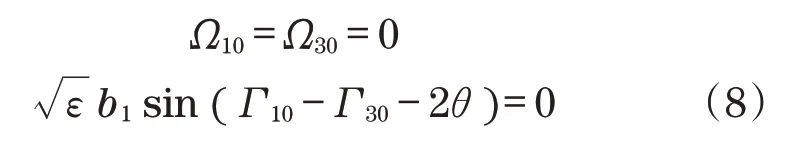
2.2 转速比为1∶2激振器间的同步及稳定条件

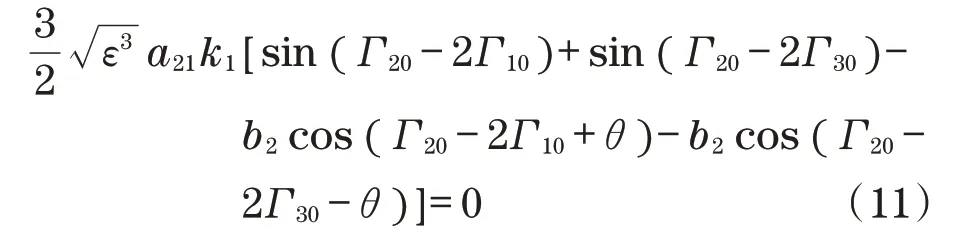
对其进行稳定性分析，因为初始相位角Γi0具有小偏差，需要做如下设定：

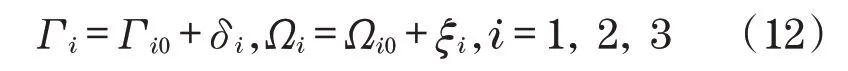
将式（12）代入式（5）中得到摄动方程表达式为

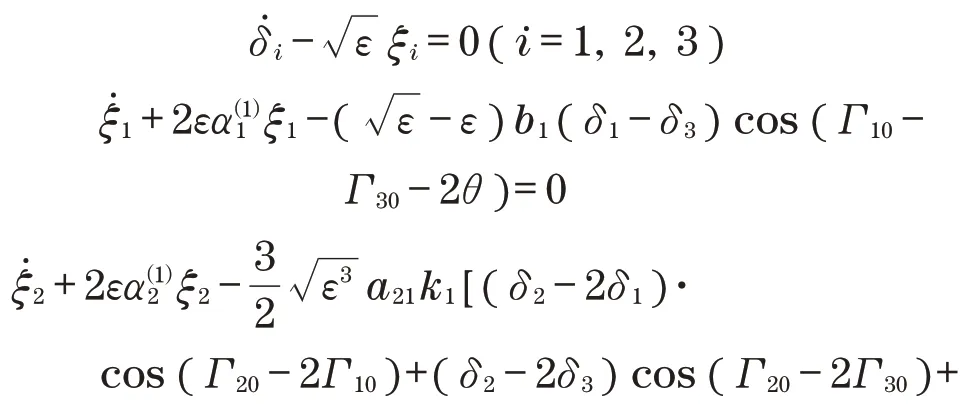
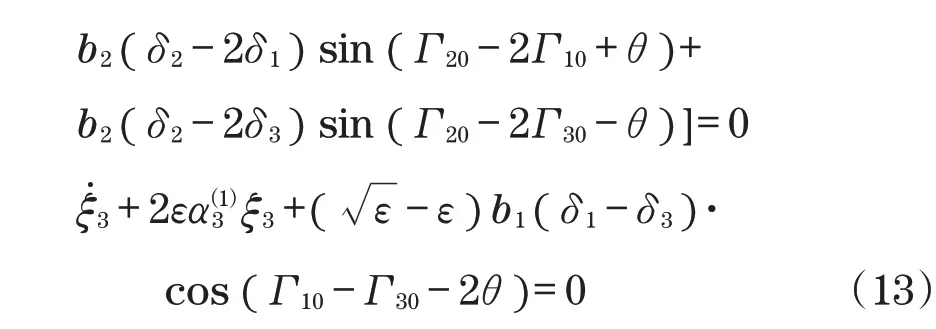
取λ为特征值，得到特征方程表达式为

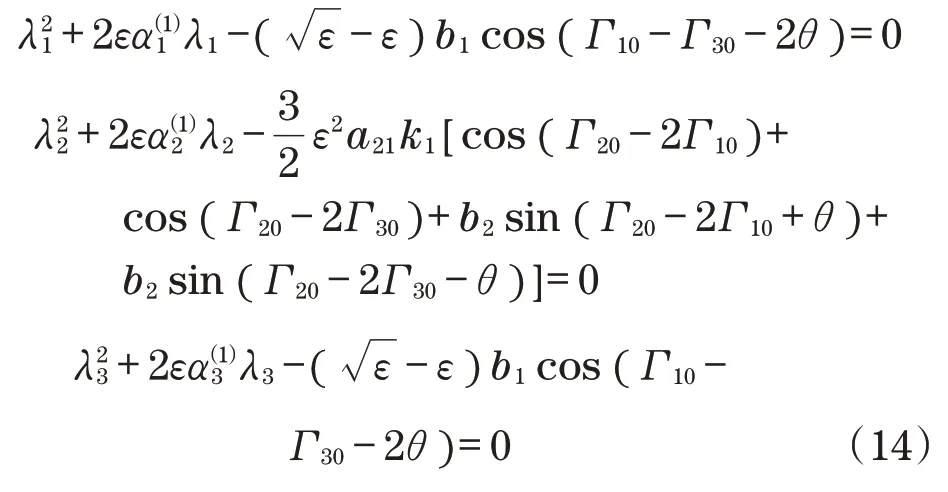
应用Routh-Hurwitz 稳定性准则，即方程的解λi(i=1，2，3)具有负实部时，系统是稳定的。所以有

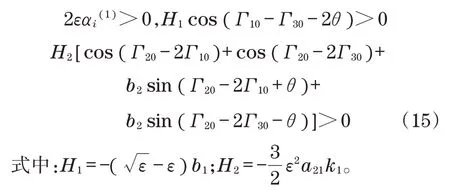
因此，式（15）为系统在二倍频同步条件下的稳定性判据条件。H1被定义为系统基频同步稳定性指数，H2被定义为系统二倍频同步稳定性指数。小参数ε是个比值，要远远小于1，所以H1=-(ε)b1恒小于0，分析式（15）可得激振器间的稳定相位差关系为

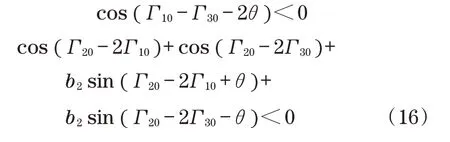
3 仿真

为了进一步验证上述理论结果，在本章中，将龙格-库塔程序应用于振动系统的运动微分方程中，对理论分析结果进行了相应的计算机仿真。3 个电机型号一致，其对应参数为三相鼠笼式，50 Hz，380 V，6 级，0.20 kW，额定转速980 r/min。电机内部参数为转子电阻Rr=3.40 Ω，定子电阻Rs=3.35 Ω，互感Lm=164 mH，转子电感Lr=170 mH，定子电感Ls=170 mH。振动系统参数为m=1 000 kg，m01=m02=m03=15 kg，r=0.15 m，k1=k2=120 kN/m，k3=80 kN/rad，J=960 kg·m2，f1=f2=3.83 kN·s·m-1，f3=3.27 kN·s·rad-1，β=40°。将电机1 和电机3 的工作频率设置为25 Hz，电机2 的工作频率设置为50 Hz，仿真结果如图2所示。

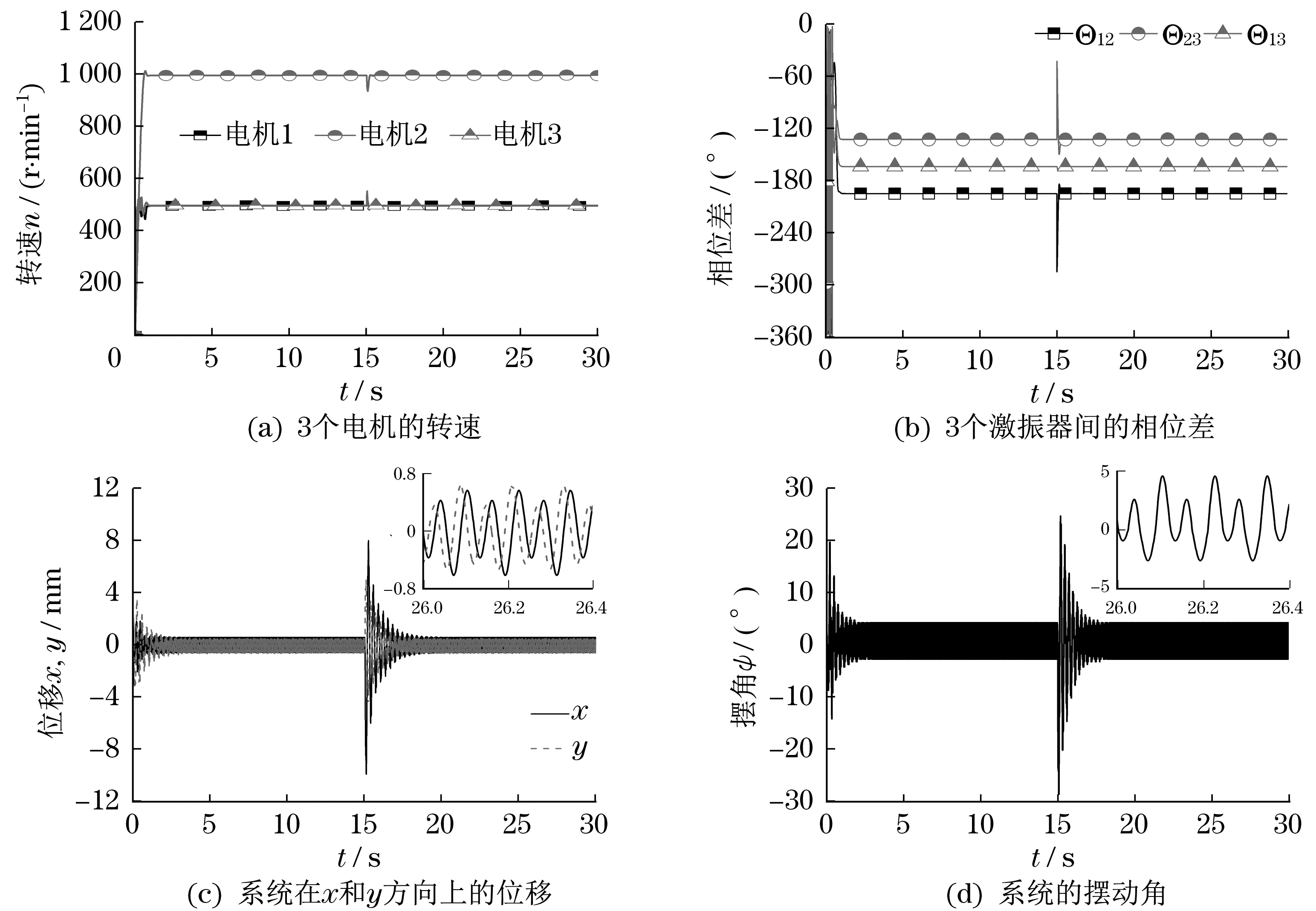
图2 三激振器同向回转的仿真结果Fig.2 Simulation results of three exciters rotating in the same direction

如图2（a）所示，由于3 电机的运转频率比为1∶2，所以对应于转速会出现2 倍关系。电机1 和3的转速相同，约为498 r/min，电机2 的转速约为996 r/min。由图2（b）可知，电机供电约1 s 后系统达到同步稳定运转，此时3 个激振器间的稳定相位差为Θ12=-194°、Θ23=-132°、Θ13=-163°，并且各激振器间的相位差能够很好地满足式（16）。图2（c）、图2（d）为各方向上测得的系统位移响应，x和y方向上的振幅分别为0.58、0.61 mm。摆动角接近5°，相对较小，因此只研究平面运动，通过位移响应的放大图可看出稳定状态下质体在各方向上的具体运动形式。其振动波形为叠加波形，这是由于高低频电机产生的不同激振力相互影响、相互作用的结果。将该研究应用到振动筛分设备上，可使筛网获得不同激振力的作用，从而筛分效果更优越。

上述仿真过程中，在15 s 处施加π/2 的干扰给电机2，从图2 可以看出电机转速、激振器间相位差和系统的响应在经过短暂波动后迅速恢复到干扰前的稳定状态，这表明3 个激振器可以在二倍频条件下同步稳定运行，并有较强的抗干扰能力。

4 结论

通过理论和仿真分析，得出以下结论：

（1）建立了一种远超共振机械系统中三机同向旋转的动力学模型，运用拉格朗日方法推导出了振动系统的运动微分方程，基于渐近法得到3 个激振器在二倍频状态下实现同步的条件。同时推导出同步状态下的稳定性判据，其结果符合Routh-Hurwitz准则。

（2）得到系统实现二倍频同步时激振器之间的稳定相位差以及各方向上的运动规律。质体的振动波形为叠加波，这种叠加波使得运动轨迹更为复杂，可为工程上振动筛分设备的功能化设计提供更多的选择和理论参考。

（3）通过仿真对理论分析进行了验证，其结果满足理论推导中相位差的稳定区域，进一步证明理论方法的正确性及所用研究方法的可行性。