吊管机工作装置的设计仿真与结构优化
裴宝浩,戴 成,于 蓬,张元元,杨 君5,
(1.烟台职业学院汽车与船舶工程系,山东烟台 264670;2.中国机械科学研究总院集团有限公司条件保障处,北京 100094;3.济南嬴氢动力科技有限公司技术部,山东济南 271100;4.淄博职业学院汽车工程学院,山东淄博 255300;5.山东交通学院汽车工程学院,山东济南 250357)
国内外吊管机的生产几乎都是在推土机底盘上加装工作装置改造而成[1]。根据某推土机底盘的具体形式,最终确定了吊管机的总体布置方案,其工作装置主要包括配重机构、变幅机构和起升机构等。配重机构的作用是提供足够大的平衡力矩,防止吊管机在起吊管道时发生倾覆[2]。由于吊管机的设计起吊质量为100 t,发生倾覆的危险很大,因此,配重机构的设计极为关键。
1 Adams模型的建立
根据计算,配重机构要实现其提供足够大平衡力矩的作用,其质心至少需要相对初始位置外移1 600 mm。检验所设计的配重机构能否达到这个要求,需要对其进行运动学分析。此外,由于配重机构自身质量很大,达到12.5 t,对承重部件和液压缸的可靠性提出了很高的要求。因此,对机构进行动力学分析,确定承重部件和液压缸的受力,也是必不可少的。利用Adams软件,对所设计的配重机构进行运动学和动力学分析[3],在此基础上,完成对配重机构的结构优化。导入Adams中的模型如图1所示。
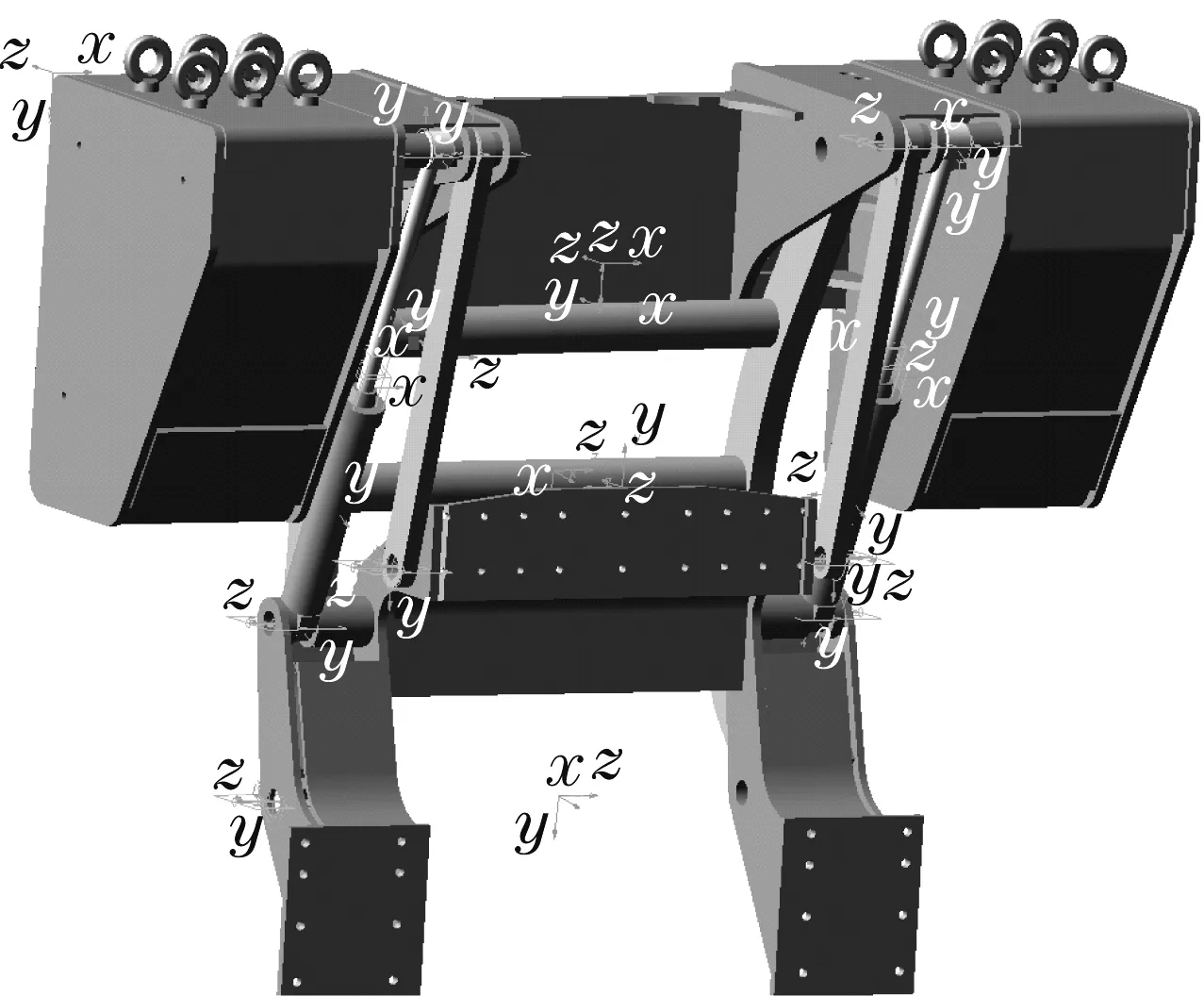
图1 导入Adams中的配重机构模型Fig.1 Counterweight mechanism model imported into Adams
2 配重机构的运动学和动力学仿真
2.1 配重机构运动锁止位置的确定
对配重机构的运动设想是:液压缸收缩时,配重架带着配重块绕连杆和外摆架的下支点旋转,实现配重机构的外摆;液压缸伸出时,配重机构收回。
定义2 个Measure,分别测量配重机构的质心在y向(外摆方向)的位移和液压缸的长度变化。设定仿真时间为60 s、步数为500步,采用默认的求解器、积分方法和误差设置,进行仿真。仿真进行53.4 s后,发生错误而自动停止,说明在这个位置发生运动干涉,是配重机构外摆的极限位置。
2.2 配重机构的运动学和动力学仿真
为了更加准确地描述液压缸的动作,用Step函数Step(time,0,0,53,-530),代替之前的液压缸移动副的驱动。
对自重达到12.5 t 的配重机构来说,其承重部件和液压缸的受力也是需要考虑的重要参数。为此,在Adams 中又建立了3 个measure:连杆的受力F1、外摆架的受力F2、液压缸的驱动力F3(配重机构的展开和收回是对称的,这里只考虑展开过程)。
3 吊管机配重机构的结构优化
仿真证明,设计的配重机构达到了提供一定平衡力矩的要求,也得到了涉及可靠性的承重部件和液压缸的受力等关键参数[5]。为进一步对初步设计的配重机构进行完善,使其达到更好的性能,有必要对其进行结构优化。
3.1 参数化模型的建立
在任何软件环境下,优化的实现都以参数化模型为前提[6]。为实现对配重机构进行优化的目的,需要在Adams 中重新建立参数化模型[7]。把液压缸的移动副驱动设为与之前模型一样的-10×time进行仿真,发现仿真进行至53.4 s 时发生干涉而停止,配重机构的质心沿Y向外移了1 814 mm,说明重建的模型正确。
会计盈余是上市公司盈余披露的一项重要指标,而稳健性是衡量会计盈余质量的最基本特征。通常债权人为了减少损失,会要求更好的会计稳健性;再者,供应商和客户也希望公司能够有效识别经营风险,从而制定相应的应对策略,保障会计稳健性。一方面,会计稳健性的研究有助于帮助人们认识会计稳健性及相关会计行为带来的经济后果,有助于会计信息真实性的判断,进而帮助完善会计准则,保证会计信息披露的真实性。另一方面,会计稳健性的提高有助于优化公司内部管理结构,促进证券市场正常运行,内部控制评价的研究能对建立内部控制体系提供一定的指导。
3.2 优化要素的确定
优化设计就是在满足规定的约束条件的许多可行设计中,以目标函数为标准,找出这个函数的极值(极大或极小),从而选出最优设计方案,它包括目标函数、约束条件和设计变量3个要素[8]。
3.2.1 设计变量的确定
对配重机构而言,任一铰接点位置的改变或任一构件尺寸的变化,都可能影响到配重机构的受力、液压缸行程、质心位移等性能。以配重机构5个关键铰接点坐标作为设计变量,即一共需要设置10 个设计变量,其中,DV_1、DV_2 分别是Point_2(即连杆下端与台车架铰接位置)的Y坐标和Z坐标,DV_3、DV_4 分别是Point_3(即连杆上端与配重架铰接位置)的Y坐标和Z坐标,DV_5、DV_6 分别是Point_4(即外摆架上端与配重架铰接位置)的Y坐标和Z坐标,DV_7、DV_8 分别是Point_6(即液压缸与台车架铰接位置)的Y坐标和Z坐标,DV_9、DV_10 分别是Point_9(即油缸活塞杆与配重架铰接位置)的Y坐标和Z坐标。
3.2.2 目标函数的确定
目标函数是衡量设计方案优劣的某一个或某几个指标。多目标优化问题,各个目标之间往往是相互矛盾的,一般不存在绝对最优解。在这些相互矛盾的目标中寻求一个最优解,实际上是权衡和决策的问题,求得的是权衡基础上的满意解[9]。
影响配重机构性能的因素很多,吸取其他规格吊管机常出现的液压缸损坏的教训,以液压缸受到的最大力最小作为目标函数,优化目标函数可以为
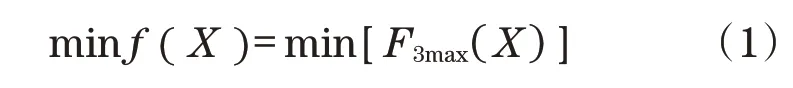
式中:F3max为配重机构展开过程中液压缸受力的最大值;X为选定的设计变量。
3.2.3 约束条件的确定
对配重机构进行参数优化时,需要考虑多方面的约束,包括边界约束、功能约束、初始举升力约束和性能约束等。
(1)边界约束。边界约束,即设计变量的上下限。综合考虑台车架的总体尺寸和配重机构的具体布置,给出了各变量的边界约束如表1所示。

表1 设计变量的边界约束Tab.1 Boundary constraints of design variables
(2)功能约束。为了实现配重机构提供一定平衡力矩的功能,配重机构的质心沿Y向的位移,不得小于1 600 mm。为此,在Adams 中创建一个传感器,当配重机构的质心沿Y向的位移大于或等于1 600 mm时,系统将自动终止仿真。
(3)初始举升力约束。在液压缸外摆的初始时刻,配重机构各铰接点的静摩擦阻力矩最大。为了保证机构外摆时启动平稳,液压缸的最大受力不应出现在配重机构外摆的初始时刻[10],即液压缸的初始举升力F30应小于最大举升力F3max。该约束条件为

式中:η=0.9,通常0.7≤η≤0.9。
(4)传动角约束。在机构运动过程中,传动角的大小是变化的。为了满足机构传动良好,通常应使最小传动角不小于30°[11]。这里用IF函数实现传动角的测量。
用IF 函数建立的某个传动角的表达式是:IF(MEA_ANGLE_19-90:MEA_ANGLE_19,MEA_ANGLE_19,180-MEA_ANGLE_19)。
3.3 配重机构的设计研究
为了对配重机构进行优化设计,把5 个关键铰接点的坐标作为设计变量,即一共设置了10 个设计变量。但这10 个设计变量对目标函数的影响程度有可能不同。如果同时考虑10 个设计变量,势必造成迭代次数的增加和对计算机资源的浪费。为此,可以在正式的优化设计之前,先对配重机构进行设计研究。
首先对DV_1 进行设计研究,将研究对象设置成液压驱动力的最大值,分析模式选择Design Study,设计变量设置为DV_1,在DV_1的取值范围内,设置了5 个试验步。各选项设置好之后,点击右下角的Start,系统自动进行设计研究,并最终得到了图2、图3 所示的变化曲线。从图2、图3 中可以看出,并不是在所有的实验步下质心外摆都达到了要求。从设计研究报告中可以看出:当DV_1 取值-141 时,液压缸所受的最大力最大,为217 024 N;当DV_1 取值-211 时,液压缸所受的最大力最小,为82 060.7 N。DV_1 取初始值-271 时,液压驱动力的最大值是87 346 N,此时,DV_1 对目标函数的敏感度为-81.531。

图2 各实验步质心外摆情况Fig.2 Outward pendulum of center of mass in each experiment step

图3 液压驱动力在各实验步的曲线Fig.3 Curves of hydraulic driving force in each experiment step
按照同样的方法,依次对其他变量进行设计研究,得出设计变量DV_3、DV_4、DV_5、DV_7和DV_8的敏感度最高,也就是说,Point_3的Y坐标和Z坐标、Poing_4的Y坐标、Poing_6的Y坐标和Z坐标的变化对液压驱动力的最大值影响最大。
3.4 配重机构的优化设计
通过对各变量进行设计研究,发现其中5 个设计变量对液压缸的最大驱动力的敏感度最高。下面将以这5 个变量为最终的设计变量,对配重机构进行优化设计。研究的对象依然是液压驱动力的最大值,分析模式选择Optimization,设计变量选择对目标函数敏感度最高的5 个变量:DV_3、DV_4、DV_5、DV_7 和DV_8,优化目标是使液压驱动力的最大值最小,约束条件选择之前建立的传动角约束和初始举升力约束(边界约束已在定义设计变量时定义过、功能约束通过一个传感器实现)。选用数学规划法中的二次规划法作为优化方法。收敛误差限、迭代次数和差分方式等参数采用默认值。
各参数设置好之后,点击Start 按钮,系统将自动进行优化。优化过程中,可以实时观测液压驱动力的变化和液压驱动力最大值随迭代次数的变化,如图4、图5所示。

图4 液压驱动力的变化曲线Fig.4 Variation curve of hydraulic driving force

图5 液压驱动力最大值的变化曲线Fig.5 Change curve of maximum hydraulic driving force
4 优化结果分析
将优化的结果代入,重新进行仿真,得到了优化之后各性能参数的曲线,如图6~图8 所示。从图6 中可以看出,优化之后,液压缸驱动力的最大值为65 531 N,较优化之前下降了24.9%。驱动力的最大值也不再出现在初始仿真位置,从而使配重机构的启动更加平稳。优化之后,质心外摆至指定位置所用的时间(仿真结束的时间)为39.4 s,较仿真之前的39.3 s 变化不大,即在使液压缸驱动力最大值大幅度减小的同时,机构的运动效率并没有受到影响。从图7、图8 中可以看出,在配重机构整个外摆过程中,2 个传动角始终大于30°,从而保证了机构有较高的传动质量。

图6 优化前后液压驱动力的变化曲线Fig.6 Change curve of hydraulic driving force before and after optimization

图7 优化前后传动角1的变化曲线Fig.7 Change curve of transmission Angle 1 before and after optimization
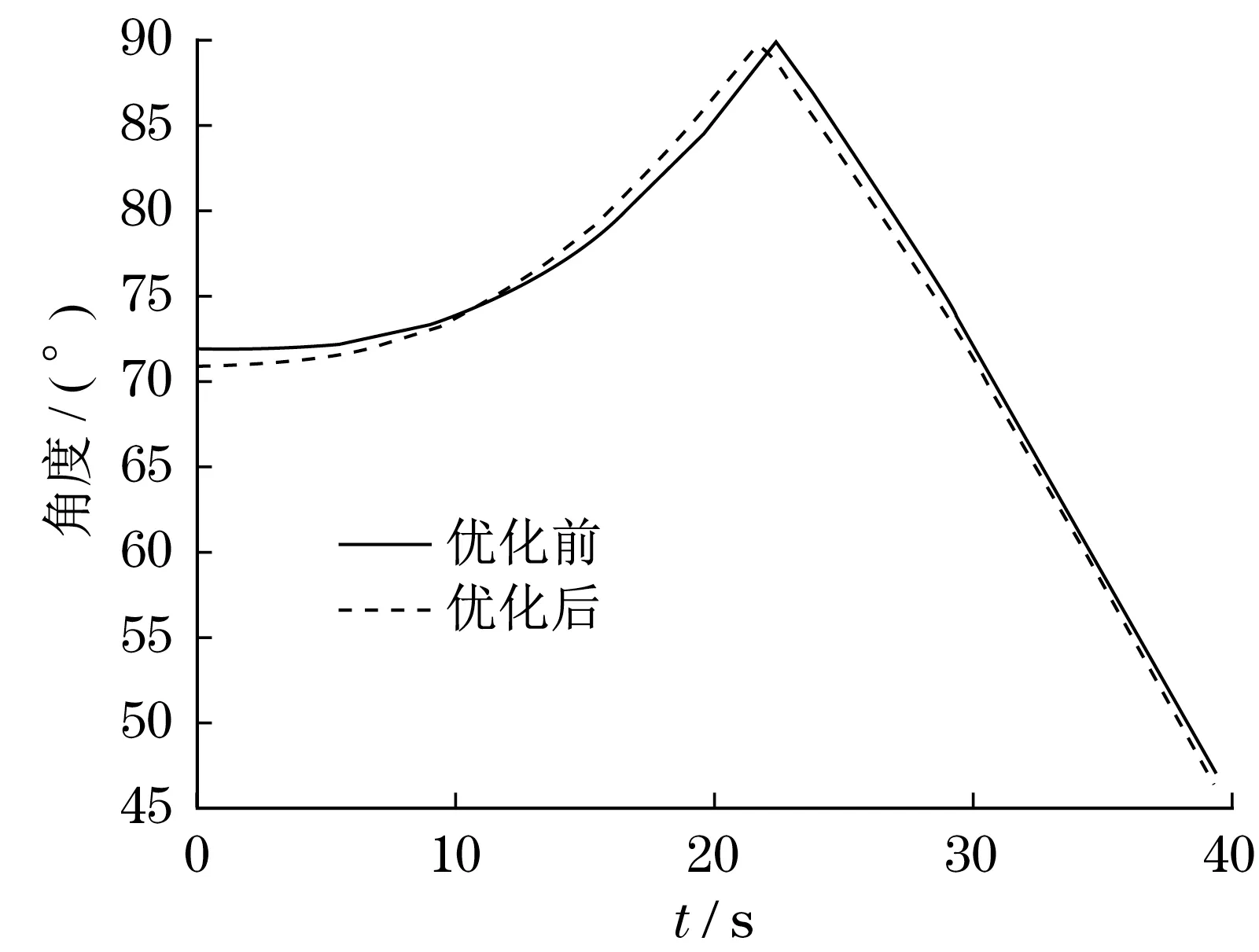
图8 优化前后传动角2的变化曲线Fig.8 Change curve of transmission Angle 2 before and after optimization
通过以上对各性能曲线的分析知道,在保证配重机构的基本功能不变的前提下,通过改变几个关键铰接点的坐标位置,大幅度减小了液压缸的受力,同时还实现了机构的平稳启动,使其具有了更高的传动效率和传动质量,达到了优化设计的目的。
5 结语
在Adams 中,对所设计的配重机构进行了运动学和动力学仿真,得到了质心沿Y向位移、连杆、外摆架和液压缸的受力等关键参数;为验证虚拟样机技术得到的各参数的正确性,对模型进行了简化,用解析法对以上参数进行了计算,利用Matlab编写了计算程序,计算结果证实了各参数的正确性及虚拟样机技术的可靠性;在Adams 中重新建立了配重机构的参数化模型,对10 个设计变量进行了设计研究,得到了对液压驱动力敏感度最高的5个参数;以这5 个参数为设计变量,以液压驱动力最大值最小为目标函数,对所设计的配重机构进行了结构优化,减小了液压缸的受力,并使其具有了更高的传动效率和传动质量。

