冗余液压机械手双伺服阀驱动控制仿真研究

谢祥洲，陈小兵，张 潞

（1.电子科技大学自动化工程学院，四川成都 611731；2.重庆城市管理职业学院智能工程学院，重庆 401331；3.广东开放大学人工智能学院，广东广州 510091）

当今世界，智能制造逐步替代了传统制造方法，已经成为各国发展制造业的重要举措。为了加快经济发展，实现制造大国向制造强国的转变，必须发展智能化技术，工业机械手是反映一个国家智能化生产的重要标志。机械手具有加工精度高、可以连续工作、承载能力强等优点，其应用范围也在逐步扩大，广泛应用于医疗、海洋、工业和航空等许多领域［1］。近些年，我国已经成为全球机械手最大消费市场之一。机械手涉及机械、数学、电子、通信及人工智能等多种交叉学科，研究起来相对复杂。与国外机械手相比，关键技术还存在一定的差距。机械手加工精度要求越来越高，每个环节设计都很重要，若设计不当，就会导致机械手无法按照指定轨迹运动，这对当前机械手研究人员提出了新的挑战。为了提高机械手运动精度，刘侃等［2-3］采用遗传算法优化机械手运动路径，得出机械手运动路径最优参数，有效地缩短了机械手运动时间。郭永凤等［4-5］采用遗传算法优化PID控制器，提高了液压机械手末端执行器的响应速度。张传胜等［6-7］利用外力对机械手运动产生的抖动进行补偿，能够降低液压机械手抖动幅度。菅光霄等［8-9］提出自适应滑模控制方法，利用神经网络对控制参数进行逼近，具有较好的响应速度和控制精度。上述方法主要是针对冗余液压机械手控制系统进行设计，很少对伺服阀驱动系统进行改进。随着伺服阀应用的日益增多，现有的伺服阀驱动系统很难再适应市场的快速发展，需要一套对应的伺服阀改进系统。双伺服阀驱动系统能够显著改善冗余液压机械手的控制精度和能量消耗。

1 伺服阀驱动

1.1 伺服阀控制

目前，电液伺服阀控制是液压执行机构在控制精度和响应时间方面进行高精度控制的必要条件。液压机械手采用传统的伺服阀控制，如图1所示。

图1 单伺服阀驱动Fig.1 Single servo valve drive

在这种伺服阀控制中，液压缸活塞杆推力fp可以写成

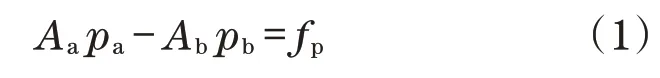
式中：Aa、Ab分别为无杆腔和有杆腔活塞的面积；pa、pb分别为无杆腔和有杆腔的压力。

采用单独的仪表输入和输出对传统伺服阀控制进行改进，如图2 所示。仪表输入和输出孔之间的机械连接被移除，每个气缸室由单独的伺服阀控制，使腔室压力pa和pb可控。这种改进可以降低液压执行机构的能源消耗，也能够提高腔室压力的跟踪精度。

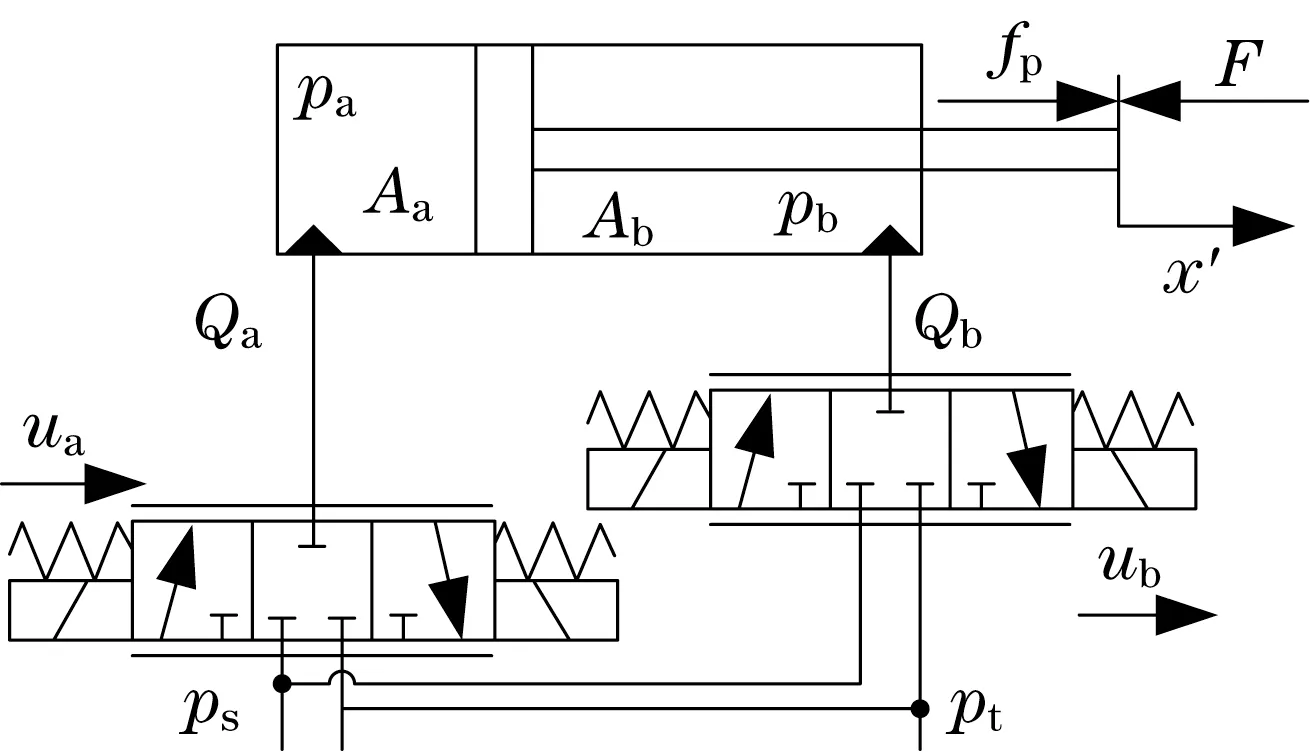
图2 双伺服阀驱动Fig.2 Dual servo valve drive

液压能源消耗方程式［10］可定义为

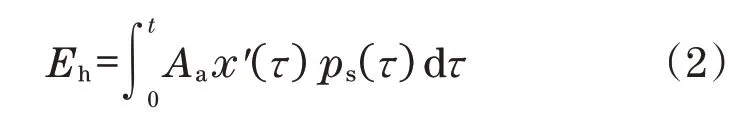
式中：ps（τ）为供给压力；x′（τ）为活塞移动速度。

在传统的伺服阀控制中，供给压力定义为

单独仪表输入和输出控制的腔室供给压力可以定义为

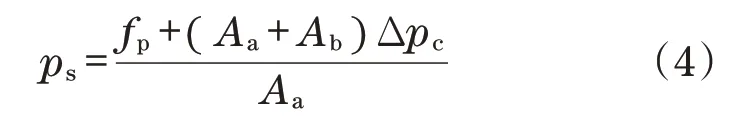
1.2 能量消耗优化

令活塞杆推力fp为已知一个光滑可微函数，腔室压力pa和pb必须满足式（1）。为了避免腔室中产生气穴，对于任意时段t，pa（t）≥Δpc，pb（t）≥Δpc，Δpc＞0。为了使腔室压力降到最低，Δpc必须保持至少一个腔室压力值，即

根据限制条件，压力值定义为

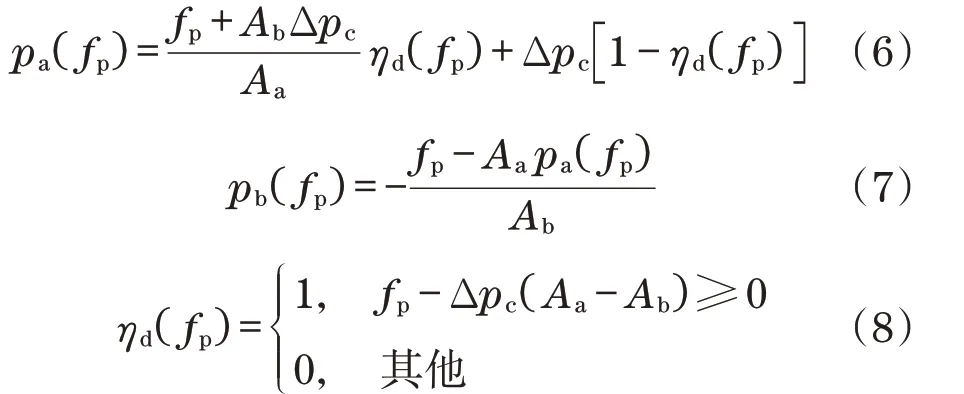
如果在控制设计中需要时间导数和，则由于开关函数不连续（不可微），不能使用式（6）和式（7）中设计的压力值。因此，平滑（连续可微）开关函数修改为

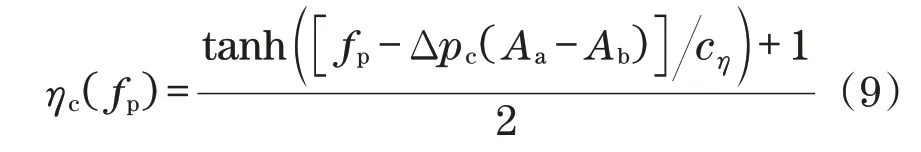
式中：cη＞0为足够小的常数。

可微腔室压力值修改为

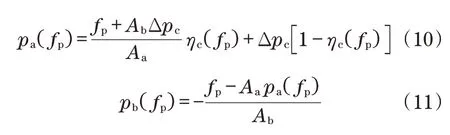
2 冗余机械手控制器设计

2.1 冗余液压机械手

冗余液压机械手如图3 所示，液压缸通过双伺服阀驱动，完成末端执行器伸长与缩短任务。

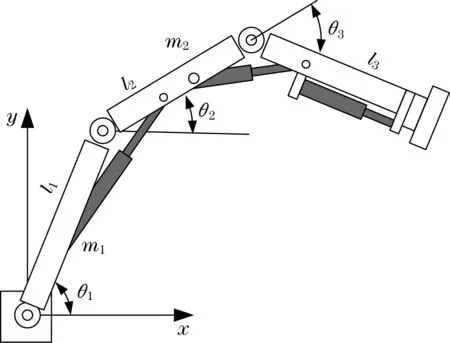
图3 冗余液压机械手Fig.3 Redundant hydraulic manipulator

在平面坐标系中，冗余液压机械手末端执行器位置关系式为

式中：xw、yw分别为末端执行器横向、纵向坐标位置；l1、l2、l3分别为机械手连杆1、连杆2 和连杆3 的长度；θ1、θ2、θ3分别为连杆1、连杆2 和连杆3 与横向之间夹角。

采用双伺服阀驱动冗余机械手运动，使末端执行器能够按照期望轨迹运动。但是，在实际运动过程中，不可避免产生误差，其误差定义为

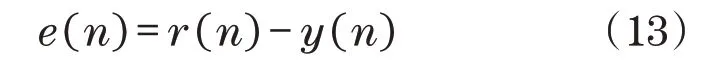
式中：r（n）为期望运动轨迹；y（n）为实际运动轨迹。

2.2 控制器设计

增量式PID 控制器是目前较为常见的一种控制系统，其控制方程式［11-12］为

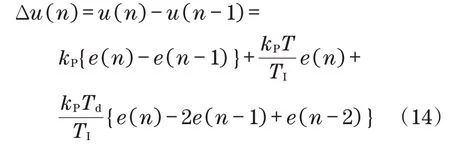
式中：kP、kI、kD分别为比例、积分和微分调节系数；TI、TD分别为积分和微分时间常数；T为采样周期。

为了提高增量式PID 控制器输出精度，采用粒子群算法（particle swarm optimization，PSO）对PID 控制器调节系数进行优化。通过更新粒子的位置和速度来搜索全局最优值，其位置和速度方程式［13-14］定义为

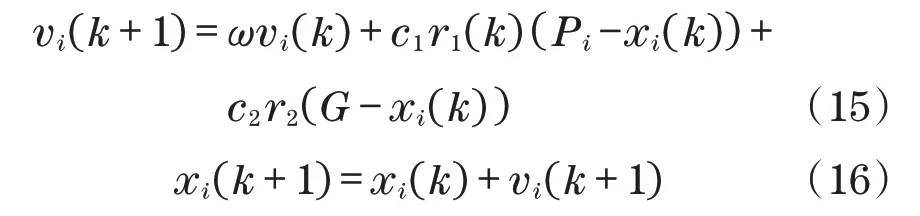
式中：vi（k+1）为粒子i更新（k+1）次的速度；vi（k）为粒子i更新k次的速度；xi（k+1）为粒子i更新（k+1）次的位置；xi（k）为粒子i更新k次的位置；ω为惯性权重系数；c1和c2为区间［0，2］之间的学习速率参数；r1和r2为区间［0，1］之间的随机参数；Pi和G分别为粒子局部和全局最优位置。

惯性权重系数直接影响到粒子最优位置的搜索能力，为了提高PSO 的优化能力，对惯性权重系数进行修改：

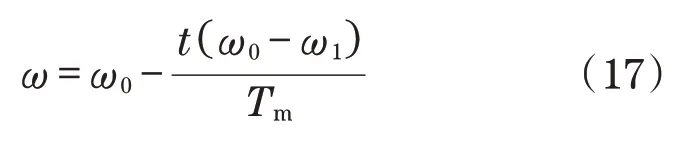
式中：t为粒子目前更新次数；Tm为粒子更新最大次数；ω0为更新开始权重系数；ω1为更新最后权重系数。

采用PSO 对冗余液压机械手增量式PID 控制器进行优化，其优化控制流程如图4所示。

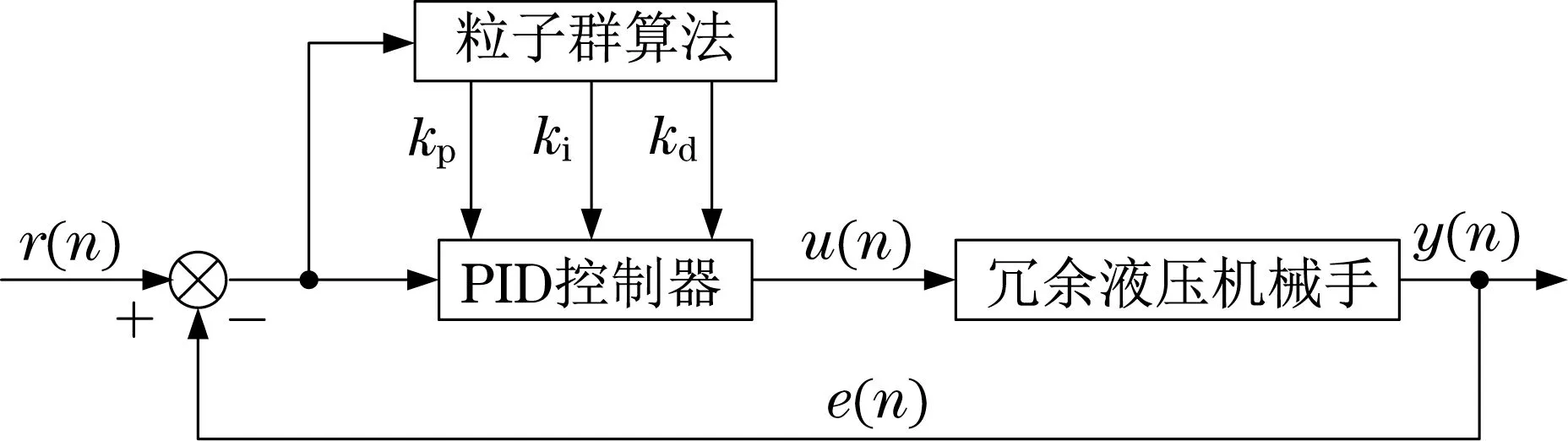
图4 冗余液压机械手控制优化流程Fig.4 Control optimization process of redundant hydraulic manipulator

3 对比和分析

为了对比单伺服阀驱动与双伺服阀驱动冗余液压机械手输出效果，采用Matalb 软件对其进行仿真。通过仿真验证冗余机械手末端执行器跟踪误差和能量消耗，并且对仿真结果进行分析和说明，假设仿真参数设置为：种群大小为100，粒子更新最大次数Tm=500，开始权重系数ω0=0.9，最后权重系数ω1=0.1，学习速率参数c1=c2=2.0，随机参数r1=r2=1.0，连杆长度l1=l2=l3=0.4 m，连杆质量m1=m2=m3=0.2 kg，仿真时间为4 s。

假设冗余液压机械手末端执行器期望运动轨迹由改进正弦和节约波形组合。采用单伺服阀驱动冗余液压机械手，其末端执行器跟踪误差如图5所示。采用双伺服阀驱动冗余液压机械手，其末端执行器跟踪误差如图6 所示。2 种伺服阀驱动能量消耗如图7所示。

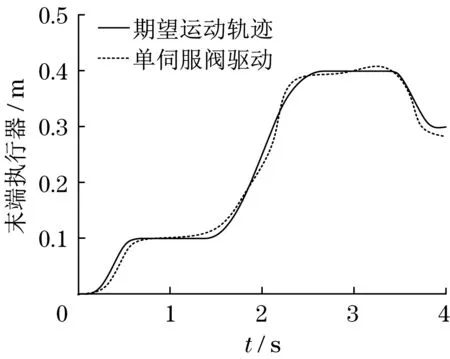
图5 单伺服驱动跟踪误差Fig.5 Single servo drive tracking error

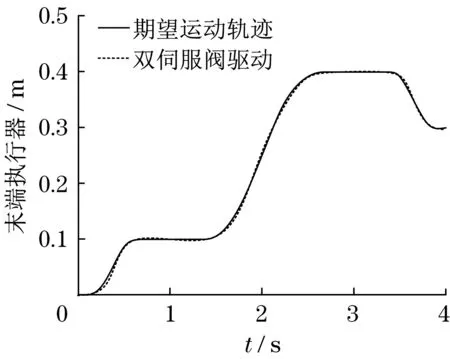
图6 双伺服阀驱动跟踪误差Fig.6 Double servo valve drive tracking error

图7 能量消耗Fig.7 Energy consumption

由图5 和图7 可知，采用单伺服阀驱动冗余液压机械手，其末端执行器实际运动轨迹与期望值偏差较大，导致其消耗的能量较多。由图6 和图7 可知，采用双伺服阀驱动冗余液压机械手，其末端执行器实际运动轨迹与期望值偏差较小，导致其消耗的能量较少。采用双伺服阀驱动冗余液压机械手，避免了腔室两端压力相互干扰，通过改进PID 控制器对腔室压力进行自适应调整，不会造成负载力的额外增加，使冗余液压机械手末端执行器与期望运动轨迹偏离程度较小。不仅能提高其运动轨迹跟踪精度，而且还节约了能量消耗，效果较好。

4 结语

由于冗余液压机械手末端执行器运动轨迹偏离误差较大，导致能量消耗相对严重，设计了双伺服阀驱动系统，并且采用改进PID 控制器，通过仿真验证单伺服阀和双伺服阀驱动系统输出效果。采用双伺服阀驱动冗余液压机械手明显优于单伺服阀，其末端执行器运动轨迹偏离误差较小，能量消耗相对较少，效果较好。同时表明，利用PSO 优化增量式PID 控制器参数，其目的是搜索到最优PID 控制器调节系数，使PID 控制器能够较好地控制冗余液压机械臂腔室压力。利用Matlab 软件对冗余液压机械手末端制器跟踪精度和能量消耗进行仿真，能够检测双伺服阀驱动系统的优越性，进一步验证双伺服阀驱动冗余液压机械手的优越性，可以帮助设计者更好地改进和优化。