基于遗传算法的钢拱架安装机作业平台调平系统优化设计

赵 津，黄信念，卢 静，张家放

（1.贵州大学机械工程学院，贵州贵阳 550025；2.贵州大学现代制造技术教育部重点实验室，贵州贵阳，550025；3.中铁五局集团贵州工程有限公司科技部，贵州贵阳 550003）

钢拱架安装机是一种应用于道路隧道建设过程中对软弱围岩安装支护的工程车辆，具有高效、准确、方便、降低劳动强度等优点，可有效提升我国隧道施工机械化水平［1］。某型钢拱架安装机采用两臂一篮轮胎式设计（见图1），施工时其作业平台需举升工人至合适位置进行螺栓安装，因此，调平系统须保证作业平台在举升及下降过程中始终保持水平，否则可能导致安全事故。对于静液压调平系统，影响调平精度的最主要因素是油缸的尺寸和铰点位置，同时，铰点的布置直接影响着油缸的负载值和压力冲击［2］。因此，优化设计油缸尺寸和铰点位置，达到理想调平效果及力学性能，对保障施工人员安全具有重要意义。

图1 某型钢拱架安装机Fig.1 A type of steel arch installation vehicle

针对此类结构优化设计问题，Diab 等［3］基于蚁群算法提出了一种平面机构“精确-近似”尺寸合成的优化方法。Kim等［4］以提高效率和减小径向力为目标函数，利用第二代非劣排序遗传算法（NSGA-Ⅱ）与代理模型相结合，对某单通道水泵结构进行了优化。赵克利等［5］针对车载高空制瓦设备折叠举升机构，以降低液压缸工作压力和提高其油压稳定性为优化目标，采用遗传算法对液压缸铰点位置进行了优化求解，并通过ADAMS 进行了仿真验证。骆清国等［6］应用计算流体力学与遗传算法相结合的方法，以空气流动阻力最小为目标，以蜗壳几何尺寸为约束条件，对履带车辆动力舱冷却风道的风扇蜗壳进行了结构优化。王琪等［7］针对双层剪叉式液压升降台，基于粒子群算法，以液压缸铰点位置参数为设计变量，活塞推力及起升速度为目标进行多目标优化。周友行等［8］提出了一种改进型黄金分割轮换法对调平系统液压缸组的铰点位置进行了优化设计。占自涛等［9］以降低最大工作压力与提高压力稳定性为目标，采用遗传基因算法对铁钻工铰接臂铰点位置进行了优化设计，并通过ADAMS 进行了动力学仿真分析，对算法的优化效果进行了验证。

本文针对钢拱架安装机作业平台调平系统建立数学模型，利用遗传算法对油缸铰点位置进行优化计算，通过对比优化前后调平系统的误差及受力情况，验证优化效果，实现对作业平台工作性能的提升。

1 调平系统结构、原理及受力分析

本钢拱架安装机作业平台调平系统采用静液压调平结构，主要由回转底座、变幅油缸、主动调平油缸、臂架、作业平台、从动调平油缸组成（见图2）。主动调平油缸连接在回转底座和臂架之间，从动调平油缸连接臂架和作业平台，2个调平液压缸的无杆腔与无杆腔相连，有杆腔和有杆腔相连，组成1个封闭的液压系统，且通过补油平衡装置保证长期使用后的调平精度。当主动调平油缸在变幅油缸的带动下做伸缩运动时，从动调平油缸做相反的缩短伸长运动，让平台转动的角度与臂架转过的角度相等，作业平台始终处于水平状态，从而实现调平。

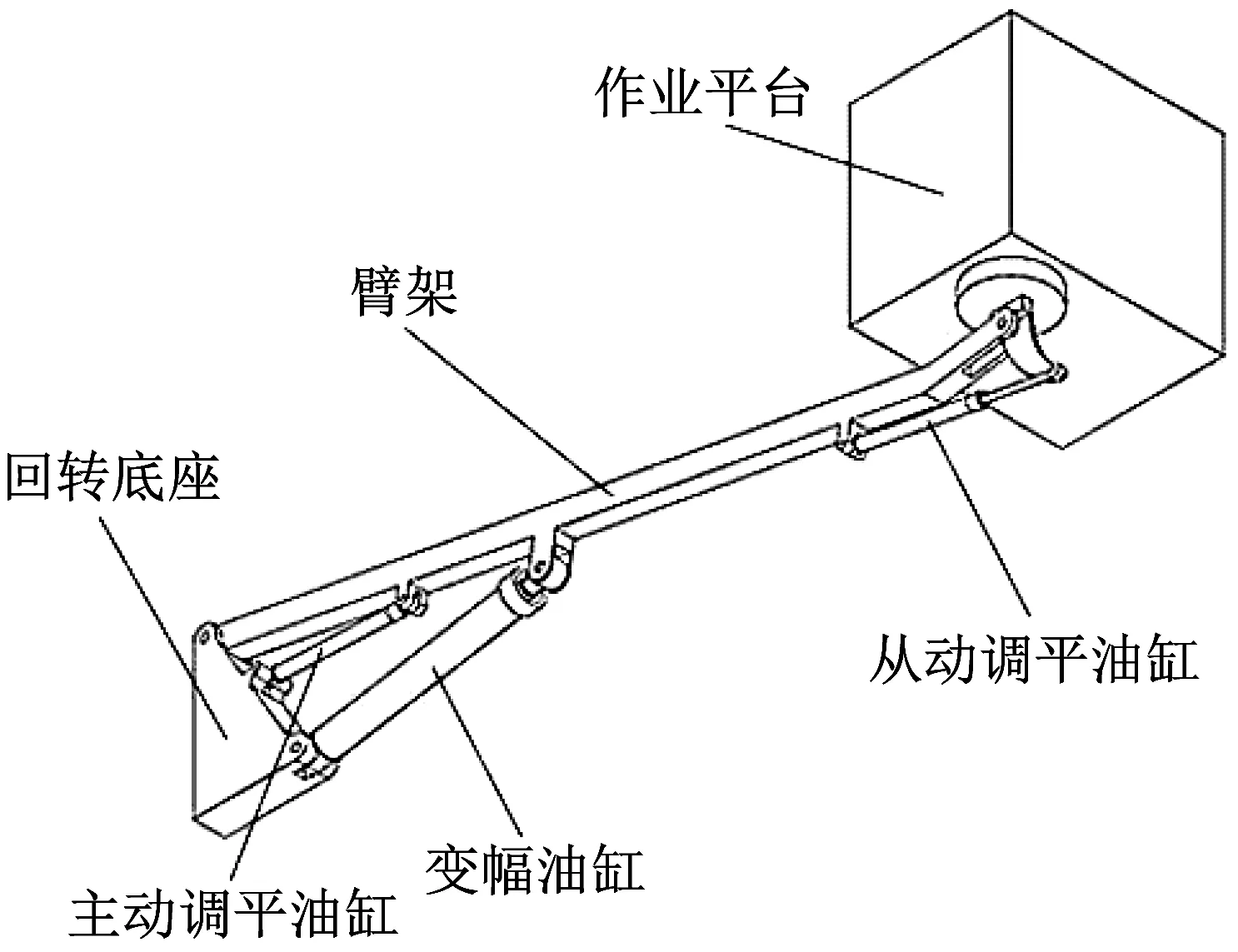
图2 作业平台结构Fig.2 The structure of work platform

由上述结构分析及调平原理可知：从动调平油缸作为作业平台的驱动件，除需保证调平精度外，还需保证其力学性能，使得油缸受力较小；而下调平系统有变幅油缸作为受力主体，故无需考虑主动调平油缸受力情况。

静液压调平系统如图3 所示。图中：A1为臂架与底座的铰点；B1为主动调平油缸与底座的铰点；C1、为主动调平油缸的初状态和末状态铰点位置；A2为臂架与作业平台铰点；B2为从动调平油缸与臂架铰点；C2、为从动调平油缸的初状态和末状态铰点位置。

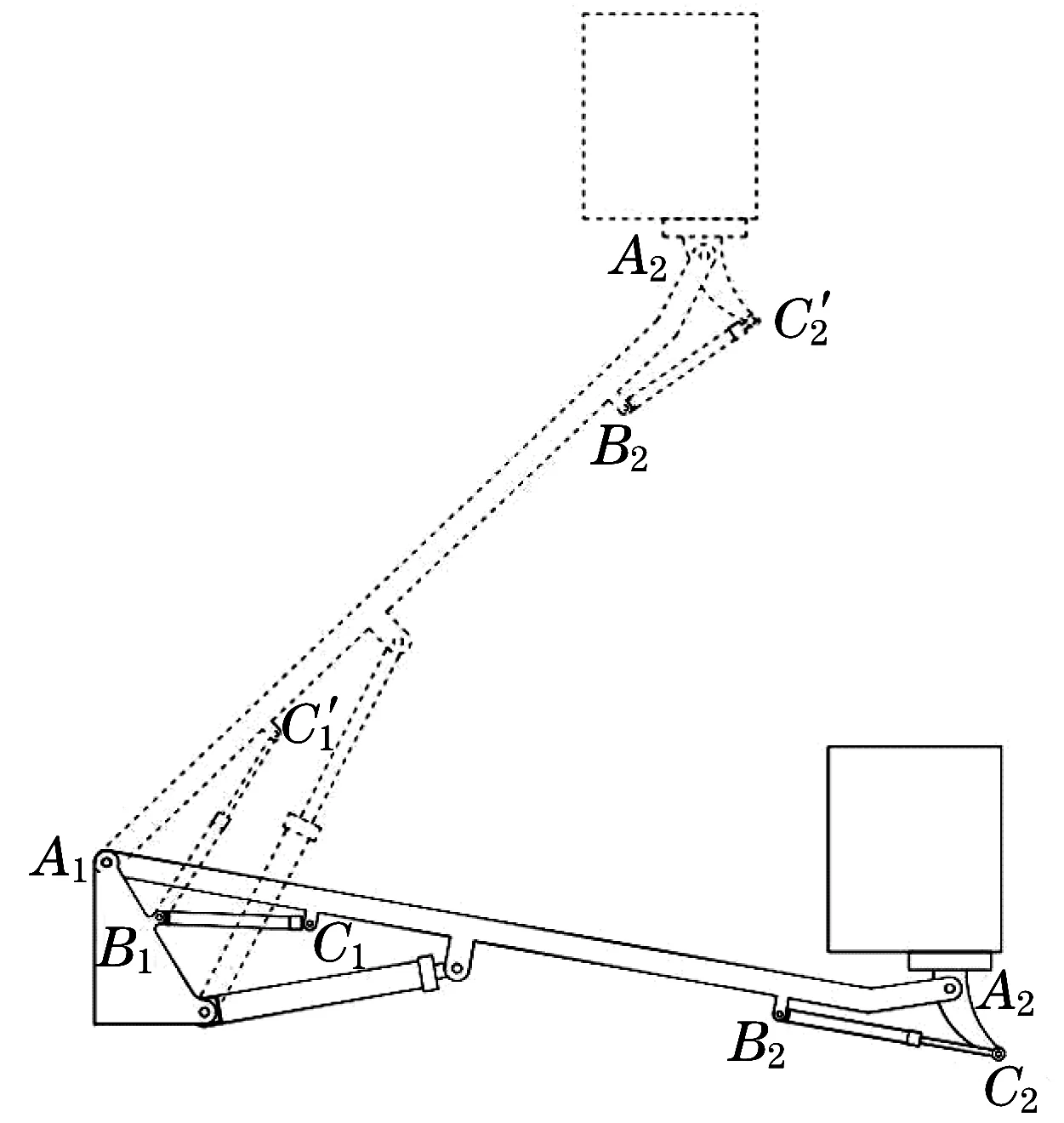
图3 静液压调平系统Fig.3 Hydrostatic leveling system

由于选用相同型号的主动调平油缸与从动调平油缸，根据油缸流量相等原理，则主动油缸伸长量等于从动调平油缸缩短量，故当变幅角度为θ时，从动调平油缸长度L'5为

则工作平台转过的角度为

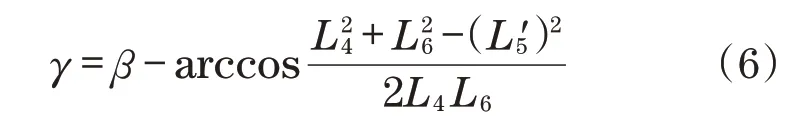
故可得调平误差为

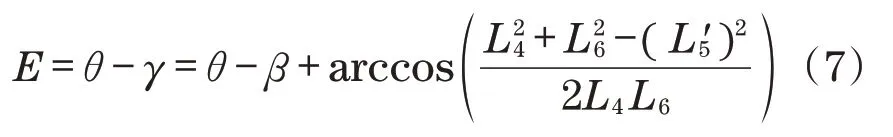
设F为从动调平油缸受力，L为从动调平油缸对铰点A2的力臂，M为调平油缸所受力矩，当作业平台按额定质量负载时有M=800.17 N·m，公式如下：

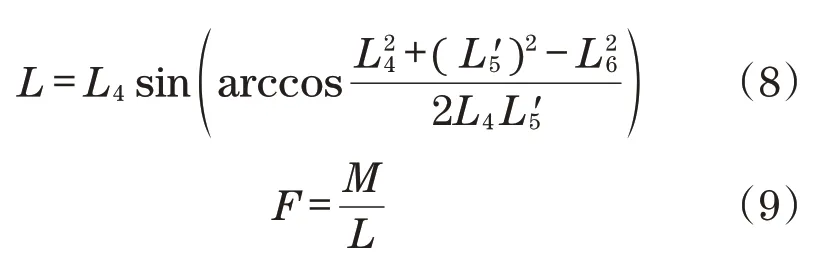
由式（7）可知，调平误差是一个多变量非线性复杂函数，由调平过程中2 个三角形边长和角度共同影响。根据我国《高空作业机械安全规则》［10］规定，平台台面与水平面的夹角不得超过1.5°。

2 优化模型

根据机械最优化设计理论［11］，作业平台调平系统油缸铰点位置的优化设计可抽象为非线性多目标、多约束规划问题，其数学模型为

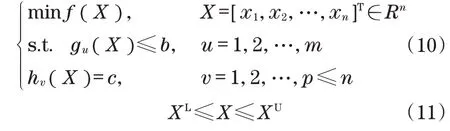
式中：X为n维设计变量；f(X)为目标函数；gu（X）为不等式约束；hv（X）为等式约束；m、p分别为不等式约束和等式约束的数目；XU和XL分别为设计变量的上、下限。

2.1 目标函数

结构调平误差、调平油缸受力是影响调平系统性能和作业平台安全最关键的2 个因素，因此本文以调平误差和从动调平油缸受力最小为优化目标函数，并利用线性加权和法对双目标优化问题构造评价函数，形成统一目标函数。

2.1.1 调平误差目标函数

钢拱架安装机作业平台作为载人平台，须保证在变幅臂运动过程中，始终保持水平状态，故以调平误差作为子目标函数，结合式（7），并以Matlab匹配形式表示为

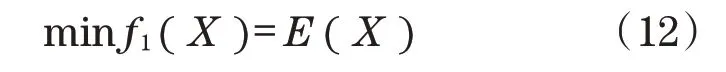
2.1.2 从动调平油缸受力目标函数

从动调平油缸在对作业平台的调平过程中，不仅应保证调平精度，也要兼顾油缸受力应最小。结合式（8）和式（9），子目标函数可表示为

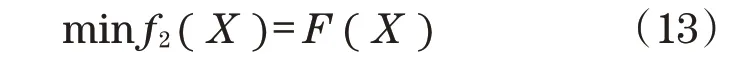
2.1.3 统一目标函数

确定上述2 个子目标函数后，采用线性加权和法将双目标函数优化问题转化为单目标函数优化问题，即根据各子目标函数的重要程度给予权重系数，并分别与对应的子目标函数相乘后相加，组成一个新的统一目标函数，表达式为

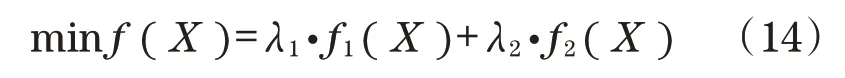
权重系数应满足归一性和非负性条件为

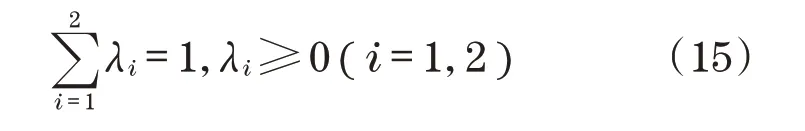
分别对子目标函数进行无量纲处理［11］如下：

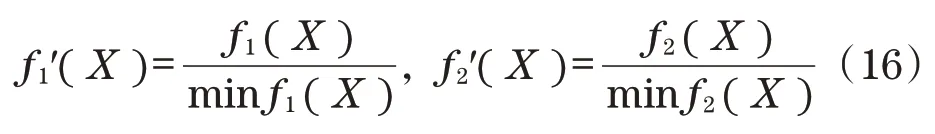
依据调平误差和油缸受力2 个子目标函数对调平系统影响的重要程度，并考虑数量级影响，得到最终统一目标函数为

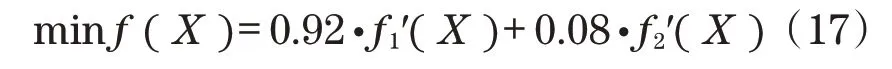
2.2 设计变量

由上述分析可知，对于调平油缸铰点位置的优化问题实质上是确定△A1B1C1和△A2B2C2的6 条边长，由于可利用余弦定理或选用已知参数的油缸型号来确定L2和L5的值，故选取L1、L3、L4、L6为设计变量，表达式为

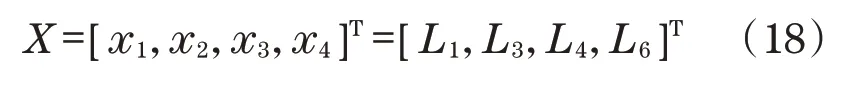
2.3 约束条件

2.3.1 边界条件

根据钢拱架安装机作业平台系统尺寸及各部件布局情况，同时结合各个设计变量的初始值，为了缩小寻优范围，给4 个设计变量设置上、下限，由此建立8个边界约束条件，可统一表示为

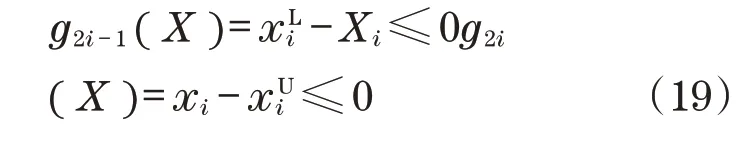
式中：XU和XL分别为设计变量的上、下限，i=1，2，…，6。

2.3.2 油缸伸缩比约束

为了满足油缸的可制造性和运动中的稳定性与可靠性，调平油缸的伸缩比需小于1.7，表达式为

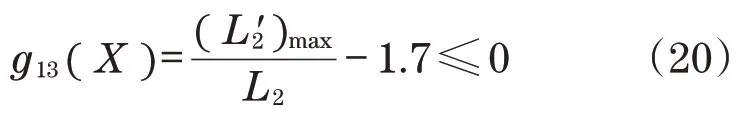
3 优化结果及验证

3.1 优化结果

根据钢拱架安装机工作及尺寸要求，取主动调平油缸初始调平角α=29.56°，从动调平油缸初始调平角β=118.45°，臂架变幅角θ=［0，75°］，选用结构尺寸完全一致的主动和从动调平油缸，行程为880～1 300 mm。在分析了本作业平台调平系统的结构并参考相关成熟设计后，由单个参变量变化及设计经验得出待优化参数的可行解范围，见表1。

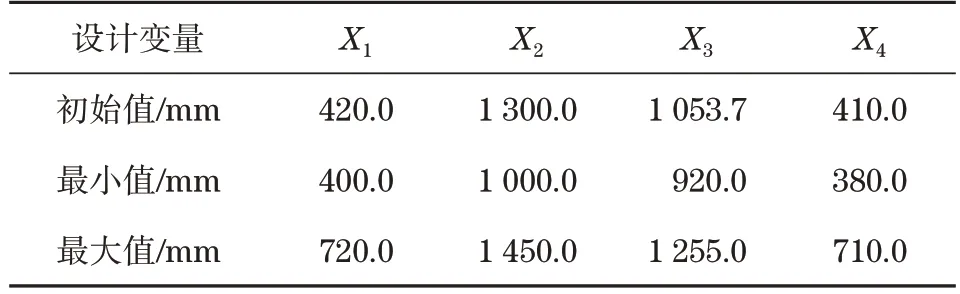
表1 主、从动调平油缸铰点参数及可行域Tab.1 The hinge parameters and feasible region of active leveling cylinder and slave leveling cylinder

选择种群大小M=200，编码方式为格雷码混合编码，选择操作采用轮盘赌转轮法，单点交叉，交叉率Pc=0.6，变异率Pm=0.02，进化代数N=100，α=0.995，繁殖数σ=5，繁殖率μ=0.85［12-13］。通 过Matlab 遗传算法工具箱求解并在几十组数据中对比以后，得到了4 个设计变量的最终优化结果，见表2。

表2 主、从动调平油缸铰点尺寸优化结果Tab.2 The optimized result of hinge size of active leveling cylinder and slave leveling cylinder

因此，得到优化后的最终设计参数为：L1=422.96 mm，L2=800.00 mm，L3=1 222.81 mm，L4=1 038.83 mm，L5=1 300.00 mm，L6=430.18 mm。根据式（1）～式（7），在臂架变幅范围内，优化前后调平误差曲线对比如图4 所示，从动调平油缸受力曲线如图5所示。

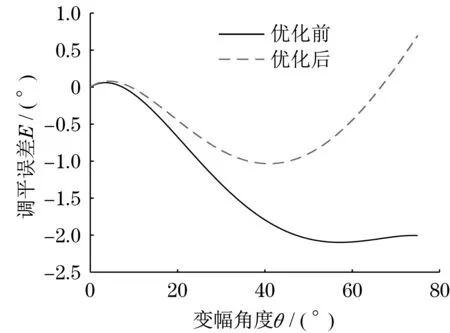
图4 优化前后调平误差曲线对比Fig.4 The leveling error curves comparison between before and after optimization

可以看出，优化后最大误差值从2.097°下降至1.034°，降低了50.69%，且优化后调平误差小于1.5°达到了安全规则要求；从动调平油缸最大受力值从2 738 N 降至2 647 N，降低了3.32%，且整体受力降幅明显。

3.2 测试验证

为验证多目标遗传算法（multi-objective genetic algorithm，MOGA）求解得到的油缸铰点尺寸对于作业平台调平系统优化效果的可靠性，在Pro/E软件中，以优化后的油缸铰点尺寸，建立作业平台的三维模型，导入ADAMS 软件如图6所示，并分别在主、从动调平机构的调平角∠B1A1C1和∠B2A2C2处添加角测量工具，设置完各参数后进行运动学仿真。由调平原理可知，下调平角变化的角度等于上调平角反向变化的角度，即上下调平角之和不变即可实现调平，故将两调平角在作业平台运动过程中角度变化值相加，即可得到调平误差曲线，如图7所示。

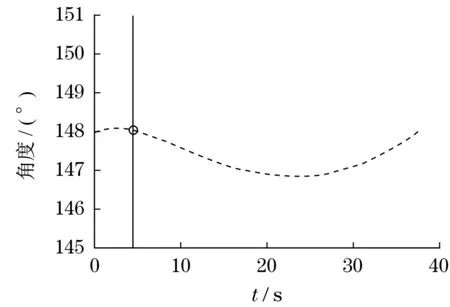
图7 运动学仿真调平误差曲线Fig.7 The leveling error curve from kinematics simulation

由于2 初始调平角α与β之和为148.01°，根据图7 可知，作业平台在整个运动过程中最大调平误差为1.2°，相比2.097°的原始调平误差下降了42.78%，并满足了小于1.5°的行业标准，从而验证了MOGA的优化效果及可靠性。

4 结语

通过对钢拱架安装机作业平台调平系统进行结构分析和受力分析，建立了减少调平误差和从动调平油缸受力的目标函数，并利用Matlab 遗传算法工具箱进行优化，最后通过ADAMS 进行虚拟样机测试验证。对比原始设计，优化后最大调平误差减少至1.034°，降幅为50.69%，从动调平油缸最大受力值减少至2 647 N，降幅3.32%。仿真结果表明，优化后的油缸铰点布置有效提高了作业平台调平系统的调平精准度和力学性能，为类似的机械优化设计问题提供了思路。