具有时滞的HR神经元模型的分岔分析
陈国泰,郑艳红,易 丹,曾巧云
(福建师范大学数学与统计学院,福建福州 350117)
在大多数的物理和生态系统中,时滞是普遍存在的.它主要来源于信号有限的波动速度.由于时滞的出现,使得有限维的动力系统转变为无穷维的动力系统,并且诱导了更为复杂的非线性动力特征[1].此外,在神经元模型中,时滞的存在往往会导致神经模型的平衡点失去原有的稳定性.神经系统是由众多的神经元组成的复杂的生物神经元网络,神经元作为神经系统的基本功能和单位,其活动具有高度的非线性,因此时滞神经模型系统的非线性行为吸引许多学者的关注.目前,通过对神经元的了解,人们已经建立了H-H(Hodgkin,Huxley),HR(Hindmarsh-Rose)和Chay 等神经元模型[2-4],运用这些模型可以精确地模仿神经元的放电活动.近年来,由于HR 神经元形式简单,为了更好地了解信息在大脑的传播,HR神经元模型通常被作为分析现实神经元网络的理想模型.因此,基于以上想法,对HR 神经元模型进行改进,加入时滞,建立新的模型,如
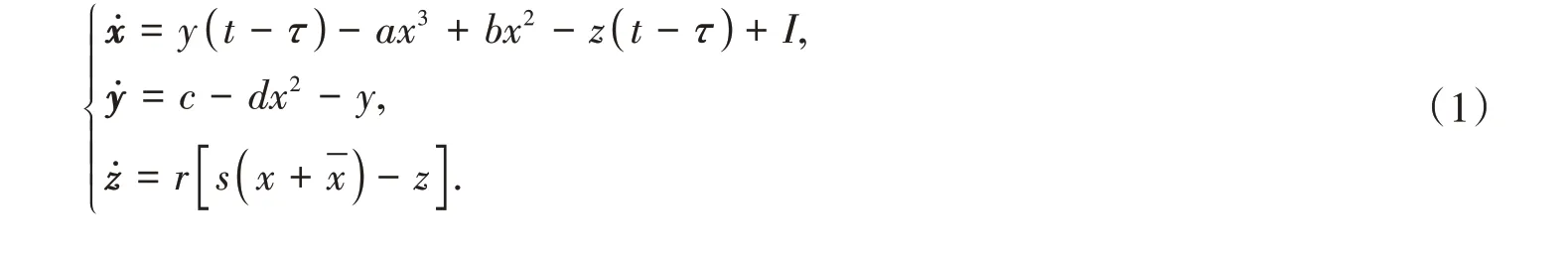
1 正平衡点分析
假设E0(x*,y*,z*)是式(1)在τ=0 的平衡点,令上述时滞微分方程模型右端为0,则x*应该满足下列等式:
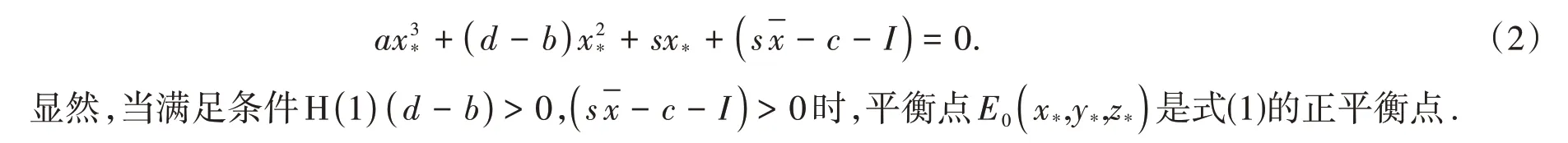
2 Hopf分岔分析
为了进一步分析式(1)在平衡点处Hopf 分岔的存在性,作以下平移变换[5]:,仍用表示x,y,z,那么,式(1)等同于以下系统:

在本节中,考虑两种情形.
情形1τ=0,式(6)变为
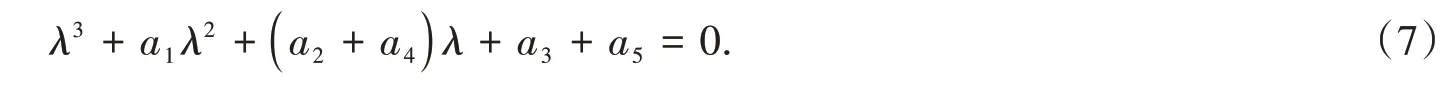
由Routh-Hurwitz 判据[6]可得:
定理1式(1)在平衡点处是渐进稳定的当且仅当式(7)的全部特征根都具有负实部,即式(7)的系统满足条件H(2)a1>0,a1(a2+a4)>(a3+a5)>0.
式(7)的全部特征根都具有负实部,即式(3)在平衡点( 0,0,0)处是局部渐进稳定的,式(1)在E0(x*,y*,z*)处是局部渐进稳定的.
下面考虑时滞系统式(3)在平衡点( 0,0,0)稳定性的影响,由于式(6)的根与τ必然存在联系,因此τ的变化会导致式(6)根的变化,若存在τ的一个临界值,使得式(6)的某个根出现为0 的实部,则在此临界处式(3)在平衡点( 0,0,0)处的稳定性将发生改变,在某些条件下会从平衡点( 0,0,0)处分岔出一簇小振幅的周期解,即在平衡点( 0,0,0)处出现了Hopf分岔[7].
情形2τ>0,则式(3)的特征方程仍为式(6).设式(6)有虚数根,设虚数根为λ=iω(ω>0),将λ=iω代入式(6)可得
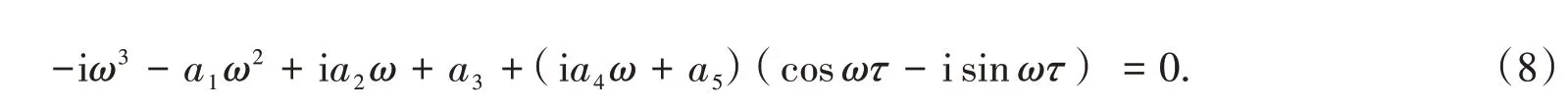
将式(8)分离实部、虚部可得
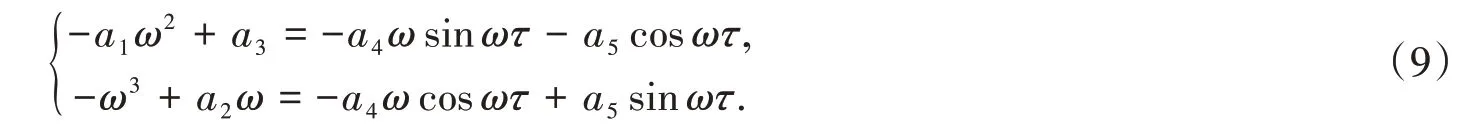
则

因此,根据Rouche[8]定理及其相关定理可得以下结论.
定理2假设满足条件H(1),H(2),H(4)和H(5),那么以下条件成立:
(i)当τ∈[ 0,τ0)时,时滞HR神经元式(1)在平衡点E0(x*,y*,z*)处是渐进稳定的;
(ii)当τ=τ0时,时滞HR神经元式(1)在平衡点E0(x*,y*,z*)处产生Hopf分岔;
(iii)当τ∈[τ0,+∞)时,时滞HR神经元式(1)在平衡点E0(x*,y*,z*)处是不稳定的.
3 数值模拟
在本节,将对第1 节和第2 节中所获的结论给出数值模拟,在数值模拟之前,首先对原时滞系统式(1)中的各个系数进行赋值:
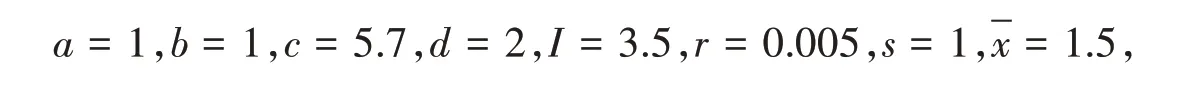
代入HR神经元式(1)得到

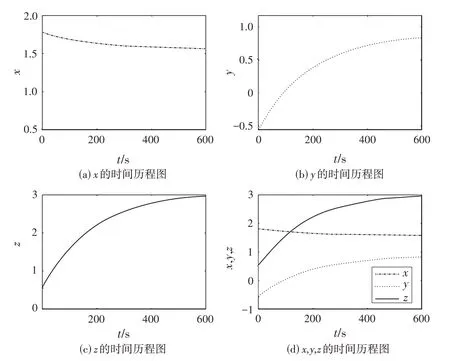
图1 式(1)的时间历程图( τ=0)
当τ>0时,易知条件H(4)和H(5)满足,通过计算求得ω0=1.06,τ0=1.95,所以当τ=1.85 <τ0=1.95时,式(19)在平衡点E0(1 .552,0.883,3.052)处是渐进稳定的.如图2,这里的初值为( 2.38,2.38,2.38).
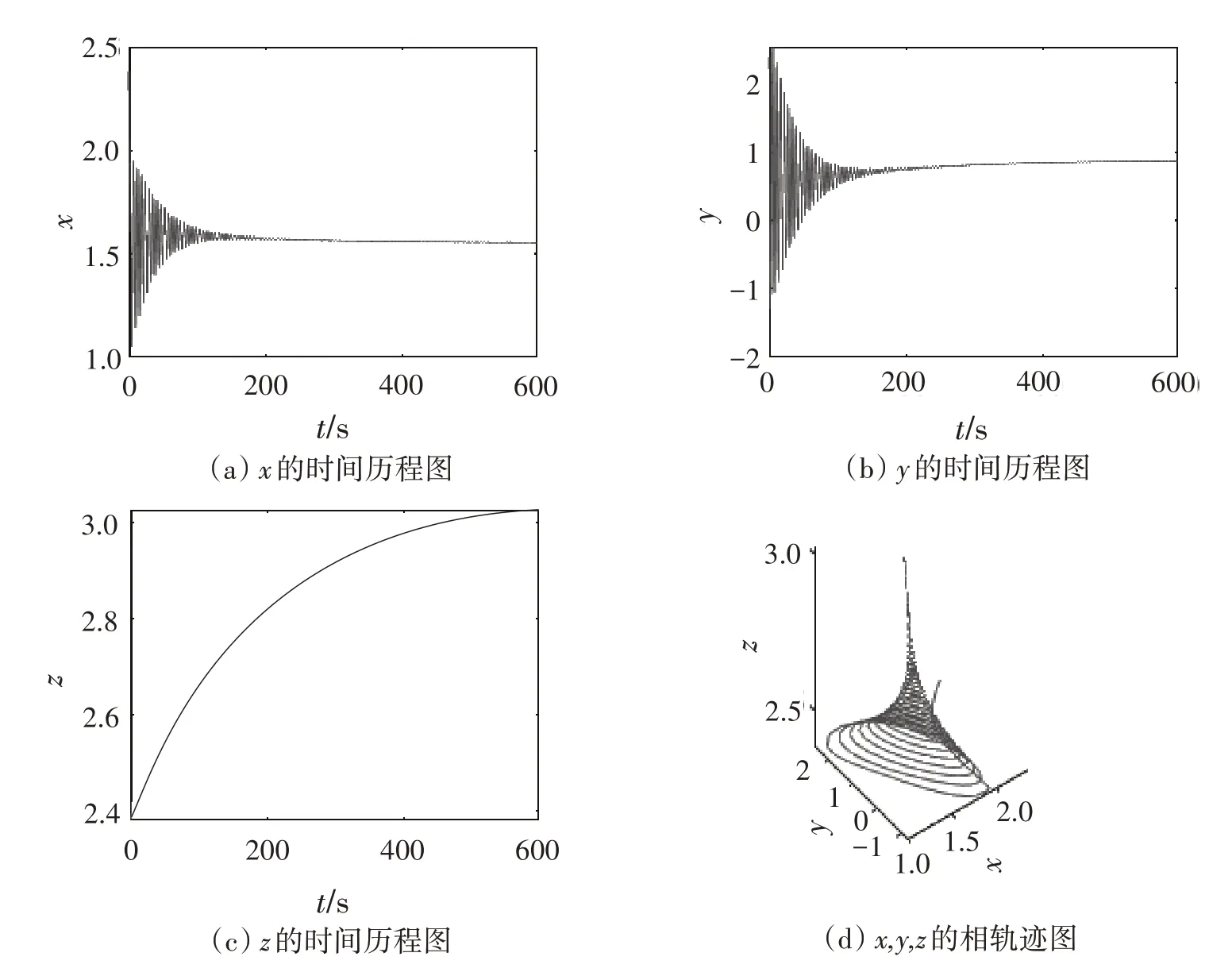
图2 式(1)的时间历程图和相轨迹图(τ=1.85)
当τ=2.01 >τ0=1.95 时,式(19)在平衡点E0(1 .552,0.883,3.052)处是不稳定的.如图3,这里的初值为( 2.38,2.38,2.38).

图3 式(1)的时间历程图和相轨迹图(τ=2.01)
4 结论
本文主要提出了一类具有时滞的HR 神经元模型,探讨了HR 神经元模型正平衡点的存在条件,通过分析HR神经元模型的特征方程根的分布,推出了模型产生Hopf分岔的条件.发现当时滞小于临界值时,HR 神经元模型是渐进稳定的,而当时滞大于临界值时,HR 神经元模型失去稳态并且产生Hopf 分岔.最后,对所获得的结论进行数值模拟,进一步验证了理论的可行性.但对于Hopf分岔的性质,有待进一步的研究.

