具有非线性自食的Lotka-Volterra竞争系统的全局稳定性和分支研究
刘楚蕾 ,许丽莉 ,雷朝铨*
(1.厦门大学 数学科学学院,福建 厦门,361005;2.宁德师范学院 数理学院,福建 宁德,352100)
在文献[1]的研究基础上,得知自食是一种普遍存在于自然界中的生活史特性,其看似违背常理,实则具有调控种群规模、调配食物资源以助于种群生存的积极作用[2-5].受文献[5-7]的启发,文献[1]提出了一类具有非线性自食的Lotka-Volterra竞争模型

其中:x(t),y(t)分别表示t时刻两个竞争种群的种群密度;r,b,m,n,α,β均为正常数,r,b分别表示x和y种群的内禀增长率,α,β分别为两种群各自的种内作用系数,m,n分别为两种群各自的种间作用系数;c为自食率;c1为自食利用率;d为半饱和参数;表示因自食导致的能量损失,c1x表示自食所带来的能量流入.文献[1]探讨了平衡点的存在性和局部稳定性问题,但对平衡点的全局稳定性和系统的分支现象没有进行研究,旨在对这两个问题进行探讨.
1 平衡点的存在性和局部稳定性
这里先叙述文献[1]中关于式(1)平衡点存在性和局部稳定性的相关结果.


2 平衡点的全局渐近稳定性和分支分析
在文献[1]的基础上,进一步讨论各个平衡点的全局稳定性,并给出一些平衡点全局渐近稳定的充分条件.
2.1 全局渐近稳定性
定理1在式(1)中,若满足以下条件之一:

则E1(x1,0)是全局渐近稳定的.
证明对于式(1),设
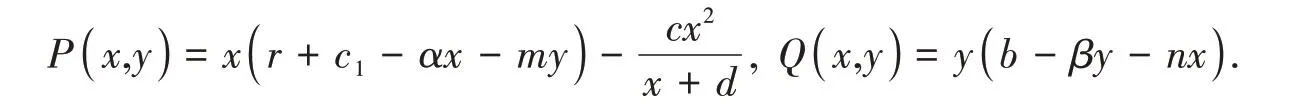
考虑Dulac函数D(x,y)=x-1y-1,则

由Dulac判别法,式(1)在第一象限内不存在闭轨线,因此系统不含有极限环.
当条件1)、2)或3)成立时,由引理3,E1(x1,0)是局部渐近稳定的,而由引理2,E0(0,0)为不稳定结点,而由引理为鞍点,由引理1,系统此时不存在正平衡点,又因为系统并不存在极限环,可知在第一象限内的解均趋于边界平衡点E1(x1,0),因此E1(x1,0)是全局渐近稳定的.


2.2 分支分析


3 结论
在文献[1]中提出了一类具有非线性自食的Lotka-Volterra 竞争系统,探讨了系统平衡点的存在性和局部稳定性,发现系统可能存在2个正的平衡点.
进一步通过构造适当的Lyapunov 函数以及借助Dulac 判据,给出了系统各个平衡点全局稳定的充分性条件;其后,证明了系统在适当的条件下可以发生鞍结点分支.
众所周知,经典的Lotka-Volterra 竞争系统不可能有鞍结点分支,正平衡点只有一个,这表明在考虑了非线性自食后,系统的动力学行为变得非常复杂.
后续将进一步提出具有阶段结构的非线性自食的竞争系统,并研究系统的动力学行为.

