基于有限元分析的光学仿真实验
敖 晖,颜文悦,黄光彩,毋 剑
(1.宁德师范学院 数理学院,福建 宁德 352100;2.上海大学 机电工程与自动化学院,上海 200444)
虚拟仿真实验教学是在新时代高等教育内涵式发展背景下,实验教学主动适应新技术革命性变化,提升新时代大学生的创新精神、实践能力和社会责任感,培养卓越拔尖人才的重要举措,是中国高等教育人才培养推进“智能+教育”的积极探索,是推动人才培养质量提升的新的生产力,对高等教育发展具有重要的全局性意义[1-6].虚拟仿真实验借助计算机仿真软件构建虚拟现实的仿真实验教学环境,有助于突破实验者对客观条件的依赖性,大大增强了教学的趣味性,它能将具有复杂性、危险性、破坏性等特点的实验完美、直观地呈现出来,使实验者在感性充分认识的基础上,加深对知识的理解认识[7-11].光学实验是物理学专业知识的重要组成部分,具有一定的抽象性,实验者往往较难充分理解.因此,将虚拟仿真实验引入到光学实验教学当中势在必行.随着技术的日益发展使得虚拟仿真实验的仿真效果越来越好,实验者在虚拟的世界中能够获取的感知功能越来越丰富,实验教学效果也更好.特别是有限元仿真软件的日益成熟,使得通过对光学实验的有限元分析仿真,建立虚拟仿真实验成为了可能[12-16].
本文利用有限元仿真软件,对光学中的等厚干涉实验进行有限元分析研究,建立虚拟仿真实验,并得到实验现象与实验结果,把抽象内容形象化,结合实际实验结果,加深对光学知识的理解,大大提升了实验教学效果.
1 等厚干涉-牛顿环实验基本理论
1.1 光路图及干涉条件
牛顿环仪是由一个曲率半径很大的平凸透镜与一个平板玻璃叠在一起构成的,当平凸透镜的凸面和一个平板玻璃接触在一起时,它们之间就会形成一层空气薄膜,其厚度由中心接触点到边缘逐渐增加,如图1 所示.当波长为λ的光线垂直照射到薄膜上时,就会形成反射和折射两束光,折射光在薄膜的下表面反射后,又经上表面折射,与上表面的反射光产生干涉.若将空气薄膜的厚度设为h,则两束光的光程差为
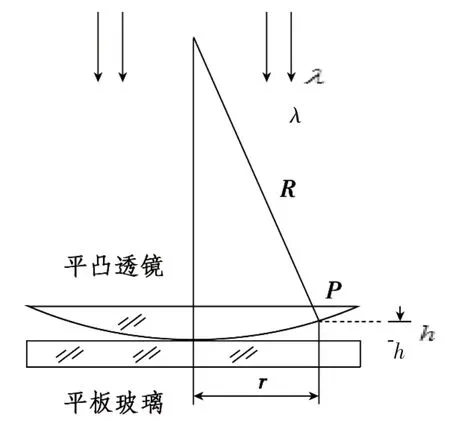
图1 牛顿环光路图

式中,λ2是光线由光疏媒质到光密媒质反射时产生的半波损失.两束光相互干涉的条件为

由于光程差ΔL取决于薄膜的厚度h,h相同的地方干涉图案相同,形成等厚干涉条纹,如图2所示.

图2 等厚干涉条纹关系图
由于接触点O处的空气层厚度h=0,光程差,因此等厚圆干涉条纹的中心是一暗斑.
1.2 透镜曲率半径的求取
由光路图的几何关系图可求得,待测透镜的曲率半径为

由式(3)可知,若已知λ,测得第k级暗条纹的半径rk,便可求得透镜的曲率半径R;若已知R,测得rk后,也可求得入射光源的波长λ.但在实际实验过程中,精确求得rk的难度较大,因此,可取同级暗条纹直径Dk来替代半径rk,则可将式(3)写成

若m与n级暗环直径分别为Dm与Dn,有

式(5)和式(6)相减,得

2 等厚干涉的有限元分析
2.1 三维建模及材料添加
本文所使用的牛顿环仪曲率半径为855.1 mm,选用的入射光源是波长为589.3 nm 的钠黄光.实验装置如图3、图4所示.

图3 牛顿环仪

图4 实验装置图
通过有限元软件射线光学模块进行三维建模,设置平凸透镜曲率半径为855.1 mm,模型如图5、图6所示.并设置平凸透镜与平板玻璃的折射率为1.5,中间空气薄膜的折射率为1.000 29.

图5 三维模型网格剖分图
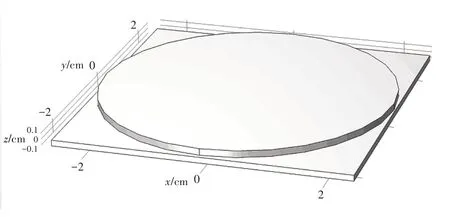
图6 三维模型俯视图
2.2 模型求解
通过射线光学模块添加波长为589.3 nm的光源激励,并设置好边界条件,求解可得如图7所示的干涉图案.
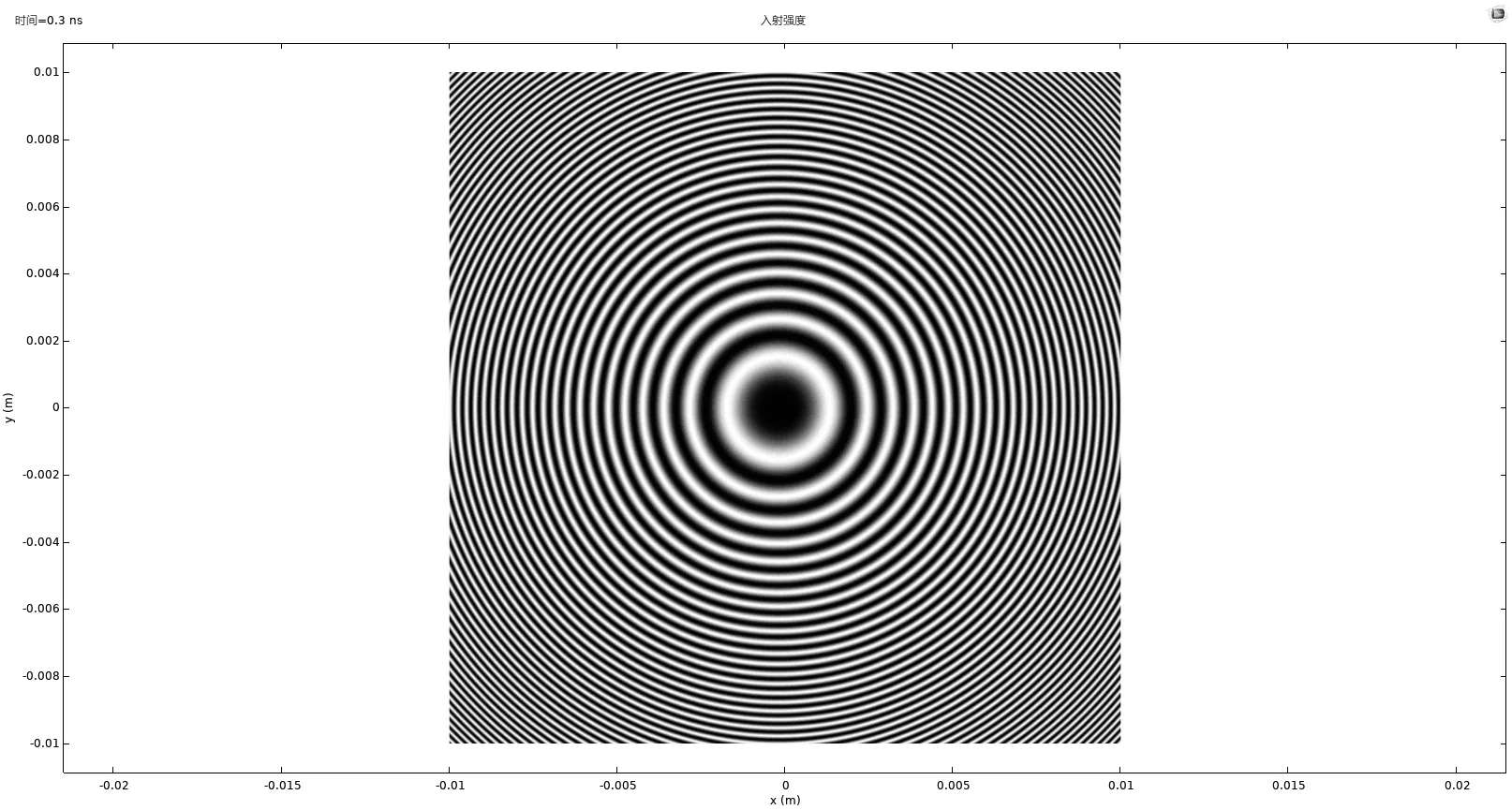
图7 有限元仿真所得干涉图案
对图7 干涉条纹进行分析计算可得表1 数据结果.由于在仿真实验中没有使用读数显微镜,数据都由计算机精确读取,因此只要测定A 类标准不确定度即可通过表1 数据使用间接测量不确定度的方法求得实验的不确定度为24.7 mm.该牛顿环仪的曲率半径仿真实验结果为R=()833.9 ± 24.7 mm,仿真结果的相对误差为2.48%.

表1 有限元仿真分析测得条纹的数据
同时,通过实验室中实验设备的操作、测量,可得到如图8所示的干涉条纹.实验中数据由读数显微镜读取,其总不确定度由A 类标准不确定度和B 类标准不确定度合成.通过计算表2 的条纹数据,使用间接测量不确定度的方法可求得实验的不确定度为10.2 mm,该牛顿环仪的曲率半径实验结果为R=( 876.6 ± 10.2)mm,实验结果的相对误差为2.51%.

图8 实验室所得干涉条纹

表2 实验室中测得条纹的数据
有限元分析软件中的射线光学模块将光波作为射线处理,通过求解位置和波矢的一组常微分方程来追踪经过模拟域的射线,虽然必须对射线经过的域进行网格剖分,但可以使用非常粗化的网格,并不影响求解结果.通过以上两组数据的对比就可看出,仿真所得的数据与实验室所得的真实数据基本是一致的,仿真结果是可信的.
3 有限元仿真App的开发
有限元分析软件中自带了强大的App 开发器模块,研究者可根据不同的需求开发更为直观的仿真操作界面,实验者在交互式的操作界面上修改App所提供的模型参数或激励条件,就可求得对应的仿真结果与现象.本文通过App开发器中的表单编辑器创建了曲率半径、入射波长等变量参数,并设置了绘制几何模型、网格划分、计算求解等按钮.App 开发完成后可挂入浏览器,实验者可上网通过修改App提供的参数,点击计算求解,便可查看相应的实验结果与现象,如图9所示.
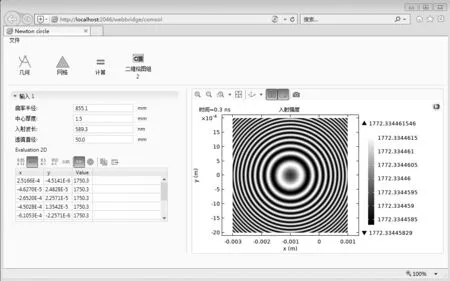
图9 App在浏览器中的测试图
在本文研究的基础上,对其他光学实验和现象进行有限元仿真分析,并进行相应的App 开发,就可以为实验者提供完整的光学虚拟仿真实验,在进入实验室前就能够事先了解实验概况,可大大提升其实验兴趣,从而提高实际实验效果.
4 结束语
本文以等厚干涉实验为例探讨了通过有限元软件模拟仿真光学现象,建立了相应光学虚拟仿真实验项目的过程,研究结果表明,光学现象通过有限元仿真所得到的数据与实验室测得的数据是一致的,仿真的结果真实可靠.此外,利用有限元软件App 开发功能,将整个仿真过程打包成App 软件提供给实验者,实验者可以在进入实验室前进行实验操作、预习,加深对实验原理的理解.本文工作为后期建立光学虚拟仿真实验奠定了基础.

