需求响应视角下有源配电网分层分区切负荷方法

徐俊俊，陈洪凯，张腾飞，王 冲

（1. 南京邮电大学自动化学院／人工智能学院，江苏南京 210023；2. 河海大学能源与电气学院，江苏南京 211100）

0 引言

配电网处于电力系统末端，其运行状况直接影响用户体验和供电可靠性，当配电网发生线路故障或出现功率缺额时调度员需快速切除部分负荷以增强系统弹性，从而保障系统整体安全可靠运行［1-3］。近两年随着电力、煤炭市场供应持续偏紧，多种不利因素导致大部分地区开展不同程度的“拉闸限电”，甚至出现传统“一刀切”式的切负荷方案，这直接影响了社会的正常经济发展和用户生活水平［4］。国务院第599 号令明确了切负荷等同于故障损失负荷，过分切负荷需承担相应的电力安全事故责任［5］。因此，在确保配电网安全稳定运行的前提下，如何精准、快速地实施切负荷操作以确保非故障区域持续供电，同时尽可能考虑需求侧用户满意度与经济损失，是电力部门亟待解决的难题。

与此同时，随着新型电力系统相关建设工程的进一步落实，高渗透率分布式电源DG（Distributed Generator）加快接入配电网，传统配电网结构发生了改变，也给传统切负荷方案的可靠性带来了更大挑战。文献［6］在实时估计DG 出力的基础上，对低频减载中各馈线的负荷进行优先级排序，针对最优切负荷目标选择相应的馈线中断；文献［7］提出了一种在DG 出力最大场景下减少负荷切除量以稳定频率的策略，该切负荷策略是基于频率信息、频率变化率和负荷历史数据。实际上，在电源侧利用DG 提高切负荷的精准控制能力有限，配合负荷侧需求响应技术能够在更大程度上挖掘柔性负荷潜力；文献［8］分析了用户负荷特性，提出了一种以配电侧新能源消纳和运行成本为主体、负荷侧为从体的主从博弈模型，但未考虑配电网运行的安全可靠性；文献［9］提出了一种针对功率缺额下需求响应资源的负荷聚合模型和分散控制方法，并未对大功率缺额场景下的负荷切除策略进行分析；文献［10-11］从居民舒适度、需求侧响应资源、配电网运行经济性等不同角度，通过需求响应、分布式调控等不同策略实现配电网的负荷控制。然而上述配电网负荷调控策略涉及的变量较为单一，并未综合考虑DG 接入、用户满意度和需求响应成本等因素对配电网切负荷策略的影响，同时也没有对切负荷后系统运行经济性和可靠性进行分析与讨论。

另一方面，由于当前省级电网基本实现分层分区运行，因此配电网分区切负荷已成为大规模电网切负荷效率提升的重要手段。文献［12］提出了一种全局集中优化与分区自治相结合的主动配电网协调控制策略，实现了电网实际运行中的无差控制。文献［13］基于电网已有的分层分区架构，采用“主站-子站”配置，主站接收各配电子站的运行信息并下发切负荷指令，但并未建立分区切负荷的目标函数，难以实现负荷的精准切除；文献［14］在文献［13］的基础上，基于稳态模型构建了输-配2 级分层分区切负荷方案，制定了考虑DG 影响的配电网精细化切负荷策略；文献［15］提出了一种综合考虑调控主站、配电子站调控单元和子区域调控终端的多层分区协调控制策略。以上对配电网分区负荷控制的研究取得了一定的成效，但也缺乏对配电网分区后各子区域间协调控制时信息传递有效性的考虑，切负荷方案需要消耗大量的通信资源，导致整体切负荷效率不高。

综上所述，本文侧重考虑需求侧用户响应成本与满意度，并利用事件触发机制驱动的分层分区协调思想实现对有源配电网切负荷的快速、精准控制。通过边划分方法将配电网合理划分为若干子区域（子厂站），并建立以用户满意度最大和全网需求响应成本最低，兼顾各子区域内安全运行、用户响应意愿的有源配电网切负荷模型。一旦接收到配电主站发出的切负荷指令，则各配电子区域根据本地运行情况采用事件触发机制与其他子区域进行通信与数据交互，可以确保在其他配电网子区域安全运行的前提下完成对故障区域的精准切负荷，并降低不同区域间的数据传输量，从而有效提升配电网切负荷效率。

1 面向快速精准切负荷的有源配电网分层分区协调控制

1.1 总体架构

基于电力系统现有分层分区调度管理体系，搭建适用于精准快速切负荷的有源配电网分层分区协调控制架构如附录A 图A1 所示。该控制架构主要包括决策层、协调层和设备层。其中：决策层主站模块配合协调层各配电子站模块进行数据交互，并在检测到系统发生功率缺额时将切负荷指令下达至不同的控制区域子站；协调层各配电子站模块一旦接收到上层切负荷指令，则快速启动本地建模与优化方案，利用该区域内可中断负荷、DG 出力等信息计算本地切负荷量，并将计算结果与需求通过主站与其他配电子站共享，完成对区域内负荷节点开关指令的精准下发；设备层则在接收到协调层下发的负荷开关动作指令后，执行本地负荷切除操作。

实现对大规模配电网的合理分区是提高切负荷指令下达精确性的前提条件，同时考虑到设备层各设备上传至配电子站的信息量较大，且各配电子站需要不停地进行信息的交互与迭代更新，因此切负荷过程中海量数据的存储与传输易受到现有带宽的限制。基于此实际需求，本文借助复杂网络理论中的边划分方法将配电网划分为若干子区域，并提出基于事件触发机制的有源配电网分层分区协调控制方法，在有限通信资源下确保切负荷的精确性和快速性。

1.2 基于社区发现边划分的配电网分区方法

配电网拓扑结构和系统空间分布具有高度相似性［16］，借鉴输电网已有的最优分区理论，节点间电气耦合关系的强弱可以通过节点间电气距离的大小表示。对于网络中直接相连或存在耦合关系的节点i、j，定义两节之间的电气距离ωij为：

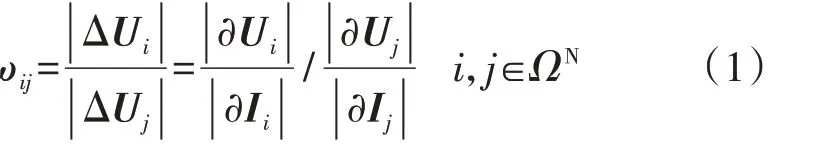
式中：|Ui|、|Uj|分别为节点i、j的电压相量Ui、Uj的幅值；|Ii|、|Ij|分别为节点i、j的注入电流相量Ii、Ij的幅值；ΩN为网络所有节点集合。

当节点i、j之间不存在直接电气联系时，令ωij=0，因此可以将配电网模型抽象为具有N个顶点的等效拓扑结构G，并将节点间的电气距离信息导入N×N维的邻接矩阵A中，其元素Aij=ωij。此外，节点注入电流相量和节点电压相量间还存在如下关系：

式中：Yij为导纳矩阵中以复数形式表示的节点i、j对应的元素；Ωi为网络中与节点i直接相连的其他节点集合。

通过定义配电网电气距离，并结合社区发现理论中的边划分方法以及模块度概念，可实现对配电网网络的优化分区。

对于包含N个节点、L条馈线的配电网拓扑结构，本文假设第τ条馈线以节点i、j作为2个端点，则可以构建N×L维的关联矩阵B，其元素Biτ和Bτj如式（3）所示。

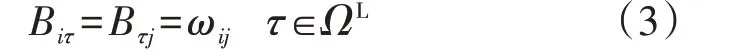
式中：ΩL为网络中所有馈线的集合。

此外，定义节点i的度κi、节点j的度κj如式（4）所示。

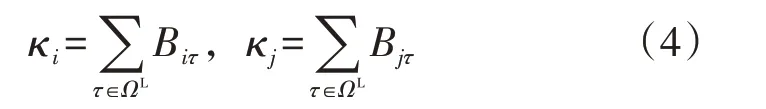
由式（4）可看出，本文定义的节点度实际为与该节点相连的所有边的加权和。

若第υ条馈线也以节点i、j为2 个端点，则可构建基于边的L×L维邻接矩阵C，其元素Cτυ如式（5）所示。

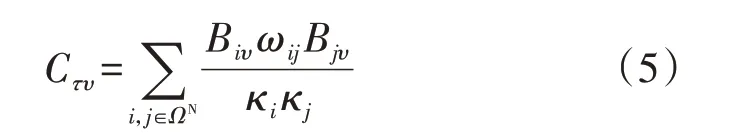
可以将矩阵C定义为具有L个顶点的加权无向网络，也可称之为社区［17］。文献［17］采用复杂网络理论验证了以下结论：以C为邻接矩阵并结合基于模块度值大小的网络最优边划分方案，和采用最优顶点的思想对网络模块化所取得的划分效果基本一致。基于此考虑，定义加权无向网络的模块度值Q如式（6）所示。

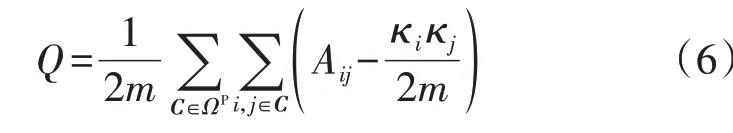
式中：ΩP为网络中所有社区的集合；m为网络中所有边的加权和。Q越大，表示不同社区间的联系越紧密。

将配电网络中的N个顶点初始化为N个社区，各社区之间相互独立。对于社区C1中的顶点i和相邻社区C2中的顶点j，将顶点i从C1移动至C2形成新的社区和，具体过程如图1 所示。

图1 顶点i移动至相邻社区顶点j的过程示意图Fig.1 Process of Bus i moving to Bus j in adjacent community

针对移动后的网络计算其网络模块度的变化量ΔQ。当ΔQ＜0时，表示顶点i仍在原社区C1中。该移动方法按照顶点编号递增的方式对每个顶点进行迭代，当满足模块度Q不随顶点的变化而增加，即模块度Q达到最大时，停止迭代并输出网络初步分区结果。对于经过上述初步分区后的各“社区”，将其视为加权顶点，顶点的权则表示“社区”的规模，包括该“社区”中的节点个数、边的个数等。将“社区”之间的边视为无权边，由于划分后各“社区”之间的电气联系已相对较弱，而合并问题的重点在于网络规模相近，相关理论分析［17］验证了如果各子区域规模进一步接近，则可进一步提高分区算法的计算效率。因此，合并问题可等价为加权点-无权边的均衡图划分问题，即求解子区域的最大规模与最小规模之比，定义目标函数如下：

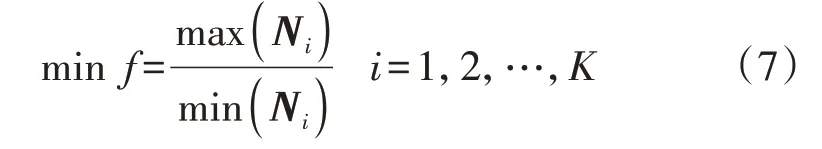
式中：K为指定分区个数；Ni为子区域i的规模。

在非重叠式分区中，顶点的权重和最终分区数目已知，则式（7）可转化为：

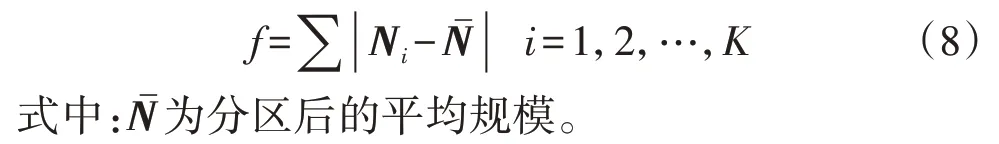
针对以上优化目标，可采用寻优算法求解最优划分方案。本文将该优化问题拆分为子问题：从度(κ)最少、权(w)最小的顶点v开始，在其相连顶点合集Sv中搜索顶点v′，该顶点v′满足当顶点v并入后，顶点的加权和趋近Nˉ，即搜索唯一的v′∈Sv，使式（9）中的Δ取得最小负值。

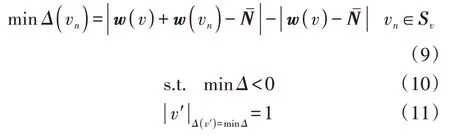
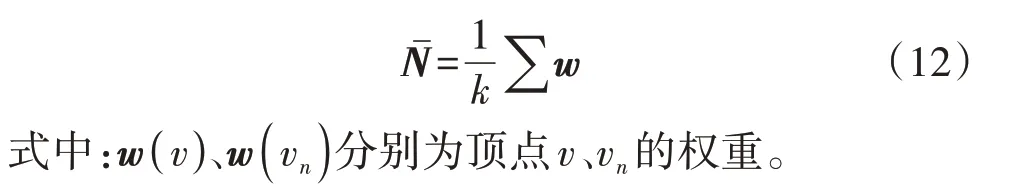
如果Δ取得最小负值且唯一，则将顶点v并入顶点v′，其权值变为原值与顶点v权值的加权和；如果Δ的取值不存在负值，即将v并入Sv中任意1 个顶点，其顶点加权和都不趋近于目标值Nˉ，则将其分割作为结果中的1 个子区域；如果Δ取得最小负值但不唯一，则保留v′不变，从除了顶点v外，度最少、权最小的顶点开始，重复上述步骤，最终在初步分区的基础上实现相邻子区域的合并与分区规模的均衡，从而进一步提高大规模配电网分区算法的计算效率。

综上所述，本文所提分区方法不仅考虑节点间电气距离，同时还兼顾划分后的各子区域规模均衡等因素。通过该网络分区方法可将配电网合理分割为多个子区域，为下一步实现基于事件触发机制的配电网快速精准切负荷提供分布式多区域实施框架。

2 考虑需求响应的本地切负荷优化模型

2.1 模型目标函数

对于配电网子区域m的切负荷控制，需要考虑本地需求响应成本，包括切除用户负荷所需的代价和以及当前电网电价。如果切除负荷的总数为n，总的时间为T，则总的需求响应成本f1，m如式（13）所示。

式中：K1、K2为可中断负荷常系数，一般取值为K1=0.002，K2=3.2［18］；Pti，IL为节点i在t时刻的负荷切除量；θi为负荷节点i的可中断意愿，其取值范围为［0，1］，θi值越大，表示中断意愿越强烈。

为避免传统方案存在的切负荷期间易恶化供需双方关系等，需要考虑用户参与切负荷期间的满意度水平，本文将用户参与意愿最大作为所提切负荷模型的另一个目标函数，可表示为：

式中：ω1、ω2分别为目标函数f1，m、f2，m的权重系数，可按照实际情况进行调整。

2.2 模型约束条件

1）支路潮流约束。

本文基于具有递归特性的Distflow 支路潮流方程组来描述辐射状有源配电网络的潮流方程约束，包括节点有功和无功功率注入约束及支路潮流电压方程约束［19］。为了体现切负荷过程中支路开关状态可变的特点，改进的Distflow 支路潮流其节点有功／无功注入约束可表示为：

2）用户响应意愿约束。

模型还需考虑实际用户响应意愿约束，即可中断负荷的运行约束。可中断负荷约束主要包括切除量约束、中断次数约束、中断持续时间和中断时间间隔约束，分别如式（21）—（24）所示。

此外，本文在建立切负荷优化模型时还考虑了电压电流约束、DG 出力约束和网络辐射状运行约束，具体见附录A式（A1）—（A6）。

2.3 模型求解算法

然而等式约束式（27）的存在使该模型仍然是非凸问题，为此，需要采用图2 所示的非凸可行域松弛过程将原模型转化为一个二阶锥规划问题［20］，如式（28）所示。

图2 二阶锥松弛示意图Fig.2 Schematic diagram of second-order cone relaxation

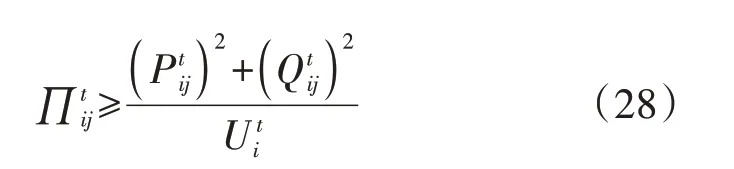
对式（28）进行等价变形，得到标准的二阶锥形式如式（29）所示。

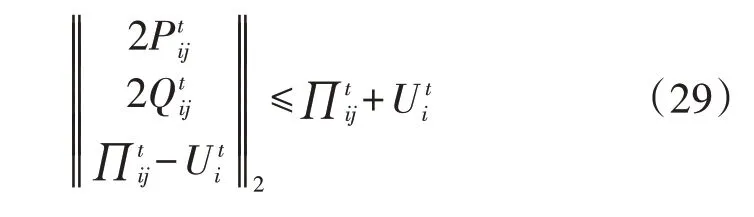
3 基于事件触发机制的有源配电网分层分区切负荷

当配电网某一区域发生线路故障或大功率缺额时，该区域配电子站i快速计算并确定本地切负荷量，根据负荷等级分类以及需求响应需求，利用本区域内等级较低的可中断负荷对支路功率越限、节点电压越限等情况进行调节。特别地，当该区域i内支路功率、电压水平等还没有恢复到安全范围内，亦或本区域内可中断负荷切除量已达到极限值，但却尚未达到预设的切负荷量时，则由子站i向主站反馈需求信息，主站根据负荷裕度选择相邻区域内具有一定调节能力的可中断负荷对其进行跨区域切负荷，此时被选中区域j需将自身状态信息传输到子站i以执行具体切负荷量的计算和优化，确保系统整体运行可靠性。由此可知，相邻子区域是否参与切负荷操作可定义为事件，且该事件执行与否直接与子站切负荷的状态、可中断负荷量、支路功率、节点电压等信息有关。

同时，考虑到配电主站在统筹系统切负荷量时，由设备层各设备模块采集的数据信息需要通过网络传输通道分配至各配电网子站。然而，随着网络自身规模以及源荷储接入规模的不断增加，海量数据的上传与交互极有可能造成通信受阻、传输延时等现象，不利于切负荷指令的高效执行。为了缓解网络通信压力，本文提出了基于事件触发机制的有源配电网分层分区切负荷指令实施策略，每个配电子站设置事件触发控制器和事件触发检测器，每个事件触发控制器独立检测邻接子站传递的数据是否满足所设定的触发函数［21］，且触发控制器会依据触发函数对子站之间的通信进行一定限制，只有满足触发函数的数据才会传输到邻接子站。显然，该方式可有效减少配电主站与子站间、各子站之间的数据传输量，在有限通信资源下完成切负荷指令的接收与实施。

综上所述，本文所提基于事件触发机制的有源配电网分层分区切负荷的实施过程如附录B 图B1所示。

4 算例分析

4.1 算例简介

选取改进的PE&G 69 节点配电网［22］算例对所建立的有源配电网分层分区模型的可行性和有效性进行验证分析，关于该测试网络详细参数设置见附录C表C1—C3。基于1.2节所提配电网优化分区方法计算出该网络的等效电气距离矩阵ω以及模块度值矩阵Q，同时考虑子区域规模均衡、负荷重要度均衡以及分布式电源均衡分布等因素，通过边划分方法可将PE&G 69 节点配电网络划分为如图3 所示的4 个非重叠子区域。图中：子区域①、②以支路3-4为边界；子区域②、③以支路8-9 为边界；子区域③、④以支路11-12为边界。

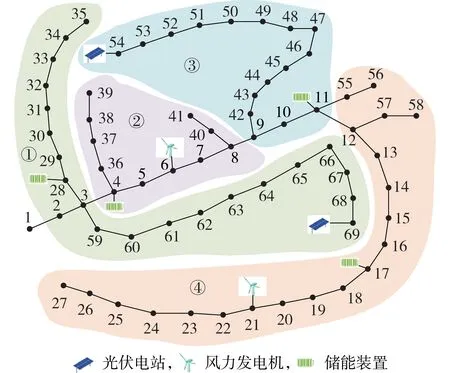
图3 改进的PE&G 69节点配电网系统及分区结果Fig.3 Schematic diagram of modified PE&G 69-bus distribution network and its partition result

此外，考虑切负荷过程中的需求响应成本，对PE&G69 系统中所有负荷节点按重要程度进行分类，具体分类结果见表C2。

为验证所提有源配电网分层分区切负荷方案的可行性和有效性，选取已有的配电网切负荷方案作为参照对象，分别从切负荷精准可靠性与切负荷执行效率2 个维度进行仿真对比分析。所有模型与算法均在MATLAB R2018b 平台进行编程，在主频为2.5 GHz、内存为16 GB的PC上内嵌CPLEX12.5求解器。仿真与对比分析结果如下。

4.2 集中式／分层分区切负荷方案下供电可靠性分析

针对节点69 因故障发生5 MW 功率缺额的情况，传统多目标切负荷方案［23］基于整个配电网全局建模，以全网切负荷成本最小和用户满意度最大为目标函数，在满足潮流约束、节点电压约束、可中断负荷运行约束的条件下，同时按照本文设置的节点负荷参数，在15%的DG 渗透率下采用该方案得到的配电网69个节点的电压水平如附录C图C1所示。图中电压水平为标幺值，后同。显然，按照传统方案执行切负荷操作会造成节点19、20、21、55、59 的电压水平超过安全运行上限值，特别地，节点59 为第一类重要负荷，此类负荷通常是对供电可靠性要求很高的政府部门、医院等重要场所，一旦发生节点电压越限情况极易造成非常严重的社会事件；节点19、20 为第二类负荷，此类负荷电压过高同样会引发比较严重的电力安全事故；而节点21 接入了风力发电机组，该节点发生电压越限可能会造成风力发电机脱网，导致配电网系统出现额外的功率缺额，从而需要切除更多电力用户，引发更大规模的停电事故。

相同测试环境与参数设置下，采用本文所提分层分区切负荷方案时69个节点的电压水平如附录C图C2 所示。由于本文所提方法首先对配电网进行分区，其次采用分层分区协调控制策略，对各子区域配电网执行切负荷操作。由图C2可以看出，所有的节点电压均处于［0.95，1.05］p.u.的安全范围内，不会出现某个节点电压越限现象，满足切负荷后配电网安全可靠运行约束，因此相比传统方案，本文提出的分层分区切负荷方案能够确保配电网在执行切负荷操作过程的用户供电可靠性。

4.3 不同分层分区方案下配电网切负荷结果分析

为便于公平直观地对切负荷结果进行对比分析，基于本文所提分层分区协调架构对文献［23］提出的集中式切负荷方案进行改进，即分4 个子区域对测试系统进行切负荷仿真分析，但依旧定义为传统方案。2 种切负荷方案得到的各子区域在不同时段的切负荷情况如C 图C3—C6 所示，其中稳态负荷为可中断负荷的总量。由图可知：子区域①按照传统方案执行切负荷操作，在负荷高峰时段（时刻12—20），切负荷量接近稳态负荷值，这会导致多数重要负荷节点被切除，意味着用户满意度会降低，同时在用电高峰期间切除负荷也会增加切负荷成本；相比之下，本文方案能够实现全天内平均切负荷，每一时段内的切除负荷比例都不会过高，可以在确保第一类负荷正常用电需求的同时，提高用户满意度，降低切负荷代价；子区域②按照传统方案执行切负荷操作所得的结果比子区域①更差，在2 个时间段（时刻6—9、11—20）内均会出现切除比例过高的现象，而本文方案可以很好地避免该问题；同样地，子区域③、④按照传统方案进行切负荷操作时也会出现不同程度的过切现象，而本文方案亦可以避免此类问题。

另外，2 种不同切负荷方案下配电网需求响应总成本及用户满意度（即切负荷目标函数）汇总如表1所示。

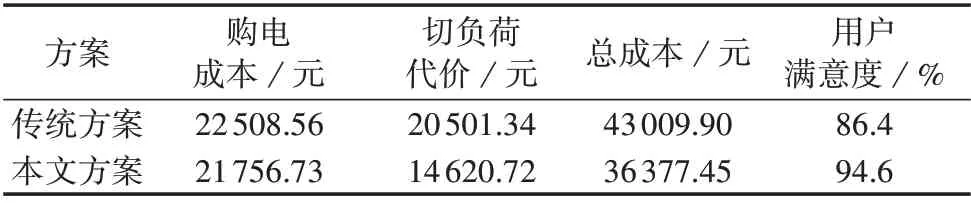
表1 2种不同切负荷方案下的目标函数对比Table 1 Comparison of objective functions between two load shedding schemes

由表1中的数据可知，相比于文献［23］提出的传统切负荷方案，本文所提方案能够在一定程度上降低配电网运行的总成本，同时用户满意度也能保持在较高水平，说明本文所建立的切负荷优化模型不仅能够保证负荷切除后配电网运行的经济性，也能够满足用户满意度的需求。

4.4 采用不同触发机制的切负荷效率分析

目前在电网多区域协调触发控制方面较为常见的是事件触发与周期触发2 种机制，为突出事件触发机制在切负荷过程中相对于周期触发机制的优势，将文献［24］提出的周期触发机制应用于本文的有源配电网分层分区切负荷理论中，在相同测试环境与参数设置下2种触发机制的仿真时间均为10 s，其中：周期触发机制的周期选为0.02 s，同时触发参数设为δ=0；事件触发机制的触发参数设为δ=0.05，在该机制下各子区域的触发时刻如附录C 图C7 所示。由图可知，在给定仿真时间内，可以计算出每个子区域①—④的平均通信时间间隔分别为0.067、0.161、0.794、0.893 s，子区域①—④的最大通信时间间隔分别为1.02、1.5、0.6、0.8 s，各子区域的最小通信时间间隔均为0.02 s，因此，事件触发机制比传统周期触发机制的平均通信时间间隔更长，这在一定程度上会占用更少的通信资源。

此外，表2给出了2种触发机制下各子区域的触发次数汇总情况。由表中的数据可明显看出，本文采用的事件触发机制能够大幅减少各配电子区域之间切负荷信息交互的通信次数，这在一定程度上有利于减小通信网络的数据传输压力，从而提高切负荷过程的效率。

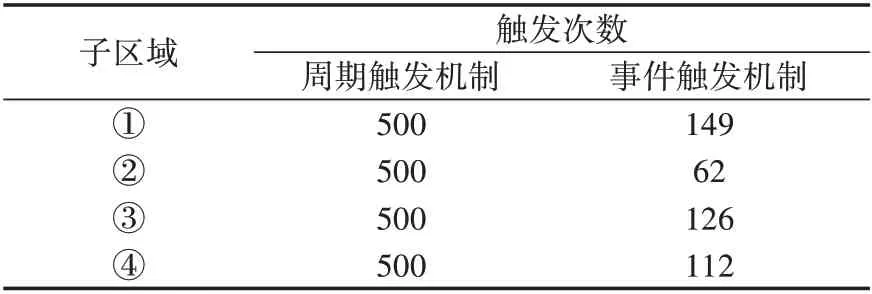
表2 各子区域2种触发机制下的触发次数对比Table 2 Comparison of triggering times between two triggering mechanisms in each sub-area

4.5 不同切负荷算法收敛性对比分析

传统切负荷方案采用集中建模、统一求解的方式对整个配电网全局需求响应成本和用户满意度进行优化计算，而本文所提分层级方案针对分区后的每个配电子区域建模和求解。针对相同的目标函数和约束条件，2 种方案的迭代次数与收敛情况的对比如图4所示。由图可知，本文方案只需迭代6次即可达到最优解，而传统方案需迭代10 次，且其对于需求响应成本的优化效果不如本文所提分层级切负荷方案。

图4 2种方案的收敛情况对比Fig.4 Comparison of convergence between two schemes

同时，为了验证本文所建立二阶锥松弛优化模型的准确性，定义误差指标如下：

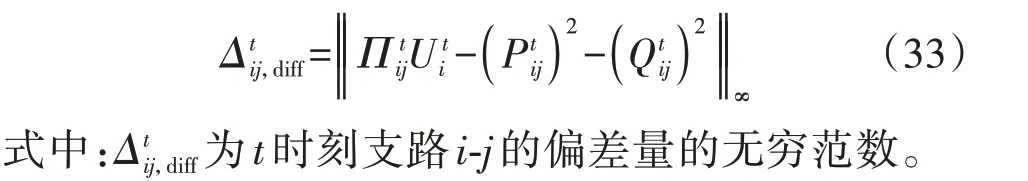
其他参数不变，仅将触发参数设为δ=0（即常规方案采用的周期触发机制）时，系统的误差散点图如附录C图C8所示；触发参数为δ=0.05（即本文所采用的事件触发机制）时，系统的误差散点图如附录C 图C9 所示。由图C8 可知，采用周期触发机制时，系统松弛误差指标为10-8量级；由图C9 可知，采用事件触发模式时，系统松弛误差指标为10-6量级，虽然其误差比采用周期触发机制时大，但依然满足实际配电工程切负荷需求，在实际规划过程中其误差可忽略不计。同时，与周期触发机制相比，本文采用的事件触发机制可以很大程度上减少通信次数，降低数据传输量。综上所述，本文所提事件触发机制能够在节省通信资源的基础上保证切负荷算法的收敛精度。

5 结论

本文针对传统切负荷方案存在不足，提出了基于事件触发机制的有源配电网分层分区切负荷协调控制策略。在动态时间尺度下，构建了以用户满意度最大和全网需求响应成本最小为目标函数，综合了DG 出力、可中断负荷和配电网潮流等约束的有源配电网多目标切负荷模型，并基于二阶锥松弛技术将模型的NP 难问题转化为易于求解的线性规划问题。通过算例对比分析验证了本文所提切负荷方案能够在降低切负荷成本、提高用户满意度的同时，进一步提高切负荷指令的执行效率，有利于大规模配电网切负荷操作的在线应用。

附录见本刊网络版（http：//www.epae.cn）。