基于模体挖掘与调和函数半监督学习的非侵入式负荷监测

周勇军，吴元香，董智华，胡誉蓉，肖先勇，张 姝

（1. 国网西藏电力有限公司拉萨供电公司，西藏拉萨 850010；2. 四川大学电气工程学院，四川成都 610065；3. 国网西藏电力有限公司，西藏拉萨 850000）

0 引言

在用户与电网的双向互动服务模式［1］中，对用户侧设备用电情况的分类计量是一项基础工作［2］，其中非侵入式负荷监测NILM（Non-Intrusive Load Monitoring）是所采用的一种典型方法，该方法是指利用用户供电总线处的数据分析出详细的设备使用状态等信息。这些信息可以帮助用户通过更换节能电器、调整电器参数、错峰用电等方式来减少电费。用户也可将这些信息共享给电力企业，以获取更多的增值服务。通过NILM 方法，电力企业能更加详细地掌握用户的用能信息，科学地制定区域电力系统的发展规划与供电计划［3］。

现有关于NILM 方法的研究，大多需依靠对单台设备的单独测量来建立负荷特征库进行模式识别，但特征库是侵入式收集的，会影响用户正常的生产生活，因此需要一种可以非侵入式收集、提取和存档任意用户每台设备唯一特征向量的收集方法［4］。随着用户设备类型与数量的增加，具有相近运行特征的设备也逐渐增多，当这类设备交叉投切时，准确分析设备运行时间极为困难。文献［5］通过大量的算例验证了基于设备运行窗的NILM 方法准确率更高，但其没有对设备窗的选定进行说明。文献［4］根据历史标记事件数据、相位、设备可能的运行时间段等信息以及聚类算法确定设备的运行窗，在一定程度上提升了分析精度，但辅助信息过多且实时性不足。文献［6-7］分别通过二分图模型与迭代运算进行事件匹配，但均未考虑多状态和相近功率的设备。

负荷特征量是用来区分设备类型或运行状态的重要标签，主要包括设备运行时的稳态特征和状态转换时的暂态特征。其中，稳态特征包括功率需求、谐波特性、电压-电流轨迹、电压和电流的波形参数等。暂态特征包括瞬态功率、谐波和电压波形参数等［8］。但波形参数与谐波分析都需要较高的采样频率，对配置的测量设备要求较高，这也会导致存储与分析成本的增加，因此，有必要提取分析更为实用的负荷特征量，以满足NILM方法推广应用的需求。

最经典的负荷识别方法是以单台设备的特征向量为对象进行模板匹配［9］，并根据与期望值的偏差情况进行判定。随着对准确度需求的提升，基于判别函数的分类法被用于负荷识别中，包括基于线性函数的支持向量机［10］、基于非线性函数的神经网络［11］以及基于概率函数的贝叶斯［12］分类法。但这些监督类方法对标记样本的数量需求较高，使得相应的NILM 方法在应用中面临成本高昂、实施繁琐以及居民舒适度低等问题［13］。如何降低该过程的工作量，是NILM 方法广泛应用面临的关键难题。近年来，模糊聚类［14］与隐马尔可夫模型［15］等不对样本进行标记的无监督类方法也被应用到NILM 方法领域，但这类方法存在分类准确度较低且分析结果需要人工标识等新问题。

为此，本文从NILM 方法的实用性角度出发，提出一种基于模体挖掘与调和函数半监督学习的NILM 方法。首先，基于1 Hz 低频采样的功率数据，利用设备运行的基本约束与事件发生的先后逻辑，确定唯一匹配的设备运行窗并建立设备特征库，对不能唯一确定的匹配事件，以模体挖掘法分析所有的可能性；然后，根据不同类型设备开启与稳定运行时的差异，进一步提取设备运行窗中的特征向量，并利用对标记样本需求少的基于调和函数的半监督学习算法对设备类型和运行状态进行识别；最后，基于参考能量分解数据集REDD（Reference Energy Disaggregation Data set），分别从事件匹配和设备识别的角度与其他NILM 方法进行对比，验证本文所提方法的优越性。

1 基于模体挖掘与调和函数半监督学习的NILM方法架构

本文所提基于模体挖掘与调和函数半监督学习的NILM 方法是根据设备投切时在用户总功率曲线上产生的阶跃量，利用完整的设备运行基本约束、事件发生的先后逻辑与模体挖掘，对所有可能的确定设备的运行过程进行划分，并在设备运行窗中利用不同类型的设备在开启瞬态与稳定运行时的波动差异等特征量对各类型设备进行识别的方法。该方法的具体实现流程如图1 所示。其中，基于滑动窗的双边累积和事件检测方法［16］检测设备投切与状态变化的时刻ti与对应的功率阶跃量ΔPi，判断功率阶跃量的阈值η=40 W。

图1 本文所提方法基本流程Fig.1 Basic process of proposed method

2 基于时间序列与模体挖掘的设备运行窗划分

从功率曲线的角度，用户设备主要有3 种典型运行过程：单状态设备在开关时具有相近的功率阶跃量；多状态设备在运行过程中会出现多次不同状态间功率的需求变换，如洗衣机、烤箱等；通常状态变化的设备在开关时的功率变化量不同，在运行过程中设备的功率需求不断变化，如变频空调。

2.1 基于时间序列的设备运行窗识别

设备运行窗是指设备从不工作的初始状态到被开启运行，再到最后被关闭重新回到初始状态的数据段。根据定义可知设备运行的基本约束为：设备运行窗的有功功率变化量总和为0；设备在任何状态都不可能以负有功功率需求运行；设备在关闭前一定被打开，这被称为事件发生的时间逻辑，即当检测到一个(ΔPi＜0，ti)的事件时，一定有某一功率阶跃量ΔPx＞0且ΔPx≈|ΔPi|（单状态设备）或ΔPx＞0（多状态设备）发生在ti时刻之前。基本约束对应的单状态和多状态设备的匹配条件分别如式（1）和式（2）所示。

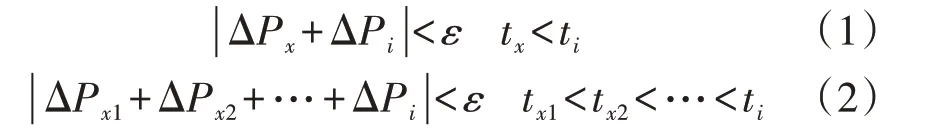
式中：ε为判断匹配的阈值，其值约为10 W。

设备运行窗的确定步骤如下。

1）当检测出用户总功率曲线上的所有阶跃量后，在时间轴上形成一系列以阶跃量ΔPi为符号的事件。

2）读取起始有功功率P0，将未匹配的功率阶跃事件暂时记录于式（3）所示待匹配状态Pw中，待匹配状态功率总和始终大于0，且分析数据段的第一个阶跃量应为正，若为负，则说明某设备的开启事件不在分析数据段内，不能进行运行窗匹配。

3）当检测到ΔPi＜0 时，设置匹配标识n=0，依次假设设备类型为单状态、两状态、三状态等，将ΔPi如图2 所示向前匹配，判断是否满足基本约束式（1）或式（2）。每匹配到1 次，n值加1。当ΔPi与此前的阶跃量全部匹配后，若n=1，对于单状态设备，则说明在此期间没有发生功率需求相近的设备同时投入运行的情况，转至步骤6），而对于多状态设备，则需要进一步分析，转至步骤4）；若n≠1，则发生了功率需求相近设备相继开启或者已经开启的某单状态设备与某多状态设备的状态改变量相近的情况，需等待下一个ΔPi＜0的事件，转至步骤3）。

图2 各状态设备匹配Fig.2 Matching of each state device

4）当功率匹配满足多状态设备约束式（2）时，有可能出现如图3所示的3种情况，图中数据单位均为W。情况1 下不同状态对应的阶跃量绝对值不同，在当前阶段可以唯一确定单个多状态设备类型，转至步骤6）。而情况2 和3 下除了满足式（2）外，还存在多个单状态设备以及某多状态设备与某状态变化量相近的单状态设备重叠的可能性，设备所属类型不能唯一确定，需进行进一步分析，因此将情况2 和3暂时记录于待匹配事件序列式（3）中。

图3 累加和为0的状态窗情况Fig.3 Condition of state window when cumulative sum is zero

5）检测Pw是否小于0：若是，则说明发生了某长时间运行设备关闭的事件，且该设备开启事件发生的时间早于分析数据段对应的时间，此时应调整式（3）中P0与阶跃量的关系；否则，返回步骤3）。

6）根据2.3节步骤输出匹配的设备运行窗。

根据上述步骤可以唯一确定一部分设备运行窗，然后将已确定的设备运行窗从总线数据上移除，以便于分析其他设备运行窗。

2.2 基于模体挖掘的设备运行窗划分

模体挖掘［17］是根据数据挖掘的思想，在时间序列中寻找重复出现的相似片段。数据挖掘以序列符号化的形式进行，即在分析运行窗前将监测数据处理为不同时刻下的功率阶跃量信息。一组能够满足设备运行窗基本约束的功率阶跃量为一个模体，模体挖掘即是在一组符号化信息中挖掘出重复出现的相似片段模体，因此，确定每类设备的第1 个模体是很关键的。

1）在所研究的待匹配事件序列式（3）中，按照时间顺序对ΔPi＞0的事件依次以单状态设备或多状态设备为假设，以设备运行窗基本约束为判定依据，确定第1个模体。

2）每个模体一一向后对应，挖掘监测数据中所有可能的设备运行窗。

3）执行上述步骤，直到分析数据的最后一个阶跃量。

2.3 运行窗数据提取

基于上述分析，监测到的所有设备状态都被划分，一部分是确定的设备运行窗，另一部分是可能的设备运行窗。 确定的设备运行窗将作为已标记样本，用于辨识可能的设备运行窗是否属于某类设备，因此需要从分析结果中进一步提取运行窗数据。

以单状态设备为例，当事件匹配后，设备运行窗中的数据提取过程如下。

1）检查在时间轴上ΔPi与ΔPx事件之间是否有其他设备事件，若没有，则认为该设备在运行时无其他设备交叉重叠开启，该设备运行窗的数据窗口取（tx，ti）之间的数据与tx前一段平稳区段平均值Pav的差值，如图4 所示，图中，Aon和Aoff分别为设备A 开和关的标识。

图4 情况1下数据窗处理示意图Fig.4 Schematic diagram of data window processing under Case 1

2）若在时间轴上ΔPx与ΔPi事件之间有其他设备事件，则除了取差值，还需要将其他设备事件从该数据窗口中移除。考虑到设备重叠运行时大幅度波动的设备会覆盖小幅度波动的设备，影响本文所提的设备运行时稳定波动幅度特征值，因此在数据移除时，若ΔPx与ΔPi之间是ΔPy＞0 的事件，则将ΔPy到ΔPi之间的数据替换为ΔPx到ΔPy之间的数据，反之，则将ΔPx到ΔPy之间的数据替换为ΔPy到ΔPi之间的数据，如图5 所示，图中，Bon和Boff分别为设备B开和关的标识。

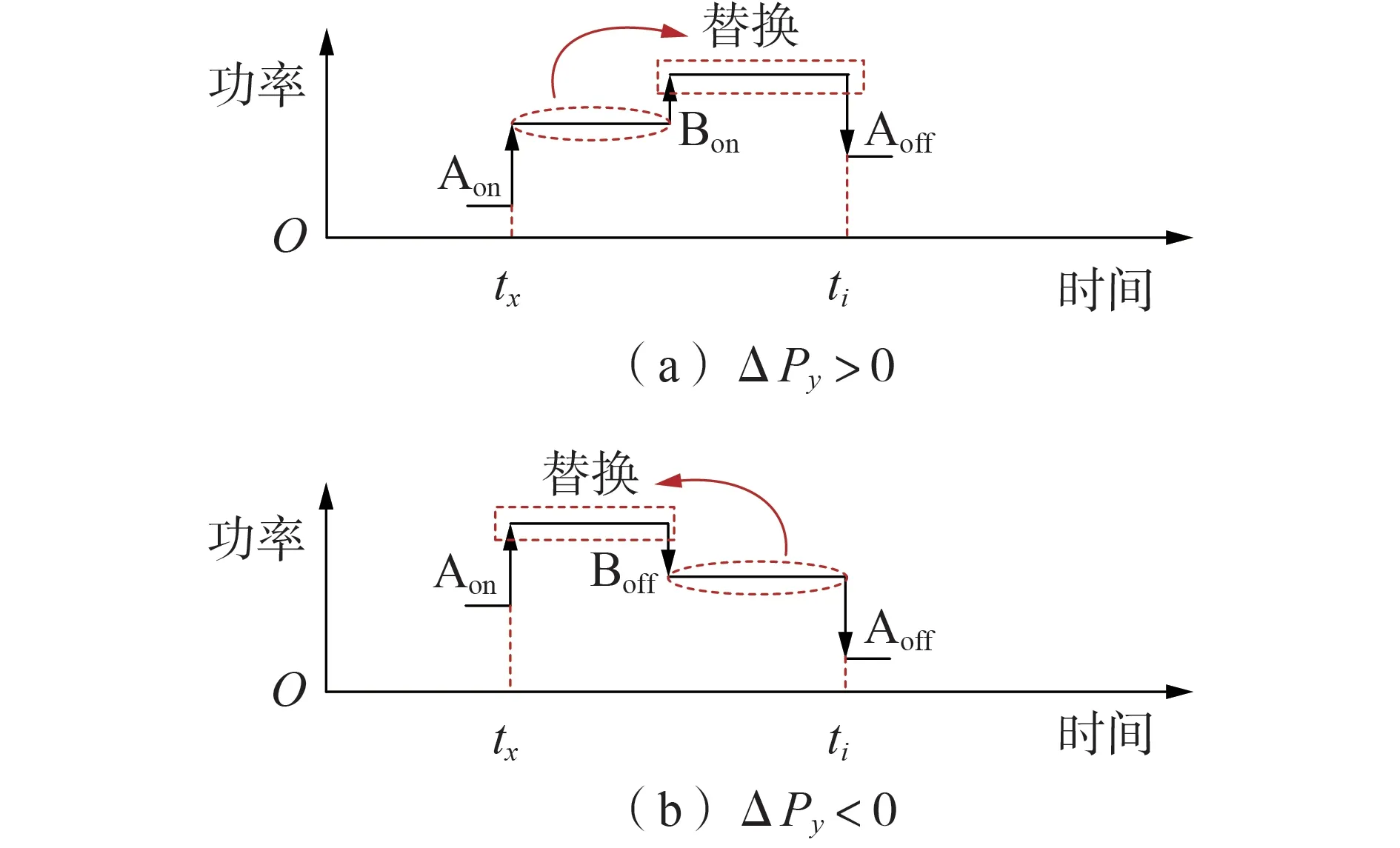
图5 情况2下数据窗处理示意图Fig.5 Schematic diagram of data window processing under Case 2

3 负荷特征量的分析与选取

设备在运行过程中受到主要元器件、设备功能以及人为因素等多方面的影响，将会产生不同的运行特征。在对1 Hz 频率采样的功率数据进行分析时，不同类型设备的表现特征如表1 所示。为表征不同类型设备在开启和运行状态下瞬态和波动情况的差异，本文提出2 个新的负荷特征量进行负荷识别。

表1 不同类型设备的表现特征Table 1 Performance of different types of equipments

3.1 设备开启最大值到稳定运行点的斜率

图6给出了2种典型的设备开启、稳定运行直到设备关闭的功率曲线，设备1 为电阻类或受人为活动影响类设备，设备2 为电机驱动类或电子馈电类设备。图中：Pmax为设备开启时的有功功率最大值；Ps为特征量，表示设备开启到开始稳定运行点的斜率，该变量是考虑不同类型设备在开启时的有功功率需求最大值、稳定运行值与在过渡时间段不同而设定的；Pst为设备开始稳定运行点的功率；Pe为设备最终稳定运行点的功率。

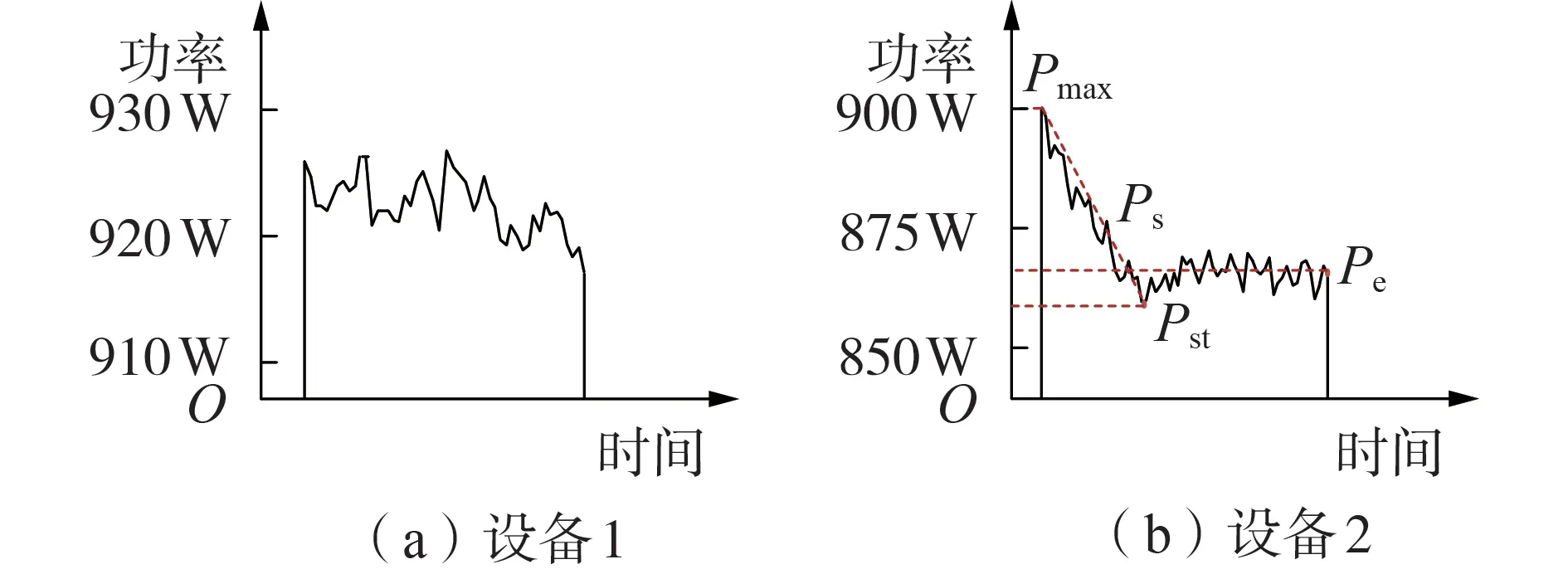
图6 2种典型的设备运行窗Fig.6 Two typical equipment operation windows

为计算Ps，对图6（b）运行窗中的数据进行Δt=1 s的功率变化量分析，如图7所示，图中最大的功率变化量ΔPmax可直接定位，ΔPmax后第1个为负值的变化量对应的有功功率值为Pmax，而最小的功率变化量ΔPmin向前对应的功率值为Pe。

图7 有功功率变化量示意图Fig.7 Schematic diagram of active power variation

由图6（b）可以看出，Pmax到Pst并不是连续下滑的过程，而是存在间歇性的功率值回升现象，因此根据累加和的思想判断Pst的位置。具体计算步骤如下。

1）设置阈值β=3，读取Pmax后的阶跃量，置i=1。

2）判断ΔPi是否为正：若是，则转至步骤3）；否则，令i=i+1，继续向前判断ΔPi的正负。

3）判断ΔPi+ΔPi+1+ΔPi+2是否大于β：若是，则认为已经进入稳定运行区段，输出Pst对应的时刻点；否则，认为仍处于过渡过程，令i=i+1，返回步骤2）。

图6（b）的设备运行窗连续3个变化量相加的结果如附录A 图A1 所示。当分别确定Pmax和Pst对应的时刻点t1、t2后，根据式（4）计算Ps。

3.2 设备稳定运行时的波动幅度

不同类型的设备在Pst到Pe的功率变化量如附录A 图A2所示。由图可以看出，不同设备在稳态运行时波动幅度不同。设备稳定运行时功率变化量（取自设备样本a—d）的频数分布直方图如图8所示，可以看出，数据近似服从正态分布，因此取90%的置信水平将每个运行窗稳态运行时的波动上下限Pf作为设备的特征量。

图8 不同设备功率变化量的频数分布直方图Fig.8 Frequency distribution histogram of power variation of different equipments

3.3 特征向量的构建

每台设备运行窗对应一个特征向量T=［PmaxPsPfPd］，其中，Pd为Pst到Pe之间设备稳定运行时的功率需求。

4 基于调和函数半监督学习的设备类型识别

本文以基于调和函数的半监督学习算法进行运行窗所属设备类型的辨识。该算法的主要思想是在学习训练过程中综合利用已标记和未标记样本，从未标记样本中提取有效的信息来提高学习的性能［18］。该算法在所构建的样本图G上建立连续预测函数的分布模型，充分考虑样例的分类概率，解决了传统离散预测的图割法对相邻类样本误判的问题［19］。此外，该算法的基本思想在后续流形正则化方法的开发中被沿用，是准确性与实用性兼备的一类半监督学习算法。

将全部样本集X（包括已标记样本集XV和未标记样本集XU）构建在包含N个点和E条边的无向图G=（N，E）中，图G中每个点表示一个样本。X共包含N个样本，其中XV的样本数为l，XU的样本数为u，且N=l+u。X中样本xi的特征向量为T，当xi为已标记样本时，其标记值为yi，所有已标记样本的标记值构成集合Y。图G中每条边的权重为wij，表示样本xi和xj之间的相似程度，所有权重构成矩阵W。相似程度一般是通过距离进行判定的，本文用带宽为σ的高斯核函数表示样本特征量间的距离。

对于已标记样本，调和函数值与标记值对应；对于未标记样本，调和函数值满足权重平均原则。设调和函数为f(x)，则：

设计使目标函数值最小的标记预测函数f(x)，对于调和函数而言，它是优化问题式（8）的解。

式中：f(x)∈R 表示调和函数值属于实数域，具有闭合解。式（8）中第1 项为带无穷大加权的损失函数，用于保证已标记样本的值在计算过程中保持不变，第2 项为正则项Ω(f)，用于保证预测函数对样本数据点标记值的平滑性，使得邻近样本的预测标记相似。

设对角矩阵D=(Dij)N×N，其中，i≠j时，Dij=0，i=j时，Dij=∑wij。对应图G的拉普拉斯矩阵L=D-W，令f=[f(x1)f(x2) …f(xl+u)]T。在图G中，数据点被划分为2 个独立的分别标记为正和负的数据组，而分割这2 个独立数据组的边可以表示为正则化函数Ω(f)=fTL f。

拉普拉斯矩阵L可以划分为4个部分：

式中：L为（l+u）×（l+u）阶矩阵；LV、LUV、LVU、LU为拉普拉斯矩阵L的4 个部分，LV为l×l阶矩阵，与已标记样本部分对应，LU为u×u阶矩阵，与未标记样本部分对应，LUV为u×l阶矩阵，LVU为l×u阶矩阵，且=LVU。

类似地，f也可按照已标记和未标记样本分为2个部分：

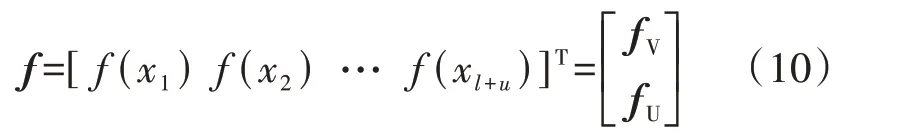
式中：fV为l维列向量，与已标记样本部分对应；fU为u维列向量，与未标记样本部分对应。

正则化函数存在式（11）对应的关系。

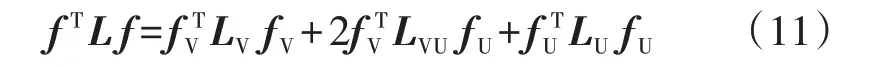
由于正则化函数主要是针对标签中的fU进行求解，对于式（8）中的优化问题也是求极值解，因此将式（11）对fU求偏导并令结果为0，可得：

综上，基于调和函数半监督学习的设备识别步骤为：

1）所有样本的特征向量形成邻接矩阵W；

2）定义已标记样本的调和函数值；

3）计算拉普拉斯矩阵L，根据式（12）计算未标记样本的调和函数值，以此区分设备类型。

5 算例验证

本节使用麻省理工学院（MIT）发布的从真实家庭中收集的数据集REDD［20］，验证工作主要从REDD_house1 和REDD_house3 数据展开，其中有功功率的采样频率为1 Hz。为了测试模体挖掘和基于调和函数的半监督学习算法的性能，从2 个方面进行验证：保持所提方法中其他部分不变，将所提方法中模体挖掘分别替换为文献［6-7］中事件匹配法进行对比；保持所提方法中其他部分不变，将所提方法中基于调和函数的半监督学习算法分别替换为监督类和无监督类算法进行对比。

5.1 模体挖掘验证

负荷识别过程中，样本处理过程为：

1）对每台设备均以5%的已标记样本作为间隔进行7 组测试，其中，每组中正负样本比例和已标记样本比例均相同；

2）为了保证测试结果的准确性，每组测试反复随机选择已标记样本计算10次；

3）将10次测试结果的平均值作为最终的结果。

本节利用式（13）中综合评价指标识别准确度F1对分类精确度进行评价。F1的值越高，说明分析越准确。

式中：p为预测为本类的样本中正确的比例；r为本类样本中预测正确的比例；Tp为样本类别预测正确的个数；Fp为将其他类样本预测为本类样本的个数；Tn为将本类的样本预测为其他类样本的个数。

实验结果如图9 以及附录A 图A3、图A4 所示。在图9 的REDD_house1 中，烤箱、微波炉、热水器和熨斗运行时的功率需求非常接近，文献［6］方法对这些设备仅进行随机匹配，非常容易出现错误，文献［7］方法在时间上进行就近匹配，仅部分情况能够匹配正确，而本文模体挖掘在匹配时考虑了所有的可能性，采用本文所提方法得到的结果远大于其他方法。在图A3 的REDD_house1 中，台灯是多状态设备，在重叠设备序列中难以进行匹配，并且所有的特征样本在训练时集中在同一个图中，采用文献［6-7］方法时无效特征向量太多，会进一步增大识别难度，导致其他类别设备的识别准确度也略低于本文所提方法。同样地，在图A4 的REDD_house3 中，电视机与冰箱以及微波炉与热水器运行时的功率需求非常接近，且卧室灯和厨房灯是多状态设备，因此文献［6-7］方法对这几类设备的识别准确度也远低于本文所提方法。

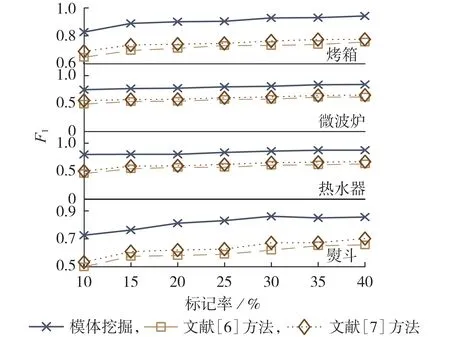
图9 在REDD_house1中3种方法的对比结果Fig.9 Comparison results of three methods in REDD_house1

5.2 基于调和函数的半监督学习算法验证

本节将负荷识别的基于调和函数的半监督学习算法分别与监督类算法中的反向传播BP（Back Propagation）神经网络和k最邻近kNN（k-Nearest Neighbor）法［15］以及无监督类算法中的基于信息熵的模糊聚类算法［14］进行对比。

1）与监督类算法的对比。

监督类算法与半监督类算法均需要部分已标记样本，样本处理及实验过程与5.1节相同。对比结果如图10和附录A 图A5、图A6所示。可以看出：随着标记率的提高，3 种算法的识别准确度均逐渐升高；在样本比例较低时，基于调和函数的半监督学习算法的识别准确度最高，BP 神经网络和kNN 的识别准确度较低；在标记率为35%及以上时，3种算法对部分设备的识别准确度较接近；在标记率为40%及以下时，基于调和函数的半监督学习算法对部分设备的识别准确度始终高于另外2 种算法，这说明本文所提方法的准确度与可推广度更高。

图10 在REDD_house1中3种算法的对比结果Fig.10 Comparison results of three algorithms in REDD_house1

2）与无监督类算法的对比。

无监督类算法理论上不依赖于已标记样本，但是在负荷分类结束后仍需要利用部分信息判断所划分的负荷属于哪一类，因此本节将少量的已标记样本用于识别，并与同样数量样本识别的半监督类算法进行对比。图11 和附录A 图A7 给出了在10%的已标记样本下2 种算法的对比结果，图中设备编号与名称的对应关系见附录A 表A1。可以看出，对大部分设备而言，基于调和函数的半监督学习算法在较少已标记样本的情况下比基于信息熵的模糊聚类算法的准确度高。

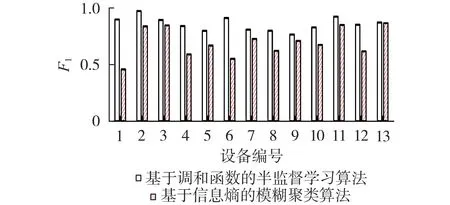
图11 在REDD_house1中2种算法的对比结果Fig.11 Comparison results of two algorithms in REDD_house1

6 结论

减少对人工成本的依赖，是NILM 方法推广应用的关键。本文从实用性角度出发，基于低频采样数据，提出一种基于模体挖掘与调和函数半监督学习的NILM 方法。利用设备运行的基本约束与事件发生的时间逻辑，确定唯一匹配的设备运行窗并建立设备特征库，对不能唯一确定的匹配事件，以模体挖掘法分析所有的可能性。根据不同类型设备开启过程与稳定运行时的差异，采用累积和频数分布等统计方法提取出能反映设备特性的特征量，并通过构建设备运行窗的特征向量，利用基于调和函数的半监督学习算法对设备类型进行识别。从事件匹配和设备识别的角度，将本文所提方法与其他NILM方法进行对比，算例分析结果表明：相比于事件匹配法，本文模体挖掘能够对功率相近的设备和多状态设备进行准确识别；在负荷识别方面，在准确度需求相同时，基于调和函数的半监督学习算法比有监督类算法所需样本标记率低，在低标记率时比无监督和有监督类算法的准确度高。因此，算例测试证明了本文所提方法具有更高的准确度和可推广度。

附录见本刊网络版（http：//www.epae.cn）。