基于自供给模式的电动汽车换电站供需均衡运营策略

代 亮，刘治南，陈天泉，秦 雯

（1. 长安大学电子与控制工程学院，陕西西安 710064；2. 长安大学特殊地区公路工程教育部重点实验室，陕西西安 710064）

0 引言

电动汽车（EV）的发展受到有限的充电时间和充电设施数量的限制。相较而言，以换电模式为EV补充电能的过程较快，且无需停车位的支持，更加集约、高效。通过对电池进行统一管理、集中慢充，不仅能有效保证充电安全性，延长电池的寿命，还能辅助城市电网“削峰填谷”，消纳更多的可再生能源。目前，以换电模式为EV补充电能引起了工业界和学术界的广泛关注［1-2］。将“建设充电桩”扩展为“增加充电桩、换电站等设施”，换电站（BSS）作为新基建的重要组成部分第一次被写入政府工作报告。根据《电动乘用车共享换电站建设规范》团体标准征求意见，未来EV将实现换电系统和电池乃至汽车底盘的共享。工信部已明确指出要将换电站作为新基建重点，大力构建经济便捷的“车电分离”换电服务网络。推广普及换电方案，统一电池规格，广泛地增设换电站是一种具有商业潜力的可行举措。鉴于此，在保证换电站满足EV 用户较高的服务质量水平需求的条件下，如何优化换电站的换电调度策略并根据换电站状态制定提高换电站运营效益的机制是值得探索且亟待解决的热点问题［3-4］。

已有关于EV 充换电调度策略的研究大多以降低换电站的充电成本为优化目标：文献［5］提出了综合考虑EV 充换储一体站与主动配电网的优化调度模型，减少了分布式电源、负荷的预测误差对配电网运行的影响；文献［6］提出了基于柔性致动／评价（SAC）算法的充换电负荷实时优化调度策略，并求解得到并网充换电负荷的实时调度方案；文献［7］提出了基于深度强化学习的换电站模型，采用深度确定性策略梯度确定充电桩的最佳实时充放电功率；文献［8］分析了换电站应投入的最优电池数量，采用近似动态规划（ADP）算法权衡电池成本与换电站的长期运营成本，为提高换电站的运营效益提供了理论基础；文献［9］将充电调度问题表示为一个带约束的马尔可夫决策过程（MDP），并利用标准拉格朗日算法和动态规划算法求解得到最小化单座充换电站充电成本的策略；文献［10］提出了电池需求虚拟队列，利用李雅普诺夫优化框架开发了基于实时需求的动态充电调度算法，最大限度地降低了电池需求队列的积压；文献［11］将换电站最优充电调度问题建模为带约束的马尔可夫决策问题，得到使换电站利润最大化的充电调度策略。上述研究专注于换电站内为EV充换电或为电池充电的调度问题。

已有研究主要关注于如何通过优化充电调度在调整换电站成本的同时满足EV 的换电需求，EV仅作为电池消费者EV-C（EV as a Consumer）。文献［12］研究了EV 电池的交换模式，考虑EV 既可作为EV-C，又可作为电池服务提供者EV-P（EV as a Provider），提出了一种EV 辅助换电站提供换电服务的调度算法，换电站在考虑电价分布和EV到达率的情况下对电池进行充电。

本文在文献［13］的基础上，提出了一种基于自供给模式的EV 换电站供需均衡运营策略。该运营策略针对未来可行的统一化电池规格和EV 换电站自供给模式，设计换电站的动态奖励机制，吸引周边EV 用户充当EV-P 辅助换电站提供换电服务，并利用带约束的马尔可夫决策模型进行建模［14］。通过动态调整给予EV-P 的奖励来激励EV 进行辅助换电，从而在满足换电站服务质量水平约束条件的同时，最大化换电站的运营效益。

1 系统模型

本文所研究的EV 辅助换电站的运营模式如图1 所示。图中：λ为EV-C 的到达率；μ(t)为t时段EV-P 的到达率。换电站包含主换电仓和备用换电仓，备用换电仓内存放了n0块电池，可以利用微电网充放电技术以及物流网配送调度方式，使这n0块电池在任一时段都保持满电状态，以保障换电站能够满足换电需求。本文以主换电仓为研究对象，其内部电池的状态随着EV-C 与EV-P 的到达情况发生变化。为了能够满足EV-C的换电需求，换电站应保证高电量电池的供给，即需保证系统供需平衡。由于调度备用换电仓内电池充电所需的运营和维护成本较大，仅当主换电仓内高电量电池短缺时，才会调度备用换电仓内的电池为EV-C提供换电服务。

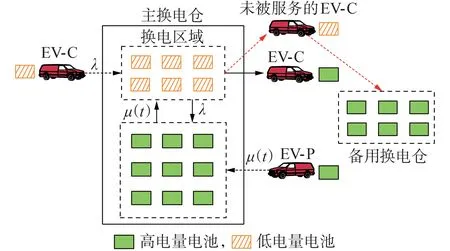
图1 EV辅助换电站的运营模式Fig.1 Operation mode of battery swapping station with EVs’auxiliary

换电站应根据EV-C 的到达情况以及主换电仓内高、低电量电池的数量动态调整给予EV-P 的奖励，激励更多的EV-P 到达换电站以辅助满足EV-C的换电需求。在尽可能不调度备用换电仓内电池提供换电服务的前提下，应在保证换电站服务质量的同时，实现系统平均支出成本最小化。

换电站运营模式的具体描述如下：当在t时段有任意EV 到达换电站时，换电站内的低、高电量电池处于等待调度状态；当在t时段有EV-C 到达换电站时，需根据当前主换电仓内高电量电池的数量调整给予EV-P 的奖励单价c(t)，以刺激EV-P 的到达，即若当前系统中的高电量电池数量较少，则系统会选择为EV-P 提供较高的奖励，以吸引附近更多的EV-P到达换电站进行辅助换电，从而保证系统中存在一定数量的高电量电池，以满足换电站为EV-C提供换电服务的需求。可以看出，换电站在服务质量与运营效益之间存在折中，需要通过动态调整给予EV-P的奖励，制定长期满足用户满意度约束的定价策略，从而在保证换电站服务质量水平的前提下最大化换电站的运营效益。EV 辅助换电站的随机调度模型如附录A 图A1 所示，该模型由换电站内EV-C 的到达状态a(t)、高电量电池队列长度q(t)、给予EV-P的奖励单价c(t)以及EV-P的到达状态b(t)构成。

1.1 EV到达模型

假设EV-C 到达换电站的过程服从参数为λ的伯努利过程［15］，则t时段EV-C 以到达率λ到达换电站的过程可表示为：

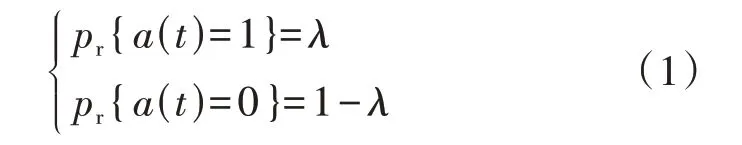
式中：pr{·}为事件{·}发生的概率；a(t)=1 表示t时段有1 辆EV-C 到达换电站进行换电，a(t)=0 表示t时段没有EV-C 到达换电站。式（1）描述了t时段是否有EV-C到达换电站的概率。

同理，假设EV-P到达换电站的过程服从参数为μ(t)的伯努利过程，则t时段EV-P 以到达率μ(t)到达换电站的概率可表示为：

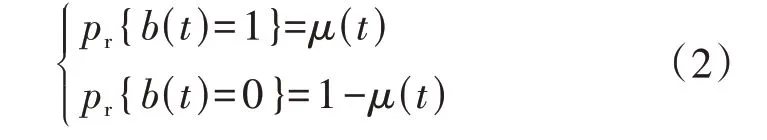
式中：b(t)=1 表示t时段有1 辆EV-P 到达换电站辅助完成换电服务，b(t)=0 表示t时段没有EV-P 到达换电站辅助换电。

1.2 奖励单价状态模型

换电站在t时段给予EV-P 的奖励单价为c(t)，考虑K个可行的奖励单价，则奖励单价状态集合为C={c1，c2，…，cK}，其中ck-1＜ck（k=2，3，…，K）。令μk为给定奖励单价状态ck下EV-P 的到达率，即当奖励单价c(t)=ck时，有μ(t)=μk。同时可以给定一个与之相对应的EV-P 到达率集合B={μ1，μ2，…，μK}。较高的奖励单价会吸引EV-P 以较高的概率到达换电站辅助换电，那么对于任意ck-1＜ck，相应地有μk-1＜μk。且当奖励单价为0时，没有EV-P愿意到达换电站辅助换电，即当ck=0时，有μk=0。

1.3 换电站电池队列状态模型

根据EV 电池的能量水平对EV 用户进行划分：若电池电量高于βEN（0≤β≤1，EN为电池的额定容量），则可认为该电池为满电状态，且相应状态的EV用户（EV-P）在得到令其满意的奖励条件下才会到达换电站辅助换电；若电池电量低于αEN（0≤α≤1），则认为该电池为低电量状态，且相应状态的EV用户在需要进行换电的情况下才会到达换电站进行电池更换；若电池电量处于［αEN，βEN］范围内，则默认EV 不会到达换电站。在本文的调度过程中，主要考虑高电量、低电量这2 种电池状态，且低电量电池的电量为αEN，高电量电池的电量为βEN。

换电站主换电仓内的插槽总数为NS，即共有NS块电池，包括NL块低电量电池和NF块高电量电池，且不论是EV-C 到达换电站还是EV-P 到达换电站，都是将其电池与换电仓插槽内的电池进行交换，因此有NS=NL+NF，NL、NF不断发生变化，而插槽内的电池总数量NS不会发生变化。备用换电仓内的n0块电池可以依靠微电网技术在任何时段开始时都保持为高电量状态，当且仅当t时段主换电仓内的高电量电池数量NF无法满足换电需求时，才会利用备用换电仓内的备用电池，即2 个换电仓的电池使用状态存在优先级，且备用换电仓内电池的状态不随时段变化而发生变化。因此，只需研究主换电仓内某一种电池状态队列的变化情况即可，另一种状态电池的数量可利用NS=NL+NF间接求得。换电站主要向EV-C 提供换电服务，且EV-C 所需的电池为高电量电池，因此本文以高电量电池的数量NF为研究对象。考虑EV-C 与EV-P 之间的独立性，即EV-C 与EV-P 不能避开换电站独立完成电池交换。在t时段，若有车辆到达换电站，首先观察主换电仓插槽内是否有相应的电池为到达车辆提供换电服务。假设t时段到达换电站的车辆为EV-C，且高电量电池的数量NF=0，此时即使有EV-P 到达换电站，换电站也无法用主换电仓内的电池为EV-C提供换电服务，因此该换电站面向EV-C的服务质量会降低。

由于换电站主换电仓插槽内的高电量电池数量NF随着EV-C 与EV-P 的到达情况动态变化，将NF建模为随时段动态变化的电池队列长度q(t)。t时段至t+1时段，高电量电池队列长度的更新表达式为：

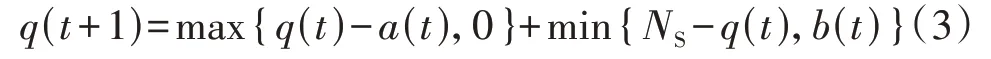
式中：q(t+1)为t+1时段高电量电池队列长度。

1.4 系统服务质量模型

本文考虑服务质量约束条件下换电站支出成本最小化问题，当EV-C 到达换电站时，若主换电仓内的高电量电池数量无法满足其换电需求，考虑到备用换电仓内电池所需的运营和维护成本较大，为了保证换电站的主换电仓与备用换电仓具有同样的利润，则换电站为备用换电仓内电池设定更高的定价，此时EV-C必须支付更高的费用才能完成换电，从而导致EV-C 的满意度降低。本文研究选择不同的定价激励EV-P到达换电站辅助换电的最优化问题，以主换电仓内的电池为研究对象，以最大化主换电仓的运营净利润为优化目标。此时，换电站的服务质量水平可用t时段主换电仓无法为EV-C提供换电服务的电池数量l(t)衡量，具体表达式为：

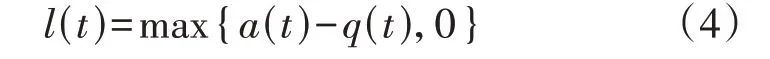
1.5 动态定价策略模型

最优定价策略存在如下决定性因素：t时段换电站主换电仓插槽内高电量电池数量NF，即当前高电量电池队列长度q(t)。换电站的决策变量为系统处于状态q(t)时换电站给予EV-P 的奖励单价。给定如下概率集：{f k i}∈{0，1}（0≤i≤NS，k∈{1，2，…，K}），i为高电量电池数量，即q(t)=i；f k i为当q(t-1)=i时，选择给予EV-P的奖励单价为ck的概率，见式（5）。

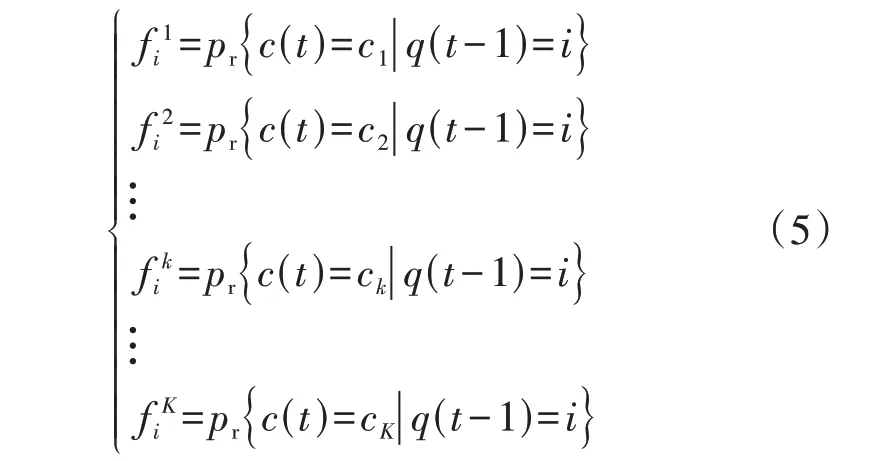
假设当换电站内高电量电池数量足够时，可以选择不给予EV-P任何奖励，使其不会到达换电站辅助换电。因此c1的取值可以为0，因此ck∈[0，M]，M的取值取决于换电站因建设及运营成本限制所能提供给予EV-P的最大奖励单价。

2 优化问题

2.1 优化问题构建

本节分析在EV-C 损失率约束条件下最小化换电站支出成本的优化问题。

式中：πi为状态q(t)=i下系统的稳态概率。

2.2 优化问题的求解

由最优化理论可知，对于线性问题式（9），一定存在唯一最优解。在得到该线性规划问题的最优解后，对应的稳态概率可以表示为：

3 优化方法

本节基于EV-P 辅助换电的换电站系统最优定价选择过程，构建带约束的马尔可夫决策框架。考虑到换电站的电池数量具有随机性，在保证换电站满足服务评价标准服务质量的条件下，以最小化换电站支出成本为目标，建立优化问题进行分析。

3.1 马尔可夫决策框架

MDP 一般由五要素构成，为了得到换电站的最优定价选择策略，建立一个包含五元组的MDP 模型，包括决策时间序列TS∈R（表示进行连续决策的时段）、t时段高电量电池队列长度q(t)、t时段为实现优化目标所选取的给予EV-P的奖励单价、决策周期长度τ以及各时段的决策变量。根据1.3 节所述内容，给予EV-P 的奖励单价ck会有一个与之相对应的EV-P 到达率μk。由于单位时段内EV-P 的到达率μk会对系统的高电量电池队列长度q(t)产生直接的影响，在构建马尔可夫决策框架时可以用EV-P 的到达率等效奖励单价的动态选择。所构建的换电站最优定价选择模型可用(Q，A，B，H，Cˉave)表示，其中Q={0(NS)，1(NS-1)，···，i(NS-j)，···，NS(0)}为不同时段换电站主换电仓插槽内高电量电池（低电量电池）的队列长度（NF=i(NL=j)为系统状态）；A={a(t)|a(t)∈{0，1}}表示EV-C 的到达情况，表明系统的不确定性；B∈{μ1，μ2，…，μK}为换电站在该时段所执行的动作集合，即给予EV-P的动态奖励单价所对应的EV-P到达率的集合，在每个时段换电站根据高电量电池队列长度q(t)做出决策；H为状态转移概率矩阵，其元素τi，j为系统中高电量电池数量由i变为j的状态转移概率；Cˉave为马尔可夫决策框架中的奖励，表示换电站为了满足供需平衡，通过价格吸引EV-P 到达换电站辅助换电所提供的奖励。下文采用马尔可夫链对系统内高电量电池队列的转移概率进行描述，在给定换电站EV-C损失率的约束条件下，通过动态定价策略对给予EV-P 的奖励Cˉave进行分析，求解换电站平均支出成本最小化问题。

3.2 马尔可夫链模型

换电站内高电量电池队列状态的马尔可夫链模型见附录A 图A2。t时段至t+1时段，高电量电池数量由i变为j的状态转移概率τi，j可表示为：

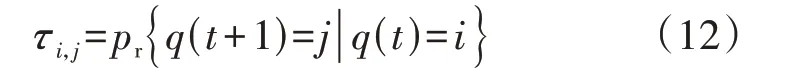
令p(i，j)={τi，j}为系统状态空间的状态转移概率，由MDP 的性质可知系统状态转移与t时段无相关关系，因此可以将变量的标注t省略，则EV-C 与EV-P 到达状态(a(t)，b(t))可用(a，b)表示状态间的转移方式。状态Q无法在下一个时段中转换到与其没有链接的状态。当系统状态为0 时，若有EV-C 到达，则主换电仓无法为该用户提供换电服务，会降低用户的满意度，导致服务质量水平降低。每个时段状态之间的转移可以分为3 种情况，分别见附录A式（A1）—（A3）。

换电站的状态转移概率矩阵H可表示为：

定义π=[π0，π1，…，πNS]为换电站状态的MDP稳态概率矩阵，根据马尔可夫链性质，可由式（14）求得。

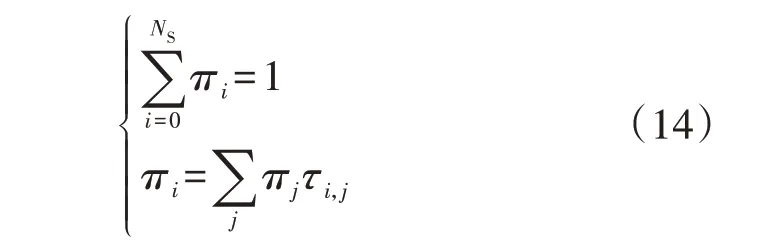
3.3 基于服务质量约束的马尔可夫决策框架模型

在得到系统处于各状态的稳态概率后，系统在状态q(t)=i下损失的EV-C 数量将影响系统的服务质量水平，因此根据t时段系统所处状态q(t)=i、给定的服务质量模型及该状态下给予EV-P 的奖励单价ck，换电站没能提供换电服务的EV-C 数量，即t时段EV-C损失数量的期望可表示为：

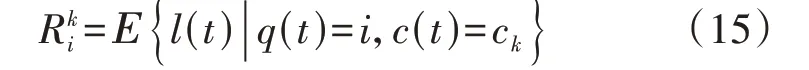
式中：Ε{·}表示数学期望。

由本文构建的马尔可夫链模型可知，系统仅在状态i=0时，才会造成EV-C损失，其概率ο0可表示为：

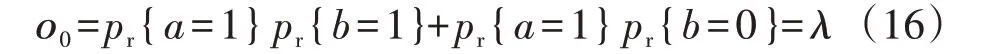
t时段系统的EV-C 损失量为l(t)=max{a(t)-q(t)，0}。因此在给定给予EV-P 的奖励单价ck时，t时段EV-C损失数量的期望可进一步表示为：

4 算例仿真分析

4.1 算例参数设定

本文基于EV-P辅助换电场景，提出了一种动态最优定价策略，通过算例仿真对其进行验证。算例仿真相关参数及动态定价参数和EV-P 到达率分别见附录B表B1和表B2。

结合上述参数，采用线性规划方法求解优化问题可获得使换电站支出成本最小化的最优动态定价策略。为了验证本文所提动态定价策略在保证系统服务质量水平的基础上更好地节约了支出成本，分两部分进行仿真分析：①针对模型性能，验证不同EV-C损失率阈值限制下换电站支出成本的变化情况、不同EV-C 到达率λ下换电站支出成本的变化规律；②对比本文所提动态定价策略与固定定价策略。

4.2 模型性能分析

系统净利润为换电站通过为EV-C 提供换电服务所得收益与给予EV-P 换电奖励的支出成本及为备用仓电池充电的支出成本之差。考虑到换电站的口碑问题，防止因换电站对EV-C提供换电价格波动导致的用户流失，将为EV-C提供换电服务的价格设为定值（参考蔚来汽车换电站的收费方式，设定为EV-C 提供换电服务所得收入=换电电量×（电价+服务费））。本文所得每种EV-C 到达率λ下的最优解可以使给予EV-P换电奖励的支出成本最小化的同时降低EV-C 损失量，当EV-P 不能满足EV-C 的换电需求时，动用备用电池仓内的电池以满足换电服务，提高了备用电池仓的成本，参考电池容量为150 kW·h，工商用电电价为0.7元／（kW·h），备用仓电池的充电成本为(λ-μ)×150×0.7，换电站为EV-C提供换电服务所得收入为150×(1.35+0.39)×λ。

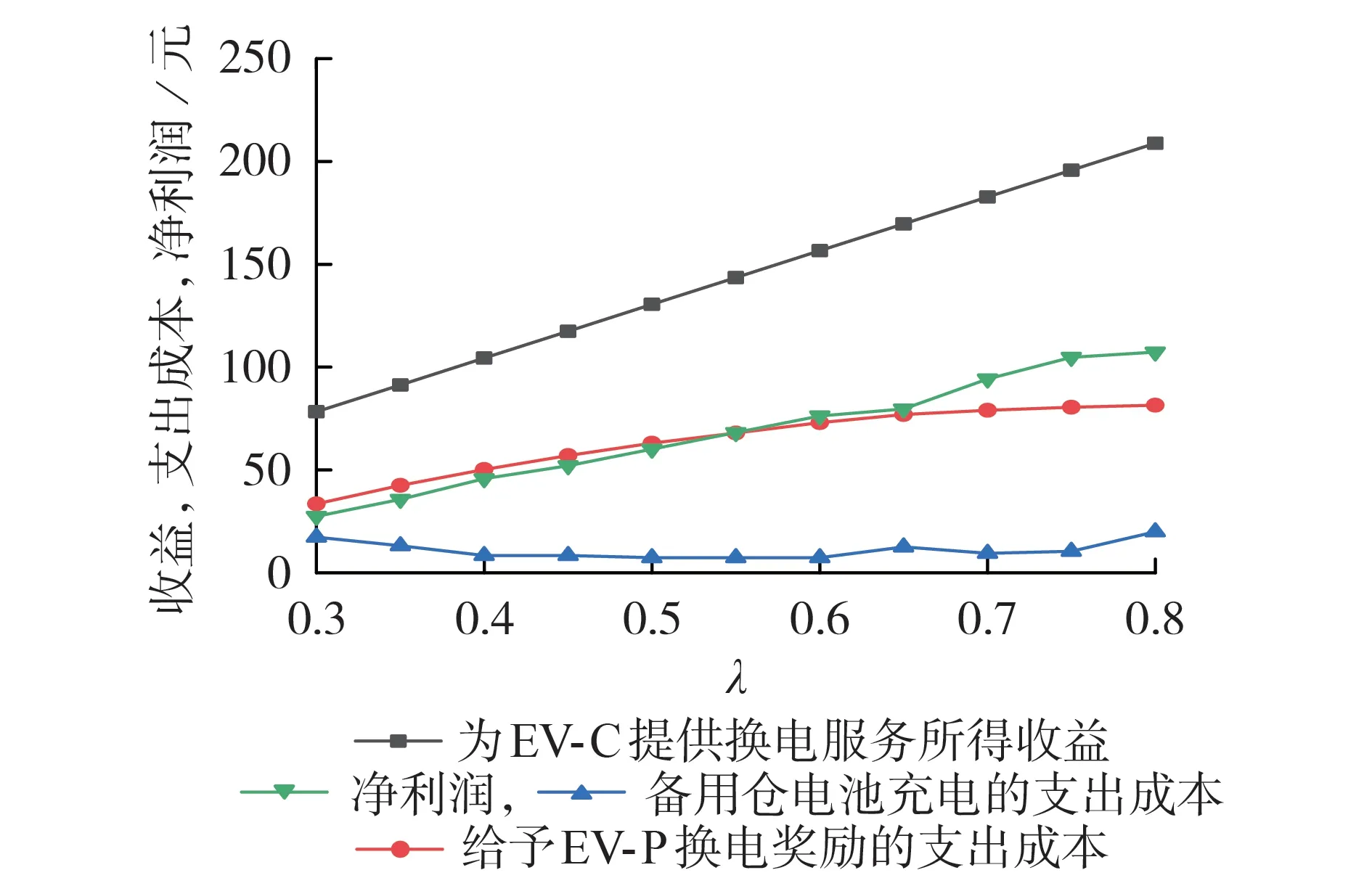
图2 不同EV-C到达率下换电站系统的收益与支出成本变化曲线Fig.2 Income and cost curves of battery swapping station system under different arrival rates of EV-C

服务质量和系统净利润之间存在一个折中，在系统EV-C到达率比较稳定的情况下，服务质量和系统净利润之间的关系可以用EV-C损失率与系统给予EV-P 换电奖励的支出成本之间的关系表示，如附录B 图B1 所示。由图可知：在给定EV-C 到达率λ=0.7的条件下，随着系统给予EV-P换电奖励的支出成本的减少，EV-C 损失率增大，即换电站的服务质量下降，此时不需要过多的EV-P到达换电站。因此系统可以选择以较低的定价吸引EV-P 以较低的概率到达换电站辅助换电，从而降低系统的总支出成本。在实际的应用中，可根据特定场景下不同的服务质量需求调整支出成本。

4.3 不同策略对比分析

给定EV-C 到达率λ=0.7，本文所提动态定价策略与固定定价策略下的换电站平均支出成本结果见附录B 图B1。由图可知：随着EV-C 损失率阈值减小，即在保证系统提供更高的服务质量水平要求下，动态定价策略与固定定价策略下换电站的平均支出成本都增大；当换电站的平均支出成本足够大，即能吸引更多的EV-P 到达换电站辅助换电时，2 种策略下的EV-C损失率都降至最低；对于任意给定的EV-C损失率阈值，固定定价策略下的换电站平均支出成本始终高于动态定价策略。上述结果验证了动态定价策略能在保证服务质量水平的同时，减少换电站支出成本，为换电站带来更多的盈利机会。

5 结论

本文针对自供给模式EV 换电站的供需平衡问题，提出了一种动态定价策略，利用动态定价机制调整辅助换电EV的到达率，从而保证换电站内高电量电池数量需求得以满足。在未来EV 电池统一规格以及电网峰谷分时定价的背景下，EV 用户可作为EV-P，通过赚取电池充电过程的差价盈利；换电站通过动态调整给予EV-P的奖励来减少支出成本。所提策略既能满足换电站对高电量电池数量的需求，也有助于城市电网“削峰填谷”；同时慢充可以有效保证充电安全与电池寿命，EV-P也可以从中获利。

附录见本刊网络版（http：//www.epae.cn）。