计及源荷不确定性及频率安全的电力系统区间优化调度方法

宋晓芳，周海强，薛 峰，高 超，赵春祝，颜云松

（1. 智能电网保护和运行控制国家重点实验室，江苏南京 211106；2. 国电南瑞科技股份有限公司，江苏南京 211106；3. 河海大学能源与电气学院，江苏南京 210098）

0 引言

为了建设新型电力系统，我国电力系统中风电、光伏等新能源占比不断提高。以风电为例，截至2020 年底，我国风电累计装机容量已达到2.8×108kW，风力发电占总发电量的12.79%，而且这一比例还将持续增长［1］。风电具有间歇性、波动性和随机性，大规模风电的接入加剧了电力系统源侧的不确定性。在荷侧，负荷不可避免地存在一定预测误差，近年来，需求响应DR（Demand Response）负荷被大量推广，其中价格型DR 受到电价、气温、消费心理等多重因素的影响，其响应数量及负荷转移的目标时段均具有一定的随机性，从而加剧了荷侧的不确定性。因此，源荷双侧的强不确定性是新型电力系统调控所必须考虑的问题。

随着新能源占比的逐步提高，传统同步机组占比不断下降，系统惯量水平降低，调频能力减弱，频率安全问题凸显［2］。英国、澳大利亚等国都曾发生过系统惯量偏低导致频率快速跌落从而诱发连锁故障的事故［3］，而源荷不确定性又进一步增加了系统的频率安全风险。因此，频率安全问题是新型电力系统调控所必须考虑的另一个重要问题。

国内外学者对计及不确定性的调度问题进行了大量研究，目前常用的主要有场景法［4］、机会约束规划CCP（Chance Constrained Programming）方法［5］、鲁棒优化方法［6-7］、区间优化方法［8-9］等。场景法通过抽样生成大量场景来模拟不确定性，需要知道变量的概率分布，且计算量较大，对于大型电力系统而言往往难以实施［4］。CCP 方法在一定置信水平内进行决策，文献［5］在考虑新能源及负荷不确定性的条件下应用CCP 方法研究了电网优化调度问题。但由于CCP 方法需要通过卷积求取多个随机变量的联合概率密度分布函数，往往难以实现，故一般只限于高斯分布等特殊情况。鲁棒优化方法针对不确定性参数的最劣取值情况进行最优决策，不需要随机变量的概率分布信息，计算量小，但结果较为保守。为了抑制解的保守性，鲁棒优化方法［6-7］常通过盒式或多面体不确定集等对最劣场景的覆盖范围加以控制，从而在安全性和经济性之间取得一定平衡。区间优化方法以区间数的形式来描述随机变量，对不确定变量信息要求低，计算量小，但与鲁棒优化方法相类似，区间优化方法基于最劣场景进行决策，其结果一般偏于保守［8-9］。文献［9］应用区间优化方法研究了机组组合问题，通过对所有场景的分析挑选出最劣场景，在此基础上进行调度决策。由于实际系统中往往难以确知源、荷变量的概率分布，因此，基于概率的调度方法存在不少困难，而区间优化方法则可以较好地解决这一问题。

传统电力系统的动态频率安全一般通过安全稳定控制来保障，调度过程中对此考虑较少，但对于高比例新能源电力系统，频率安全问题日益突出。如果运行方案不合理，将会增大频率失稳的风险。近年来，不少学者对计及频率安全的调度问题进行了研究。文献［10］对考虑频率安全的电力系统优化问题进行了综述，对频率安全特性分析、多类型频率响应、频率安全约束的构造等问题进行了阐述。文献［11］研究了考虑安全约束的机组组合问题，为求解含频率安全约束的混合整数规划问题，应用分段线性化方法将最低频率的表达式转换为线性方程，从而克服了非线性频率安全约束所带来的求解困难。文献［12］应用场景法研究了大规模风电参与调频条件下的机组组合问题，文中采用时域仿真方法对动态频率安全进行校验，若频率安全约束得不到满足，则根据频率响应机理对机组出力和系统惯量进行调节。但该方法依赖于对大量场景的暂态仿真计算，计算量较大。总体而言，在调度问题中考虑频率安全约束的主要困难在于系统频率响应是一个复杂的非线性曲线，它与机组运行状态、输出功率等密切相关，如何处理非线性频率安全约束仍然是有待研究的一个问题。

针对以上问题，本文提出了一种计及源荷不确定性及频率安全的电力系统区间优化调度方法。首先，对电力系统频率响应进行分析，推导了描述频率安全约束的近似线性不等式；然后，建立了计及频率安全的电力系统区间优化调度问题数学模型，应用Benders 分解方法求解区间优化问题，将原问题分解为基准场景下的主问题和不确定性场景下的可行性校验子问题；进一步地，为减少待校验场景的数量，基于风险指标筛选出少量高风险场景，对其进行分析；最后，将所提方法应用于含风电的10 机39 节点算例系统，验证了其安全性和经济性。

1 电力系统的频率安全约束

当系统遭受如负荷突增、机组跳闸等扰动时，同步发电机转速下降，系统频率会发生如图1 所示的波动过程。图中：Δf为频率偏差；tm为频率最低点对应的时间；Δfm为tm时的频率偏差。

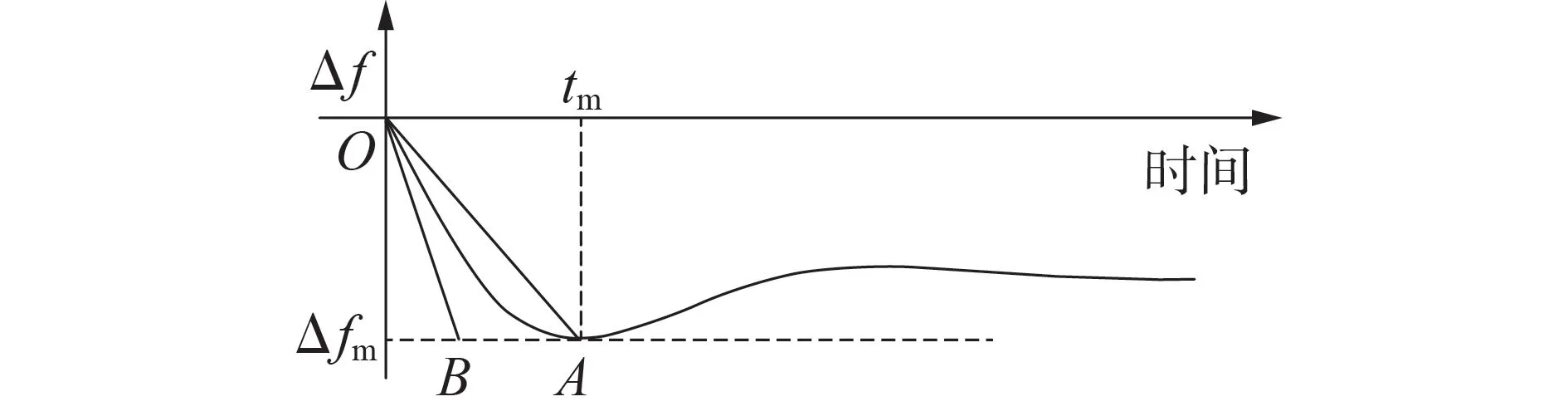
图1 动态频率响应曲线Fig.1 Dynamical frequency response curve

频率动态响应过程可由以下方程描述：

式中：M为系统惯量；ΔPm为机组机械功率增量；Dg为发电机阻尼系数；ΔPo为故障引起的功率缺额；PL，0为额定频率时的负荷功率；kLf为负荷的频率特性系数；D=Dg+PL，0kLf。ΔPm与频率偏差Δf的关系为：

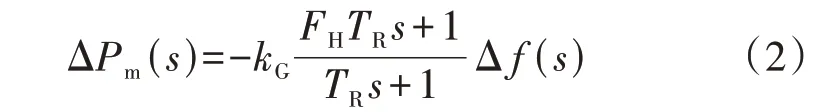
式中：kG、FH和TR分别为调速器增益、再热器系数和再热器时间常数。

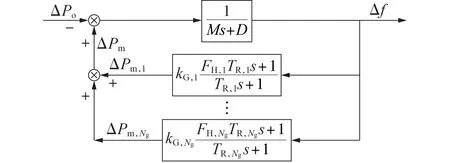
图2 平均系统频率响应模型Fig.2 ASF model

频率安全约束要求f(tm)≥fcr，其中fcr为系统允许的频率最低值。由于f(tm)是一个复杂的非线性函数［11］，要纳入混合整数规划问题进行求解存在困难，为此需要对频率安全约束进行近似化简［14］。如果f(tm)＜fcr，则表明系统需要比Δfcr更大的频率跌落量才能实现功率平衡，此时不满足频率安全约束。因此，频率安全约束等价于频率偏差为Δfcr时，调频功率大于或等于功率缺额。

图1 中kOB=-ΔPo/M，因此kOA=-2ΔPo/(πM)，若最大频率偏差为Δfcr，则频率最低点对应的时间为：

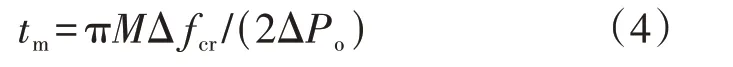
在已知Δf(s)的条件下可根据式（2）求出ΔPm。由于Δf(s)的计算较为复杂，为简化计算，可用直线OA来近似Δf(t)，将Δf(s)=-kOA/s2代入式（2），求其Laplace 反变换可得发电机Gi在频率最低点的调频功率为：

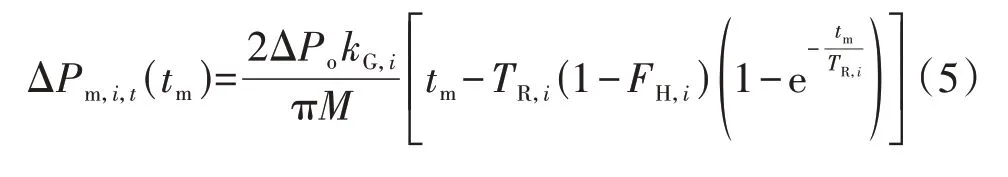
式中：Pi，max为发电机Gi出力的上限。

因此，系统频率安全约束方程为：

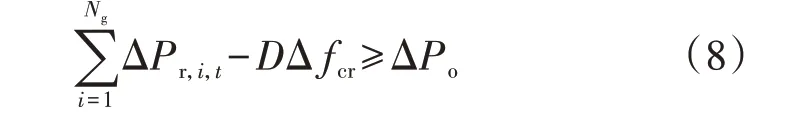
由式（6）—（8）可以看到，除了调差系数等发电机本体参数以外，频率安全约束方程式（8）还受到决策变量ui，t、Pi，t的影响，调度中心可通过改变发电机开停机状态或调整发电机出力来改变系统整体的可用调频功率。

2 计及频率安全的区间优化调度问题

假设风电及负荷的预测值是已知的，其不确定性通过预测误差的波动区间来表示。以日综合运行费用为目标函数，可构建区间优化调度问题的数学模型。目标函数F包括3 个部分，即机组运行费用、弃风费用以及负荷调控费用，其表达式如下：

式（9）—（19）构成了含区间不确定变量的优化调度问题数学模型。如果以源荷功率预测值为基准场景，由于实际场景与基准场景不可避免存在偏差，运行时需要根据实际场景对预先设定的运行方案不断进行修正，以确保调度方案的可行性和经济性。因此，区间优化调度的目标是求出基准场景下的优化调度方案，并确保从该方案出发，对于任意场景均存在可行的校正调度方案。

3 基于Benders 分解及高风险场景集的求解方法

对于不确定性场景，需要在基准方案的基础上进一步修正。基于Benders分解方法，原问题可以分解为基准场景下的主问题以及不确定场景下的可行性校验子问题［8，17］，有关原问题分解的原理详见附录A，以下分别对其数学模型及求解方法加以说明。

3.1 基准场景下的主问题

为简明起见，下文以下标f表示不确定变量的预测值，设风电出力预测值和负荷功率预测值分别为Pw，j，t，f和Pl，k，t，f，则基准场景下的主问题见式（20）。

主问题的目标函数包括基准场景下的机组运行费用、弃风费用以及负荷调控费用。约束条件包括基准场景下的功率平衡约束、系统备用约束、线路潮流约束以及频率安全约束，gcut(ui，t，Pi，t，rj，t，ρk，t)≤0为可行性校验子问题所返回的Benders割约束。此外，还包括式（12）—（14）中的最小启停时间、机组出力和爬坡约束等。

3.2 不确定场景下的可行性校验子问题

通过求解问题式（20）可获得基准调度方案，校验其可行性即确保在不确定场景下存在可行的校正调度方案，以消除可能存在的违反安全约束的现象。由于场景数量庞大，逐个校验显然不具有可操作性。为此，本文提出了生成高风险场景集并对其进行校验的方法。

3.2.1 高风险场景集的生成

当实际场景偏离基准场景时，如果仍然采取基准调度方案，则系统将发生违反有关功率平衡、备用、线路潮流或调频功率等安全约束的现象。一般而言，该场景下违约程度越严重，通过校正调度消除不安全现象的难度越大，系统发生安全风险的可能性越大，因此，可将此类场景称为高风险场景，并重点对其校正调度方案进行校验。

式中：S为风电及负荷波动生成的所有场景的集合；q1、q2、q3为0-1 变量，其不同组合对应着不同的风险指标h。式（24）的解为高风险场景，不同h所求得的场景总和构成了高风险场景集E。

需要说明的是，大型电力系统线路众多，每条线路均可求出使其潮流越限量最大的高风险场景，为了减少E所包含的场景数量，可选取其中负载率较高的若干线路进行分析，即认为场景变化时重载线路的风险较大。

3.2.2 校正调度的可行性校验

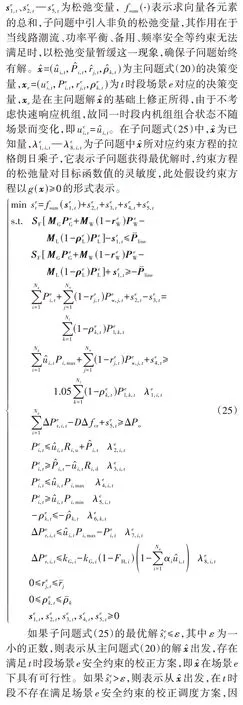
求解区间优化调度问题的流程如图3 所示。图中：Ne为E包含的高风险场景总数；ke为可行性校验的次数。

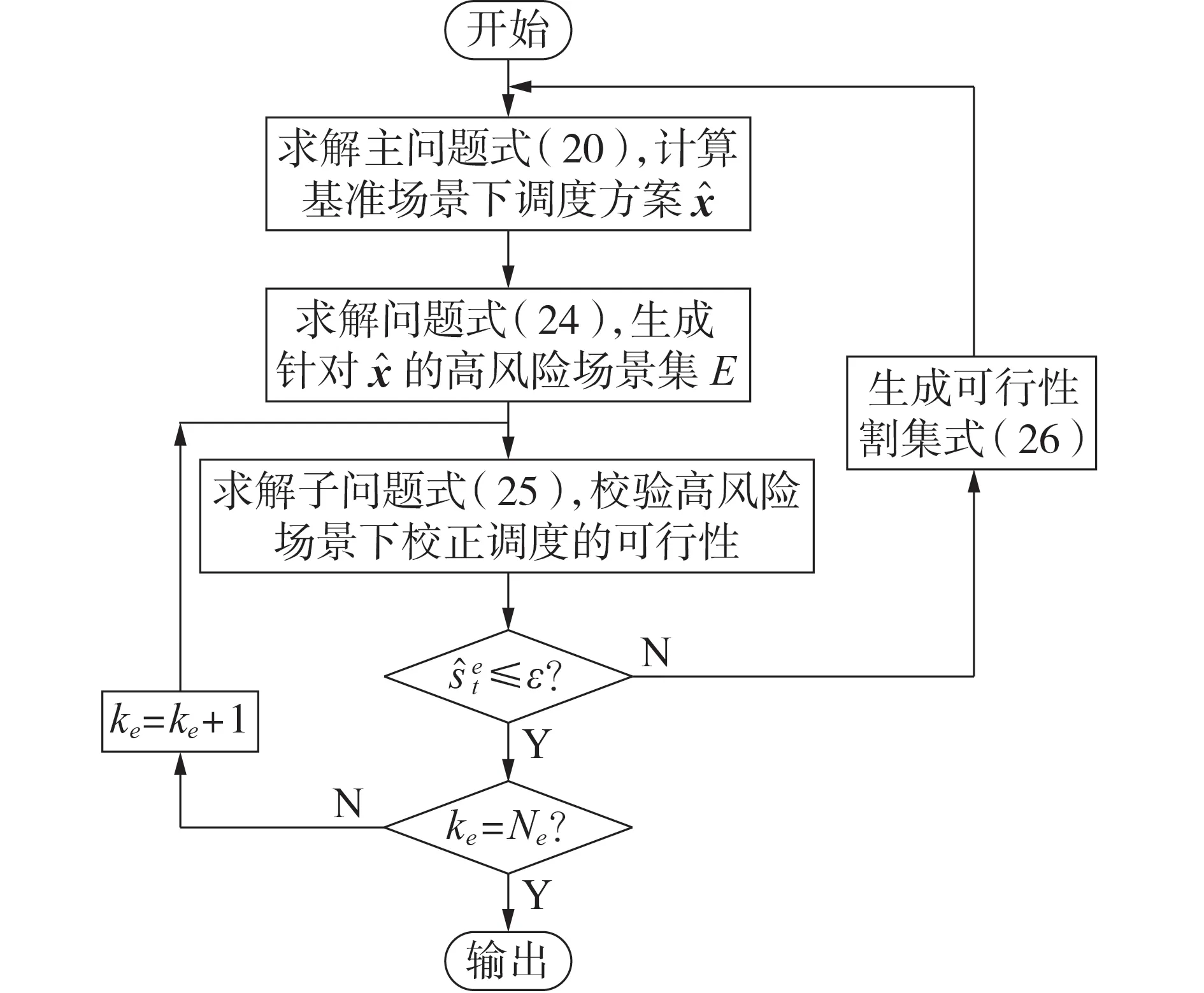
图3 求解区间优化调度问题流程图Fig.3 Flowchart of solving interval optimal dispatching problem

4 算例

为了验证所提区间优化调度方法的有效性，对修改后的10 机39 节点算例系统进行了仿真计算。算例系统结构如附录B 图B1 所示，发电机运行费用、启停成本、爬坡功率、极限功率、最小运行或停机时间等参数如附录B 表B1 所示，调速器参数如附录B 表B2 所示，线路传输功率上限见附录B 表B3。为研究风电不确定性对调度方案的影响，将节点32、33 和35 处的同步发电机替换为3 个风电场W1、W2和W3，未来24 h 风电出力和负荷功率预测曲线分别如附录C 图C1、C2 所示，设风电出力预测误差波动区间均为［-15%，15%］，负荷功率预测误差的波动区间为［-10%，10%］。

4.1 区间优化调度方案分析

考虑到在极端场景下，为了功率平衡可能需要少量弃风。而在负荷高峰时段，削减部分需求响应负荷也是一种较为常用的调控措施，故系统设置了弃风率和减负荷率。取弃风率上限rˉj为0.3，减负荷率上限ρˉk为0.3，cw为105$／MW，cl为185$／MW，fcr=49.5 Hz。设预想故障为负荷突增500 MW，使用GAMS24.7软件对系统调度方案进行了计算。

针对实际场景的调度方案由基准方案和校正方案两部分构成，实际场景具有不确定性，其对应的校正方案也各不相同。基准方案下发电机出力如附录D 图D1 所示，在基准场景下系统没有弃风及减负荷操作，基准方案的总运行费用为$1412644。

为了验证调度方案的频率安全性，以基准方案为例，假设14:00—15:00 时段负荷突增500 MW，对系统频率响应进行了计算，其频率响应曲线如图4所示，频率最低值为49.542 Hz，满足频率安全约束要求。为了观察频率安全约束对调度方案的影响，在不考虑频率安全约束的条件下对区间优化调度方案重新进行了计算，此时运行费用为$1 410 949，与考虑频率安全约束的调度方案相比，降低了0.12%。由图4可见，此时频率响应曲线的最低值为49.368 Hz，低于fcr。由此可见，频率安全约束有效地保障了调度方案下系统的频率安全。

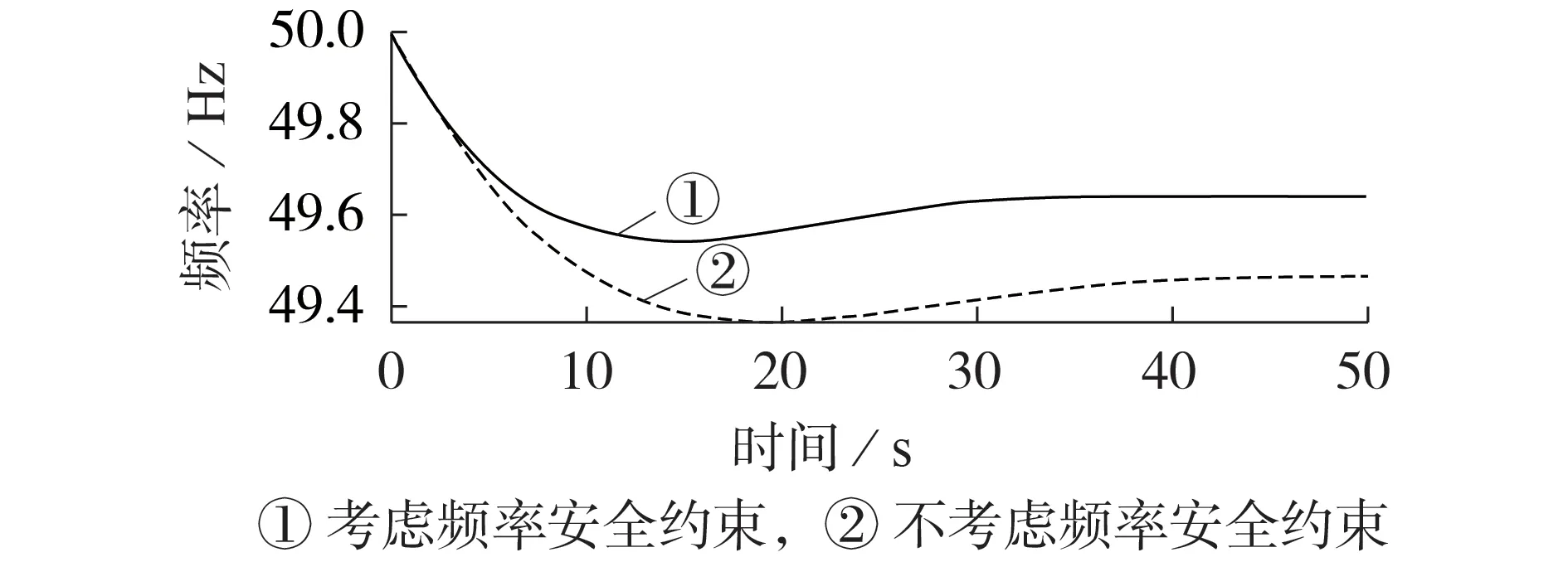
图4 预想故障下不同调度方案的频率响应曲线对比Fig.4 Comparison of frequency response curves between different dispatching schemes under expected fault

图5 给出了考虑、不考虑频率安全约束时发电机G7和G10的出力。

图5 考虑、不考虑频率安全约束时G7和G10的出力Fig.5 Power generations of G7 and G10 with and without considering frequency security constraint

由图5 可以看到，在不考虑频率安全约束的情况下，在13:00—14:00 的负荷高峰时段G7处于满发状态，而G10则留有一定余量，这是由于G7发电成本相对较低，其满发有利于降低系统运行成本。但在考虑频率安全约束时，计算表明，G10能够提供的调频功率受ΔPm，i，t制约，约为64.7 MW。若G7仍然满发，其调频功率为0。在考虑频率安全约束的条件下，调度方案将G7的发电量减小了121.9 MW，使其在故障时可以提供一定的调频功率。此时，尽管G10出力有所增加，但其调频功率仍等于ΔPm，i，t，故系统总调频功率有所提升。但为了满足频率安全约束，系统运行成本也略有增加。

为了验证基准方案在各种不确定性场景下校正调度的可行性，以一种小概率极端场景S1=(P-w，j，t，P+l，k，t)为例进行了计算。与基准场景相比，在13:00—14:00时段存在741 MW的功率缺额，为了平衡功率，考虑发电机增发或减负荷2种措施。但由于从基准方案出发，发电机出力的修正量受到爬坡功率和调频备用的制约，其调节范围难以满足极端场景S1下的需要，故系统采取了减负荷操作，此时运行费用增加到$3091343，负荷功率削减量如图6所示。

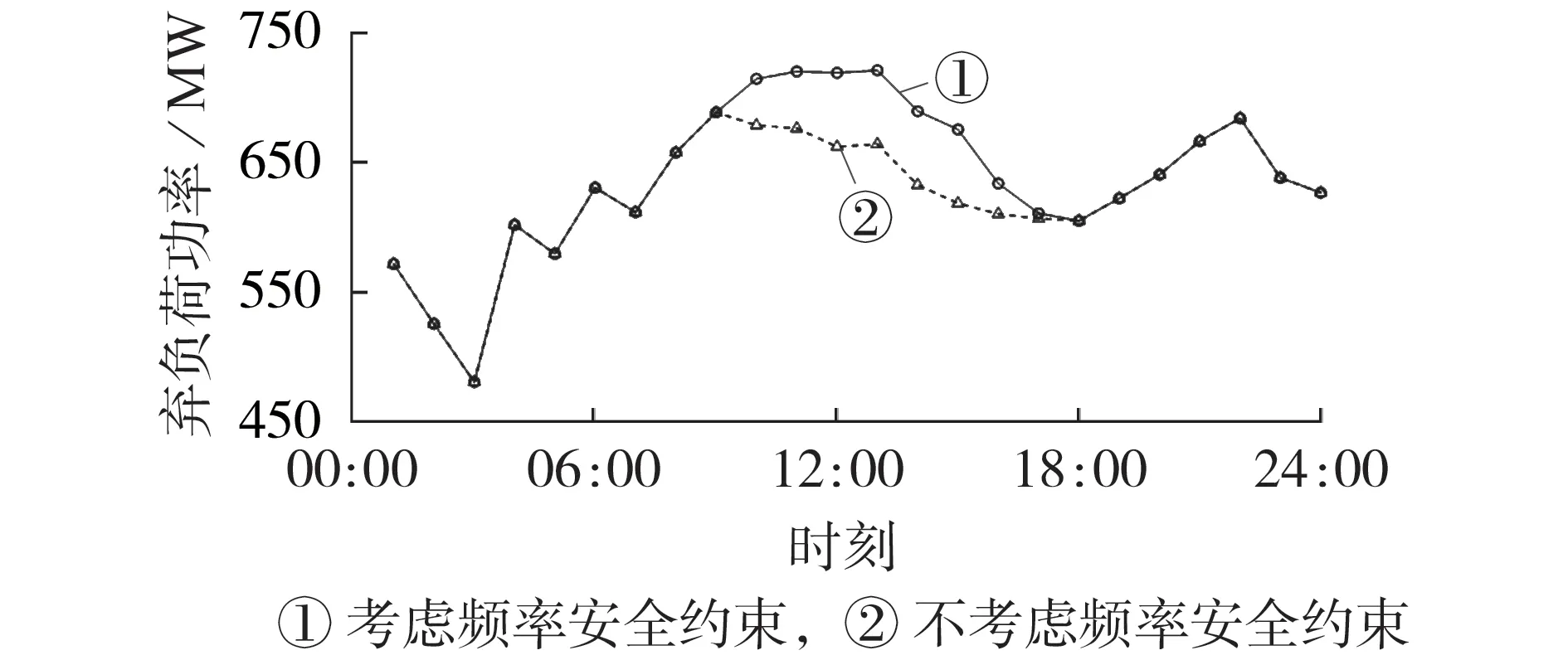
图6 场景S1下的负荷削减量Fig.6 Load shedding amount in Scenario S1

由图6 可见，在不考虑频率安全约束的情况下，负荷削减量会有一定的减少。需要说明的是，上述减负荷措施是针对小概率的极端场景。此时，如果不采用减负荷措施，则需要在系统中加装更多的同步发电机以满足极端场景下的调峰和调频需求，这将会大幅降低系统运行的经济性。

4.2 风电占比及误差波动范围对调度方案的影响

为了研究风电占比对调度方案的影响，将节点33处的风电场W2替换为1台容量为800 MW 的同步发电机，此时风电占比由38.15%降低至26.10%，对区间优化调度方案进行了计算。结果表明，此时系统运行费用增加了15.5%，达到$1 631 627，这主要是由于同步发电机承担了更多的负荷，故运行成本有较大增加。

假定13:00—14:00时段负荷突增500 MW，对不同风电占比下的频率响应曲线进行了计算，结果如附录D 图D2所示。可以看到，由于调度方案考虑了频率安全约束，故不同占比下均能够满足频率安全要求。当风电占比为26.10%时，系统惯量有所增大，故频率的初始变化率有所减小，且频率最低值略大。

为了分析风电预测误差波动范围的大小对调度方案的影响，分别设误差波动范围为±13%、±15%、±17%、±19%，对系统区间优化调度方案的系统运行成本进行计算，表1 给出了不同误差波动范围下调度方案的系统运行成本对比。可以看到，随着预测误差波动范围的加大，基准场景下系统运行成本变化较小，但极端场景S1下系统运行成本显著增长。当误差波动范围由±13%增大至±19%时，极端场景S1下系统运行成本增加了13.26%。

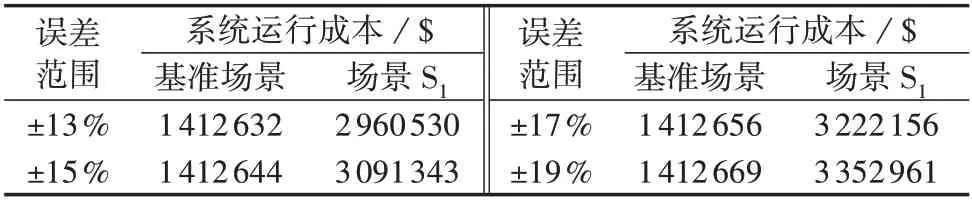
表1 不同预测误差波动范围下调度方案的系统运行成本Table 1 Operation costs of dispatching schemes under different fluctuation ranges of prediction error

4.3 区间优化法与其他方法的对比

为了评估区间优化方法的性能，将其与场景法和CCP方法进行了对比。由于场景法和CCP方法需要知道不确定参量的概率分布，故假设风电及负荷功率预测误差在给定的波动区间内服从高斯分布。

对于场景法，采用拉丁超立方抽样方法并应用同步回代消除法进行场景缩减，生成100 个典型场景，构成场景集A。以上标s表示场景s下的变量取值。设每个场景发生的概率为ps，以Ns个场景运行费用的期望值最小为目标函数，考虑每个场景下功率平衡、线路潮流、频率安全、备用等约束，求解以下的优化问题：

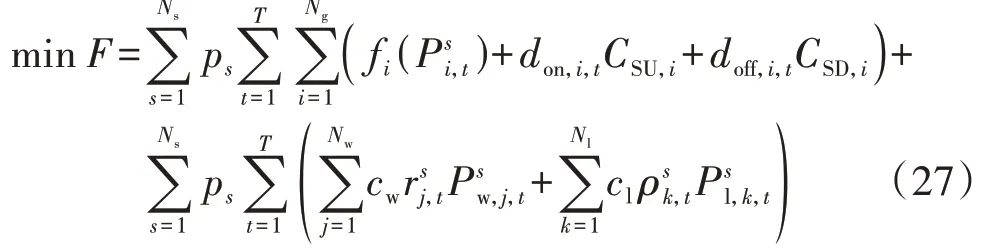
场景法与区间优化方法的对比见表2。由表可知，场景法所得运行费用的期望值为$1 374 366，低于区间优化方法中基准方场景及极端场景S1所需的运行费用。需要指出的是，场景法的优化结果受到场景数量和场景代表性的影响，在生成场景集A时，一些小概率、高风险的场景有可能被遗漏，从而影响调度方案的安全性。而区间优化法通过不同的风险指标，筛选出高风险场景集E，以确保调度方案的安全性，但由于需要兼顾极端场景，故其相对保守。

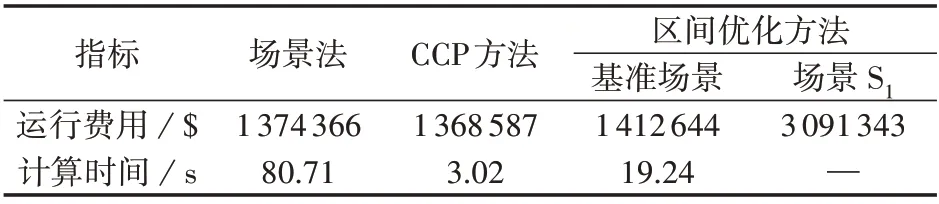
表2 区间优化方法与场景法、CCP方法的对比Table 2 Comparison among interval optimization method，scenario-based method and CCP method

由表2 还可以看到，场景法计算时间为80.71 s，远大于区间优化方法所需的19.24 s，这是由于区间优化方法只需要对高风险场景集E进行分析，而场景法需要对场景集A中的所有场景进行分析，故区间优化方法计算量较小，具有较快的计算速度。

对于CCP方法，优化调度问题数学模型为：

5 结论

本文提出了一种计及源荷不确定性及频率安全的区间优化调度方法。在源荷预测误差波动区间的基础上，建立了计及频率安全的区间优化调度问题数学模型。为克服非线性频率安全约束导致的优化问题求解困难，通过近似化简将频率安全约束转换为线性约束。基于Benders分解方法，将区间优化问题原问题分解为基准场景下的主问题和不确定场景下校正调度的可行性校验子问题，根据违约程度筛选出高风险场景，减少了需考虑的场景数量。对修改后的10 机39 节点系统的仿真计算表明区间优化方法在确保调度方案安全性的同时有效地提高了计算效率。

需要指出，本文在对频率安全约束方程进行化简时，所采用方法具有一定的保守性，而且没有考虑风电的调频作用。如何减少模型的保守性，建立更为精细的模型，并针对大规模电力系统对算法进行考核是未来需要进一步研究的问题。

附录见本刊网络版（http：//www.epae.cn）。