基于实测数据跳变及稳态点的负荷模型参数快速辨识方法

孟 贤，沈一鸣，陈宇杰，曾丕江，吴 浩

（1. 云南电网有限责任公司电力科学研究院，云南昆明 650217；2. 浙江大学电气工程学院，浙江杭州 310027；3. 云南电网有限责任公司电力调度控制中心，云南昆明 650217）

0 引言

电力系统中各元件的精准建模是电力系统准确分析和控制的基础［1-7］。与其他元件相比，电力负荷具有复杂性和多样性的特点，并受季节、气候的影响［8］，其建模的不确定性较高，精度相对较低。随着电力系统规模的扩大和计算机技术的发展，电力系统仿真分析已经成为研究电力系统的主要方法，负荷模型的准确性对仿真分析结果有重要影响，不恰当的负荷模型会给电力系统仿真分析引入潜在的风险，危及系统的安全稳定运行。此外，随着现代电力系统的快速发展，分布式发电、储能装置以及电动汽车等新型电力元件大规模并网，这导致电力系统的负荷构成成分日益复杂，传统负荷模型典型参数在现代电网中的适配问题日益凸显，因此，近年来，学者对负荷建模和参数辨识问题开展了大量的研究工作。

负荷建模的目的是确定描述负荷特性的数学模型及其参数，使得实测功率和仿真功率之间的误差尽可能小。常用的经典负荷模型（CLM）和综合负荷模型（SLM）均采用电动机与静态负荷并联的结构，该结构在尽可能简化的基础上较好地反映了负荷静态和动态特性。在该模型结构下，模型参数对负荷模型的准确性有着至关重要的影响，因此，绝大部分负荷建模研究工作聚焦于模型参数的获取方法，主要方法有统计综合法［9-10］、故障拟合法［11］和总体测辨法［12-15］。

统计综合法的基本思路是根据负荷组成及占比、配电网参数以及负荷典型特性，通过统计综合，得出总体的负荷模型，该方法的物理模型清晰，便于定性刻画负荷特性，但存在统计工作量巨大、成分复杂等问题。故障拟合法本质上是一种试凑法，其基本思路是通过仿真实际系统故障，不断对负荷模型参数进行修正，直到仿真输出能够最好地拟合实际曲线。总体测辨法依靠实际电网故障量测数据，采用系统辨识技术对灵敏度较高的模型参数［16］进行估计，从而实现对测量点处负荷的准确建模，该方法不需要开展负荷调查，实施难度较小，因此，现有关于负荷建模的研究大多以该方法作为负荷建模方法。此外，近年来随着相量测量单元（PMU）／广域测量系统（WAMS）量测技术的快速发展以及电能质量监测装置及智能电表的广泛应用，电网扰动发生时的负荷数据已实现自动采集，这些累积的大量负荷量测数据也为总体测辨法的推广应用奠定了基础。

总体测辨法通常将负荷模型参数辨识问题转化为优化辨识问题，该方法首先通过暂态仿真计算负荷在给定参数下的各时刻功率值，然后利用最小二乘法、遗传算法、蚁群算法等多种优化方法优化负荷模型参数，缩小仿真功率和实测功率之间的误差。文献［14］提出一种基于改进粒子群优化PSO（Particle Swarm Optimization）算法的参数辨识方法，并通过实际数据验证该方法的有效性。文献［15］基于多组实际量测数据，采用遗传、单纯形混合算法对模型参数进行辨识，提高了负荷模型参数的适用性。

随着现代电力系统的快速发展，电力负荷多样性、复杂性和时变性的特点更加突出，这导致负荷参数具有复杂性和不确定性。负荷特性记录装置的任务是采集电压、电流互感器变换输出的模拟信号，将其转化为计算机可识别的数字信号并输入计算机辨识负荷模型参数［17］。由于数据通信以及存储问题，负荷特性记录装置所采集的数据通常就地离线保存在装置安装位置，但是负荷特性记录装置在电网中的分布过于分散，这使得数据收集工作给传统离线建模方法带来了巨大的挑战，因此，在负荷特性记录装置上增加负荷模型参数在线辨识功能的需求日益迫切。传统负荷模型参数辨识通常采用总体测辨法，由于在每次寻优时都要通过暂态仿真计算各时刻的功率值，计算量较大，计算时间较长，而由于成本问题，负荷特性记录装置通常采用性能不强的处理器（如ARM 9系列处理器），无法满足传统负荷模型参数辨识程序的计算需要［18］，因此，亟需发展基于负荷特性记录装置的在线总体测辨法快速负荷建模技术。

针对现有总体测辨法计算时间长、难以实现实时辨识的不足，本文提出一种基于实测数据跳变及稳态点的负荷模型参数辨识方法。该方法重点计算实测数据暂态突变等特殊点上的功率值，以特殊点上计算功率值与实际功率值误差最小为优化目标，避免了传统方法通过暂态仿真计算功率的过程，显著提高了计算速度。通过仿真和实际算例的比较研究，验证了所提方法的可行性和有效性。

1 基于总体测辨法的电力系统负荷模型参数辨识方法

1.1 经典负荷模型

电力系统分析中常采用经典负荷模型或者综合负荷模型，二者均由静态负荷和动态负荷并联组成，其结构清晰，物理含义明确，可以准确描述负荷静态和动态特性，是我国各电网实际使用的主流负荷模型［19］。本文采用经典负荷模型，其结构如附录A图A1 所示，图中静态负荷部分采用多项式模型，动态负荷部分采用三阶感应电动机模型。由于电力系统中频率波动通常很小，因此本文忽略频率对负荷模型的影响。

图A1 中，静态负荷模型通常表示为式（1）所示形式。

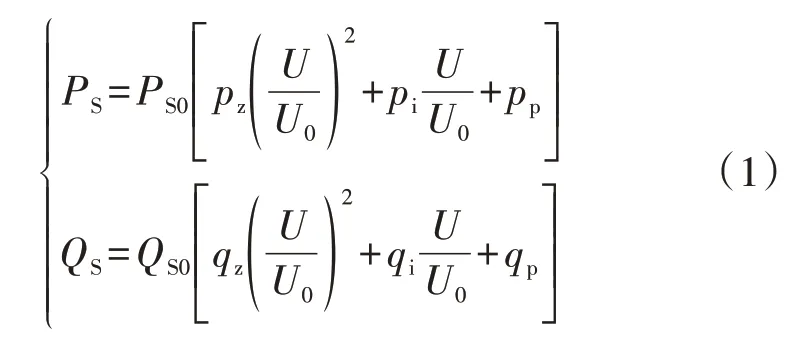
式中：PS、QS分别为静态负荷有功、无功功率；PS0、QS0分别为电压为U0时的静态负荷有功、无功功率，U0为稳态时负荷的额定电压；pz、pi、pp分别为有功功率恒阻抗负荷（Z）、恒电流负荷（I）、恒功率负荷（P）系数，表示3 种类型负荷消耗的有功功率占总静态有功功率的比例，满足pz+pi+pp=1，无功功率中的系数qz、qi、qp含义类似；U为静态负荷节点电压。

图A1中，动态负荷模型涉及感应电动机定转子电压方程和转子运动方程。

定子电压方程为：

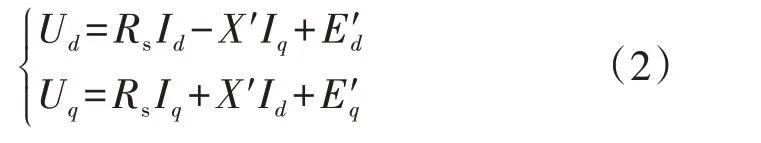
式中：Ud、Uq分别为负荷节点电压d、q轴分量；Rs为电动机定子回路中的电阻；Id、Iq分别为定子电流d、q轴分量；X′为电动机暂态电抗；E′d、E′q分别为暂态电势的d、q轴分量。

转子电压方程为：

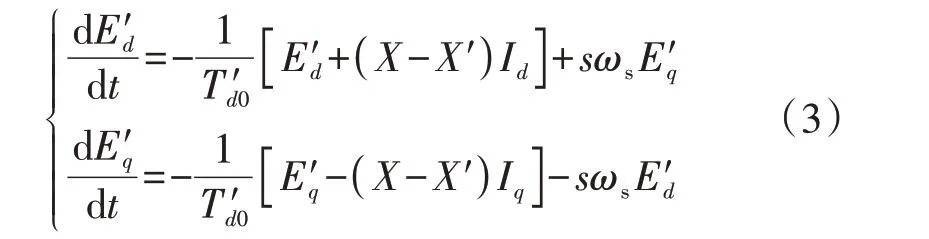
式中：T′d0为暂态开路时间常数；X为电动机开路电抗；s为电动机滑差；ωs为系统同步转速。

转子运动方程为：

式中：Tj为转子惯性时间常数；Tm、Te分别为电动机机械转矩、电磁转矩。

式（2）—（4）中参数可根据附录B 式（B1）计算得到。

感应电动机功率为：

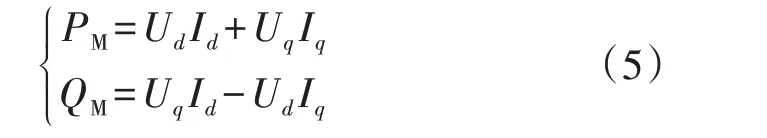
式中：PM、QM分别为电动机消耗的有功、无功功率。

除上述负荷模型参数外，为了确定电动机的基准功率，还需定义电动机初始有功功率占比Pper，表示初始稳态情况下电动机消耗的有功负荷占总负荷的比例。

负荷节点总功率由静态负荷和动态负荷消耗的功率组成，当电力系统发生扰动时，负荷节点电压变化，负荷节点总功率也随之变化，其值为：

式中：PL为负荷节点总有功功率；QL为负荷节点总无功功率。

1.2 总体测辨法

上述经典负荷模型中共有14 个独立的静态、动态负荷模型参数，同时辨识这14 个参数不仅实现困难，而且会降低参数辨识结果的准确性，因此，通常通过灵敏度分析挑选对功率响应灵敏度较高的部分参数作为重点辨识对象，而将其余参数固定为典型值［20］。据此，本文将负荷模型参数中灵敏度较大的电动机初始有功功率占比Pper、电动机定子回路中的电抗Xs、电动机初始滑差s0作为重点辨识参数。

采用传统总体测辨法进行参数辨识的主要步骤是寻找一组参数，使得通过式（7）计算得到的功率值与实测功率值之间的误差平方和J最小。

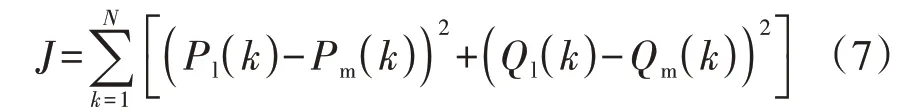
式中：N为采样点总数；Pm(k)、Pl(k)分别为第k点的实测、计算有功功率；Qm(k)、Ql(k)分别为第k点的实测、计算无功功率。

在进行优化辨识时，每次参数寻优后均需要通过暂态仿真计算各点上的功率值，并由式（7）得到功率误差平方和，再采用搜索、进化等方式获得更优的参数值。由于扰动量测数据的采样点较多，因此对所有采样点均进行功率计算时，需完整数值求解微分方程式（3），计算量较大，计算时间较长，考虑到重点辨识参数的数目不大，可通过直接计算少量特殊采样点的功率来辨识模型参数，从而缩短负荷模型参数辨识所需时间。

1.3 遗传粒子群混合优化算法

PSO 算法是一种模仿自然界中鸟群生物社会行为的优化算法，具有程序简洁易实现、并行搜索与计算效率高、寻优能力强、鲁棒性强的特点，广泛应用于电力系统复杂非线性问题的优化求解［21］。应用PSO 算法求解优化问题时，每组潜在解对应空间中的一个点，称之为粒子。适应性值的大小决定粒子位置的好坏程度，每个粒子会根据自身的当前位置、自身经历的最优位置以及群体的最优位置来调整飞行速度和方向，以此找到使适应性值最小的最优解。

当单纯采用PSO 算法求解负荷模型参数时，算法容易陷入局部最优解，无法得到全局最优解［21］。为了跳出局部最优解，提高种群的全局搜索能力，种群需保持一定的多样性水平，因此，在PSO算法的基础上，引入遗传算法GA（Genetic Algorithm）对其进行改进。GA源于达尔文的进化论思想，模拟生物在自然环境中的遗传和进化现象［21］，为了保持种群的多样性，GA 对较优个体进行交叉和变异操作，并按照“优胜劣汰”的原则将优秀的个体基因传至下一代，以此产生新的种群。

本文采用整体性能更优的遗传粒子群混合优化算法GP（Genetic Particle swarm hybrid optimization algorithm）求解负荷模型参数［22］，其基本思路为：首先根据PSO 算法进行第一阶段的优化，以提高算法的收敛速度；然后根据GA 进行第二阶段的优化，以保持种群多样性，防止算法陷入局部最优解［22］。

2 基于实测数据跳变及稳态点的负荷模型参数辨识方法

2.1 辨识思路

考虑到暂态跳变点、稳态时刻点在负荷模型参数辨识中的重要性，选取实测数据电压突降后1 点、电压恢复前后2 点以及最终稳态点共4 点计算负荷的有功和无功功率，并将这些点依次命名为第1—4点，同时选取电压突降前1 点作为初始稳态点，将其命名为第0 点。电压曲线跳变及稳态点示意图如图1 所示（图中电压为标幺值）。曲线中第1—3 点为实测数据跳变点，表现负荷的动态特性，第0、4 点为稳态点，用于辅助计算跳变点的状态变量E′d、E′q和s。

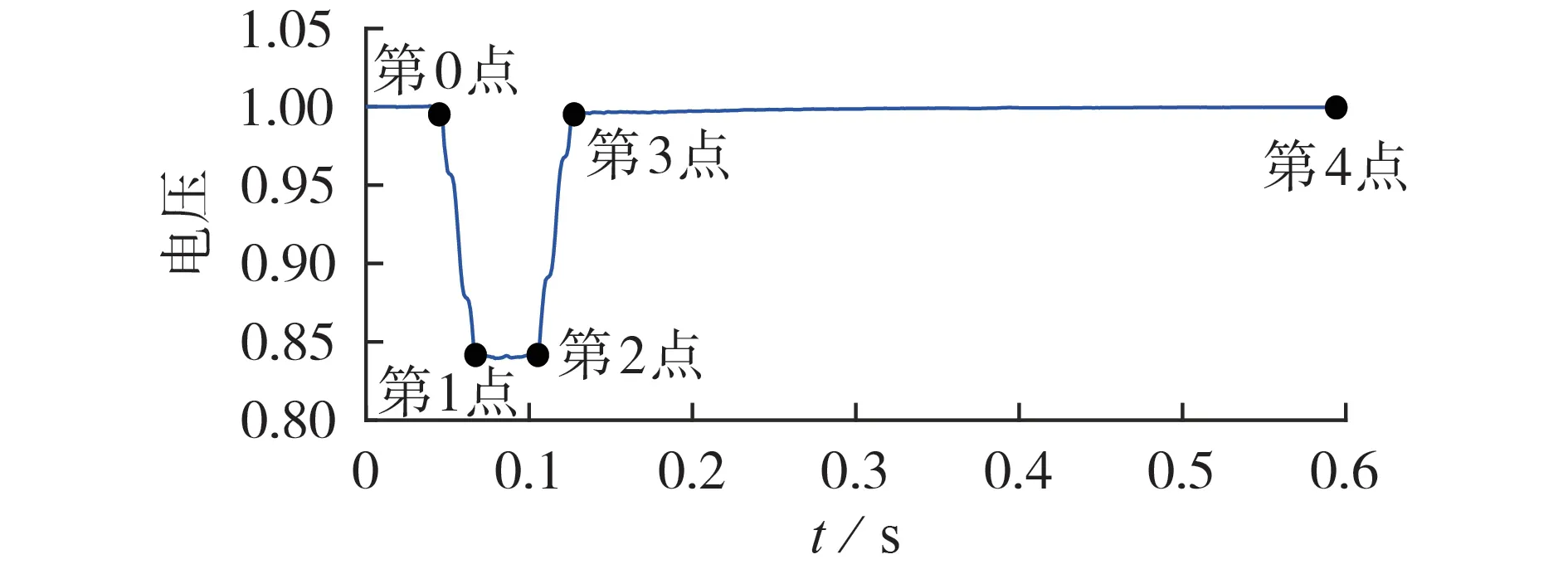
图1 电压曲线跳变及稳态点示意图Fig.1 Schematic diagram of jumping and steady-state points of voltage curve

由于经典负荷模型中含有复杂的微分方程，跳变及稳态点的有功和无功计算功率难以直接写为待辨识参数和量测电压的函数，因此，针对给定的待辨识参数，本文基于智能优化算法计算跳变及稳态点的有功和无功功率，进而以式（8）定义的功率误差平方和为优化目标，通过智能优化算法实现参数的寻优辨识。

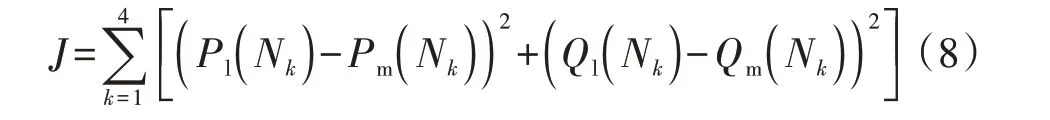
式中：Nk表示图1中的第k个点。

显然，当给定量测电压U( )k（k=1，2，3，4）以及待辨识参数时，跳变及稳态点上静态负荷的消耗功率可直接根据式（1）进行计算，但动态负荷的消耗功率与式（3）、（4）中的状态变量E′d、E′q和s有关，因此在计算式（8）前，需先确定4 个点的状态变量E′d、E′q和s。

2.2 跳变点及稳态点的选取方法

图1 中，第4 点为暂态过程结束后的稳态点，一般直接选取为录波数据的最后一点，第0—3点的求解问题可以转化为曲线变点检测问题进行求解。可以根据这4点将电压曲线分割为5段，以各段电压变化率与其平均值的偏差平方之和作为优化目标，数学函数如附录B式（B2）所示。通过优化方法求解式（B2）中的K1—K4，即为图1中的第0—3点。

2.3 第1、4点状态变量的计算

第1 点为电压突变点，由于电压突变的持续时间极短，因此可认为在此期间状态变量不会发生突变，即第1 点的状态变量值与第0 点的相同，而第0点的状态变量可由稳态初始化方法获得。

第4 点为最终稳态点，可利用稳态初始化方法计算其状态变量，即第4 点处的动态负荷状态变量不随时间变化，因此式（3）、（4）等号右边表达式的值为0，求解式（9）可得到第4点的状态变量。

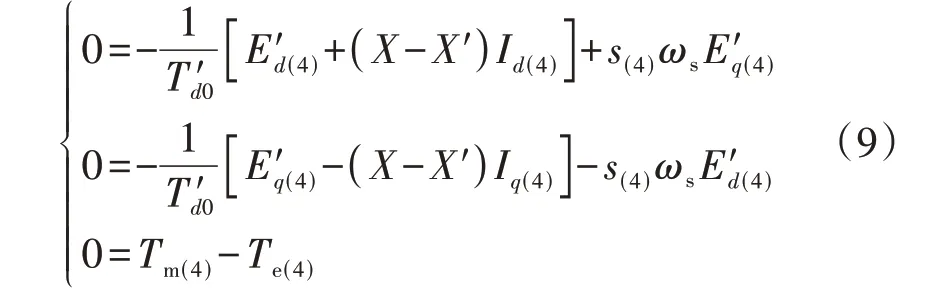
式中：下标“（4）”表示第4点。

2.4 第2、3点状态变量的计算

第2 点的状态变量需通过求解式（3）、（4）的非线性微分方程得到，由于难以直接求出式（3）、（4）的解析解，因此需采用数值计算方法。考虑到第1 点与第2 点间的扰动持续时间通常较长，这里采用大步长的隐式梯形积分方法［4］，即将式（3）、（4）的微分方程转换为式（10）所示的差分方程，式（10）中第1点的状态变量值已知，因此可迭代求解第2 点的状态变量值。

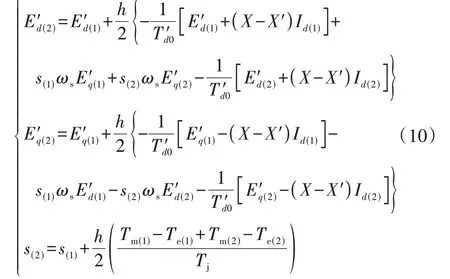
式中：h为第1 点和第2 点之间的时间间隔；下标“（1）”和下标“（2）”分别表示第1点和第2点。

第3 点为电压恢复后的第1 点，由于第2 点和第3点间的电压恢复持续时间极短，因此可认为第3点的状态变量未发生突变，从而第2点和第3点的状态变量相同。

2.5 所提负荷模型参数辨识方法的流程

通过2.2—2.4节所述方法可得到跳变及稳态点的状态变量值，再由式（1）、（2）、（5）、（6）得到各点上的有功、无功功率值Pl（k）、Ql（k），进而由式（8）求得跳变及稳态点的有功和无功功率误差平方和。在上述基础上，采用1.3 节的GP 进行负荷模型的参数辨识。考虑到PSO算法总惯性权重值对算法收敛速度和辨识精度的影响，这里采用变惯性权重的GP进行参数辨识［21］。

所提负荷模型参数辨识方法的流程图如附录A图A2所示，具体实施步骤如下：

1）输入实测电压、有功和无功功率值；

2）求解附录B 式（B2），得到实测数据的跳变及稳态点；

3）给定粒子种群数和迭代次数，并对所有粒子赋予初值；

4）按照2.2—2.4节所述方法计算跳变及稳态点上的状态变量值和对应的功率值，并由式（8）计算各粒子的优化目标函数J；

5）根据附录B 式（B3）更新粒子群的位置，对更新后较优的粒子进行交叉变异操作，并筛选得到下一代粒子群；

6）转至步骤4）继续进行优化计算，直至达到指定迭代次数。

3 算例分析

为了验证本文所提负荷参数辨识方法的有效性和可行性，分别使用仿真算例和实际算例进行分析。首先，构造已知负荷模型参数的仿真算例，对比辨识结果和实际仿真参数，以验证所提方法的可行性，并分析该方法在不同噪声水平下的鲁棒性；其次，基于某实际220 kV 变电站电能质量监测装置录波的实测扰动数据，对比所提方法和传统总体测辨法得到的辨识结果以及辨识所需的计算时间，以验证所提方法的有效性及实用性。各算例中粒子种群数为30，迭代次数为100，加速因子c1、c2均为1.5，交叉概率为0.7，遗传概率为0.3［21-22］。

3.1 辨识方法的可行性分析

对附录A 图A3 所示单机无穷大系统，使用BPA仿真软件进行故障仿真模拟，图中，负荷为感应电动机并联多项式模型的静态负荷，ZL为线路阻抗。设0 s时联络线长度的50%处发生三相短路故障，0.1 s时故障自动清除。仿真步长为0.001 s，记录故障前后负荷节点的电压、有功功率、无功功率数据，共记录1 s的数据。

文献［4，22］通过灵敏度分析指出，对于电动机自身的动态过程而言，灵敏度较高的参数为定子电抗、初始滑差、初始有功占比，其余参数可选取为典型值［4，20，23］，因此，本文对电动机初始有功功率占比Pper、电动机定子回路中的电抗Xs、电动机初始滑差s0这3 个参数进行辨识，并将其余参数固定为BPA 仿真计算时的典型参数，如附录C表C1所示［4］。

根据上述扰动仿真数据，采用本文方法辨识重点负荷参数。为了评价辨识结果的准确性，定义参数的辨识值与实际仿真值间的相对误差εY，如式（11）所示，定义辨识参数计算功率值与实际仿真功率值间的有功功率平均误差εPm和无功功率平均误差εQm，如式（12）所示。

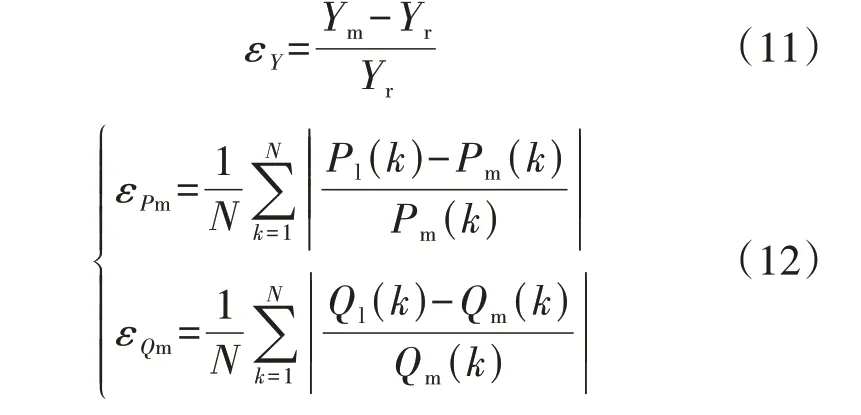
式中：Y表示Pper、Xs、s0；Ym为参数的辨识值；Yr为参数的实际仿真值。

由于优化算法的辨识结果具在一定的随机性，因此需对仿真数据进行多次辨识。附录C 表C2 为10 次辨识的结果及各参数的误差。由表可见：各次辨识结果间的差异较小，各参数辨识平均值与实际仿真值间的相对误差均在2%以下；各次参数的辨识值与实际仿真值间的相对误差较小，均不超过5%，这说明所提方法可行，且有较高的准确度；10次辨识结果的计算功率值与实际仿真功率值间的有功功率平均误差为0.87%，无功功率平均误差为0.74%，这表明功率曲线拟合度较高。图2 比较了10 次辨识结果平均值的计算功率曲线和实际仿真功率曲线（图中有功功率、无功功率均为标幺值）。由图可见，辨识结果平均值的计算功率曲线与实际仿真功率曲线基本一致，说明所提方法可行且辨识结果准确。

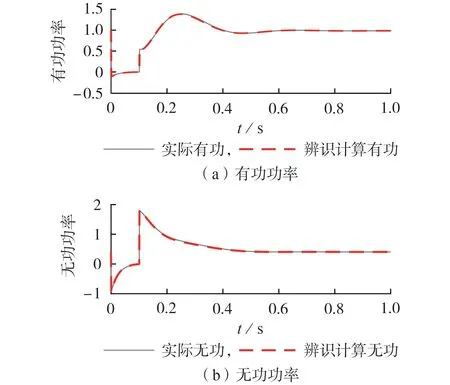
图2 三相短路故障下的辨识计算功率曲线和实际仿真功率曲线Fig.2 Calculative power curves by identification and actual simulative power curves under three-phase short circuit fault

3.2 辨识方法的鲁棒性分析

为验证本文方法的鲁棒性，对仿真数据叠加不同水平的白噪声（0、0.1%、…、5.0%），噪声服从高斯分布，分别计算辨识结果的有功及无功功率平均误差，如表1所示。

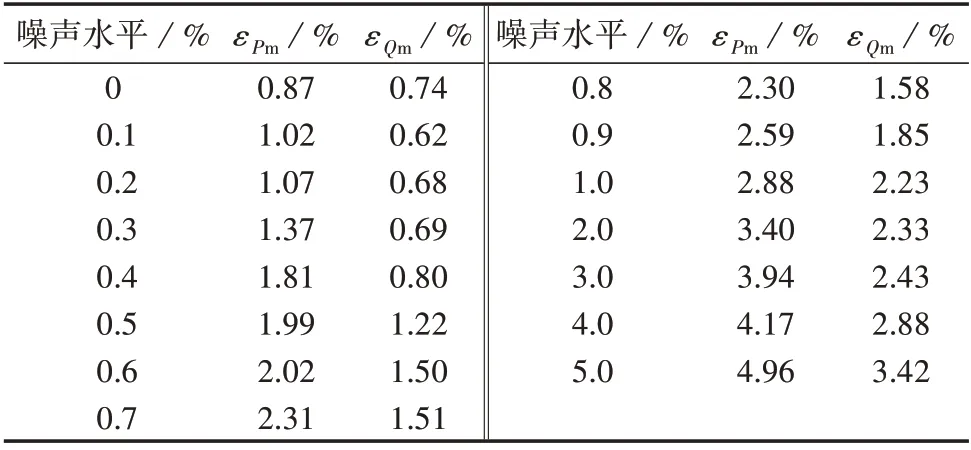
表1 不同噪声水平下的功率平均误差Table 1 Average power error under different noise levels

由表1 可知，当噪声水平低于1.0%时，本文方法的有功及无功功率平均误差均小于3%，即使噪声水平达到5.0%，功率平均误差也在5%以内，因此，本文方法具有较好的鲁棒性。负荷特性记录装置的精度为0.2 S，即测量误差在0.2%以内，因此本文方法在该精度下能够保证较高的准确率。

3.3 辨识方法的有效性分析

基于某实际电网中电能质量监测装置的录波数据，分别利用本文方法和传统总体测辨法进行参数辨识，其中重点辨识的3 个参数与3.1 节相同，其余11个固定参数取典型值，如附录C 表C1所示。录波数据的线路信息、故障发生时间及故障类型如附录C 表C3 所示。附录A 图A4 为线路1 在2017 年1 月9日（记为线路1a）及2017年4月7日（记为线路1b）的实际故障电压曲线及所提辨识方法选取的跳变及稳态点。

分别采用本文方法和传统总体测辨法对各线路进行10 次辨识，所得参数平均值以及相应的计算时长如附录C 表C4 所示。由于实际算例无法获取各参数真值，因此定义2 种辨识方法的参数相对偏差ε′Y、有功功率平均偏差ε′Pm和无功功率平均偏差ε′Qm，如附录B 式（B4）所示。各参数的偏差及2 种方法的平均计算时间如表2 所示（表中，t1、t2分别为本文方法和传统总体测辨法的平均计算时间）。由表可知：2 种方法得到的各参数辨识结果平均误差均在7%以内，参数取值均在合理范围内，比较符合实际情况；从计算时间来看，本文方法所需平均计算时间不到传统总体测辨法的1/10，因此，在保证辨识结果与传统总体测辨法基本一致的情况下，本文方法提高了辨识效率；对于对称及不对称故障，采用本文方法均能得到较好的结果，即使是故障时间短于1 个周期的数据（如附录A图A4中线路1a的电压曲线），采用本文方法也有较好的结果，说明本文方法具有较好的实用性。

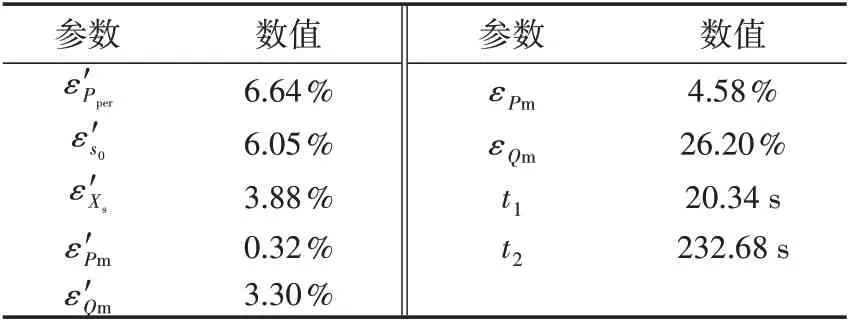
表2 实际系统负荷参数辨识结果Table 2 Load parameter identification results of actual system

附录A图A5和图A6分别对比了基于线路1a和线路1b的录波数据在2种方法辨识结果下的计算功率曲线和实际功率曲线。由图A5、图A6 及表2 可知：2 种方法的计算功率曲线基本一致，有功功率平均误差仅为0.32%，无功功率平均误差为3.30%；计算有功功率与实际有功功率较接近，两者间的平均误差仅为4.58%；计算无功功率与实际无功功率间的平均误差为26.20%，远高于计算有功功率与实际有功功率间的平均误差，其主要原因是部分线路无功功率较小，在故障时，无功功率出现了过零点，导致其平均误差偏大。

4 结论

本文提出一种基于实测数据跳变及稳态点的负荷模型参数辨识方法，针对实测数据电压突变后1点、电压恢复前后2 点以及最终稳态点，直接计算跳变及稳态点的有功和无功功率值，避免了传统方法所需的暂态仿真，减小了计算量，然后，以跳变及稳态点的计算功率值与实际功率值间的误差平方和最小为优化目标，采用GP进行负荷模型的参数辨识。

仿真算例表明，本文方法辨识结果准确，且具有较好的鲁棒性。实际算例表明，本文方法的计算时间不到传统总体测辨法的1/10，本文方法可应用于对称及不对称故障，具有较好的实用性。

附录见本刊网络版（http：//www.epae.cn）。