基于双延迟深度确定性策略梯度的船舶自主避碰方法*

刘 钊 周壮壮 张明阳 刘敬贤▲

（1.武汉理工大学航运学院 武汉 430063；2.武汉理工大学内河航运技术湖北省重点实验室 武汉 430063；3.武汉理工大学国家水运安全工程技术研究中心 武汉 430063；4.阿尔托大学工程学院机械工程系 芬兰艾斯堡 20110）

0 引 言

船舶作为水路运输的主体，是国家综合立体交通网的重要构成要素，其智能化已然成为了水运发展的必然趋势。《全球海洋技术趋势2030》《智能航运发展指导意见》《中国制造2025》《智能船舶发展行动计划（2019—2021）》和《交通强国建设纲要》等重要文件已明确指出：智能船舶是未来重要科技创新的新领域，人工智能、现代信息等高科技技术应用于航运业也是未来发展的必然趋势。自主避碰技术是船舶智能化发展面临的关键科学问题[1]，其研究受到各国学者的关注。

Lyu 等[2]通过将本船周围划分为4 个区域，并在每个区域设置不同的斥力势场函数，实现在多物标场景下及来船不协调行动时的安全避碰，但该方法航向变化波动较大，在部分场景下不满足大角度避让的要求。黄立文等[3]通过分析船舶会遇过程，结合船舶领域量化碰撞危险，并运用速度障碍法求解船舶在特定会遇态势下的动态避碰操纵区间，但是该方法假定1 次避让行动就能让清所有船舶，没有对整个避碰过程求解操纵区间。丁志国等[4]利用模糊理论评估船舶碰撞危险，结合《1972年国际海上避碰规则》（Convention on the International Regulations for Preventing Collisions at Sea 1972，COLREGs，以下简称《避碰规则》），对典型会遇场景进行仿真，实现在未知环境下2 船之间的安全避碰，但该方法未考虑多船避让问题。Wang等[5]提出了1种基于目标船舶意图推断的分布式避碰决策模型，该方法考虑了船舶操纵特性及《避碰规则》要求，但在一些极端情况下会出现对目标船意图的推断混乱情况，并造成避碰决策延迟。刘冬冬等[6]使用模糊理论方法结合四元船舶领域量化船舶碰撞危险，并应用粒子群优化算法以偏航距离、偏航时间为约束条件求解最短避碰路径，实现了2船之间的快速避碰，但该方法得到的避碰路径不符合船舶的操纵特性。Kim 等[7]使用遗传算法，通过避碰效果评价、是否到达终点，以及最小化航程等指标来对船舶转向角变量进行优化，得到了对于静态障碍物的有效避碰策略，然而该方法并不能做到实时避让且未考虑船舶之间的避碰问题。Zhang 等[8]提出了适用于多船会遇场景下的分布式避碰决策方法，该方法在特定场景下目标船操纵行动不协调或未按照《避碰规则》进行避碰操纵时依然具有较好的可靠性。朱凯歌等[9]引入Coldwell 船舶领域计算动态避让决策参数，并基于决策参数设计船舶避碰流程，实现了2 船之间的安全避碰；Kang 等[10]通过构建目标船的船舶领域来评估本船的碰撞危险，并结合差分进化算法设计受障碍物约束的适应度函数来寻找避碰最优路径，但路径的生成时间长，避碰效率低。

目前，深度学习在计算机视觉、语音识别、自然语言处理等诸多领域取得的突破性进展，极大地促进了人工智能的发展，深度神经网络极强的表征能力使得强化学习能够应用到更加复杂的决策问题上。目前已经有很多学者将深度Q 网络（Deep Q-learning network，DQN）[11]、深度确定性策略梯度（deep deterministic policy gradient，DDPG）、近端策略优化（proximal policy optimization，PPO）、SAC（soft actor-critic）等深度强化学习算法应用到船舶自主避碰中。Cheng 等[12]考虑外部环境干扰与船舶操纵性能，利用DQN算法实现对多个静态障碍物的转向与变速避让，但是该方法未考虑船舶之间的避碰操纵；王程博等[13]依据马尔可夫决策过程构建船舶避碰要素，利用深度强化学习算法进行训练，实现船舶与静态障碍物以及小角度交叉相遇局面下的安全避碰；周怡等[14]通过AIS 数据构建船舶的安全领域模型，并设计了基于避碰失败区域重点学习的DDPG 算法，实现了航道内2 船之间的避碰；Zhao等[15-16]依据《避碰规则》将本船周围划分为4 个区域来确定会遇局面，并结合船舶运动模型，利用PPO算法训练得到在2 船和多船场景下的避碰策略，但这些避碰策略都是针对特定场景训练得到的；Xie等[17]提出1 种基于异步优势演员-评论家算法和Q-learning算法的复合自适应避碰决策模型，该模型考虑了安全性与经济性，实现了多船避碰，但是该方法只针对1 种避碰场景进行训练，且避让过程认定目标船保向保速；周双林等[18]依据《避碰规则》划分让路船与直航船，并设计各自的奖惩函数，利用DQN 算法得到了不同会遇局面的避碰策略，但算法的训练是针对特定场景的，不具有普适性；Shen等[19]通过在目标船上添加规则线，使本船行动符合《避碰规则》的要求，并利用船舶领域构建适用于船舶避碰过程的强化学习模型，经过随机场景的训练得到了多船会遇场景下的避碰策略；Sawada 等[20]结合船舶领域构建目标障碍区并用来评估碰撞风险，利用连续动作空间下的PPO 算法在23 种多船会遇场景中进行训练，得到了基本符合《避碰规则》的避碰模型，同时通过对比实验得出了使用连续动作空间得到的避碰策略性能更高，但是该方法在避让过程中航向稳定性差，路径不平滑，避碰效果不佳；Chun 等[21]利用最小会遇距离（distance to closest point of approach，DCPA）、最小会遇时间（time to closest point of approach，TCPA）和船舶领域构建船舶碰撞危险度模型，结合PPO 算法对特定避碰场景进行训练并得到符合《避碰规则》的避碰策略，但是针对特定场景适用的模型很难推广到复杂的会遇局面中。

综上，已有研究中较好地解决了遵守《避碰规则》以及避让静态障碍物和单一目标船等问题，但在处理多船避碰时还存在避让实时性差、决策动作震荡严重、路径不平滑、普遍假设目标船保向保速等问题，特别是利用深度强化学习算法得到的避碰模型只针对特定会遇场景有效，模型泛化能力较弱[21-23]。针对上述不足以及船舶避碰决策信息的高维性和动作的连续性等特点，结合《避碰规则》与良好船艺，利用双延迟深度确定性策略梯度（twin delayed deep deterministic policy gradient，TD3）算法，提出1 种连续动作空间下的船舶自主实时避碰方法。该方法在随机场景下利用神经网络对船舶避碰算法进行迭代训练，提高模型的泛化能力，使其适用性更广。

1 基于强化学习的船舶自主避碰框架

为确保船舶在航行过程中能够安全有效的实时避让具有碰撞危险的目标船舶，提出基于TD3 的船舶自主避碰方法，其流程框架见图1。

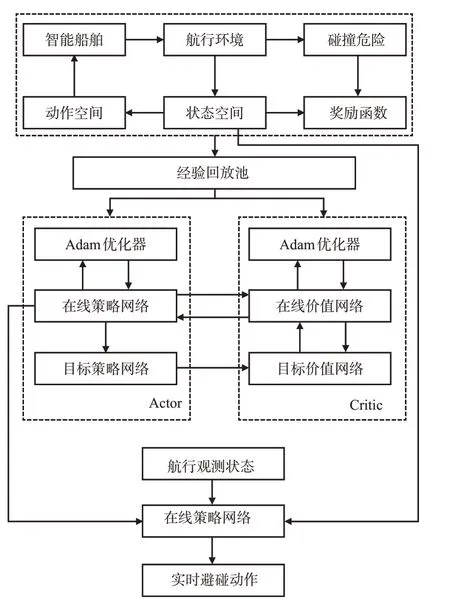
图1 船舶自主避碰框架Fig.1 Ship autonomous collision avoidance framework

首先，依据本船与目标船的实时航行信息，判断2船之间是否存在碰撞危险；其次，确定船舶自主避碰问题的强化学习要素，根据本船实时观测信息设计状态空间，依据船舶操纵特性设计动作空间，结合非稀疏化思想，考虑船舶与环境的交互情况设计符合《避碰规则》与良好船艺的奖励函数；然后，在船舶随机会遇场景下，结合强化学习要素，构成经验数组，利用Adam 优化算法更新深度神经网络参数，训练得到船舶自主避碰网络模型；最后，应用得到的避碰模型，实现2船会遇和多船会遇场景下的安全避碰。

2 面向避碰决策的强化学习要素设计

2.1 基于强化学习的船舶避碰原理

强化学习以马尔可夫决策过程（Markov decision process，MDP）作为基础理论框架，是解决复杂序贯优化决策问题的有效方法[24]。与其他机器学习算法相比，强化学习不需要事先给定标记过的训练数据，而是通过智能体（agent）与环境（environment）的不断交互试错来更新模型并习得策略。

船舶在航行中与环境发生交互得到连续避碰动作的过程可以视为序列决策过程，使用马尔可夫决策过程可以对其建模，使用强化学习算法能够对其求解。如图2 所示，船舶作为智能体是强化学习的学习者和决策者，环境代表与船舶相互作用的所有事物，在时刻t，船舶观测得到环境的状态st，依据此状态，船舶根据习得策略执行动作at，此时，船舶根据航行环境转移概率p进入下1 个状态st+1，并获得奖励rt+1。通过在环境中不断尝试采样，不断更新船舶避碰策略，使其获得最大累积奖励Gt（见式（1）），从而学习到最优避碰策略π*，见式（2）。

图2 强化学习基本原理图Fig.2 Reinforcement learning fundamentals diagram

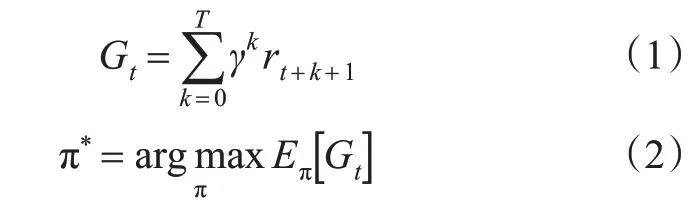
式中：γ∈[0,1]为1个用于确定短期奖励优先级的折扣因子，对于距离当前时间步越远的奖励，其重要性越低，通过减小γ的值，即可降低远期奖励影响当前决策程度；E表示期望。

由式（2）可见：最优避碰策略是指使累积奖励Gt的期望最大化的策略，累积奖励的期望一般以状态值函数Vπ(s)和动作值函数Qπ(s,a)表示。Vπ(s)是对未来奖励的预测，表示在状态s下，执行动作a会得到的未来奖励期望值，见式（3）；Qπ(s,a)主要用来评估船舶在当前状态s下选择动作a的好坏程度，见式（4）。

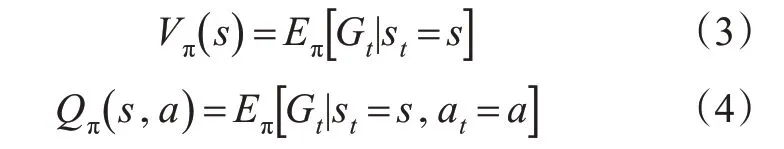
船舶避碰决策问题的强化学习基本要素主要为其在航行过程的状态，由1个状态转换到下1个状态对应的动作及执行动作后与环境交互所得到的奖励。

2.2 碰撞危险判断

判定船舶在航行过程中是否存在碰撞危险[2]，首先设定以dc为半径的碰撞危险监测范围圆，避碰模型会忽略监测范围以外的来船，然后设定船舶之间的安全距离ds，见图3。碰撞危险监测范围半径dc和安全距离ds可根据海况与会遇场景复杂程度进行适当调整，在宽阔水域，会遇场景简单等条件下更大，较大的dc与ds意味着船舶会尽早采取更大幅度的避碰行动。

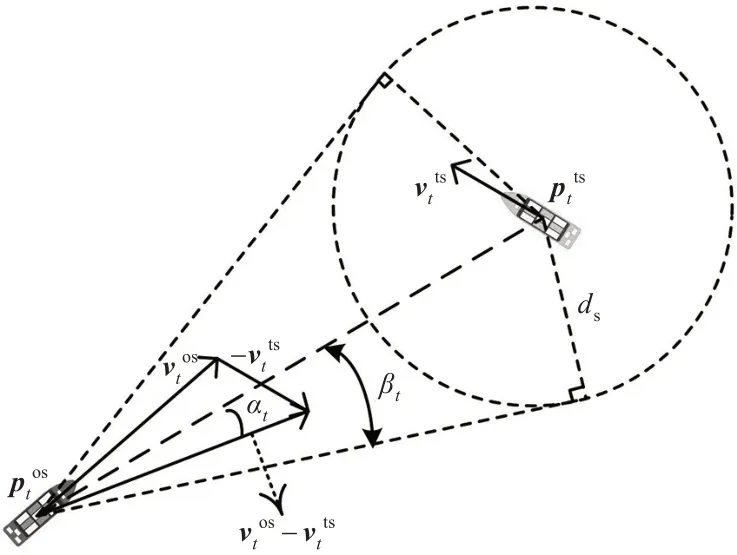
图3 碰撞危险判断示意图Fig.3 Collision risk judgment diagram

当来船进入监测范围时，依据本船与目标船的和速度延长线是否穿越半径为ds的圆来判断是否具有碰撞危险。如图3 所示，在t时刻，从本船位置坐标到半径为ds的船舶安全距离圆绘制2条切线，βt定义为任1 条切线与相对位置矢量（即）之间的角度，见式（5）。

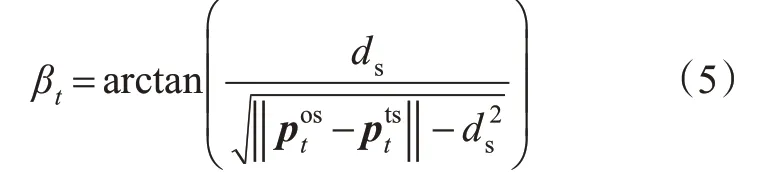
另外，当2船之间距离小于安全距离时，βt无法用式（5）计算。为此，在训练时，为了能让神经网络学到目标船不应进入本船的安全距离范围内这一策略，在训练过程中当本船与目标船的距离小于安全距离时认定为存在碰撞危险，设置βt=π。但是在船舶避碰实际应用中，当本船与目标船的距离小于安全距离且本船已经驶过DCPA点时，船舶间不存在碰撞危险，因此在避碰算法应用时设置βt=π/2。

图3 中αt是相对位置矢量与相对速度矢量（即）之间的夹角。当αt＜βt时，即表明与目标船存在碰撞危险，船舶应当采取避碰行动。具体来说，当船舶间距离大于安全距离时，若的延长线穿过半径为ds的圆则表明存在碰撞危险。当本船与目标船的距离小于安全距离ds时，在算法训练过程认为存在碰撞危险，并采取更大幅度的避碰行动。但在实际应用中，还需通过判断本船是否已经驶过DCPA点，即αt是否大于π 2 来确定是否存在碰撞危险，若大于π 2 则表明碰撞危险已经消失。

2.3 状态空间设计

式中：di为第i个区域内的目标船距离；hi为第i个区域内的目标船是否与本船存在碰撞危险。

式（6）所示的目标船状态信息指明了目标船的相对位置以及2 船是否存在碰撞危险。但是，为了使避碰模型做出合理决策还需要2船的相对航向和相对速度信息，因此，将连续4个时刻的目标船状态信息进行堆叠，构成自主避碰模型的可观测目标船信息状态空间，见式（7）。

另外目标船状态信息中的2船距离信息在输入到避碰算法时标准化到[-1,1]，标准化方式见式（9）。

对距离信息进行标准化，一方面能够使神经网络训练速度加快，另一方面方便在避碰算法实际应用时可以根据航行条件与会遇场景复杂程度随时调整碰撞危险监测范围圆半径dc与安全距离ds的大小。

2.4 动作空间设计

在船舶航行过程中遇到有碰撞危险的来船时，按照船员习惯做法通常采取改变航向的方式而不是改变航速大小以避免发生碰撞，并且频繁改变航速大小容易对主机造成损害。为保证船舶自主避碰算法给出的决策动作，具有良好的可操纵性，选择航向改变量作为动作空间，即at=Δψ。由于采用的TD3算法适用于连续动作空间，因此将本船避让操作所采取的航向改变量设计为：Δψ∈[-ψmax,ψmax] ，左转为负，右转为正，ψmax为单次决策可执行的最大转向角，不同船舶可根据自身操纵性进行设置。

避让船舶会依据可观测的状态信息做出避碰决策，当本船监测范围内存在具有碰撞危险的船舶时进行转向避让，直至驶过让清后继续朝目标点航行。

2.5 奖励函数设计

船舶自主避碰算法的收敛性依赖于合理的奖励函数设置，是船舶能够学习到安全有效的避碰策略的依据。结合非稀疏奖励思想设计奖励函数，使本船在无碰撞危险时朝向目标点航行，当本船与来船存在碰撞危险时采取符合《避碰规则》要求与良好船艺的避碰行动，进行安全有效的避让，直至驶过让清。

1）驶向目标点奖励。当本船碰撞危险监测范围内不存在需要避让的船舶时，首要任务是成功到达目标点。为应对稀疏奖励问题，采用基于势能的塑形奖励，以本船到达目标点为虹吸状态，当接近目标点时给予奖励，远离时给予惩罚，并且在到达目标点时给予1个较大的奖励，奖励函数见式（10）。

2）航向保持奖励。为了使本船在无碰撞危险时能够快速平滑的到达目标点，不发生偏航，以及存在碰撞危险时在避让完成后能够快速恢复航向，设计了航向保持奖励函数。当本船偏离航向时，对其进行惩罚，特别是目标点的相对方位角绝对值超过半个罗经点（π 32）时，持续得到值为rcourse的惩罚。航向保持奖励函数见式（11）。

3）碰撞危险奖励。当本船在航行中依据状态信息判定与来船存在碰撞危险时，本船应采取避让行动，保持与目标船的距离始终大于安全距离ds。为此设置为当目标船进入碰撞危险监测范围圆后，判断2 船之间是否存在碰撞危险，若存在碰撞危险给予惩罚，若本船与目标船发生碰撞，则获得1个较大的惩罚，奖励函数见式（12）。

4）规则量化奖励。当船舶间存在碰撞危险时，《避碰规则》明确要求了让路船与直航船应当采取的行动。由于本文主要研究开阔水域避碰过程中的让路行动，因此简要分析《避碰规则》第13～16 条中被要求采取行动船舶的避碰策略（见图4），船舶的当前航向用实线箭头表示，虚线箭头则表示让路船为避让来船可能采取的转向方向。在对遇局面下，构成碰撞危险的2 船各应向右转向，各从他船的左舷驶过；在交叉相遇局面下，《避碰规则》明确指出如果当时环境条件许可，让路船应避免横越他船的前方；在追越局面下，《避碰规则》没有明确让路船的具体行动，但是结合良好船艺的要求，当与被追越船航向会聚时，追越船应适当地改变航向，从被追越船的船艉驶过，当船舶间没有发生航向会聚时，可以根据本船的计划航线采取行动，如果被追越船在计划航线左侧时，追越船右转进行避让，反之则左转进行避让。

图4 船舶会遇避碰策略Fig.4 Collision avoidance strategy under the situation of ship encounter

通过分析3 种会遇局面下《避碰规则》的要求，结合驾驶员在避碰时的习惯做法，在开阔水域对遇和交叉局面下进行右转避让来避免形成紧迫局面是有效的，而在追越局面下追越船要依靠2 船的航向是否会聚来采取左转或右转的避让行动。考虑到设置奖励函数时难以对《避碰规则》详细量化，因此将右转避让策略作为神经网络的学习目标，此设置可以保证在开阔水域满足对遇、交叉相遇和右转追越的场景。在左转追越场景中，通过取目标船和目标点相对于本船方位角的相反数，输出避让动作的负值，实现船舶的左转避让。

因此，对构成碰撞危险的目标船进行右转避让时给予奖励，相反则给予惩罚，同时设置规则量化奖励值远小于碰撞危险奖励值，保证本船以安全避让来船为最终目的，奖励函数见式（13）。

式中：λrule为调整奖励大小的系数；ψmax为单次避让决策的最大转向角度；训练时设置λrule=2。

综上所述，为使船舶安全有效的避让目标船并到达目标点，设置了4 个奖励函数，其中Rgoal与Rcourse使本船快速平滑的向目标点航行，Rdanger和Rrule使本船周围存在其他船舶并有碰撞危险时能够快速有效的采取符合《避碰规则》的安全避让行动。由于该避碰模型适用于多船避碰，需要考虑在碰撞危险监测范围内避让多个目标船获得的奖励，因此总的奖励函数设置见式（14）。

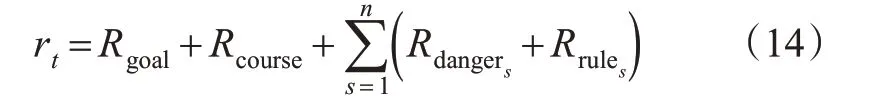
式中：n为处于本船碰撞危险监测范围内的目标船数量；Rdangers为第s艘目标船产生的碰撞危险奖励；Rrules为第s艘目标船产生的规则量化奖励。

3 基于TD3算法的船舶避碰决策

基于策略的深度强化学习算法可以分为随机性策略和确定性策略。随机性策略通过概率分布来表示，即在状态st下以一定的概率选择动作at；而确定性策略根据状态st直接选择动作at，这是1 个确定性过程，即中间没有出现概率，不需要进行选择。因此，确定性策略深度强化学习算法相比于随机性策略，可以在低采样数据下提高计算效率。

TD3算法是1种无模型（model-free）确定性策略的深度强化学习算法，适用于具有连续动作空间的决策任务。TD3主要针对DDPG算法对Q值的过高估计等问题进行改进，使其训练更稳定，性能更强。目前，TD3 已经成为支持高维空间连续型控制任务的高性能算法，相比DQN、DDPG、PPO、SAC等算法拥有更好的决策效果[25-26]。

因此，为了保障船舶避碰决策的高效性，针对船舶避碰决策状态空间的高维性和动作的连续性等特点，选取TD3 算法构建基于深度强化学习的船舶避碰决策模型。

3.1 算法网络结构设计

TD3 算法使用了Actor-Critic 结构，因此避碰模型中包括策略网络与价值网络，策略网络依据状态信息输出避碰动作，价值网络输出Q值来评判动作的好坏程度，算法同时为策略网络和价值网络分别搭建了各自的目标网络，克服训练的不稳定性。

结合船舶自主避碰模型的状态空间st=[]。其中：为连续4个时刻观测到的目标船信息，设计了含有4个隐藏层的策略网络，网络结构见图5。使用前2 层LSTM 网络处理连续4 个时刻的目标船信息，其中第1 层为一维卷积LSTM 网络，卷积运算包含128 个通道，卷积核大小为2，步长为1；第2 层LSTM网络包含128个神经元；经过LSTM网络处理后与目标点信息合并输入到2 层的全连接网络，每个全连接层包含256 个神经元，并采用ReLU非线性激活函数。输出层是包含1个神经元的全连接层，使用双曲正切函数作为激活函数，将输出标准化到[-1,1]之间，与ψmax相乘后输出动作at。价值网络采用类似的网络结构，与策略网络的主要区别在于第1个全连接层的输入要增加当前时刻的动作at，并且输出层不使用任何激活函数，直接得到Q值。价值网络和策略网络均采用Adam优化算法训练。

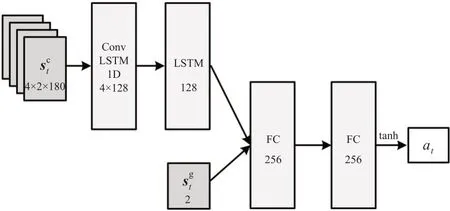
图5 船舶自主避碰策略网络结构Fig.5 Actor network structure of ship autonomous collision avoidance

3.2 算法网络更新

为了缓解价值网络对Q值的过高估计，TD3 算法同时训练2 个完全相同的价值网络，每次计算目标Q值时总是选择其中较小的值，降低高估误差。同时，为了降低目标Q值计算的方差，并缓解确定性策略对动作值函数局部“窄峰”的过拟合倾向，在船舶观测状态sj+1下目标策略输出的基础上添加1个随机高斯噪声ῆ，这种方式被称为目标策略平滑。综上，目标Q值与价值网络的损失函数见式（15）～（16），其中损失函数使用了平滑平均绝对（huber）误差，见式（17）。

式中：yj为第j个训练样本的目标Q值；lQ为价值网络的损失函数；rj第j个训练样本当前时刻的奖励值；sj为第j个训练样本当前时刻的状态信息；sj+1为第j个训练样本下1个时刻的状态信息；aj为第j个训练样本当前时刻船舶采取的避碰动作；c为策略平滑噪声的截断边界值；θi为第i个价值网络的参数；θ′i与ϕ′分别为第i个目标价值网络参数和目标策略网络参数。

此外，为了减少目标值计算的方差对策略学习的负面影响，算法降低了策略网络参数ϕ与目标网络参数ϕ′和θ′i的更新频率，以保证价值网络经过充分学习降低方差之后再影响策略网络和目标网络，即每更新m次价值网络再更新1 次策略网络，梯度∇ϕJ默认来自价值网络中的Qθ1，见式（18），并采用软更新方式更新目标网络，见式（19）。

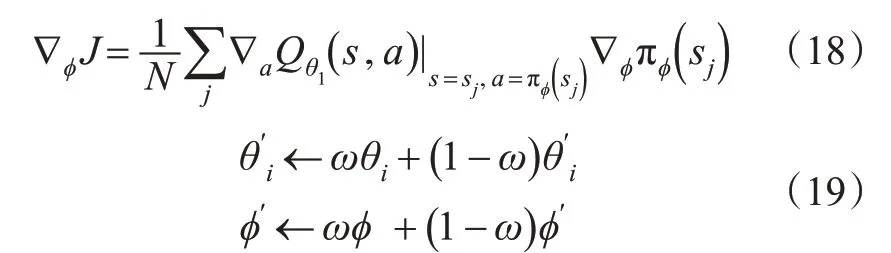
式中：ω为系数，用来控制目标网络参数的更新速度。

3.3 算法流程

船舶自主避碰策略的学习过程是TD3算法中深度神经网络的收敛过程，其中神经网络的输入为本船在航行过程中观测到的实时状态信息，策略网络依据价值网络对策略好坏的评判来更新网络参数，价值网络通过最小化误差损失函数来更新网络参数。另外TD3 算法使用了经验回放技术去除样本间的相关性和依赖性，同时通过随机场景对模型进行训练以增强泛化能力，船舶自主避碰算法流程见图6。

图6 船舶自主避碰算法训练流程Fig.6 Training process of ship autonomous collision avoidance algorithm

4 船舶自主避碰算法训练与对比仿真验证

为了验证避碰算法的效果，首先介绍船舶避碰训练环境搭建与模型参数设置；然后将训练好的船舶避碰模型应用于常见的2 船会遇场景中，分析船舶的避碰效果；最后船舶在多船会遇场景下进行避碰实验，展现模型的良好性能。

4.1 实验设置

基于深度强化学习环境OpenAI Gym，在Windows 10 平台上搭建船舶自主避碰决策仿真实验环境，硬件环境和软件环境具体信息见表1。

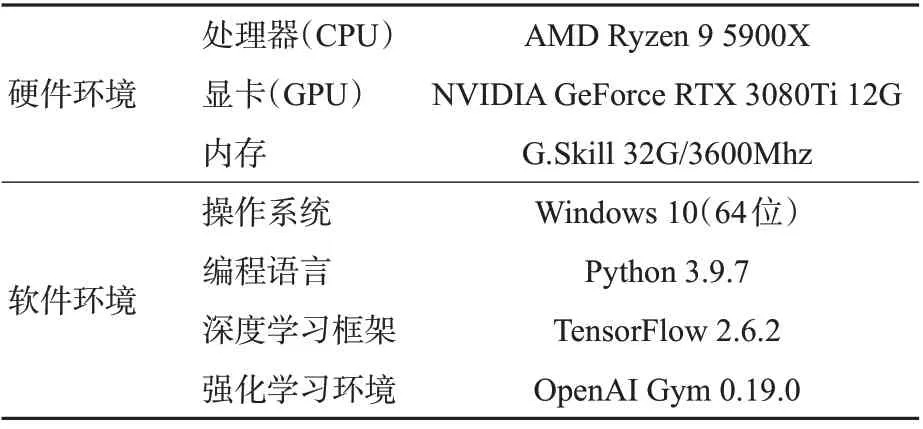
表1 实验环境信息Tab.1 Experimental environment conditions

针对船舶自主避碰的强化学习任务，设计了1个12 n mile×12 n mile的正方形作为航行训练区域，设置本船起点（0，0），目标点（10，10），航速12 n mile/h，dc=4 n mile，ds=4/3 n mile，本船膨化圆半径τ=0.25 n mile，依据船舶操纵特性，设置最大转向角ψmax=5°，决策时间间隔为15 s[2]。为了让训练得到的船舶避碰算法普遍适用于各种会遇场景，在训练区域中随机生成x艘船舶（x∈[1,7]），并且目标船的位置、航向和航速均随机设置，模拟船舶遇到各种会遇场景，并对避碰失败场景着重训练。当本船到达目标点或者发生碰撞则对场景重置并开始下1回合训练。

为了降低模型的训练难度，实验中采用跳帧（frame skipping）操作，即相邻2 次决策之间的f帧都重复上1 次的动作，综合权衡避碰性能与训练难度，确定f=2。同时，为了在训练时提高模型的探索能力，采用输出动作加入高斯噪声η～N(0,σ)的方法来实现，并在正式训练之前让本船在环境中进行随机探索。为了使避碰算法能够快速平稳的收敛，在训练时设置批量采样大小和更新次数随着迭代次数增加而增大。TD3算法的相关训练参数设置见表2。

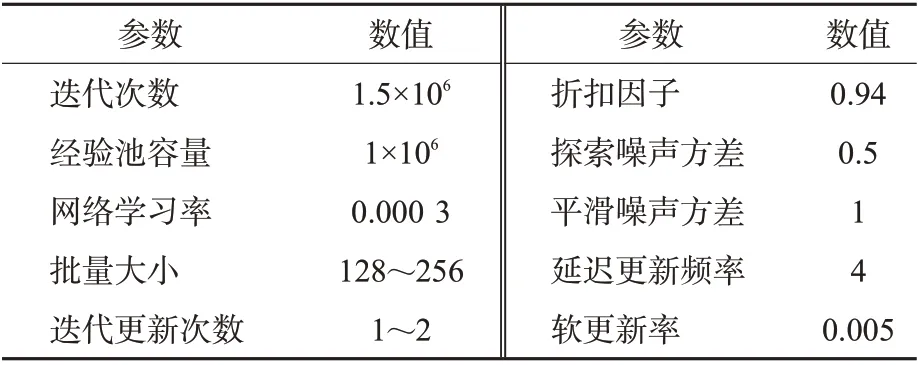
表2 船舶避碰算法训练参数Tab.2 Training parameters of ship collision avoidance algorithm

基于上述实验环境对船舶自主避碰算法进行了150 万次迭代训练，结果见图7，累积奖励随着算法不断迭代训练慢慢增大，在迭代122 万次后趋于平稳，此时累积奖励值大小在91.867上下波动，波动范围在[-16.293,18.169]之间，收敛效果较好。

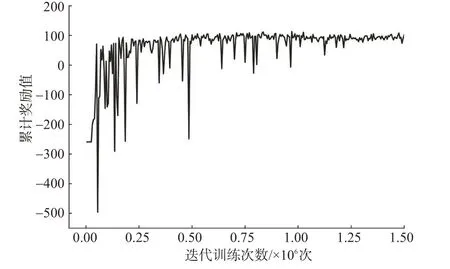
图7 累积奖励变化曲线Fig.7 Total reward curve

4.2 2船避让对比仿真验证

为验证提出的船舶自主避碰算法能按照《避碰规则》要求和良好船艺在2 船会遇局面下安全有效的避让目标船，分别对《避碰规则》中定义的3 种会遇局面进行仿真验证，并与改进人工势场[2]（artificial potential field，APF）避碰算法进行比较，均设置本船（own ship，OS）起点坐标（0，0），目标点（goal）坐标（10，10），船速12 n mile/h，航向45°，每次最大转向角度ψmax=5°，船舶间安全距离ds=2 n mile。特别的，改进APF 算法中的参数设置为Ros=0.5 n mile，Rts=0.5 n mile，dsafe=1 n mile，这样设置可以保证2种避碰算法的安全距离都为2 n mile，其他参数均采用文献[2]的原始设置。

1）追越局面。追越局面下设置目标船（target ship，TS）起始位置（3.2，3.4），航速5 n mile/h，航向45°，在2种避碰算法中，均设置本船的碰撞危险监测范围半径dc=4 n mile。由2船相对位置可知，目标船位于本船船首方向，且在本船与目标点连线的左侧，舷角-1.736°，2船航向不发生会聚，结合《避碰规则》要求与良好船艺，本船进行右转避让。2种避碰算法仿真实验的船舶航行轨迹见图8，本船避碰过程中航向变化量见图9，图10绘制了2船距离随时间的变化曲线。

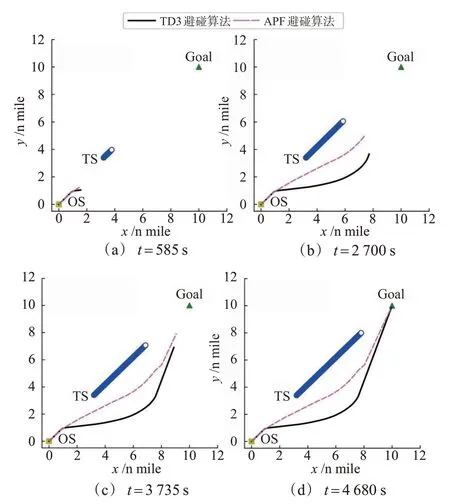
图8 追越局面船舶轨迹图Fig.8 Ship trajectory diagram of overtaking situation

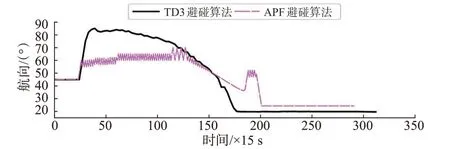
图9 追越局面本船航向变化曲线Fig.9 Course change curve of own ship in overtaking situation

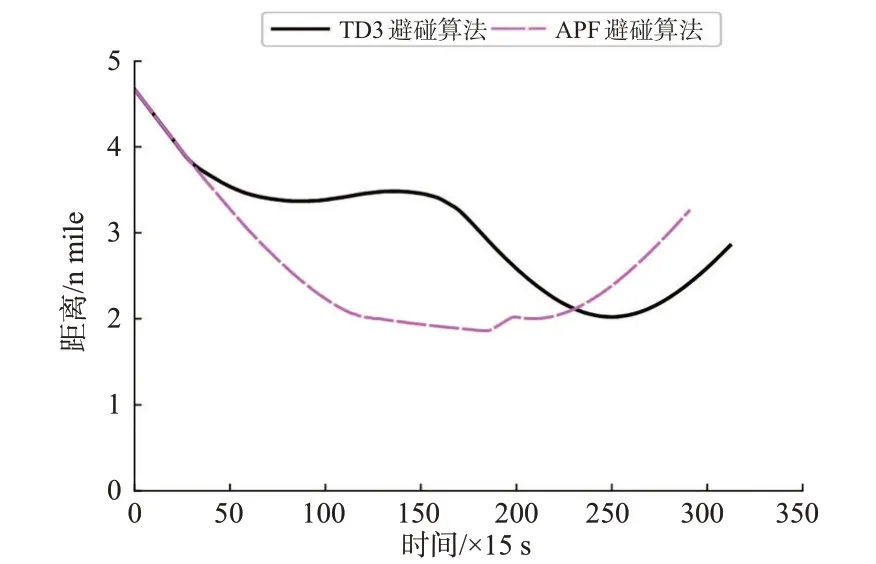
图10 追越局面船舶间距离变化曲线Fig.10 Curve of distance between ships in overtaking situation

由追越局面仿真结果可知，在t=360 s，距离目标船3.969 n mile时，本船监测到与来船存在碰撞危险，并按照《避碰规则》要求和船员良好船艺迅速右转40°避让来船；随后为避免过快恢复航向而与目标船再次构成碰撞危险，本船开始缓慢向左转向，并在t=2 700 s，航向恢复到朝向目标点；在t=3 735 s，2 船之间的距离达到最小值2.022 n mile，此时本船已经从目标船的艉部驶过；在t=4 680 s本船达到目标点。

在改进APF 避碰算法中，本船在t=345 s 发现目标船，并迅速右转15°，之后本船航向在56°～61°之间震荡，从t=795 s开始本船航向在57°～62°之间震荡，在120 s之后，航向又在60°～65°之间震荡；在t=1 935 s，本船开始恢复航向；在t=2 760 s，本船与目标船达到最近距离1.861 n mile，目标船进入船舶安全距离圆内，因此本船迅速右转16°使目标船驶出安全距离范围，最后恢复航向并到达目标点。

同时，为了验证训练得到的避碰模型对于左转场景下的适用性，设置目标船起始位置（3.6，3.2），航速4 n mile/h，航向45°，本船dc=4 n mile。此时目标船位于本船船首方向，舷角3.366°，在本船与目标点连线的右侧，2 船航向未发生会聚。图11 分别为追越局面左转场景下2 种避碰算法的船舶轨迹图、船舶间距离随时间变化图和本船航向变化图。

图11 追越局面左转场景仿真结果Fig.11 Simulation results of left turn scenario in overtaking situation

在船舶避碰过程中，由于改进APF 避碰算法的输入并不是全局状态信息，只在与目标船构成碰撞危险时才会输入来船的状态信息并形成斥力，因此本船的航向改变量小且震荡严重，而且由于目标点引力与目标船斥力的动态变化，导致在引力大于斥力时容易使目标船进入本船的安全距离范围。与改进APF 算法相比，基于TD3 的船舶避碰算法在追越局面下航向改变幅度大，变化快速平稳，震荡较小，避碰路径更加平滑，并且在避让过程中2 船之间的距离始终大于安全距离2 n mile。

2）对遇局面。对遇局面下设置目标船（TS）初始位置（8.5，8.5），航速10 n mile/h，航向225°，2种避碰算法的本船dc=6 n mile。依据《避碰规则》，构成对遇局面的2 船应各自右转从对方船的左舷驶过，为了达到共同行动的目的，目标船也使用本文提出的基于TD3的避碰算法。2种避碰算法的仿真结果见图12～15：图12 为船舶不同时刻的航行轨迹图，图13为本船的航向变化信息，图14为目标船的航向变化信息，图15为2船间距离随时间的变化曲线。

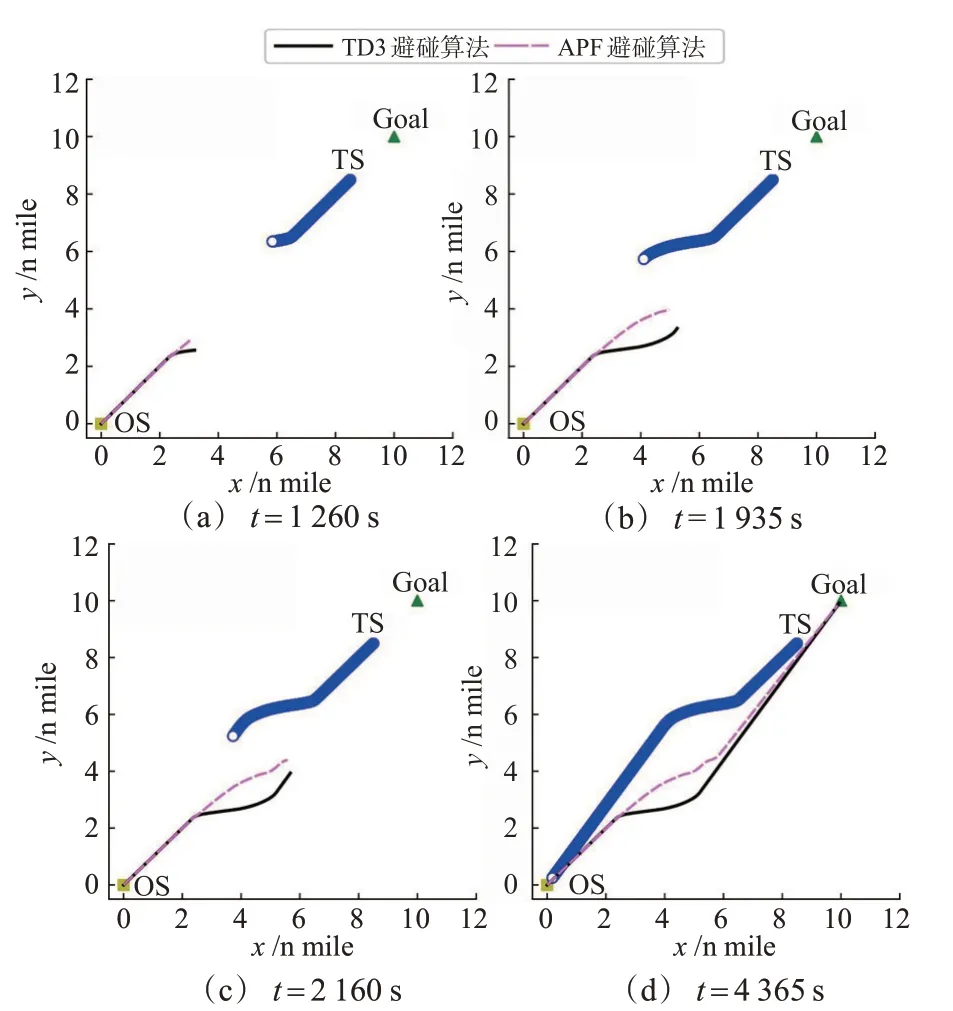
图12 对遇局面船舶轨迹图Fig.12 Ship trajectory diagram of head-on situation

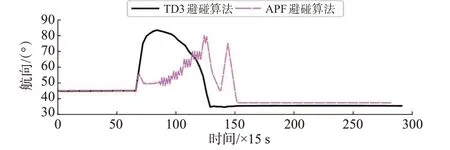
图13 对遇局面本船航向变化曲线Fig.13 Course change curve of own ship in head-on situation

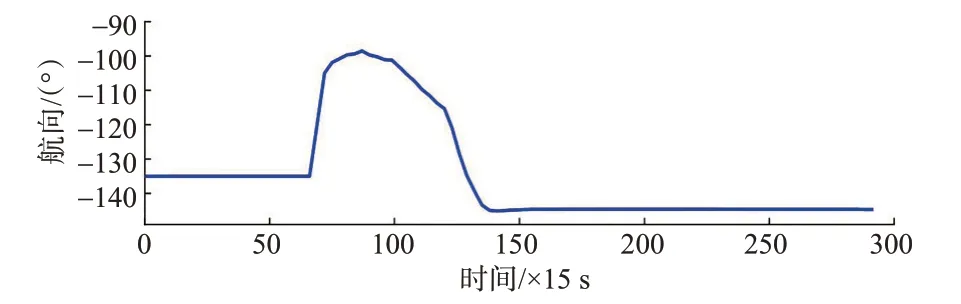
图14 对遇局面目标船航向变化曲线Fig.14 Course change curve of target ship in head-on situation

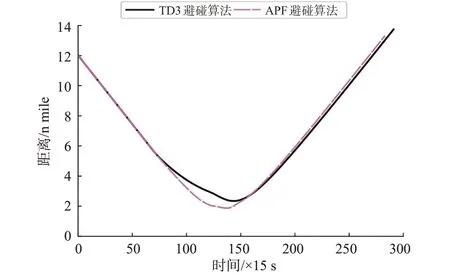
图15 对遇局面船舶间距离变化曲线Fig.15 Curve of distance between ships in head-on situation

由仿真结果可知，在t=990 s，本船与目标船之间的距离达到5.971 n mile，形成对遇局面，依据本文提出的避碰算法，本船迅速右转38.5°以避让来船，此时目标船也向右转向37°进行避让；随后，本船开始缓慢恢复航向，并在t= 1 395 s航向恢复至朝向目标点，135 s之后目标船航向恢复；在t= 2 160 s本船与目标船左舷对左舷以最小距离2.345 n mile 安全通过；在t= 4 365 s 本船到达目标点，整个避让过程中本船采取的行动安全有效，2船之间距离始终大于2 n mile。

由改进APF 避碰算法的船舶避碰仿真结果可知，本船在t=990 s发现来船并右转10.8°，之后本船航向又减少至49°附近；从t=1 275 s开始，本船航向边震荡边增大，并在585 s后达到最大值80°，随后航向开始恢复；在t=2 055 s，本船与目标船的距离达到最小值1.871 n mile，105 s 后本船航向突然增加30°，产生1个较大的波动，波动过后本船朝向目标点航行，并于t=4 245 s到达目标点。

由对比结果可知，改进APF 避碰算法在对遇局面下比本文算法提前到达目标点，但是船舶间不能满足设定的安全距离，且航向变化幅度小，由于在判定目标船无危险后斥力消失而导致本船过快恢复航向又构成危险的情况，使本船航向震荡较多。相反，本文提出的避碰算法在对遇局面下航向变化幅度大且平稳，并满足安全距离要求。

3）交叉相遇局面。交叉相遇局面下设置目标船（TS）初始位置（9，0），航速12 n mile/h，航向315°，本船dc=6 n mile。2种避碰算法仿真的船舶航行轨迹见图16，图17为本船航向随时间的变化曲线，2船距离的变化曲线见图18。

图16 交叉相遇局面船舶轨迹图Fig.16 Ship trajectory diagram of crossing situation

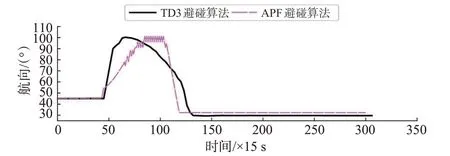
图17 交叉相遇局面本船航向变化曲线Fig.17 Course change curve of own ship in crossing situation

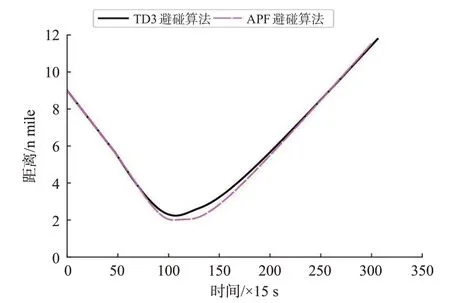
图18 交叉相遇局面船舶间距离变化曲线Fig.18 Curve of distance between ships in crossing situation

由TD3 避碰算法的仿真结果可知，本船在t=720 s 发现与来船形成交叉相遇局面，2 船相距5.817 n mile，本船作为让路船在《避碰规则》的约束下迅速向右转向55°，在t=990 s，本船开始缓慢恢复航向，于t= 1 620 s，2 船间距离达到最小值2.237 n mile；在t=1 980 s，本船航向恢复到朝向目标点，之后本船从目标船的艉部驶过，实现对来船的安全避让；在t=4 590 s，本船到达目标点，整个避让过程2船间的距离始终大于安全距离2 n mile。

由改进APF 避碰算法的仿真结果可知，本船在t=645 s发现来船，此时2船相距5.959 n mile，30 s后本船以相对较慢的速度向右转向58°，转向过程中震荡严重；在t= 1 560 s，2 船之间距离达到最小值1.999 n mile，随后本船开始恢复航向；在t=4 500 s，本船到达目标点。

在交叉相遇局面下，改进APF 避碰算法比追越和对遇局面效果好，能够大幅度的避让来船，但是航向变化速度相比本文算法慢，且震荡情况依然存在。本文避碰算法避让行动迅速、改向幅度大，路径相对更加平滑。

综上，通过在船舶追越、对遇和交叉相遇局面下的避碰仿真实验结果可以得出，提出的避碰算法能够使本船在与目标船舶构成碰撞危险时做出安全有效的避碰决策。由于本文避碰算法的输入为全局的状态信息，即使与目标船不存在碰撞危险时也会关注来船的实时动态，因此相比于改进APF算法，本文算法的航向变化快速平稳，转向幅度大，避碰路径更加平滑，并且与目标船的距离始终大于安全距离。

4.3 多船避让对比仿真验证

在船舶实际航行过程中，会遇到与多艘船舶构成碰撞危险的局面，相比2船避让，多船避让局面更为复杂。为验证提出的避碰算法在复杂会遇场景下仍具有良好性能，与改进APF 避碰算法进一步进行多船避让仿真对比实验。

1）多船避让仿真实验。在避让多船的仿真实验中，本船的初始航行参数不变。在本文算法中设置本船碰撞危险监测圆半径dc=4 n mile，安全距离ds=4/3 n mile。在改进APF 避碰算法中依据文献[2]，将本船的碰撞危险检测距离设置为6 n mile，Ros=0.5 n mile，Rts=1/3 n mile，dsafe=0.5 n mile，这样设置可以保证2 种避碰算法的安全距离都为4 3 n mile，其他设置均来自文献[2]，另外2 种算法中本船每次转向的最大幅度均设置为5°。目标船的初始设置见表3，为了验证2 种算法的可靠性，将引入目标船的不协调行动，具体为：在t=1 035 s，目标船左转30°干扰本船的行动。

表3 多船会遇场景目标船初始设置Tab.3 Initial setting of target ship in multi-ship encounter scenario

多船会遇仿真实验中船舶航行轨迹见图19，图20 为航行过程中本船航向的变化曲线，2 种算法下本船与目标船距离随时间的变化曲线见图21～22。

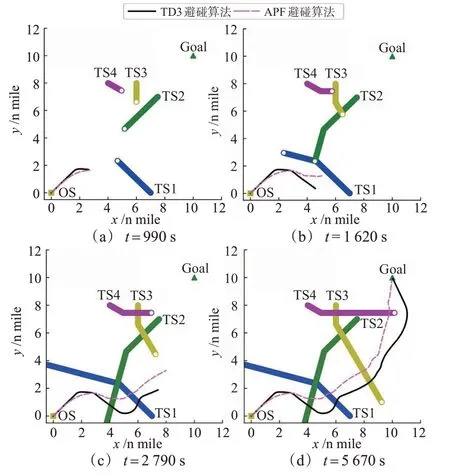
图19 多船会遇场景船舶轨迹图Fig.19 Ship trajectory diagram of multi-ships encounter scenario

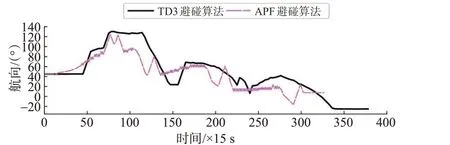
图20 多船会遇场景本船航向变化曲线Fig.20 Course change curve of own ship in multi-ships encounter scenario

图21 TD3避碰算法下本船与目标船距离变化曲线Fig.21 Curve of distance between own ship and target ships under TD3 collision avoidance algorithm

在图19（a）中，最初本船朝向目标点航行，在t=675 s，本船发现与目标船1相距3.816 n mile，形成交叉相遇局面，本船依据《避碰规则》迅速向右转向51°，避免横越目标船1 的前方；在t=990 s，本船发现目标船2 且相距3.925 n mile，经过计算，2 船之间无碰撞危险，本船未做出反应。

图19（b）中，在t=1 035 s，目标船1 与目标船2突然左转30°，这导致本船与2艘目标船之间重新构成碰撞危险，本船迅速右转33°同时避让2船；在t=1 215 s，本船与目标船1达到最近距离1.355 n mile，驶过让清目标船1。

图19（c）中，从t=1 755 s开始，本船逐渐恢复航向；在t = 2 015 s，本船与目标船2 达到最近距离1.637 n mile，驶过让清目标船2，180 s后本船航向恢复至朝向目标点；在t=2 340 s本船发现目标船3，距离达到3.906 n mile，由于目标船3 未按照《避碰规则》进行右转避让，本船迅速右转44°以避免紧迫局面。

在图19（d）中，本船与目标船舶3 在t=3 420 s达到最小距离1.376 mile；180 s 后，目标船4 与本船距离达到3.953 n mile 且未进行避让，本船右转35°以避免紧迫局面发生；随后本船开始恢复航向，并在t=5 670 s到达目标点。

由改进APF 避碰算法的仿真结果可知，本船在与目标船1 相距5.939 n mile 时，开始缓慢右转进行避让，并在t=645 s航向发生震荡，此时本船与目标船2的距离达到5.973 n mile，但并不存在碰撞危险；在t=1 035 s，由于目标船1 和目标船2 的不协调行动，本船继续右转40°避让2船，随后开始恢复航向，并在t= 1 245 s 与目标船1 达到最小距离1.209 n mile，570 s后与目标船2达到最小距离1.045 n mile；在航向恢复过程中，又与目标船3构成碰撞危险，航向缓慢变化至64°，并在t=3 045 s 与目标船3 达到最小距离1.131 n mile；在t=3 060 s，本船迅速右转39°避让目标船4，1 305 s 后与目标船4 达到最小距离1.186 n mile；最后在t=4 905 s本船到达目标点。

由图20可知：改进APF算法在多船会遇场景下依然有航向震荡的情况，这是由于APF 算法不能从全局去认识避碰过程，只能依靠实时的碰撞危险判断来指导航向变化。由于引力与斥力的不协调动态变化，导致在某些会遇局面下避碰行动缓慢，甚至使来船不能保持在安全距离之外。相比于改进APF避碰算法，使用本文提出的基于TD3的避碰算法，在本船避让过程中航向变化快速平稳，波动较小，避碰路径光滑。由图21可知：在整个避让过程中，本船与各目标船之间的距离始终保持在安全距离4 3 n mile之外，表明提出的避碰算法在多船会遇场景下能够安全有效的指导船舶进行避让。

2）避碰成功率对比实验。为了进一步验证本文提出的避碰算法的性能，在多船会遇场景下，对船舶避碰成功率和平均避碰路径长度这2个指标与改进APF避碰算法进行比较。2种避碰算法的初始设置与多船避让仿真实验一致。

在实验中，首先生成1 张12 n mile×12 n mile 大小的实验地图，并在地图中随机添加多艘目标船，目标船初始位置的x、y坐标均从0～12 随机选取，为了让实验更真实，每生成1艘目标船，就判断与本船的距离是否大于5 n mile，若不是则删除该目标船信息并重新生成。目标船的航向通过生成各自的目标点而得到，但是目标船不会因为到达目标点而停船，目标点位置的x，y坐标从0～10 随机选取，目的是让目标船的航向更多的指向本船与本船目标点之间区域。目标船的航速大小在3～17 n mile/h 之间随机生成。另外，设置本船起点坐标（0，0），目标点坐标（10，10），船速12 n mile/h，航向45°。在生成完1张实验地图之后，本文避碰算法与改进APF 算法在实验地图中自动进行避碰，设定本船与目标船的距离小于0.25 n mile或碰撞路径长度超过30 n mile为失败，避碰结束后保留是否成功与路径长度数据。通过此方式进行1 000 次避碰实验，即生成1 000 张实验地图分别对2种算法进行验证。

为了提高实验结果的可信度，在2～4，5～7，8～10 艘目标船的情况下分别进行3 次上述实验过程，总共进行了9 000张实验地图的避碰规划，取指标平均值并记录，实验结果见表4。

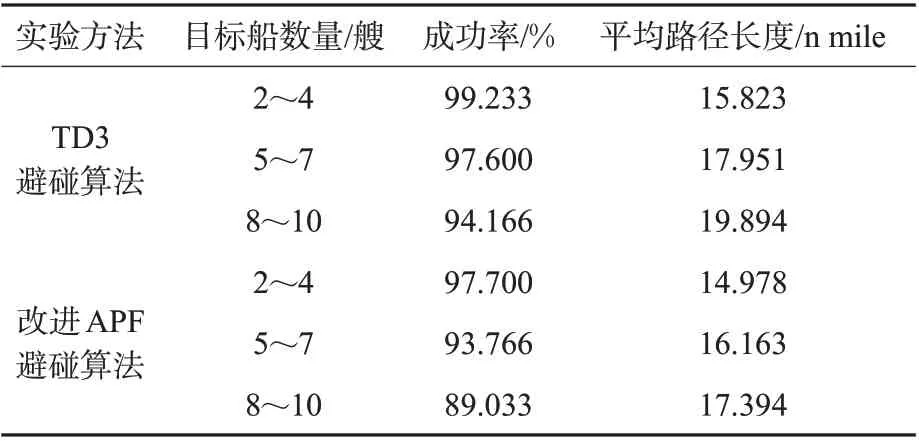
表4 对比实验结果数据表Tab.4 Comparison test results data table

由表4 可见：提出的TD3 避碰算法的船舶避碰成功率高，特别是避碰2～4 艘目标船时成功率达到了99.233%，即使在8～10 艘目标船的情况下，依旧有94.166%的成功率。而改进APF 避碰算法在3 种实验场景中均比本文算法成功率低，特别是在目标船增加到4 艘以上时，改进APF 算法的避碰性能下降严重。在避碰路径对比上，本文算法的平均路径长度要比改进APF 算法更长，这是由于本文避碰算法的输入为全局的状态信息，即使在本船没有碰撞危险时，也会关注目标船的动态，避免过快恢复航向又造成碰撞危险的产生，所以TD3 避碰算法的路径更加安全可靠，路径也会更长。

5 结束语

针对船舶自主避碰问题，基于TD3 算法提出了1种《避碰规则》约束下的、符合良好船艺的、能自主学习适应环境特点的船舶自主避碰方法。

1）提出的基于TD3 的避碰方法采用碰撞危险监测范围内的全局状态信息作为输入，保证输入神经网络中航行信息的统一性和完整性，并使用连续动作空间供算法选取避碰决策动作，具有避碰决策航向变化快、幅度大与路径平滑的特点。

2）避碰算法通过随机场景训练并融合了LSTM网络提取航行信息特征，提高了模型的泛化能力，适用于对遇、追越、交叉相遇以及多船会遇场景。

3）考虑《避碰规则》与良好船艺设计奖励函数，实现了船舶安全有效的避让目标船。避碰算法在复杂会遇场景下有较高的避碰成功率。

4）在训练中通过跳帧、随机探索、批量大小和迭代更新次数动态增大等方式加快神经网络的训练速度，提升算法稳定收敛的速度。

但是，在提出的避碰算法中船舶是作为单智能体进行避碰决策的，暂未考虑船舶间实时交互的协同避让，今后可针对多船协同避让开展进一步研究；《避碰规则》的适用场景为开阔水域，针对特定的受限水域应对船舶《避碰规则》进行改进和修正，才可以保障模型的适用性；在后续研究中增加船舶转向耦合变速的策略以及会遇局面的自动识别方法可以进一步提升模型的性能。