贯通运营下考虑运力利用均衡的城轨开行方案优化研究

童有超，王晓潮，赖坤涛，华炜欣

（广州地铁设计研究院股份有限公司，广东广州 510010）

1 研究背景

贯通运营是城市轨道交通（以下简称“城轨”）深层次网络化运营的必然选择，可有效满足跨线客流直达出行需求，缓解换乘站客流组织压力，缩短乘客出行时间，为城轨供需双方提供便利。城轨贯通运营对企业行车组织手段提出了更高要求，列车开行方案是企业行车组织的核心基础，其规定了线路在规定时段内的交路、发车频率、列车编组及停站方案，编制科学合理的贯通运营开行方案是充分发挥贯通运营模式优势的重要前提。

当前，国内外学者对贯通运营下运输组织的设计问题已展开了较为深入的研究。文献[1-3]基于乘客优先选择直达列车假设，构建了线路贯通条件下列车交路计划优化模型。但后续研究表明此行为假设与现实状况存在较大不符。为此，文献[4]提出了基于乘客直达选择偏好概率的客流分配方法。文献[5]依据出行目的对客流进行分类，并基于调研数据对分配各类客流的Logit模型进行参数标定。文献[6]构建了跨线互通下以客流总换乘次数及旅行时间综合最小为目标的混合整数规划模型，对发车频率、快车停站点进行优化。文献[7]基于多编组技术构建以发车间隔、发车频率、列车编组为决策变量，以不同编组列车间满载率最均衡为目标的开行方案编制模型。

尽管如此，既有贯通运营列车开行方案研究仍存在可优化空间，如：普遍侧重于交路及发车频率的优化，对编组方案的考虑较少；构建满载率约束公式时仍以线路区间为单位，与贯通运营下列车服务存在交叉的情景较不匹配，应基于交路区间进行构建；侧重运力利用均衡性优化的研究稍显不足。基于此，本文采用经典最优策略[8-9]方法进行客流分配，在将满载率约束公式构建细化至交路的基础上，构建优化列车交路、发车频率及列车编组的混合整数规划模型，编制考虑运力利用均衡性的最优列车开行方案。

2 问题假设与描述

2.1 问题假设

为便于抽象化描述问题，设定如下假设。

（1）1条贯通交路只覆盖2条线路，贯通运营的行车组织难度随贯通交路覆盖线路数的增加而增大，当前国内外城轨普遍只在两线之间应用贯通运营模式，如：广州市轨道交通3号线，日本机场线与箱崎线。

（2）不同交路上的车底独立运用，各交路上只开行唯一编组列车，不同交路上的列车可采用不同编组方案，不存在车底混跑的情景。

（3）乘客到站过程服从均匀分布，无乘客滞留的状况。（4）各交路上的列车均采用站站停模式。（5）各交路上下行方向列车成对开行。

2.2 问题描述

本文以“一”字型贯通线路为例对所研究问题进行抽象描述，如图1所示。“一”字型贯通线共包含2条线路，其中线路1上共有6个车站5个区间，沿上行方向分别依次对车站、区间进行编号，得车站v1，v2，…，v6、区间e1，e2，…，e5；线路2上共存在5个车站4个区间，以接轨站v6为起点，同样沿上行方向对其编号，得车站v6，v7，…，v10、区间e6，e7，…，e9。两线共存在v1，v4，v6，v104座折返站，其中v6站为双向折返站，上下行方向列车均能在此进行折返，其余车站为单向折返站，只能供一个方向列车进行折返，如车站v1，上行列车通过该站可折返至下行轨道，反之则不行。依据上述折返站位置布置，可知该贯通线路上共存在5种交路形式，分别为：v1～v6，v1～v10，v4～v6，v4～v10，v6～v10，依次进行编号，得交路1、2、3、4、5，其中交路1和交路5为本线大交路，交路2和交路4为贯通交路，交路3为本线小交路。各交路上可开行不同编组的列车，如交路1开行6辆编组列车，交路2开行4辆编组列车。基于一定约束对所有交路、列车编组类型以及发车频率进行不断地组合优化，确定最符合设置标准的组合策略，该策略即为所求的最优列车开行方案。

3 列车服务网络与路径客流分配

3.1 网络描述

线路贯通运营后，由于贯通交路与本线交路在部分区段存在服务重叠，乘客需面临多样化的出行路径选择，既有基于线路物理站点分布的列车服务网络已无法有效刻画乘客出行行为，列车服务网络构建需细化至交路层面。线路交路策略是其列车服务网络构建的核心依据，为此，本文以图1所示线路采用编号为1、4、5的交路所组成的交路策略为例，对基于交路策略的列车服务网络进行抽象描述，如图2所示。

由图2可知，列车服务网络中的节点总体上可划分为车站节点和交路节点2类，其中车站节点v1～v10的含义与前文一致，依次表示贯通线路的10个物理车站，其余节点均属于交路节点，其符号上标为所属交路编号，下标为交路所服务的车站编号，每个交路节点表示相应交路上停靠在相应车站的列车，如v11代表交路1上停靠在车站v1的列车。

同节点一样，列车服务网络中的弧总体上也可被划分为上车弧、下车弧以及运行弧3类，其中上车弧和下车弧分别表示乘客在车站的上下车行为；以节点v4与之间的上车弧为例，其前端、后端依次与交路节点车站节点v4相连，表示乘客可在v4车站乘坐交路4上的列车；而运行弧则代表着列车的区间运行过程，其两端均与交路节点相连，以首端连接末端连接的运行弧为例，其表示交路1上列车可从v3车站运行至车站v4。

3.2 路径客流分配

3.2.1 乘客出行路径

乘客出行路径是用于抽象描述乘客乘车出行轨迹的重要手段，确定乘客备选出行路径是进行服务网络客流分配的重要前提，为此，本文在考虑乘车出行行为的基础上，采用遍历算法对贯通线路各起讫点（OD）乘客的所有备选出行路径进行搜索，乘客出行行为如下：乘上直达车的乘客在后续车站不会有换乘行为；乘客不会在同一条交路上有2次及以上乘车行为，即乘客不会从交路1换乘至交路2后，在后续车站又从交路2换乘至交路1上；乘客出行换乘次数存在上限，出行轨迹覆盖线路不大于2条线路的乘客在出行时最多只换乘1次；换乘客流一般只在其已乘交路与计划换乘交路所共同服务区段的两端车站进行换乘。

以图2所示网络中OD分别为v1、v10的客流为例，在考虑上述乘客行为的基础上，通过遍历算法搜索到的路径如表1所示。

3.2.2 最优策略客流分配方法描述

最优策略客流分配是指乘客到达车站后，选择乘坐第一列开往其目的地方向的列车进行出行。以表1所示OD客流的备选路径为例，当交路1、4、5上列车发车频率均为10对/h时，其各备选路径通过最优策略客流分配方法计算选择概率的过程如下。

表1 OD为车站 、 客流的备选路径

首先，以换乘客流发生换乘行为的车站v4、v6为节点，将乘客的出行轨迹划分为3段，各段可选交路及概率如表2所示。

表2 出行轨迹划分及交路被选概率

选择路径①的客流在出行过程中只有1次换乘判断，“是否在车站v4从交路1换乘至交路4上”，故其被选中的概率为p= 1.00×0.50 = 0.50。

选择路径②的客流在出行过程中需进行2次换乘判断，“是否在车站v4继续乘坐交路1上列车至车站v6，是否在车站v6换乘至交路4上”，故其概率为：p= 1.00×0.50×0.50 = 0.25。

选择路径③的客流在出行过程中也需进行2次换乘判断，“是否在车站v4继续乘坐交路1上列车出行，是否在车站v6换乘至交路5上”，相应概率为：p= 1.00×0.50×0.50 = 0.25。

4 服务重叠交路发车频率相容性

由于贯通交路横跨2条线路，其服务范围常与本线交路在部分区段发生重叠，为保证服务重叠区段行车安全，服务交叉交路发车频率之间需具备相容性。如图3所示，当相互交叉的2条交路均以12对/h的频率均匀发车时，只需将某一交路上的列车初发时刻向后延迟2.5 min，即可保证交叉区段的行车安全；而当2条交路的发车频率分别为12对/h和10对/h时（图4），无论2条交路的列车初发时刻如何调整，交叉区段的行车间隔都无法满足安全要求。为此，本文基于实际推算，得出服务交叉交路间发车频率相容性矩阵，如表3所示（在实际中为便于行车组织，发车频率一般选取3600的除数，且为了保证城轨的竞争力，各交路的最低服务水平及车站发车总发车能力需分别不低于4对/h以及6 对/h[10]）。

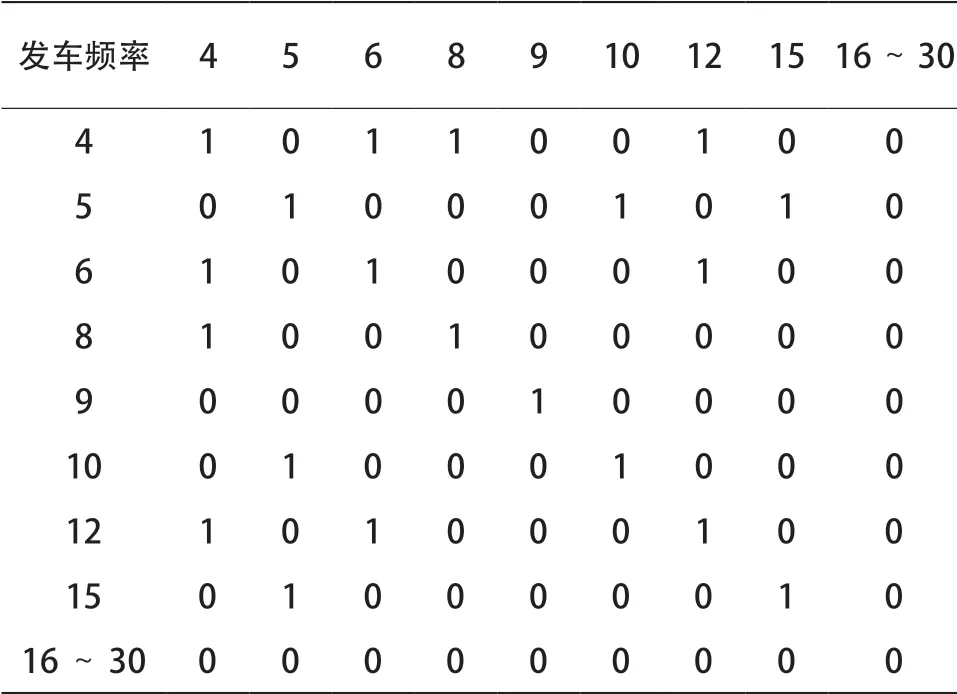
表3 发车频率相容性矩阵 对/ h

5 模型构建

5.1 符号说明

5.1.1 参数

H为研究时段的时间长度，min；R为备选交路集，R={r1，…，ri，…，rI}，I为备选交路总数；为0～1变量，当交路ri覆盖区间m时，= 1，反之则为0，M为区间标号总数；为0～1变量，当交路ri在车站v折返时，= 1，反之则为0，V为车站标号总数；li为交路ri的里程，km；Ti为交路ri的周转周期，min；a为车底单位购置成本，元/（辆· min）；g为车底单位走行成本，元/（辆· km）；B为列车编组类型集合，B={b1，…，bn，…，bN}，N为列车编组类型总数；cn为bn型编组的列车定员，人；fmin为列车最低发车频率，即线路最低客运服务水平，对/h；fmax为列车最大发车频率，即线路通过能力，对/h；Nvz为车站v的折返能力，对/h；N1为线网列车交路设置数量上限，条；N2为单一区间可覆盖交路数量上限，条；u1为列车满载率上限；OD为乘客od对集合，OD={od1，…，odj，…，odJ}，J为乘客od对总数；Qj为odj乘客的客流量，人次；MT为相容发车频率对集合，集合中每个元素为2个相容的发车频率所组成的向量。

5.1.2 决策变量

xi为0～1变量，当交路ri被选中时，xi= 1，反之则为0；fi为交路ri上的列车发车频率，对/h；为0～1变量，当交路ri采用bn型列车编组时，= 1，反之则为0。

5.1.3 过渡变量

P为路径总集（服务网络层面），P={P1，…，Pj，…，PJ}；Pj为odj客流备选路径集合，，K为odj客流备选路径总数；为分配至路径的odj客流量，人次；为路径所需的出行费用，元；为0～1变量，当路径覆盖区间m时，= 1，反之则为0；为0～1变量，当选择路径出行需乘坐交路ri上列车时，= 1，反之则为0。

线路交路策略随xi取值的变化而变化，交路策略是服务网络构建的核心依据，而服务网络是搜索乘客备选路径的重要基础，由此可知在求解过程中为变量，但其变化不具备自主性，而是由决策变量xi的取值所决定，故在此将路径列为过渡变量，其余符号所表示含义均涉及路径，故也将其纳入过渡变量序列。

5.2 目标函数

5.2.1 客流总出行费用最小

广义上，在计算乘客出行费用时，需同时考虑票价、在车时间、候车时间、换车走行时间、换乘次数5 项内容，然而在贯通运营下，由于车站换乘模式普遍为同站台换乘，且同一OD乘客备选路径集中各路径的票价、在车时间相互一致，故换乘走行时间、在车时间以及票价不会影响乘客出行行为，基于此，本文在计算乘客出行费用时只考虑候车时间和换乘次数，其中候车时间为起点站候车时间与换乘站候车时间的统称。乘客出行费用E计算公式如下。

式（1）中，θ1为时间价值，主要取决于当地经济发展水平，本文取1元/min；tow为起点站候车时间，取车站行车间隔的一半，min；ttw为换乘站候车时间，贯通运营下分2种情形，换乘至服务重叠交路时，即为该站行车间隔，换乘至衔接交路时，与起点站候车一样，取车站行车间隔的一半，min；nt为换乘次数，次；θ2为换乘次数对应时间价值的换算系数，依据既有研究[11]，本文取10元/次。

基于此，可得线路客流总出行费用，如公式（2）所示。

5.2.2 企业运营成本最小

企业运营成本主要包括车底购置成本和走行成本2项，其中车底购置成本为运用车、备用车、检修车数量之和（一般取运用车数的1.2倍）与车底单位购置成本的乘积，车底走行成本为车底走行公里与车底单位走行成本的乘积。如公式（3）所示。

5.2.3 列车满载率均衡性最优

本文以线路区间断面运力与运量的比值表示区间运力利用程度，以各区间运力利用程度的方差（公式（4））作为运力利用均衡性的衡量指标，方差越小，均衡性越优，如公式（5）所示。

5.3 约束

（1）区间全服务约束，被选中的交路组合起来需覆盖线路所有区间。

（2）行车组织难度约束，为便于企业行车组织，线网交路设置数量需满足规定上限。

（3）乘车便捷性约束，为便于乘客乘车，覆盖同一区间的交路数量需满足一定上限。

（4）线路最低服务水平约束，为保证城轨竞争力，线路各区间的列车服务水平需满足规定的下限。

（5）线路通过能力约束，各区间的列车服务水平需不大于线路的通过能力。

（6）折返站折返能力约束。

（7）交路区间断面列车满载率约束，各交路上列车满载率需满足规定的上限。

（8）决策变量有效性约束。

（9）交叉交路发车频率相容性约束。

（10）列车编组模式唯一性，各交路只开行唯一编组的列车。

（11）客流全服务约束。

5.4 求解算法

本文所建模型为多目标规划模型，无法直接求解，为此，文章首先以运力利用最均衡为目标，利用python语言编写隐枚举算法进行求解，得出最优目标值；其次，基于该目标值将运力利用均衡目标转化为约束加入模型，再次利用隐枚举算法对以乘客出行总费用与企业运营成本之和为目标的新模型展开求解，通过对运力利用均衡性目标不断放缩，生成一组帕累托（Pareto）最优隐枚举算法求解步骤，如图5所示。

6 算例

本文以北京地铁1号线与八通线所组成的贯通线路为测试案例，将实际相关运营数据代入前文所建的模型与算法中，验证模型、算法的可靠性与实用性。

6.1 算例描述

北京地铁1号线西起苹果园站（由于改造暂缓开通），东至四惠东站，全长30.4 km，共设车站23座；八通线西起四惠站，东至环球度假村站，全长23.4 km，共设车站15座，如图6所示。贯通改造后，线路原换乘端点站四惠站及四惠东站变为普通中间站，全线共设6座折返站（除端点站外不含渡线折返车站），其中古城站、公主坟站、东单站为下行折返站，下行列车可在此折返为上行；复兴门站、果园站、环球度假村站为上行折返站，可供上行列车折返为下行，各车站折返能力如表4所示。依据折返站位布置，全线备选交路集及各交路数据如表5所示。考虑到1号线与八通线站台长度最大可容纳6节编组的B型车，故贯通后线路可开行4节编组和6节编组B型2类列车。本文选取线路贯通后某周三早高峰7 : 00～8 : 00时段进行研究，该时段内上行方向客流显著大于下行方向客流，如图7所示，故在此依据上行方向客流对其开行方案进行设计。限于篇幅，省去客流OD数据展示，其他参数取值如表6所示。

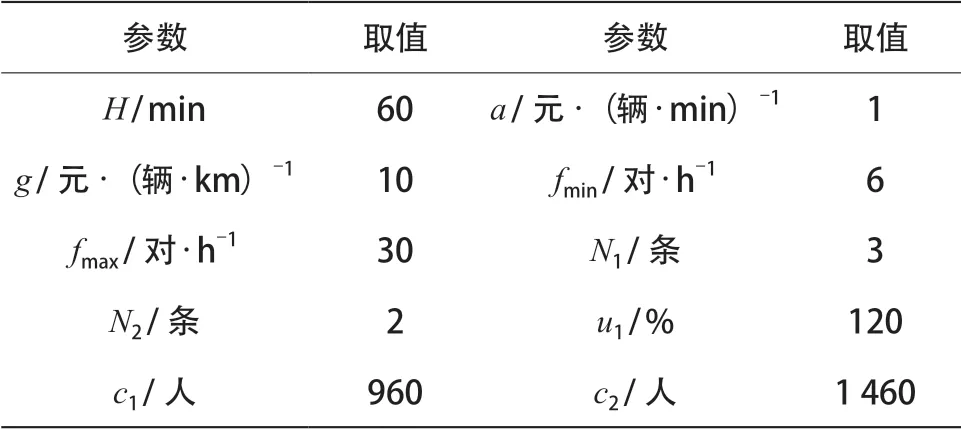
表6 参数取值

表4 折返站折返能力 对/ h

表5 备选交路集及交路数据

6.2 计算结果分析

以运力利用最均衡为目标的优化模型所编制的最优开行方案包含1、2、7号交路，各交路上依次开行5对6节编组列车、15对6节编组列车以及4对6节编组列车，如图8所示。以0.05为尺度，以0～0.5为范围，对运力利用均衡目标进行放缩，转化为新约束加入以乘客出行与企业运营费用综合最小为目标的优化模型中，编制运力利用均衡性不同偏离程度下费用最优开行方案，各开行方案的内容如表7所示。

由表7可知，在0～0.5的偏离范围内，总费用最小化模型所编制的最优列车开行方案唯一，即开行1、2、7号交路，各交路上依次开行5对6节编组列车、15对6节编组列车以及4对6节编组列车。而其余开行方案由于在运力利用方差方面最小与最均衡方案相差2.5倍，不在可接受范围之内，故本文在此不对其进行分析讨论。

为进一步剖析贯通运营下考虑运力利用均衡方案的优越机理，进一步对表7中前2个方案综合费用的各组成部分进行拆解分析，并与单线运营下的最优开行方案进行全面对比，如表8所示。

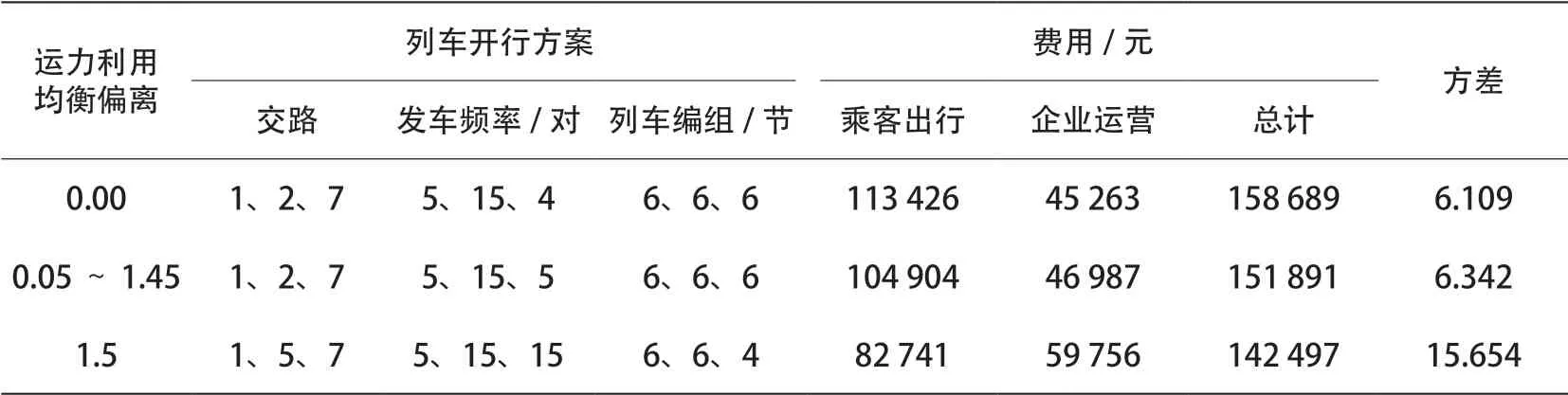
表7 列车开行方案及性能对比

由表8中带框数据可知，与单线运营相比，贯通运营能极大地改善乘客出行候车、换乘成本以及线路运力利用的均衡程度，改善幅度分别高达24.5%、55.4%、98%。而由表中加粗数据可知在企业运营成本方面，贯通运营可基本与单线运营保持一致。

表8 列车开行方案综合费用组成部分

7 结语

本文以城轨贯通运营线路为研究对象，首先提出适用于贯通运营场景下的城轨列车开行方案编制方法，与既有方法相比，该方法能较好匹配贯通线路上不同交路服务范围存在交叉的特点；其次，基于实际推算，生成能够提高贯通线路列车开行方案编制效率的服务交叉交路发车频率相容性矩阵；最后，以上述工作为基础，构建贯通运营下考虑运力利用均衡的开行方案优化模型，并基于实际线路进行算例分析，分析结果表明：贯通运营模式能够在保持企业运营成本基本不变的基础上，大幅度改善乘客出行体验以及线路运力资源利用均衡性，验证贯通运营模式的优越性。