齿间角对迷宫灌水器水力特性影响的数值模拟

张传杰，牛勇，刘逍航

(1. 中国农业科学院农田灌溉研究所/河南省节水农业重点实验室，河南 新乡 453002； 2. 山东农业大学水利土木工程学院，山东 泰安 271018； 3. 山东农业大学林学院，山东 泰安 271018)

灌水器流道普遍采用迷宫流道结构，它通过复杂的流道边界使其中的水流紊乱，从而达到降低流态指数、提高灌水均匀度的效果[1-3].针对齿型灌水器，国内外学者做了大量的研究工作.ZHANG等[4]研究发现流体在流道的上边缘附近发生逆流，在低速区域形成了不同大小的旋涡，这可能是导致通道堵塞的原因之一；OZEKICI等[5]、马炎超等[6]对齿型流道水力性能的研究表明加齿后的灌水器消能效率显著提高；GILAAD等[7]研究表明流道结构类型直接影响灌水器的流态指数；WEI等[8]研究发现灌水器中的流动滞止区是引起灌水器堵塞的最主要原因；ALI[9]，AYDIN等[10]研究表明单纯增大齿底距或者减小齿高等流道参数均可以有效提高灌水器的水力性能；ALAMOUD等[11]研究发现流道结构参数对灌水器的水力特性存在显著影响；喻黎明等[12]研究发现沙粒速度的变化取决于流道内水流运动特性，而夹角、流道宽是影响水流特性的主要流道结构参数.

文中针对不同齿间角度的正齿型和斜齿型流道结构对灌水器水力性能的影响机理进行研究，以期相关研究结论为齿型灌水器的设计和优化提供理论依据.

1 物理模型

齿型迷宫流道结构如图1所示，选取8个流道单元为研究对象.

迷宫灌水器的主要结构参数有流道宽ω、齿间角α、转角β、齿高s、通道高度H′、通道单元长度L、偏差量J、外齿宽m和齿开口宽b.所研究的灌水器流道截面为0.8 mm×0.8 mm，流道展向宽度为0.8 mm，流道总长度为19.2 mm，该长度是国内外大多数贴片式灌水器流道的长度.偏移量J设定为0.4 mm，齿高s为1.2 mm，通道高度H′为2.0 mm，通道单元长度为2.4 mm.各模型的尺寸见表1.

图1 迷宫灌水器的物理模型

表1 模型结构尺寸

2 数值模型

在数值模拟计算中，网格划分方式、网格尺寸以及计算求解湍流模型的设定对计算结果的合理性和准确性存在较大的影响[13-15].

2.1 网格无关性计算

首先采用标准k-ε模型对齿间角为60°的正齿结构(Z-2)不同网格密度的计算结果进行网格无关性的分析：采用的网格数目分别为15万、22万、29万、35万.经验证得出网格数为29万和35万时的计算结果相差仅0.2%.从计算精度和计算成本方面综合考虑，最终选用网格数为29万的网格划分形式作为齿间角为60°正齿型结构最终的计算网格，典型网格分布如图2所示.其余正齿流道结构和斜齿流道结构的网格划分参照该结构的网格划分原则划分.

图2 正齿型结构典型网格

2.2 湍流模型的确定

为了确定研究中所适用的湍流模型，分别使用标准k-ε模型、RNGk-ε模型、SST模型对计算域进行数值模拟，并将计算结果与试验实测值进行对比，如图3所示，图中Q，H分别为流量、工作压力水头.

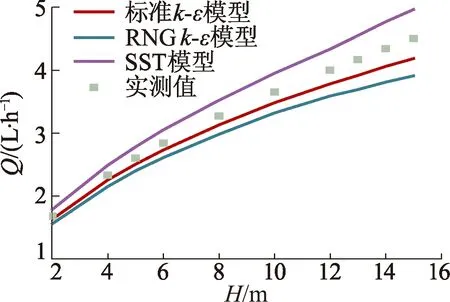
图3 不同模型计算结果与试验结果对比

从数值计算结果与实测值的吻合情况可以看出，采用标准k-ε模型计算得到的灌水器流量与实测值的偏差范围为3.1%～7.0%，RNGk-ε模型的偏差范围为7.2%～13.1%，而SST模型的偏差范围为6.3%～10.1%.可见，对于齿型迷宫灌水器的研究采用标准k-ε模型的计算结果与实际情况更加接近，因此研究中采用标准k-ε模型作为计算的湍流模型.

2.3 边界条件

进口边界条件给定为进口压力，参考灌水器中的实际压力水头值，模拟计算中给定2～15 m的10个压力水头h，即2，4，5，6，8，10，12，13，14，15 m；出口设置为压力出口，101 325 Pa；壁面采用无滑移壁面条件.数值计算采用有限体积法离散控制方程，对流项等各参数的离散采用高阶精度格式，速度和压力的耦合采用SIMPLE算法求解，收敛精度为10-6.

3 结果与分析

3.1 迷宫灌水器流场随齿间角的变化

图4为齿间角度为60°、进口压头为10 m时正齿型和斜齿型迷宫灌水器的速度矢量和流线分布.可以看出在迷宫灌水器内部，主要存在2处低速区，即齿型的左上侧低速区和齿型的右下侧低速区.

图4 齿型流道不同压头下的速度矢量和流线分布

灌水器内出现低速区域主要是由于在灌水器的内部出现回流所致，在主流区的两侧存在明显的回流旋涡；在正齿型迷宫灌水器的齿型左上侧和右下侧存在明显的大旋涡区；在斜齿型迷宫灌水器的左上侧存在明显的大旋涡区，而右下侧存在小旋涡区；斜齿型迷宫灌水器的左上侧的旋涡所占领的通道内的区域约占整个左上侧通道的50%，明显多于正齿型迷宫灌水器，而右下侧的小旋涡区所占的区域只有正齿型迷宫灌水器右下侧旋涡区域的一半左右.

图5为进口压头为10 m时，正齿结构齿间角度分别为50°，70°和80°时，灌水器内的速度矢量和流线分布图.随着齿间角度不断增大，齿型左上侧和右下侧低速区域的回流旋涡的宽度在减小，但长度在增加，旋涡外形不断变得细长.特别是当齿间角度为80°时(图5c)，低速区出现2个低速旋涡区.

图6为进口压头为10 m时，斜齿结构齿间角度分别为50°，70°和80°时，灌水器内的速度矢量和流线的变化.

对比图5和6可以看出，相比于正齿结构，斜齿结构的低速区旋涡更加明显，而且当齿间角相同时，斜齿型结构左上侧的低速旋涡区明显多于正齿型结构，而右下侧的低速区域明显小于正齿结构.随着齿间角度增大，低速旋涡所占的区域逐渐减小，主流流动更加均匀.

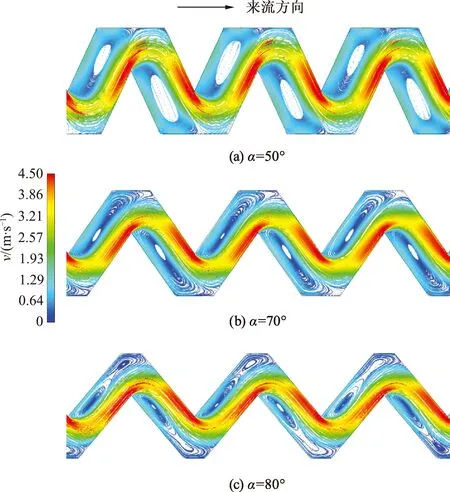
图5 正齿型流道的速度矢量和流线分布随齿间角的变化

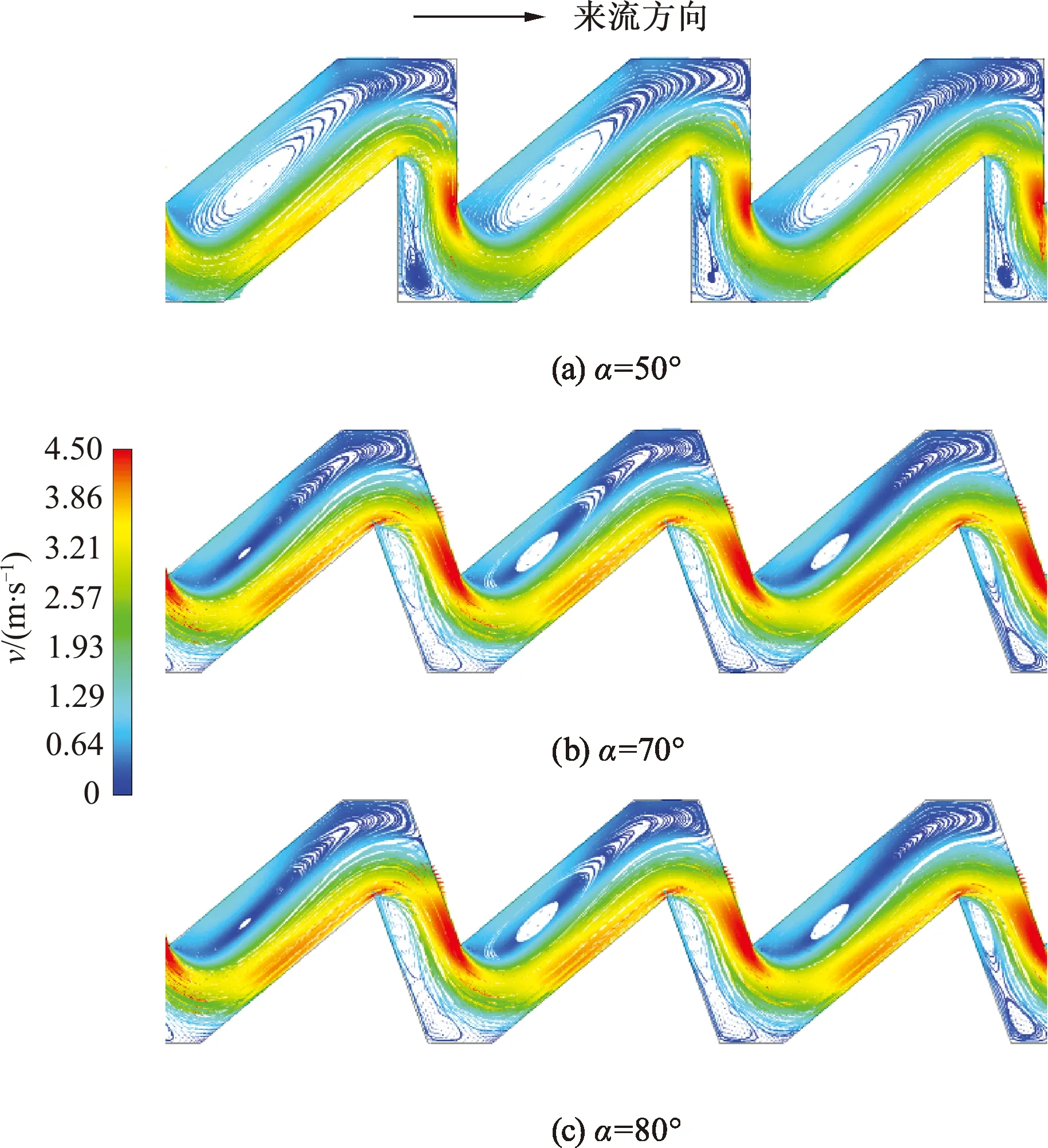
图6 斜齿型流道的速度矢量和流线分布随齿间角的变化

3.2 迷宫灌水器内流量随齿间角度的变化

图7为不同进口压力水头下，2种迷宫灌水器内的流量q随齿间角的变化情况.随着进口压头不断增大，灌水器内的流量都呈现不断增加的趋势；随着齿间角度不断增加，迷宫灌水器内的流量不断增加，而且斜齿型灌水器内的流量增加受齿间角度的影响更为明显.

图7 迷宫灌水器内流量随齿间角的变化

对于进口压头为10 m，当齿间角从50°增大到80°时，正齿型迷宫通道内的流量从3.410增加到3.700 L/h，增幅为8.6%，而斜齿型迷宫通道内的流量从2.796增加到3.530 L/h，增幅为26.3%.流量随着齿间角度增大而增加，主要是由于齿间角度增加，减小了水流在灌水器内流动方向改变的程度，减小了水流的紊流程度，流道局部水头损失系数减小，水流动能增加导致流动速度增加，从而导致灌水器内流量增加.

图8为齿间角度分别为60°和80°时，2种齿型灌水器流量随压力水头的变化.

图8 不同齿间角度下两种灌水器的流量比较

可以看出随着齿间角增大，灌水器的流量在不断增加；当齿间角度相同时，正齿型迷宫灌水器的流量大于斜齿型的；当压力水头相同时，斜齿型齿间角度的变化导致的灌水器流量的变化比正齿型更为明显.

3.3 迷宫灌水器的流量系数和流态指数

流量系数和流态指数是评价灌水器性能优劣的重要参数.模拟中的进口压力水头h和灌水器流量q应用式(1)进行回归计算.

q=khx，

(1)

式中：k为流量系数；x为流态指数.

图9为流量系数k随着齿间角度的变化，可以看出随着齿间角度增大，流量系数呈现明显增大的趋势.齿间角度从50°增大到80°，正齿型迷宫灌水器的流量系数从1.14增大到1.26，斜齿形迷宫灌水器的流量系数从0.94增大到1.18；正齿型迷宫灌水器的流量系数明显高于斜齿型的；齿间角度为50°的斜齿型迷宫灌水器的流量系数最小，为0.94，说明该结构的灌水器的流量波动最小；齿间角度为80°的正齿型迷宫灌水器的流量系数最大，为1.26，说明该结构的灌水器的流量波动最大.

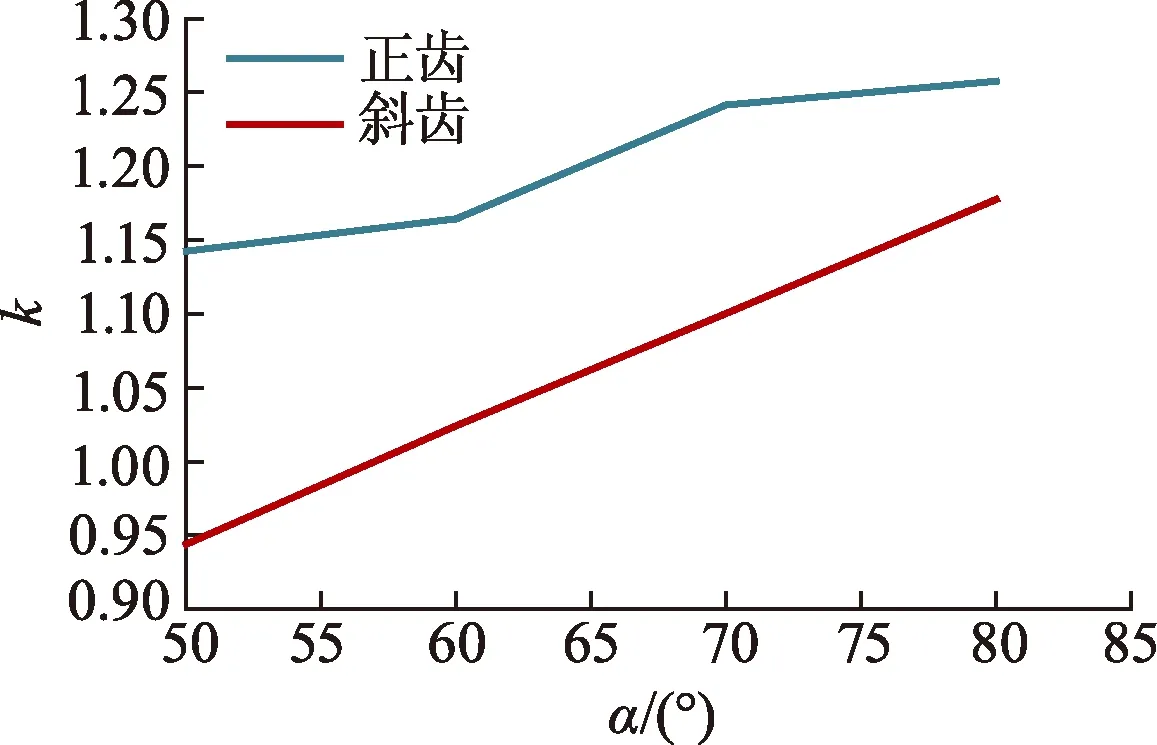
图9 流量系数k随着齿间角度的变化

图10为流态指数x随着齿间角度的变化，可以看出正齿型迷宫灌水器的流态指数明显低于斜齿型的.齿间角度为80°的斜齿型迷宫灌水器的流态指数最大，说明该结构流量对压力的变化最敏感；齿间角度为70°的正齿型迷宫灌水器的流态指数在所有灌水器中最小，为0.460，说明该结构灌水器的流量对压力的变化最不敏感，水力性能最好.

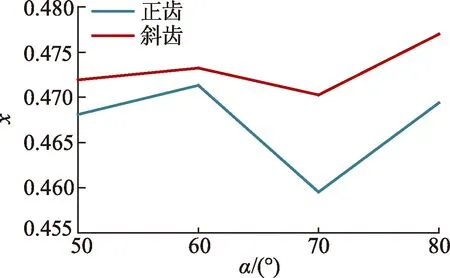
图10 流态指数x随着齿间角度的变化

从以上分析可以看出，正齿型结构的流量系数较大，流道内的流量波动性较大，但流态指数依然较小，灌水器流量对压力变化的敏感程度较低，这说明正齿型迷宫灌水器流道的水力性能较优.

3.4 迷宫灌水器的回流区

灌水器流道堵塞的主要原因是在灌水器内流通道中出现低速回流区，旋涡的出现会使流体中夹带的固体颗粒被卷入其中，极低的流速使颗粒很难回到主流，久而久之便形成沉积[16-18].对于左上侧的回流区域，2种结构灌水器都存在大旋涡，其紊流强度较大，在紊流脉动作用下固体颗粒不能保持平衡，随着流动过程的进行，进入回流区的水流与主流交汇，水流在主流区和回流区存在能量交换，因此固体颗粒沉积缓慢，不易发生堵塞现象；对于右下侧的回流区，正齿型迷宫灌水器通道存在大的旋涡，不易发生堵塞现象，而斜齿型迷宫灌水器通道内存在小旋涡，速度极低，紊流强度较小，极低的流速使固体颗粒很难回到主流，易发生堵塞，特别是右下角处最易产生堵塞现象.

4 结 论

齿型迷宫灌水器的齿间角对灌水器的水力性能存在影响，应用CFD数值分析方法，研究不同齿间角对正齿型和斜齿型迷宫灌水器通道内的流场和速度场的影响规律，得到如下主要结论：

1) 相比于RNGk-ε模型和SST模型，标准k-ε模型计算结果与试验结果更加接近.

2) 迷宫灌水器通道内存在左上侧低速回流区和右下侧低速回流区，斜齿型迷宫灌水器左上侧的旋涡明显多于正齿型迷宫灌水器，而右下侧的小旋涡区所占的区域只有正齿型迷宫灌水器右下侧旋涡区域的一半左右.

3) 随着齿间角度不断增大，迷宫灌水器内的流量不断增加，斜齿型灌水器内的流量增加受齿间角度的影响更为明显.

4) 正齿型结构的流量系数较大，但流态指数依然较小，齿间角度为70°的正齿型迷宫灌水器的流态指数在所有灌水器中最小，水力性能最好.

致谢：感谢韩启彪博士、李浩博士提出宝贵意见和建议！