基于HYDRUS对稻田不同阶段土壤水分的模拟与分析

马黎华，胡笑涛，蒋先军，王文娥*

(1. 西南大学资源环境学院，重庆 400715； 2. 西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100)

在水稻生育后期，一般要进行排水干田或自然落干的过程，稻田土壤水分状况实现由饱和态到非饱和态的转变.在这一转变过程中，土壤水分运移方式以及涉及土壤水分各平衡要素的转化均存在差异性.加深对稻田不同水分状况的认识和理解，对于农业水管理、水分高效利用以及减缓农业面源污染等方面具有实际意义.在水稻生产过程中的水量平衡要素如地表蒸发量、作物蒸腾量以及底层渗漏量等难以实现连续和有效地监测.土壤水分的数值模拟可以利用模拟结果为一些较难实现连续监测的指标提供更多的数据信息，加强对土壤水分运移过程以及环境因素影响的认识和理解.稻田的水分运移与消耗包括地表蒸发、植物蒸腾、深层渗漏和其他边界水分损失等.蒸发量与蒸腾量发生在稻田的土壤上边界，受降雨与日照气象因素的影响较为直接[1].底层渗漏量取决于土壤的水力特性、压力水头以及田块的状态[2]等多种因素.底层渗漏量占稻田水分损失总量的50%～80%[3].稻田采用干湿交替和节水控灌等不同水分管理措施会对稻田水分运移规律和稻田水分利用效率产生影响[1,4].

HYDRUS模型基于Richards方程在饱和-非饱和不同状态下的对流-弥散方程开展数值运算分析[5-6]，可以用于稻田土壤水分状况、水稻的水分利用效率和稻田氮淋失等方面的研究[1,4,7].HYDRUS在水分运移模拟过程中对土壤水力特性参数的选取至关重要，考虑到田间实际水分变化的复杂性，往往进行求逆解(inverse solution)模块对模型输入的参数进行校验，校验过程也是对土壤水分运移规律的再认识过程[1].

文中充分考虑稻田土壤水分的状态因素和作物生长情况，利用HYDRUS-1D模型，对常规水旱轮作(conventional paddy-upland rotation tillage, CT)水稻生育后期和收获后的田间水分状况进行定量分析.① 选择水稻种植后期淹水、排水干田及收获后3种不同土壤水分状况的典型阶段(阶段Ⅰ——淹水、阶段Ⅱ——排水干田、阶段Ⅲ——收获后)，使用HYDRUS-1D模型对不同土壤深度的土壤含水量进行模拟，通过试验数据率定土壤水力参数，确定模拟的有效性；② 根据水量平衡分析，估算3个不同阶段底层渗漏量的差异性；③ 根据3个不同阶段的模拟结果，分析降雨和日照时数对水稻土壤上下边界流的影响，阐明气象因素影响下土壤水分的变化规律.

1 材料和方法

1.1 试验设计

试验于2017年在重庆市北碚区西南大学稻田长期定位试验站(106°26′E，30°26′N)开展.试验站海拔230 m，年均温度为18.3 ℃，年日照时数为1 277 h，年均降水量为1 105 mm，无霜期约为334 d；土壤类型为灰棕紫色沙泥岩母质上发育的中性紫色水稻土，属于重庆地区典型丘陵紫色土稻田区.水稻品种为炳优6号(炳优6028)，为早籼三系杂交稻品种.处理CT在夏季种植水稻，收获后粉碎秸秆翻耕20 cm深；冬春季节种植油菜.

2017年试验水稻全生育期101天(5月5日移栽，8月14日收获)，第101天进行水稻收割.在水稻生长季，处理CT使表层土壤的水深保持在5 cm左右，从成熟期后期进行田间排水直至收获.降水量P、田间水分管理以及所选择的3个阶段如图1所示，图中Hw为水层深度，ds为播种后天数.选取的3个阶段分别为阶段Ⅰ(7月14—28日)，持续14 d(336 h)，稻田淹水，土壤水分为饱和状态；阶段Ⅱ(7月30日—8月13日)，持续14 d(336 h)，稻田排水干田，土壤水分从饱和状态到非饱和状态；阶段Ⅲ(8月17—24日)，持续7 d(168 h)，稻田收获后，该阶段为持续无降雨阶段，稻田土壤为非饱和状态.

在水稻生长季节和收获后收集气象和土壤含水量等相关数据.气象数据采用HOBO小型气象站(H21-USB, ONSET, America)和HOBO U30 USB气象站数据记录器(U30-NRC, ONSET, America)采集，包括降水量(mm)、日最高气温(℃)，日最低气温(℃)，日照时数(h)，地面2 m处风速(m/s).土壤含水量(体积，下同)(cm3/cm3)采用EC5土壤水分智能传感器(S-SMC-M005, ONSET, America)监测，安装在10，20，30，40和50 cm土层深度处.

图1 常规水旱轮作(CT)降雨、稻田水分管理以及三阶段选取示意图

1.2 HYDRUS模型描述

HYDRUS用于描述饱和-非饱和态土壤水分运动的方程为Richards方程，即

(1)

式中：θ为土壤体积含水量，cm3/cm3；t为时间，h；z为空间坐标，cm；K为土壤导水率，cm/h；h为压力水头，cm；S为根系吸水量，cm3/(cm3·h).

土壤体积含水量θ(h)和土壤导水率K(h)由Van Genuchten(1980)公式计算，即

(2)

(3)

式中：θs为饱和含水量，cm3/cm3；θr为滞留含水量，cm3/cm3；m，α和n为决定水分特征曲线形状的经验参数，其中m=1-1/n；Ks为饱和导水率，cm/h；l为土壤孔隙连通性参数，一般在HYDRUS模拟中选择l=0.5；Se为相对饱和度，定义为

(4)

1.2.1 土壤机械组成与水力参数确定

对于水力参数的估计采用了Neural Network Prediction模块的Rosetta Lite v.1.1[8]转换实现，主要由土壤质地即土壤的机械组成决定[6].土壤的机械组成和容重转化为6个土壤水力参数，分别为饱和含水量(θs)，滞留含水量(θr)，饱和导水率(Ks)，进气吸力倒数(α)，孔隙尺寸分布指数(n)(n大于1)，土壤孔隙连通性参数(l)取常数0.5.

分层由种植前测得的土壤分层与土壤组成，见表1，表中Hs，τ，ρ分别为土层深度、颗粒体积分数、土壤容重.表1表明，根据Rosetta Lite v.1.1得到的第2层的土壤水力参数Ks比第1层减小了27.3%.

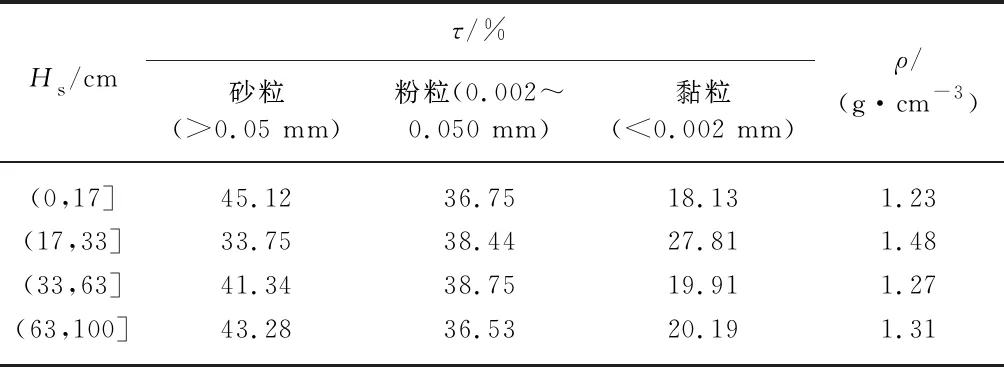
表1 水稻土的土壤机械组成

考虑到实际情况的复杂性，采用田间土壤含水量的观测数据和求逆解(inverse solution)模块，对土壤的水力参数进行参数拟合，结果见表2.

表2 土壤水分特征参数初始值以及Hydrus的优化值

在土壤水处于饱和状态的阶段Ⅰ，拟合值表明θs的拟合结果为测量数据的最大值，其他值保持初始设定不变.在非饱和阶段Ⅲ，HYDRUS的拟合值主要是关于α，n，Ks的拟合值变化，其中17～33 cm的Ks与初始值的差异最大.具体有(0，17] cm，Ks拟合值的变化范围为1.46～1.48 cm/h，在3个阶段的对比中，阶段Ⅰ略小于阶段Ⅱ和阶段Ⅲ；(17，33] cm，Ks拟合值的变化范围为1.04～1.71 cm/h，在3个阶段的比较中，阶段Ⅰ(1.04 cm/h)小于阶段Ⅱ(1.11 cm/h)，小于阶段Ⅲ(1.71 cm/h)；(33，63] cm，Ks拟合值的变化范围为1.23～1.32 cm/h，阶段Ⅱ大于阶段Ⅰ和Ⅲ.

1.2.2 HYDRUS边界条件设定

HYDRUS-1D的模拟设定为1 m深度的土壤剖面上，边界条件不考虑土壤水分的侧向流动.考虑到该区域的地下水位深度大约为3 m，底部的边界条件设定为自由排水，土壤剖面的上边界条件设定为大气边界.初始条件为每个阶段初始时刻的测量土壤含水量(cm3/cm3).

1.2.3 模型误差分析

通过计算决定系数R2和均方根误差RMSE将不同土壤深度土壤含水量的HYDRUS模型模拟值与观测值进行比较.

R2的值在0到1之间，越接近于1表明模型的模拟效果越好；RMSE与土壤含水量观测值具有相同的量纲，便于对不同阶段之间的模拟误差进行比较.

1.3 潜在地表蒸发量Ep和潜在植物蒸腾量Tp的估算方法

HYDRUS模型中的潜在蒸发量(Ep，cm/h)与潜在蒸腾量(Tp，cm/h)之和为作物的蒸发蒸腾量，以作物系数Kc[9]结合Penman-Monteith公式[10]组合计算得到[11].Ep和Tp因作物在土壤表面覆盖度差异而不同，与太阳辐射值Kgr[12]以及叶面积指数LAI密切相关，计算公式为

ETC=ET0·KC，

(5)

EP+TP=ETC，

(6)

Ep=ETC·eKgr·LAI.

(7)

水稻的叶面积指数LAI根据生育期的划分[6]实测得到：阶段Ⅰ取6.2，阶段Ⅱ取4.7，阶段Ⅲ为无植株，故LAI为0.由此得到的地表蒸发量(Ep)和植物蒸腾量(Tp)如图2所示.

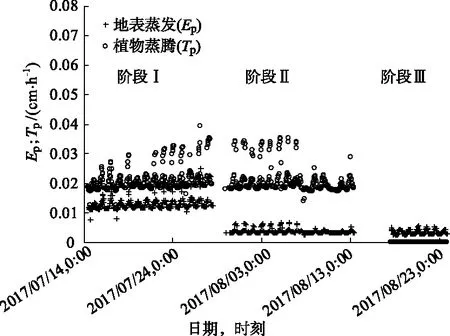
图2 常规水旱轮作(CT)稻田3个阶段的潜在地表蒸发量(Ep)与植物蒸腾量 (Tp)

1.4 根系吸水模型

在HYDRUS-1D根系吸水模块的计算中，基于利用FEDDES等[13]提出的水分胁迫响应函数.

采用SINGH等[14]优化的水稻作物[h1=100 cm，h2=55 cm，h3(高)=-160 cm，h3(低)=-250 cm，h4=-15 000 cm]的参数值作为水稻根系吸水模型的设定[6].以不同生育期实际测得的实际根系参数[15]为根系分布的输入项.

1.5 水量平衡分析

水量平衡分析计算式为

P+I=E+T+D+ΔV，

(8)

式中：P为累积降雨量，cm；I为累积灌溉量，cm(选取的阶段Ⅰ和Ⅱ无灌溉)；E为实际和累积蒸发量，cm；T为实际和累积根系吸水量，cm；D为累积底层渗漏量；ΔV为土壤蓄水量、土壤耗水或补充水量的变化，用于反映从初始时间含水量与结束时间含水量的差异.

2 结果与分析

2.1 实测土壤含水量

稻田土壤不同深度Hs的实测土壤含水量在3个选取时段的最大值、最小值和均值见表3.

表3 不同阶段不同深度的土壤含水量

在选取的阶段Ⅰ，不同深度的土壤含水量均处于饱和含水量的状态，各个土层之间的最大值、最小值和平均值的差异也很小.在选取的阶段Ⅱ，除了10 cm深度的最大值和最小值的差异不大，深度20，30，40和50 cm土层含水量的最大值接近饱和含水量0.5 cm3/cm3，最小值为0.1～0.2 cm3/cm3.在水稻收获后阶段Ⅲ中除50 cm，其他土层的含水量明显处于非饱和状态，最大值和最小值均为0.1～0.2 cm3/cm3.阶段Ⅰ，Ⅱ，Ⅲ的0～50 cm平均土壤含水量分别为0.521，0.316，0.169 cm3/cm3.选取的3个阶段基本代表了稻田土壤处于淹水饱和状态(阶段Ⅰ)、排水干田由饱和状态到非饱和态的转换过程(阶段Ⅱ)和收获后完全非饱和状态(阶段Ⅲ).

2.2 模型模拟与误差分析

稻田土壤10，30和50 cm深度土壤含水量的实测值θt和HYDRUS模拟值θm如图3所示.

在阶段Ⅰ，不同深度稻田土壤含水量的实测值均接近其饱和含水量，即0.5 cm3/cm3左右，其中10 cm深度的实测值存在微小的波动变化，各土层的HYDRUS的模拟值为一条直线，基本等于该土层的饱和含水量值；30 cm深度土壤含水量的模拟值略低于实测值，模拟值和实测值的平均值分别为0.52和0.53 cm3/cm3；50 cm深度土壤含水量的模拟值略高于实测值，模拟值和实测值的平均值分别为0.51和0.49 cm3/cm3.

在阶段Ⅱ，土壤含水量的变化范围为0.20～0.50 cm3/cm3.在变化节点附近，实际的土壤含水量的变化比模拟值减小得更为迅速.10 cm深度的土壤含水量为0.20 cm3/cm3左右，由于降水呈现2个峰值的变化，模拟值的变化比实测值的变化更加明显.30 cm在这一阶段部分仍处于饱和状态，存在饱和态与非饱和状态的转换过程，这可能与犁底层的存在或者水稻土特殊的土层结构有关.在模拟中调整压力水头可以取得较好的模拟效果，由图3b部分下降趋势中，实测值比模拟值的变化更陡.

在阶段Ⅲ，HYDRUS能够较好地模拟非饱和状态下无降雨土壤水分持续降低的过程，30 cm深度处的模拟值略高于实测值，模拟值和实测值的平均值分别为0.17和0.15 cm3/cm3.

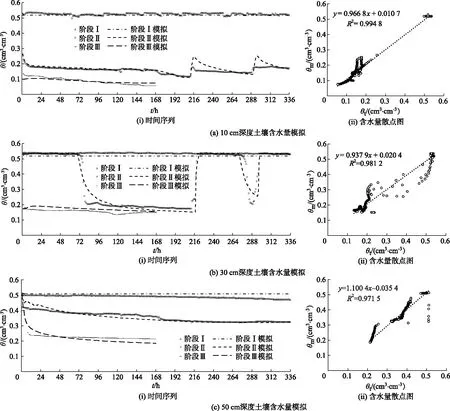
图3 稻田10，30和50 cm深度阶段Ⅰ，Ⅱ和Ⅲ土壤含水量

表4为CT在不同土壤深度、不同阶段的实测和模拟含水量的误差分析结果.除了阶段Ⅰ，R2均符合模拟值与观测值存在显著(P<0.05)线性关系.RMSE在3个阶段均为0.00～0.10 cm3/cm3.阶段Ⅰ中，除了在50 cm处，其他土壤深度处于饱和土壤含水量(0.51～0.53 cm3/cm3)中，RMSE最小(0.02).阶段Ⅱ中的R2最高(0.72)，RMSE较低(0.06)；阶段Ⅲ中的R2较高(0.65)，RMSE最低(0.05).可以认为HYDRUS可以对稻田的水分进行有效模拟，对阶段Ⅲ土壤水分非饱和状态下的模拟效果好于阶段Ⅱ和Ⅰ，即土壤水分饱和或部分饱和状态下的模拟效果.

表4 土壤含水量HYDRUS模拟误差分析

2.3 水量平衡分析与底层渗漏量估算

由式(12)，考虑不同阶段的降雨P，E，T和土壤水分变化的水量平衡结果见表5，表中d1，θa，Tp，Ep，Dc，Ds分别为天数、0～50 cm含水量均值(cm)、实际蒸腾量、实际蒸发量、底层渗漏量计算值、底层渗漏量HYDRUS模拟值.在阶段Ⅰ，水分输入总量来自降水量5.84 cm，其他补充量为3.56 cm，土壤水分损失提供为1 cm；水分损耗中，植株蒸腾量占57%，地表蒸发量占43%.在阶段Ⅱ，水分输入总量来自降水量5.26 cm，土壤水分损失提供的水分补给为5 cm；水分损耗中，植株蒸腾量占36%，地表蒸发量占12%，底层渗漏量占52%.在阶段Ⅲ，水分输入总量来自降水量0 cm，土壤水分损失提供为12 cm；水分损耗中，植株蒸腾量占0%，地表蒸发量占5%，底层渗漏量占95%.

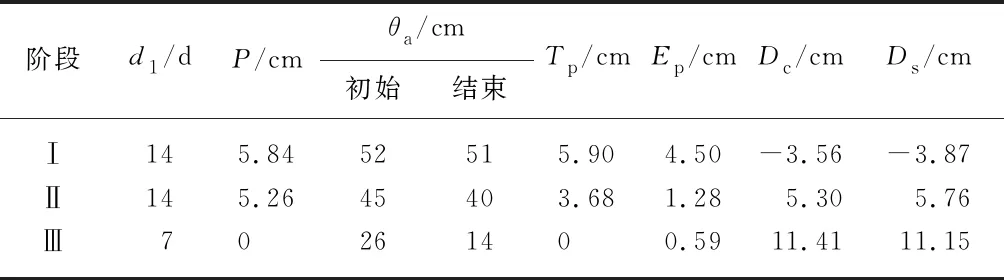
表5 常规水旱轮作(CT)稻田3个阶段的水量平衡分析

在阶段Ⅱ和阶段Ⅲ，底层渗漏量是稻田水分损失的主要来源；阶段Ⅰ以水分补充为主，阶段Ⅱ以底层渗漏为主.在阶段Ⅰ和阶段Ⅱ，土壤含水量变化不大，土壤含水量基本维持和接近土壤饱和含水量.在阶段Ⅲ，由于作物已经被移除，导致土壤含水量的变化主要有地表蒸发和底层渗漏导致，底层渗漏量是水分减少的主要方式.

2.4 HYDRUS模拟降雨、日照对土壤水分的影响

2.4.1 降雨对HYDRUS模拟上、下边界流的影响

根据HYDRUS模拟结果中对于上边界流的计算值，降雨对于上、下边界流q的影响如图4所示.降雨量的大小影响了边界流的大小.阶段Ⅰ中，3次降雨的累积降雨量分别为1.98，3.14和0.06 cm；对应边界流的变化值为-0.010～0，-0.030～-0.007和-0.007～-0.003 cm/h.

图4 降水量对上、下边界流的影响

在阶段Ⅱ，上边界流的变化依然受到降水量的影响较大，下边界流的变化受降雨量影响较小，下边界流先迅速减少然后较为稳定.

在持续无降水的阶段Ⅲ，由于缺少降水量的补给，上边界流为0，下边界流先迅速下降随后趋于稳定.

2.4.2 日照时数对HYDRUS模拟实际蒸散发的影响

根据HYDRUS的模拟结果，日照时数tsun对于实际作物蒸腾量和实际地表蒸发量产生直接的影响如图5 所示.

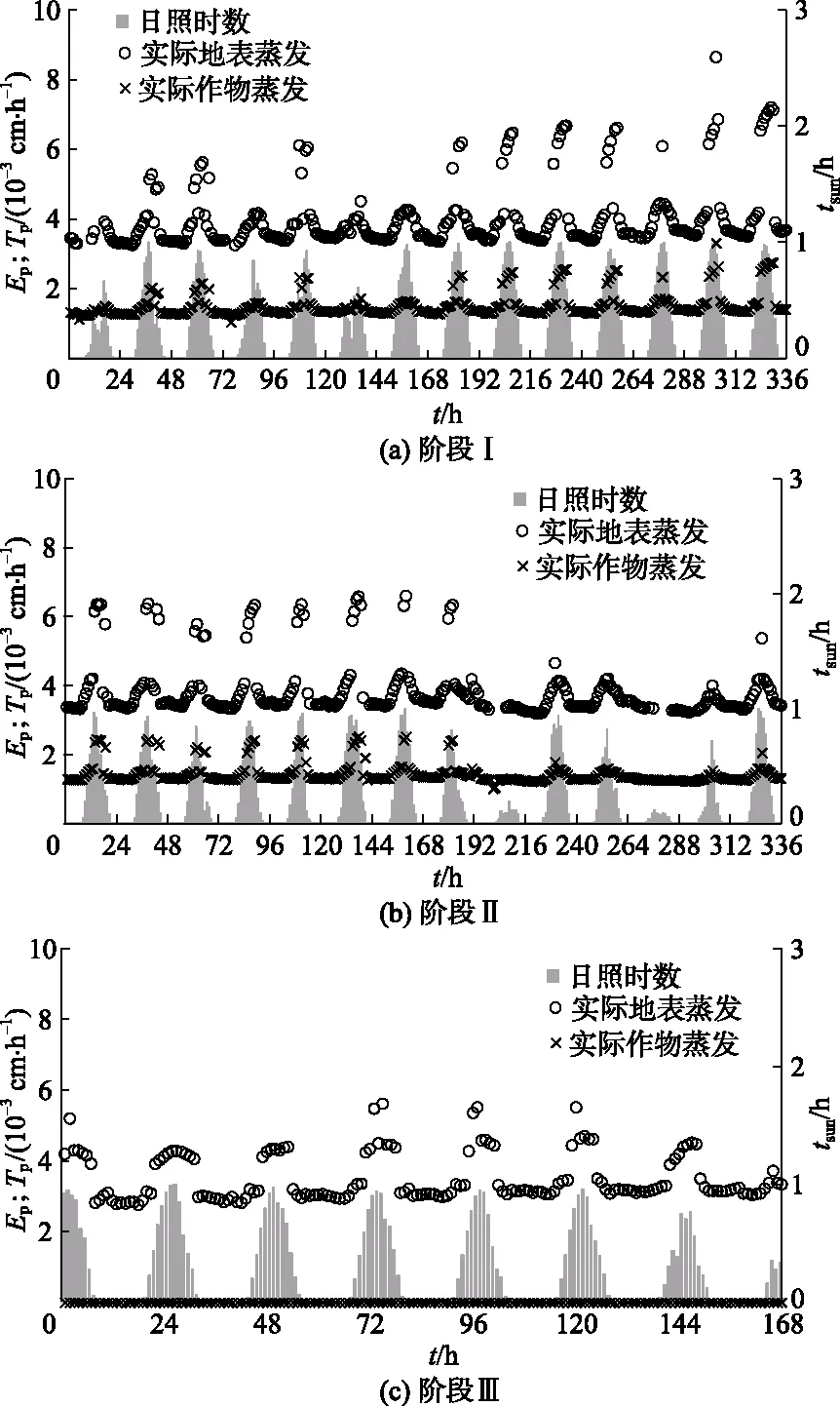
图5 日照时数对于实际作物蒸腾量和实际地表蒸发量的影响

由图可以看出，日照时数的日变化规律导致了实际作物蒸腾量和实际地表蒸发量也呈现了明显的日变化规律.总体上，阶段Ⅱ的蒸发蒸腾量低于阶段Ⅰ.在阶段Ⅰ和Ⅱ，对应日照时数最大的正午，实际作物蒸腾量和实际地表蒸发量最大值分别为0.006和0.003 cm/h；对应日照时数为0的夜间，实际作物蒸腾量和实际地表蒸发量最小值分别为0.003和0.001 cm/h.在阶段Ⅲ，实际作物蒸腾量均为0，对应日照时数最大的正午，实际地表蒸发量最大值为0.005 cm/h；对应日照时数为0的夜间，实际地表蒸发量最小值为0.003 cm/h.阶段Ⅲ的地表实际蒸发介于阶段Ⅰ和Ⅱ之间.

3 讨 论

不同阶段稻田土壤水分的差异来源之一体现在土壤水力特性参数的差异上.文献[16-17]证实了HYDRUS反推模块在实际使用中的有效性.文中(见表2)以Ks的差异为例，0～17和17～33 cm 2个土层的Ks均为阶段Ⅰ的小于阶段Ⅱ和Ⅲ的，即在饱和态到非饱和态的转变过程中，Ks是逐渐变大的，这与土壤自身饱和-非饱和入渗的规律具有一致性[18].Ks的变化由阶段Ⅰ的1.04 cm/h和阶段Ⅱ的1.11 cm/h，变为阶段Ⅲ的1.71 cm/h.在图3的结果中也可以看到30 cm的土壤水分在阶段Ⅱ中处于饱和与非饱和态交替变化中.在分层交界面，当分层土壤水力特性差别较大时，土壤入渗规律存在变化上的复杂性[17].

稻田水量平衡要素的差异很大程度上取决于降水量和灌溉量的差异[6].文中研究中选取水稻生育后期，不考虑灌溉因素，水量平衡要素的影响主要来自于降水量与土壤水分变化，以及底层渗漏量的差异上.由图4可知，在假设不产生地表径流的前提下，降雨过程与上边界流和下边界流的变化密切相关；而阶段Ⅱ和Ⅲ中的变化更接近非饱和土壤的变化，即先迅速降低然后趋于平衡的变化[17].日照对于3个阶段的影响也存在一定的差异性.由图5所示，对地表实际蒸发量而言，阶段Ⅲ中，日照时数的变化与地表实际蒸发量关系的决定系数为0.83，阶段Ⅰ和Ⅱ的该值分别为0.64和0.61.根据HYDRUS这一模拟结果，可以认为在水稻收获后的阶段Ⅲ，稻田土壤的地表实际蒸发量与日照时数的关系更密切.

4 结 论

1) HYDRUS可以实现对稻田不同水分状态3个阶段土壤含水量的有效模拟.

2) 根据水量平衡结果，阶段Ⅰ稻田土壤水分以水分补充为主；阶段Ⅱ和Ⅲ的土壤水分以水分损失为主，底层渗漏量是水分损失的主要途径，分别占总水分损失的52%和95%.

3) 降雨是土壤上边界流发生变化的直接原因，日照时数为蒸发蒸腾量带来了日变化规律.