基于模糊几何加权模型的灌区水资源优化配置

汪恩良，胡胜博，田雨，刘兴超*

(1. 东北农业大学水利与土木工程学院，黑龙江 哈尔滨 150030； 2. 黑龙江省寒区水资源与水利工程重点实验室，黑龙江 哈尔滨 150030)

水资源短缺是一个与社会经济和全球可持续发展相关的问题，随着人口的增长和经济的快速发展，水资源短缺形势会愈来愈严峻[1-2].预计2050年全球人口将增长到95亿人，届时粮食需增产60%、农业用水量需增加19%，才能满足基本粮食需求[3].农业是国民经济发展的基础，农业水资源是农业生产和粮食安全的核心战略资源.根据《2019年中国水资源公报》统计，全国的用水总量为6 021.2亿m3，其中农业用水3 682.3亿m3，占用水总量的61.16%.

在水资源紧缺的背景下，灌区却受诸多因素影响而造成水资源浪费，例如灌溉制度不合理、管理不到位及灌水设施老旧等，将进一步加剧农业生产的困境.灌溉用水是灌区水资源消耗的主要途径和保证粮食安全生产的重要手段[4]，因此，合理配置农业水资源、提高农业水资源利用效率，对保障区域粮食安全和实现社会经济的持续发展具有极其重要的意义[5].

灌区水资源优化配置被证明是实现灌区高效用水的有效方法，即：在整个灌溉季节，将灌区可利用的、有限的水资源，在时、空上进行合理的分配，获得最优配水方案[6].

灌区水资源优化配置需要权衡多方面利益，涉及经济、社会和生态环境等多方面，BURAS[7]在1972 年引入、应用了线性规划方法与动态规划方法到水资源领域.PERCIA等[8]以最大经济效益作为目标函数，兼顾考虑水质要求的情况下，建立了不同用水部门的多水源系统优化模型.付强等[9]将实码加速遗传算法与多维动态规划法相结合，建立了遗传动态规划模型，解决了多维动态规划法在求解作物非充分灌溉下，灌溉制度优化过程中的反复试算、易早熟及陷入局部最优而难以求得全局最优解的问题.宋朝红等[10]通过对非充分的灌溉条件进行研究，构建了水资源非线性规划配置模型，用以对作物的灌溉制度进行优化，模型以混合遗传算法中的十进制编码进行求解.陈南祥等[11]以作物产量最大、农作物缺水量最小为目标进行优化配水，并构建了灌区的多水源、多目标优化模型，以获得灌区不同水平年的最优化的水资源配置方案.陈红光等[12]提出基于区间两阶段鲁棒优化模型，通过调整种植结构以促进农业水资源的高效利用.

目前，常见的多目标方法有模糊多目标规划法[13-14]、遗传算法[15]、粒子群算法[16]、人工鱼群算法[17]等，由于具有较强的操作性和灵活性，至今仍被广泛应用于各个领域.但以往的研究工作往往忽略或者无法有效处理灌区水资源优化配置中，各种因素导致各目标赋权存在不确定性.文中通过构建基于模糊几何加权法的灌区水资源优化配置模型，并通过灌区综合能力评价体系，以确定灌区水资源优化配置方案.

1 模型建立及求解

1.1 模型建立

针对灌区水资源优化配置过程中存在赋权的不确定性，构建基于模糊几何加权法的灌区水资源优化配置模型，在满足供水约束、水量平衡约束、作物需水量约束等条件下，可以通过改变权重，以平衡经济效益与用水量之间的关系，合理高效地配置有限的水资源.具体如下.

1) 经济净效益目标函数为

(1)

灌溉用水量函数为

(2)

式中：M为作物的市场单价，元/kg；WUEA为多年平均毛灌溉水分生产率，kg/m3；Xt为t生育期间的配水量，m3；N为灌溉水价，元/m3.

2) 将目标函数统一表示成极小化问题.

目标函数一为

(3)

目标函数二为

(4)

3) 约束条件.

供水约束为

Xt≤Qt+qt-1，

(5)

非负约束为

Xt≥0，

(6)

水量平衡约束为

qt-1=Qt-1+qt-2-Xt-1，

(7)

用水量标准约束为

(8)

式中：Qt为t生育期间的最大可供水量，m3；qt为t生育期间的余水量，m3；Wmin，Wmax分别为灌溉需水量的下、上限值，m3.

1.2 模型求解

多目标规划的标准形式[18]为

(9)

式中：f(x)=(f1(x),f2(x),…,fm(x))为m(m≥2)维目标函数；s.t.x∈X为约束条件.

利用模糊方法求解多目标规划问题时，通过在相同约束条件下确定每个目标的隶属函数μ(fi(x))，i=1,2,…,m；然后定义λ为最大满意度[19]，使之满足

(10)

即等价于以下的单目标规划问题：

(11)

(12)

首先要确定μ(fi(x))(i=1,2,…,m)，求解单目标非线性规划问题.

(13)

设单目标规划问题的最优解为fi，min，假设fi，min>0，并且设弹性满意区间为(-∞,fi,min+βifi,min)，则fi(x)的隶属函数可取为

(14)

式中：βi为第i个目标的弹性程度.

引入变量λ，将目标函数通过隶属函数转化成约束条件，与原有函数的目标函数构成一个单目标函数：

(15)

根据上述原理，将所构建的多目标模型转化成单目标模型.

目标函数为

(16)

约束条件为

-f1(x)+λ1β1f1,min≥-f1,min+β1f1,min，

(17)

f2(x)+λ2β2f2,min≤f2,min+β2f2,min，

(18)

0≤λt≤1,t=1,2,…,T,

(19)

Xt≤Qt+qt-1，

(20)

Xt≥0，

(21)

qt-1=Qt-1+qt-2-Xt-1，

(22)

(23)

式中：f1,min，f2,min为目标函数一、二的最小值.

通过Lingo软件求解该单目标函数，通过修改各个目标函数的权重，得到不同条件下的最优灌溉供水方案.

由于人为修改灌水量与经济权重的大小缺乏科学性和客观性，因此建立灌区综合能力评价体系.从经济、社会、环境出发，既要考虑灌区系统自身的层次结构，又要考虑评价目标本身属性的特征以及各个特征之间的联系[20]，确定评价指标.

文中选取熵权法.该方法把指标特征值进行计算，以确定指标的权重，避免了权重选取的主观性的影响，消除了人为干扰因素，使评价结果更加真实.步骤如下.

(24)

式中：xij为第i个方案下第j项指标.有n个待评价方案，m个评价指标，对各指标进行标准化处理，使其指标能够计算与比较.

对于正向指标，其公式为

(25)

对于逆向指标，其公式为

(26)

标准化后的规范矩阵为

(27)

计算指标信息熵ej：

(28)

k=1/lnn,k>0，

(29)

(30)

计算指标权重：

(31)

计算方案的综合得分：

(32)

根据对比方案综合得分，确定灌水量目标和经济目标的权重，得到最优配水方案.

2 实例研究

2.1 研究区概况

绰尔屯灌区位于黑龙江省杜尔伯特蒙古族自治县，嫩江干流左侧.年平均降水量为420 mm，年平均蒸发量为1 739.8 mm，属温带大陆性季风气候.土壤以草甸土和草甸黑钙土为主，有机质含量高，适宜发展水稻生产，灌区内主要作物为水稻，在水稻种植期间灌区可供灌溉用水总量为6 256.00万m3，其中水稻泡田期、返青期和黄熟期的腾发量都较小，且期间水资源充足，配水量为1 904.95万m3.因此，主要考虑水稻分蘖期、拔节期、抽穗期、乳熟期的水资源优化配置.

该灌区提引嫩江水灌溉，设计灌溉水田面积为4 533 hm2，灌溉水资源总量丰富，但在时间上，可供灌溉水资源分布不均.由于工程管理不到位且缺乏合理的灌溉制度，采用大水漫灌的灌溉制度，受建设时期资金及技术条件限制，建设标准较低，渠系水利用率低，灌溉用水量大，种植成本高，时常发生农户用水纠纷，水资源浪费严重，灌溉面积难以扩大.为了适应现代化农业高产、稳产及节水的要求，根据灌溉用水量需求和经济发展需求，优化灌区水资源配置.绰尔屯灌区地理位置示意如图1所示，图中h为高程.

图1 绰尔屯灌区地理位置示意

2.2 数据来源

根据《黑龙江省杜尔伯特绰尔屯灌区节水配套改造项目》[21]及灌区内多年降水量和径流统计资料[22]，灌溉设计保证率为75%，选取1984年为典型年，得到灌区可供灌溉用水总量为6 256.00万m3、水稻生育期可供灌溉用水量Qsu、单位水量用水成本C及水稻市场单价PU；通过黑龙江省地方标准《用水定额》[23]，得到水稻单位面积最大灌溉用水量和最小灌溉用水量.单位面积最大和最小灌溉用水量分别与水稻种植面积相乘，得到水稻灌溉需水量的上、下限值Qnu和Qnl.基础数据见表1.

表1 水稻不同生育期可供灌溉用水量与标准定额

2.3 结果分析

将可供灌溉用水量、水稻用水量标准定额及社会经济数据等输入模糊几何加权灌区水资源优化模型.由于βi表示第i个目标的弹性程度，随机对β1和β2取值，并根据最大满意度λi随权重变化情况，对β1和β2组合取值进行修改，利用Lingo软件对上述优化模型进行求解，得到不同β1和β2组合下不同权重在不同生育期的最优配水量D.以β1=β2=0.2为例，结果见表2，表中WI，WE分别为灌水量权重、经济权重.

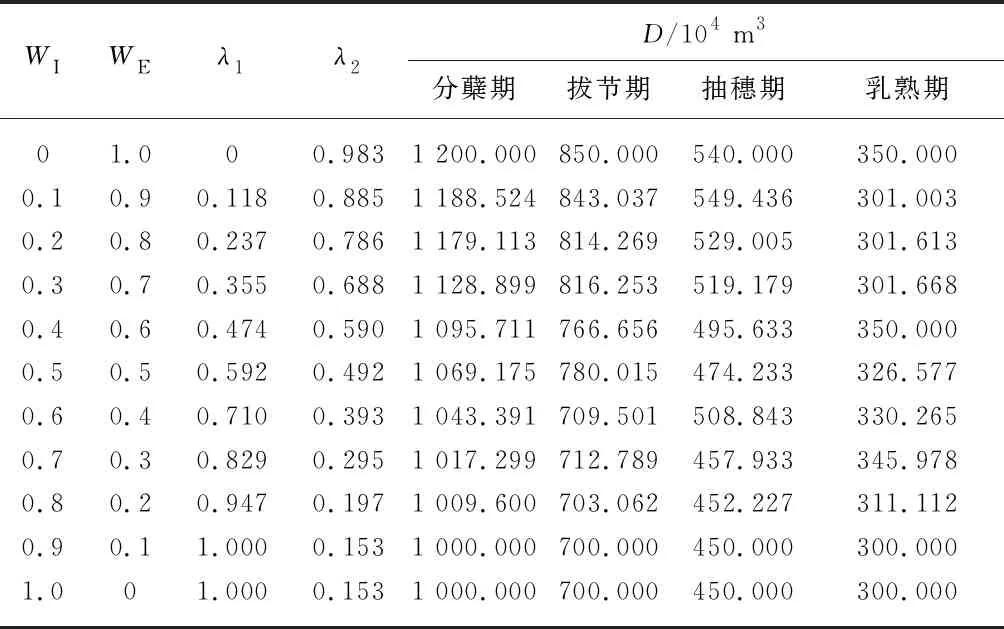
表2 β1=0.2和β2=0.2组合下不同权重在不同生育期的最优配水量

由表2可得，灌水量权重0和经济权重1.0到灌水量权重0.9和经济权重0.1，随着灌水量权重增加、经济权重减小，最优配水量的取值向目标函数二f2(X)的最优解靠近，说明灌水量权重和经济权重的大小确实代表了对不同目标的不同重要程度.但是灌水量权重0.9和经济权重0.1到灌水量权重1.0和经济权重0，最优配水量的取值即为目标函数二f2(X)的最优解，最优配水量并不随权重变化而变化，说明β1和β2组合选取得并不合适.通过将β1和β2进行组合，以分析不同权重下最优配水量的变化、得出最优配水量随权重变化的情况，如图2所示.

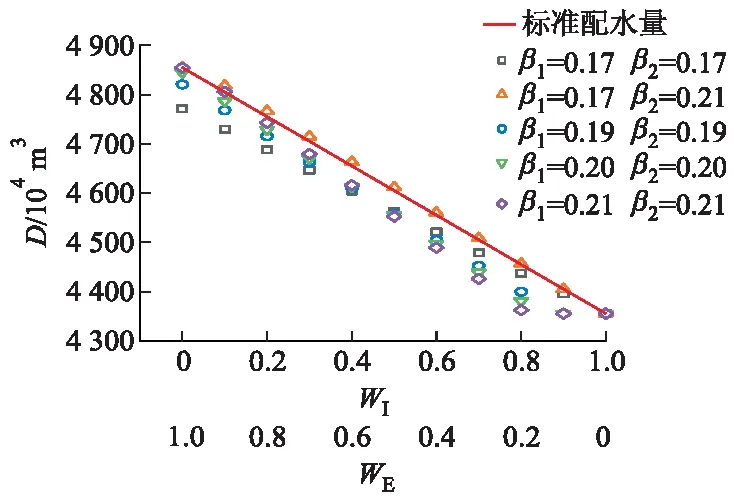
图2 不同β1和β2组合下最优灌水量随权重变化

从图2中可以看出随着β1和β2变大，最优配水量的变化区间也逐渐增大.当最优配水量随各目标权重变化呈线性变化时，即为图中的标准配水量，此时的β1和β2即能满足通过改变各个目标函数的权重，得到不同条件下的最优灌溉供水方案.

根据数据结果发现，当β1=0.17和β2=0.21时，最优配水量的变化最接近标准配水量，并且通过普通的模糊多目标规划模型求解该多目标函数所得最优解，与模糊几何加权灌区水资源优化模型所得最优解相比，如图3所示，图中E为经济效益.

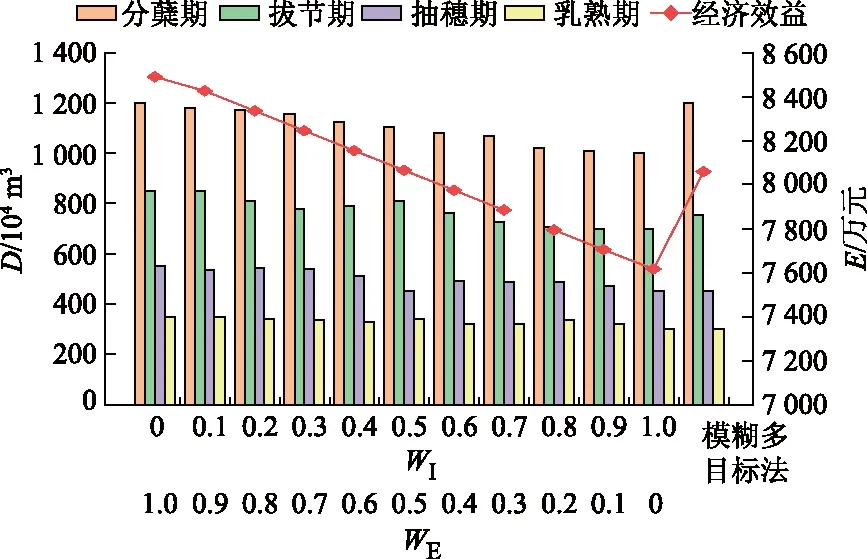
图3 β1=0.17和β2=0.21组合下模糊几何加权法与模糊多目标法的最优配水量对比

在满足约束条件下，2种方法都能够得到灌区水资源多目标规划问题的非劣解，但模糊几何加权灌区水资源优化模型所得的最优配水量随权重改变而变化.当灌水量权重为0、经济效益权重为1.0时，能够创造8 490万元的经济效益；当灌水量权重为1.0、经济效益权重为0，水稻分蘖期、拔节期、抽穗期、乳熟期的用水总量为2 450万m3.通过对权重的修正，能够得出该条件下的最优配水方案，充分考虑了各个目标的不同重要程度.而且通过分蘖期、拔节期、抽穗期、乳熟期的最优配水量对比，可以发现模糊几何加权法在灌水量权重为0、经济效益权重为1.0，到灌水量权重为0.1、经济效益权重为0.9时，先保证了拔节期和乳熟期的灌水量，减少了分蘖期和抽穗期的灌水量；在灌水量权重为0.1、经济效益权重为0.9，到灌水量权重为0.2、经济效益权重为0.8时，保证抽穗期的灌水量，减少了拔节期、抽穗期和乳熟期的灌水量.通过这种模式循环往复，以保证灌水量和经济效益随权重变化而变化，相较于普通的模糊多目标规划模型只减少抽穗期和乳熟期的灌水量这种单一的模式，更符合实际情况；模糊几何加权模型可以根据整体规划，结合投资成本和种植条件等因素，有倾向性地制订农业种植计划.

从灌区经济效益、社会效益、环境效益出发，选取水稻产值Vr(水稻产量×价格)、可增加灌溉面积A(余水总量/每公顷配水量)、配水量变化率τ[(配水量-标准定额)/标准定额]、人均水稻产量Ypa(水稻产量/人口)、化肥用量F(单位面积化肥用量×种植面积)为评价指标，通过公式(24)—(32)确定各评价指标的权重.表3为评价体系数据.

表3 绰尔屯灌区农业水资源综合能力评价体系

绰尔屯灌区农业水资源综合能力评价指标权重计算结果：化肥用量、人均水稻产量、水稻产值、可增加灌溉面积、配水量变化率的权重分别为0.217 2，0.201 1，0.201 1，0.227 7，0.152 9.

根据熵权法对指标赋权，得出不同方案的优化结果Sj，见表4.

表4 绰尔屯灌区农业水资源综合能力评价结果

从表4评价结果中可以看出，灌区农业水资源综合能力评价处于0.444 9～0.562 2，其中灌水量权重为0.3和经济权重为0.7时，在所有方案中评价结果最优，而灌水量权重为1.0和经济权重为0时，评价结果最低.

因此，当灌水量权重为0.3和经济权重为0.7时，由图3可知，模糊几何加权法模型的优化结果为分蘖期、拔节期、抽穗期、乳熟期灌水量分别为1 154.56万、779.12万、539.45万、336.57万m3，经济效益为8 245万元.由于在水稻种植期间灌区可供灌溉用水总量为6 256.00万m3，其他时期配水量为1 904.95万m3，因此能够节约水资源1 541.35万m3.从余水量观察，若把节省下来的水资源用于农业灌溉，可增加灌溉面积1 480 hm2，将产生更多的经济效益；如果将节省下来的水资源用于生态修复和森林种植，也可促进研究区域生态可持续发展.在实际生产过程中，决策者可以根据实际情况例如种植成本、整体规划、经济净效益等因素，通过基于模糊几何加权法的灌区水资源优化配置模型并结合灌区综合能力评价体系，制定最优的灌溉供水方案.

3 结 论

1) 针对灌区水资源优化配置中存在的权重不确定性问题，将模糊几何加权法和灌区综合能力评价体系结合，构建了模糊几何加权灌区水资源优化模型.以黑龙江省绰尔屯灌区农业水资源配置为例进行了研究.经过模型优化后，能够节约水资源1 541.35万m3，而且不是单一地减少某一生育期配水量.根据权重的变化，各个生育期配水量变化平稳，证明了模糊几何加权法在灌区水资源优化配置方面的可行性和优越性.

2) 对比模糊几何加权法和普通多目标优化模型的优化结果，表明模糊几何加权法可以在权重不确定的情况下提供多种优化方案，对灌区的用水总量和经济效益两者之间进行了充分的权衡，为决策者在优化灌区水稻灌溉制度时提供了理论依据和决策支持.

3) 从灌区经济效益、社会效益、环境效益出发，建立农业水资源综合能力评价体系，通过熵权法对评价指标进行加权，避免权重确定的主观性，客观、全面地对模糊几何加权法的优化结果进行评估.评价结果表明，灌水量权重为0.3和经济权重为0.7最优，水稻产值为8 245万元，分蘖期、拔节期、抽穗期、乳熟期灌水量分别为1 154.56万、779.12万、539.45万、336.57万m3，可增加灌溉面积为1 480 hm2.