基于颗粒离散元的土质路基高边坡破坏机制研究

于 超

(诚合瑞正风险管理咨询有限公司，北京 100855)

边坡问题一直困扰着岩土工作者，由于长期的地质运动、强降雨及人工扰动等，我国每年在滑坡治理方面花费大量人力、物力。如利国利民的南水北调工程，在治理边坡过程中花费巨大[1]；西部大开发工程，边坡灾害频发，严重影响工程进度及生命安全[2]。大量学者从理论研究、现场监测、模型试验、数值模拟等方面试图揭示土质边坡的破坏机制，以期提前预警。黄润秋等[3]建立了大型的室内模型试验，研究不同降雨强度下诱发滑坡机理，通过监测边坡内部含水率、孔隙水压，揭示了降雨入渗作用极大诱发边坡滑动。詹良通等[4]通过离心模型试验研究了边坡破坏特征，研究发现，对于粘性土边坡，破坏往往先出现在坡脚处，继而边坡中部发生剪切滑移，边坡上部出现拉裂隙，边坡整体滑移。对土质边坡模型的数值模拟目前大量采用有限元法[5-7]，将土体材料视为连续材料，再划分为块体进行安全性计算，可得到边坡的位移场及应力场等。部分学者采用有限差分法[8]对土质边坡模拟。部分学者[9-11]采用颗粒离散元PFC2D模拟土质边坡滑坡过程。本文基于颗粒离散元软件从细微观、宏观及大变形层面揭示土质边坡破坏机制，并分析小河段边坡滑坡破坏特征及运动特征。

1 颗粒离散元理论

颗粒离散元PFC理论中，模型由三部分组成(颗粒单元、接触单元及墙单元)。颗粒单元有不考虑变形的圆球颗粒(ball)、不考虑变形考虑形状不规则性的刚性簇单元(clump)以及既考虑变形破坏又考虑形状的不规则性的柔性簇单元(cluster)。

颗粒离散元理论中，颗粒或簇单元之间满足牛顿第二定律；接触(颗粒与颗粒接触，颗粒与墙单元接触)之间需满足力-位移准则。

1.1 力-位移准则

颗粒离散元模型中，作用于接触模型的力由切向接触力和法向接触力组成:

(1)

(2)

(3)

1.2 运动法则

根据运动法则，可建立颗粒平移和旋转运动方程：

(4)

(5)

颗粒在上一时步的力的作用下产生位移，结合力-位移准则及接触的本构模型计算得到作用于颗粒上的新的合力及合力矩；通过平行加速度及角速度与合力及合力矩关系，得到颗粒更新后的位置及旋转信息，如此反复计算，实现模型的大变形破坏[12]。

2 工程概况

京港澳高速公路小河段路基高边坡剖面见图1所示。小河段路基高边坡处于构造剥蚀重丘区地貌，路基高边坡自然坡角约 15～25°，各岩土层分布及岩土特征：

图1 边坡剖面示意图

(1)粉质黏土，黄褐色，褐红色，稍湿，硬塑，含少量铁锰氧化物，局部含少量碎石，上部 0.3 m为耕植土，含少量植物根系，揭示层厚 2.0～3.9 m。

(2)强风化片麻岩，灰褐色，褐黄色，强风化，变晶结构，片麻状构造，矿物成分主要为石英、钠长石及白云母等，原岩结构大部分破坏，矿物成分显著变化，风化裂隙发育，岩芯呈碎块状、饼状，手捏易成粉末。本路段广泛分布，揭示层厚 3.1～4.2 m。

3 模型细观参数确定

通过PFC2D双轴试验确定土质边坡细观参数，具体过程如下：以宏观参数粘聚力及内摩擦角为基准，采用接触粘结模型进行双轴试验，确定细观参数接触模量、法向接触强度、切向接触强度及摩擦系数。细观参数接触模量与宏观的土体弹性模型取一致。

双轴试验围压分别为50、150及300 kPa，得到拟合试验的破坏主应力线，标定得到的细观参数为：接触模量，40.0 MPa；法向接触强度，112.9 kPa；切向接触强度，87.9 kPa；刚度比1.0；摩擦系数0.24。试验过程及不同围压状态下试样剪切破坏形态见图2。

图2 不同围压下双轴试验

岩土体数值模拟试验与室内试验得到的宏观参数见表1，两者相差极小，说明采用颗粒离散元模拟路基高边坡可行。

表1 岩土体宏观参数及DEM试样力学参数对比

4 路基高边坡颗粒离散元模型建立

考虑到实际工程高边坡复杂性，合理简化几何形状，建立长68.5 m、宽39.5 m，坡率与实际边坡相符的数值模型。通过现场勘察，高边坡破坏主要集中于上覆粘性土层，基岩无破坏，综合考虑颗粒离散元计算效率，以墙单元代替基岩，其强度赋予岩石接触参数，以还原基岩与粘性土接触。坡脚为自由边界，相对于土体，基岩强度较大，不考虑岩体变形，接触界面处土体达到极限强度，发生滑动。高边坡的轮廓线采用CAD绘图软件1∶1绘制，通过编制程序导入颗粒离散元软件，还原实际工程边坡的几何形态和力学状态。基于工程区域降雨情况，并考虑数值模型计算效率，本文研究短期强降雨工况，其降雨强度为25 mm/h、降雨持时为2 h。本文通过对土层的强度进行折减来考虑降雨对土体的影响。不同时刻土体宏观强度及数值模拟相关强度见表2所示。

表2 不同降雨时刻宏观参数及细观力学参数

为定量反映高边坡在整个滑动过程中的力学规律和位移响应，本文沿边坡水平方向设置了5个测量圆，监测其内部应力的变化过程，同时在测量圆中部设置位移监测点，监测路基高边坡的运动过程。

5 计算结果分析

5.1 路基高边坡破坏特征

不同时步下路基高边坡位移大小及边坡形态见图3。图3(a)为边坡启滑状态，该时刻不同位置监测点位移情况如图4所示。开始滑坡阶段边坡中部位移最大，达到0.83 m；坡顶位移最小，趋于0。对于小河段边坡，中部土质的不稳定是诱导边坡滑动的主因。分析其原因主要有：①由于边坡坡度稍陡且中部土体较厚，中部土体在自重作用下下滑力最大。②在平衡状态下，边坡中部土体受下部土体的支挡作用，同时受上部土体的牵引作用，上部土体和下部土体共同作用下，保持着中部土体的平衡。在降雨作用下，上部和下部边坡土体强度严重弱化，失去对中部土体的牵引作用，导致中部土体首先启滑。

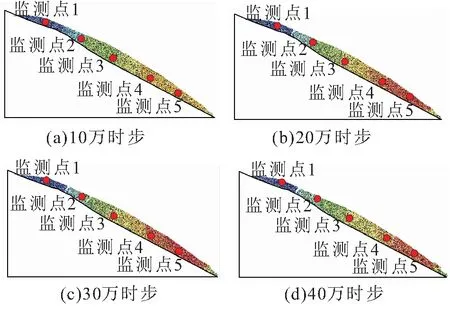
图3 不同时步下路基高边坡位移及滑移形态

图4 启滑阶段不同监测点位移 图5 不同监测点位移曲线

计算达到20万时步时，见图3(b)，由于中部边坡滑动位移较大，上部边坡出现拉裂隙，边坡上部处于低速滑动状态。其中边坡下部位移开始增大，但仍保持较低水平，对边坡中部土体有一定支撑作用。计算到30万时步时，见图3(c)，边坡整体滑动较大，中部开始产生裂纹，由于上部边坡对下部的推动作用，下部边坡土体位移明显增大，呈加速状态，裂纹继而向边坡下部传递。当计算达到40万时步时，见图3(d)，边坡沿坡脚位置剪出破坏，边坡上部土体由于坡率小，处于自稳状态，中部土体在下部支撑作用下，匀速下滑，下部土体发生剪出破坏，路基高边坡完全失稳。

在降雨作用下，上部和下部边坡土体强度进一步弱化，上部土体牵引作用降低，最先形成宏观拉裂纹，在土体强度降低及上部土体挤压作用下，下部土体逐渐从坡底剪出，边坡失稳，发生大规模滑动。

5.2 路基高边坡运动特征

沿边坡高度方向在坡表设置5处位移及速度监测点，监测滑坡全过程的位移及速度变化特征，见图5及图6。在启滑阶段，边坡中部速度较大，达到了0.25 m/s，远远高于边坡其他位置，边坡从中部开始滑动。当计算了30万时步时，边坡中部速度明显降低，保持在0.08 m/s；下部土体速度最大，达到了0.23 m/s。在滑坡全过程中，下部土体总位移最大，达到了2.83 m，中部土体位移其次，达到了1.35 m；边坡上部土体受拉破坏，与中下部土体分离，处于自稳状态，位移和速度均趋向于0。

图6 不同监测点速度曲线

滑坡最本质的原因是应力变化，图7为不同监测点位置的应力变化特性。在滑坡的瞬间，边坡中部土体应力明显降低，下部基岩对其粘结作用明显减弱。监测点1处于自稳状态，土体应力在滑坡全过程中，保持在22.5 kPa，与前分析相符。可以发现：在应力方面，路基高边坡下部受上部土体推挤作用，其应力水平始终保持较高水平，最大达到了82.7 kPa；在滑移速度方面，边坡下部土体对上部土体有明显的支撑作用，降低了上部土体滑动速度；而上部土体对下部土体推挤作用，使下部土体位移明显增大。

图7 不同监测点应力曲线

高边坡滑动过程中应力呈现差异性变化，下部坡脚呈支挡作用，一定程度上减小上部边坡滑动速度，最终降低后期大范围滑坡风险。工程边坡需重点控制住中部及上部土体启滑。

6 结论

(1)基于颗粒离散元中的接触粘结模型，建立双轴标定试验，通过大量重复数值试验，确定了土体的破坏主应力线，得到细观参数与小河段边坡土体宏观参数对应关系。

(2)小河段土质高边坡启滑开始于边坡中部，随着降雨作用的延长，在土体强度弱化及重力增加的双重作用下，边坡上部土体牵引作用降低，界面处出现宏观裂缝，边坡下部土体在中部土体挤压作用下内部土压力增大。

(3)高边坡滑动过程呈现逐级差异破坏，边坡以上部土体出现拉裂开始，而后下部土体从坡脚剪出，最后中间土体不断出现拉裂纹，呈块体形态。