偏心受压圆柱形气囊结构静态力学特性研究

吕 霖， 樊自建， 孙海涛

(国防科技大学空天科学学院，湖南 长沙 410073)

气囊具有重量轻、收纳体积小、充气后承载能力大等优点，在航空航天、船舶工程、建筑工程等领域被广泛采用。由于囊体属于柔性结构，受力后变形较大，因此囊体的工程应用案例大都可以简化为刚性面板与气囊相结合的板囊组合结构；在这一结构中，囊体在刚性面板挤压作用下的变形特性直接关系到板囊组合结构的承载性能和使用安全。刚性面板的挤压载荷与囊体变形之间的关系表现为复杂的非线性关系，且受到囊体结构外形、尺寸及囊体初始超压等多种因素的影响。从现有文献看，有关板囊组合结构中囊体受压变形的研究主要集中在刚性面板受均布下压载荷作用时囊体压缩变形、内部超压与外部载荷关系方面的研究。文献[1]通过试验和数值仿真研究了刚性面板均匀下压作用下气囊承压、变形和内部超压变化的关系；文献[2-3]通过静力分析简化气囊为线性弹簧模型得出气囊受力变形与刚性面板上中心载荷作用关系的近似公式；文献[4-6]通过有限元仿真计算研究了刚性面板受中心载荷作用时，囊体尺寸、内部超压等因素对气囊变形特性的影响。

但是，工程应用中的板囊组合结构常由于载荷的偏心作用或囊体支撑平面倾斜等因素的影响出现偏心受压的工况[7]，而有关气囊在刚性面板受偏心载荷作用时囊体的静态力学特性未见相关研究报道。本文在已有刚性面板均匀下压作用下囊体变形特性研究成果基础上，通过对板囊组合结构中囊体结构变形过程中几何变形与相互作用力的合理简化，建立了适用于均匀下压变形和横向倾斜下压变形情况下囊体变形、内压及刚性面板承载力关系的数学模型，并进一步对比分析了不同变形状态下气囊静态承载性能与内压的关系。

1 数学模型建立与验证分析

1.1 囊体受力变形过程分析简化与几何描述

板囊组合结构如图1所示。当外力作用在刚性面板上时，刚性面板将外部集中力的作用均匀分散到与囊体的接触表面，囊体在上部刚性面板的下压和下部刚性地面的约束作用下发生瘪化变形，使得上下接触面面积增大，从而可提供更大的支撑力与上面板外部荷载作用相平衡。如果外部作用力的合力作用点在刚性面板的中心，则囊体发生均匀下压变形；如果合力作用点偏离刚性面板的中心，则板囊组合结构将会发生倾斜变形。为了建立囊体变形与外力作用的关系，需对这一作用过程做如下简化假设：

图1 板囊组合结构

(1)认为各变形工况下，囊体与上部面板、下部地面紧密贴合，呈面面接触。非接触处囊体外形始终与上下接触面相切且呈半圆弧状；由于气囊两端锥体段所占囊体总体积比例很小，因此忽略锥体段的影响，认为仅囊体圆柱段提供有效支撑。

(2)忽略承压变形过程中，囊体材料周向、轴向与厚度方向的变形，即认为承压变形前后囊体表面积不变[4]。

(3)忽略因囊体表面变形不协调而产生的褶皱现象对囊体承载能力的影响，忽略气囊端部封头对气囊承载力的影响。

(4)认为气囊承压变形过程为准静态过程，囊体内气体温度无变化，且在各变形工况下均保持受力平衡。

1.2 建立囊体受力变形过程数学模型

基于以上假设，认为气囊在初始超压P1作用下充分张紧，呈直径为D、母线长为L、厚度为t的薄壁圆柱形结构。当上部面板承受沿纵向对称轴y轴偏离中心一定位置的载荷FG作用，面板中心产生的位移为w，并导致面板产生横倾，横倾角度为θ，气囊在面板偏心荷载作用下发生的变形如图2所示。此时，气囊变形以yoz平面为对称面，内部超压为P2；气囊所能提供的支撑力为FR，方向垂直于作用面；所能提供的竖向承载力为FC，此力与刚性面板上的载荷FG作用相平衡。

图2 气囊承压变形

将气囊沿母线方向分为n段，每段长δ=L/n，设从上面板最低端部起第i段受压气囊的工作高度为Hi(i≤n)，接触段长度为Bi。则气囊承压变形后第i段气囊参数满足：

2Ri=Hi=H0+iδtanθ

(1)

Bi=π(D-Hi)/2

(2)

di=D-Hi

(3)

式中：H0为气囊最低工作高度；Ri为囊体非接触处圆弧半径；di为第i段气囊位移压缩量。

气囊初始体积V1与承压变形后体积V2分别为：

V1=πD2L/4

(4)

(5)

气囊与刚性面板的接触面积S：

(6)

视气囊为封闭容器，当环境气压为P0时，由于承压变形过程中忽略了囊体内气体温度变化的影响，故可认为其满足理想气体状态方程[8]:

(P0+P1)V1=(P0+P2)V2

(7)

根据基本力学关系，可得接触面支撑力FR、承载力FC及其作用点坐标(0,y)满足如下关系：

FR=P2S

(8)

FC=FG=FRcosθ

(9)

(10)

至此根据以上假设分析，本文建立了适用于各种变形工况下气囊变形与承载力、内压关系数学模型。通过式(1)～式(10)，在已知气囊直径、长度、初始内压和变形状态时，即可计算气囊内压的变化以及气囊的承载力和外部载荷的偏心距。

1.3 数学模型试验验证与分析

文献[1]对某直径D=0.8 m的气囊，在初始超压P1=50 kPa下，竖直变形过程中气囊承载力FC、内压P2和上部面板中心位移量w之间的关系开展了试验研究。表1给出了试验测得的数据。

表1 试验结果[1]

由上述受囊体受力分析模型可知，当气囊处于均匀竖直下压变形工况时，即θ=0°，每段气囊的竖向压缩量di等于上部面板中心位移量w，即满足di=di+1=w，B=πw/2。对于表面积为SA=πDL的气囊，通过基本力学关系式(8)、式(9)，理想气体状态方程式(7),以及相关变形几何公式(1)～式(6)，可推得承载力FC与面板中心位移w满足如下关系式：

(11)

图3给出了囊体竖直均匀变形下气囊承载力变化曲线的理论计算值和试验值。从图中可以看出，试验数据与本文数学模型计算结果基本吻合，数学模型较好地反映了承载力随囊体竖向均匀压缩位移增加呈非线性增长的趋势。

图3 囊体竖直变形与承载力、气囊内压关系

此外从式(11)还可看出竖直变形时，对于表面积SA相同的气囊，在相同初始超压P1下其所能提供承载力FC的大小只与压缩比w/D有关。在相同的压缩比w/D下，承载力FC会随着初始超压P1的增长呈线性增长。从生产制作经济性角度考虑，由此说明，相同表面积SA下，长径比L/D越大、初始超压P1越高的气囊具有越高的刚度。

依据上述数学模型，通过整理还可得出气囊内压P2与上面板均匀下移位移w的关系式如下：

(12)

图3给出了囊体竖直均匀变形下气囊内压变化曲线的理论计算值和试验值。从图中可以看出，当囊体压力较低时两者吻合较好；当上部面板中心位移量大于50%D囊体内压快速增长时，数学模型计算结果明显小于试验数据，且随着压力的升高两者之间的差距逐渐增大。分析建模假设可知，这主要是由于数学模型忽略了气囊大变形下必然发生的囊壁褶皱以及囊体内气体温度升高等影响因素，而最终导致了误差的产生。

此外，从式(12)可以看出竖直均匀变形时，气囊在相同初始超压P1下，其内压P2只与压缩比w/D有关，且随着上部面板中心位移量w的增大呈非线性的增长。在相同的压缩比w/D下，内压P2会随着初始超压P1的增长呈线性增长。

综上所述，本文建立的数学模型计算数据与试验结果一致性较好，可以较为准确描述囊体在压缩变形过程中囊体结构尺寸、初始压力与囊体承载性能之间的关系。

2 刚性面板偏心受压下囊体变形与承载性能分析

当上部刚性面板所受载荷沿轴向偏离面板中心一定距离时，载荷偏心作用一侧囊体受力变形增大，上部面板向该侧倾斜，气囊呈一端高，一端低的倾斜变形状态。为讨论不同横倾变形工况下气囊静态力学特性变化，将偏心受压过程分为两步：第一步为载荷中心正压作用下的竖直变形，第二步为力矩作用下绕某旋转中心产生的横倾变形，认为旋转中心保持第一步竖直变形高度不同。

鉴于对气囊进行横倾变形测量有一定的难度，难以获得试验实测数据。为研究不同承压变形时气囊力学特性的差异，以某母线长度L为2.8 m、直径D为0.8 m型号气囊为计算对象[9]，通过研究不同变形工况下气囊承载力与内压的变化关系，为板囊组合结构载荷通行提供参考指导。且由于不同旋转中心均可通过简单的换算使其与某变形工况下上部面板中心重合，为便于讨论，下文均以上部面板中心作为旋转中心。

2.1 囊体倾斜变形与气囊内压变化关系

依据本文建立的模型分析计算了刚性面板中心位移、横倾偏斜角度、初始压力与囊体内压变化百分比之间的关系，如图4所示。

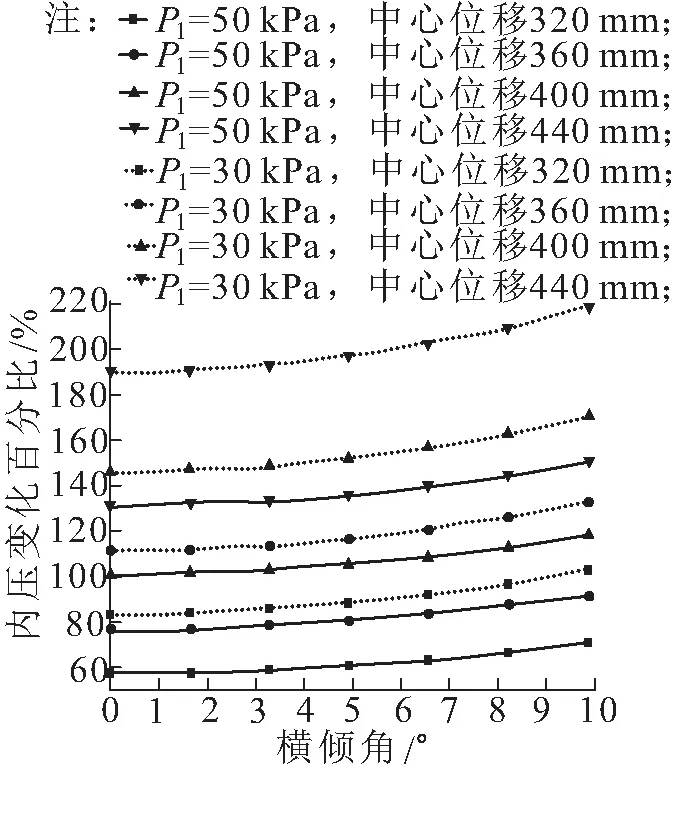
图4 气囊内压变化百分比与横倾角关系

从图中可以看出在刚性面板中心竖向位移一定时，囊体的内压随面板横向倾斜角度的增加呈非线性增长。同一倾斜角度、同一初始内压下，囊体内压变化百分比与面板中心竖向位移亦呈非线性增长关系；在中心竖向位移一定的情况下，倾角与内压的变化百分比的非线性变化趋势不受初始内压变化的影响；同一竖向位移、同一倾斜角度下，高初始内压的内压变化百分比要远低于低内压的内压变化百分比。

2.2 囊体变形与承载力变化关系

图5为不同变形工况下，囊体变形与承载力变化关系。从图中可以看出,当面板中心位移一定时，随着面板倾角的增大，囊体的承载能力缓慢非线性增大；对比图中不同初始压力、相同中心竖向位移的倾角变化关系，可以看出此变化关系不受初始压力变化的影响。

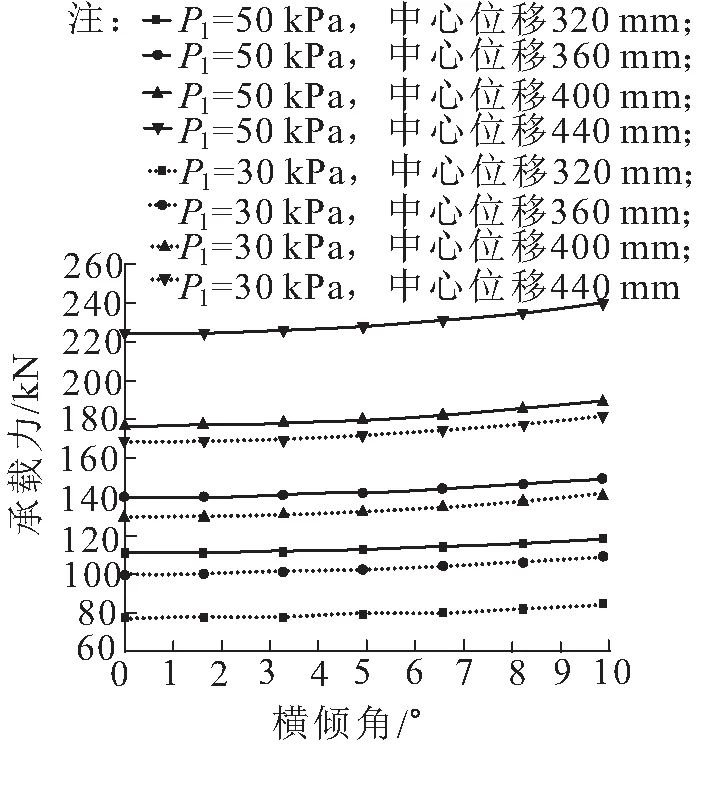
图5 承载力大小与横倾角关系

以承载力作用点偏离面板中心的y向距离作为偏心距，由数学模型易知偏心距只与气囊变形情况有关，即相同变形条件下，初始内压的大小只影响承载力的大小，而不会改变其作用点位置。

图6为不同中心竖向位移条件下，承载力的偏心距与囊体倾斜变形角度之间的关系。从图中可以看出，在相同中心位移下，随着横倾角度的增加偏心距呈线性增长，且随着中心位移的增加其增长速率会逐渐减缓。在相同横倾角度下，偏心距随着中心位移的增加呈非线性减小，且随着横倾角度的增大该非线性会愈加显著。

图6 偏心距与横倾角关系(P1=50 kPa)

3 结论

(1)本文建立的囊体静力特性分析模型与试验测量结果具有较好的一致性，可用于刚性面板中心载荷作用和偏心荷载作用下囊体静力特性的分析。

(2)在竖向均匀压缩下，气囊在相同初始超压P1作用下，其内压P2只与压缩比w/D有关，且随着上部面板中心位移量w的增大呈非线性的增长。

(3)在偏心受压下，相同中心位移时囊体内压P2与承载力FC随横倾角增大呈非线性增长的趋势不受囊体初始超压P1的影响。

(4)在偏心受压下，相同中心位移时随着横倾角度的增加偏心距呈线性增长，且随着中心位移的增加其增长速率会逐渐减缓。对于相同横倾角度，偏心距随着中心位移的增加呈非线性减小，且随着横倾角度的增大该非线性会愈加显著。