爆炸载荷下薄板异常动力响应模式及载荷特征影响研究*

邱梓恒 翟红波 刘文洋† 毛伯永 侯淑娟

(1.湖南大学 机械与运载工程学院，长沙 410000)(2. 西安近代化学研究所，西安 710065)

引言

薄板在爆炸冲击载荷作用下的变形预测通常只关注爆炸冲击载荷的正相冲击压力(后简称正压)，而忽略负相压力(后简称负压).这在爆炸点距离薄板较近或者当量较大的情况下是合理的，此时薄板的变形失效过程受爆炸冲击正压主导[1, 2].由于爆炸冲击的正压极值远大于负压极值，薄板变形方向与冲击波方向一致.但是，当爆炸点距离薄板较远或者当量较小的情况下，忽略爆炸冲击负压则不合理.在反射超压峰值与负压峰值大小相近时，负压对结构动力响应影响不可忽略[3].V. Aune等人发现爆炸冲击载荷的负压阶段会改变薄板最终构型[4].余同希、李庆明等人发现爆炸冲击载荷下的薄板弹塑性动力响应可分成两类[5-8].若中心的永久偏转方向与冲击波方向相同，则称之为直观变形模式；若中心的永久偏转方向与冲击波方向相反，则称之为异常(反直观)变形模式.

薄板异常动力响应受载荷、边界条件、材料、几何形状的影响[9, 10].大多数薄板异常动力响应的研究采用简化载荷如矩形或三角形脉冲，与真实爆炸冲击载荷相差较大；若采用商业软件中内嵌的爆炸冲击经验模型，则难以分离载荷特征变量，从而无法分析其对异常动力响应的影响.本文使用经实验数据验证的自主开发载荷模型，从爆炸载荷冲击波的特征入手，分析了影响方形薄板动力行为的因素；通过控制距离当量比，发现了方形薄板变形模式的变化规律，并进一步分析了薄板异常动力行为与塑性耗散能之间的关系.

1 爆炸冲击载荷压强-时间历程

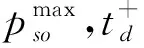
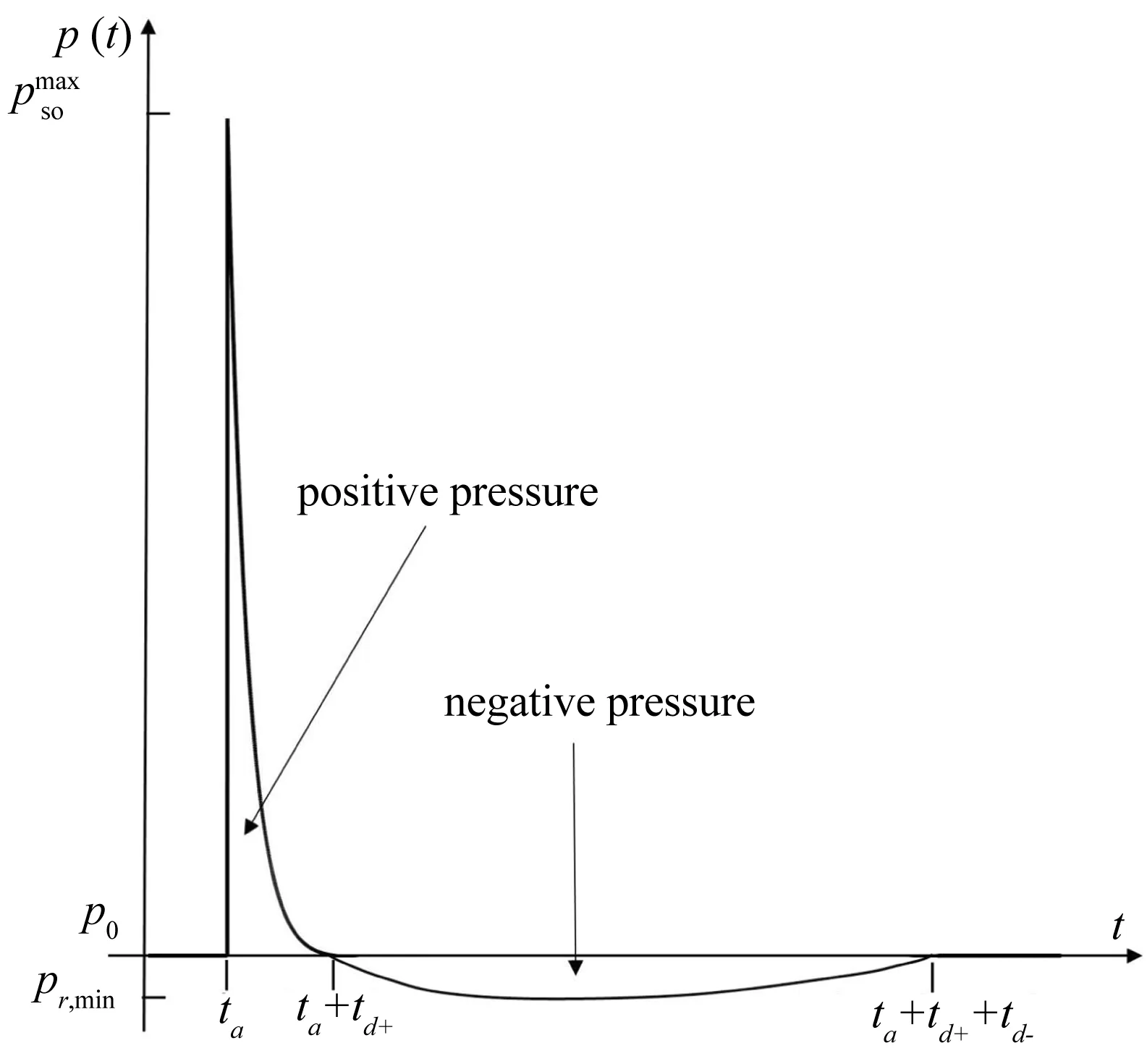
图1 爆炸冲击载荷压强随时间变化示意图Fig.1 Typical pressure-time history for a blast wave

Kinney和Graham将大量球形、半球形冲击实验的冲击波压强数据通过距离当量比(Z=R/W1/3) 和等效TNT质量(W)作为自变量组成的高阶多项式对载荷特征参数进行曲线拟合[11].

1.1 冲击波正压

正压压强-时间历程可由修正的Friedlander[12]方程描述，即

p(t)=

(1)

其中，当冲击波遇到与其方向不平行的结构时发生斜反射，冲击压力增强，形成斜反射压力prα.

(2)

方程：

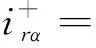
(3)

将正相冲量拟合公式代入式(3)可迭代求解衰减系数b.衰减系数b是关于爆炸距离R与等效TNT质量W的函数.该值在一定的R/W区域内呈现高度非线性.图2 直观描述了衰减系数b随爆炸距离R与等效TNT质量W的变化.可以发现当爆炸距离R恒定时，等效TNT质量在10g以上衰减系数b的变化较为平缓；而等效TNT质量在0g-10g之间，衰减系数b随等效TNT质量减小急剧增大，并且在等效TNT质量接近0时又快速减小，在该区间内呈现出“∧”型.而在等效TNT质量恒定的情况下，衰减系数b随爆炸距离R的变化相对平稳.这表明爆炸距离与等效TNT质量对衰减系数b的影响程度不同，等效TNT质量对衰减系数b的影响更加显著.

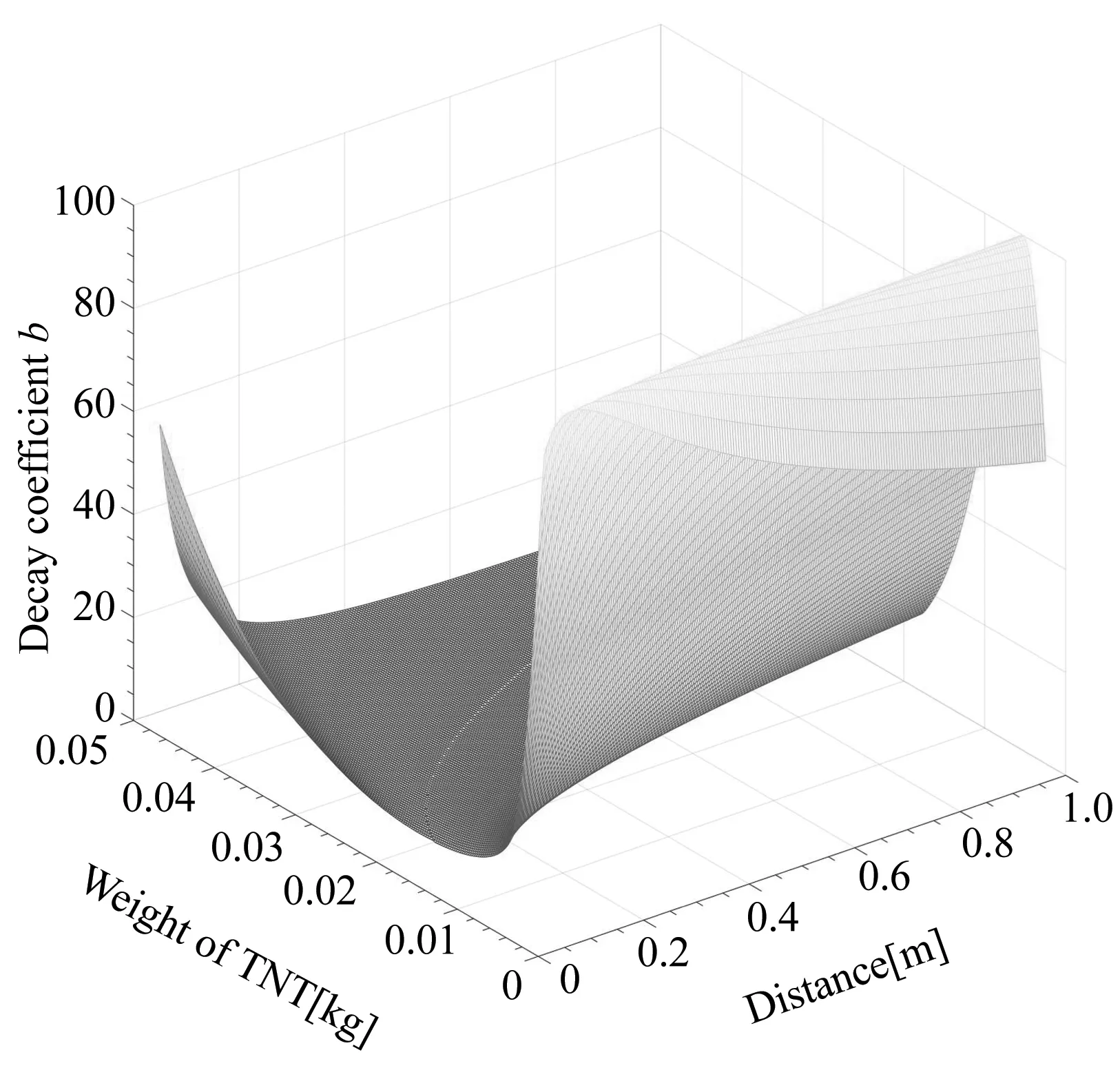
图2 衰减系数b变化趋势Fig.2 Variation trend of decay coefficient b

1.2 冲击波负压

关于爆炸冲击载荷的负压，其描述方式有两种[15]：(1) 双线性描述法；(2) 三次曲线描述法.对于双线性描述法，爆炸冲击载荷的负压被分成两部分，压强随时间线性变化.双线性描述法压强随时间的分段函数如下.其中α为负压时间比例参数，控制负压压强上升时间在整个负压持续时间的占比.

(4)

三次曲线描述法则采用一条三次曲线拟合爆炸冲击载荷的负压变化过程.其中负压上升时间大致占负压持续时长的三分之一．

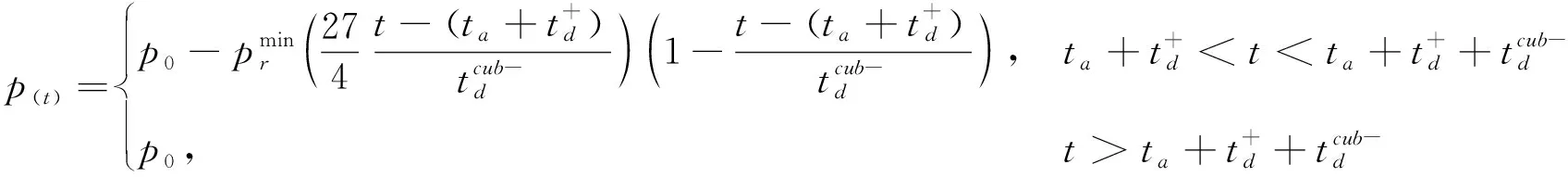
(5)

(6)

(7)

(8)

(9)

2 仿真试验模型

爆炸冲击载荷下薄板异常动力响应对外界条件较为敏感.其中不仅爆炸载荷等效TNT质量W、爆炸距离R以及爆炸冲击载荷模型的各项参数对薄板异常动力响应的仿真结果有着显著影响，薄板的几何形状、材料属性、边界约束条件等因素对仿真结果也会造成较大的影响.为模拟试验工况，建立了较为复杂的几何模型.材料本构为修正Johnson-Cook模型.使用ABAQUS 用户子程序实现了自主开发爆炸冲击载荷的加载以及材料本构的赋予.

2.1 几何模型

金属薄板两侧用钢制夹具夹持并以螺栓固定.金属薄板尺寸为400mm×400mm×0.8mm，两侧钢制夹具宽度为50mm，螺栓直径为20mm，金属薄板的实际受载区域为300mm×300mm.爆炸载荷加载在金属薄板正中心，整体结构中心对称，为增加计算效率，采用四分之一建模法.钢制夹具外围施加固支约束.其中薄板为三维连续壳单元(S4R)；钢制夹具与圆柱螺栓均为三维实体单元(C3D8R),如图3所示.金属薄板采用1050A-H14铝材，材料属性如表1.钢制夹具材料属性如表2.

图3 几何模型Fig.3 Geometric model

表1 1050A-H14铝材料属性Table 1 Material properties of 1050A-H14 aluminum

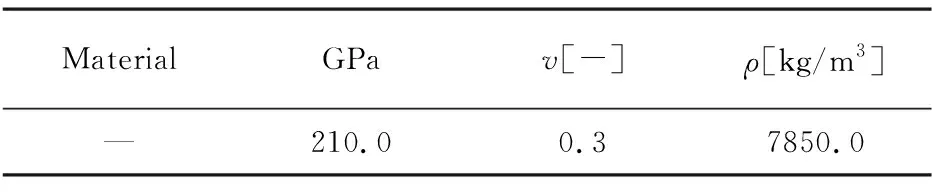
表2 钢材料属性Table 2 Material properties of steel

为模拟实际工况中螺栓螺帽与螺母为薄板两侧的钢制夹具提供预紧力，在模型两侧的钢制夹具外表面螺栓周围一圈施加均布压力500MPa，螺栓上下表面与夹具绑定约束.为模拟金属薄板与夹具接触面之间滑动摩擦力，设置有切向行为表面接触，静摩擦系数为0.15，动摩擦系数为0.1.爆炸载荷等效TNT质量为41.2g，距离铝板中心625mm，四周无反射面.

2.2 材料本构

为模拟材料弹塑性大变形，将变形率加法分解为弹性和塑性两部分

D=De+Dp

(10)

式中，De为弹性变形率，Dp为塑性变形率.弹性变形率与柯西应力之间的本构关系为

(11)

式中，E为杨氏模量，ν为泊松比，σ∇J为柯西应力的Jaumann率，I为单位张量.对于各向同性材料，屈服函数采用

f(σ,εp,T)=σeq-σy(εp,T)

(12)

式中，σeq为等效应力，εp为等效塑性应变，T为温度．

(13)

(14)

式中，σ′为应力偏量，应变增量与应力偏量有关.材料屈服应力函数采用修正Johnson-Cook模型[17]

σy=

(15)

(16)

式中，Tr为环境温度，Tm为材料熔点.假设塑性势函数与屈服函数重合，塑性变形率可通过相关联流动法则表达为

(17)

金属材料在爆炸载荷下迅速发生剧烈塑性变形产生温升，可假设为绝热过程.温升速率的表达式为

(18)

式中，χ为Taylor-Quinney系数，ρ为密度，Cp为比热.

3 仿真验证与结果讨论

3.1 仿真验证

爆炸冲击载荷各项特征参数对薄板反直观异常动力响应有着诸多影响.本文采用经实验数据验证的自主开发爆炸冲击载荷模型对薄板反直观异常动力响应进行模拟研究.在研究过程中发现爆炸载荷负压采用三次曲线描述法时薄板中心挠度到达负方向最大值时间早于双线性描述法，与实验结果差异较大.因此后续仿真结果除特别说明外爆炸载荷负压均采用双线性描述法.图4对比了实验与仿真的结果.其中两次实验的外界条件一致，但薄板反直观行为的敏感性导致结果略有差异.图4(a)中仿真预测的薄板正向变形历程与实验整体一致，回弹曲线位于两次实验曲线中间，薄板达到正方向最大值的时间点完全一致，达到负方向最大值的时间点吻合，但仿真回弹最大挠度略高于实验结果，这可能是由于负压冲量估值略大于实际值.图4(b)中薄板负方向挠度最大值仿真与实验基本一致.通过对比仿真与试验的薄板变形历程与最终构型，验证了爆炸冲击载荷模型的准确性.

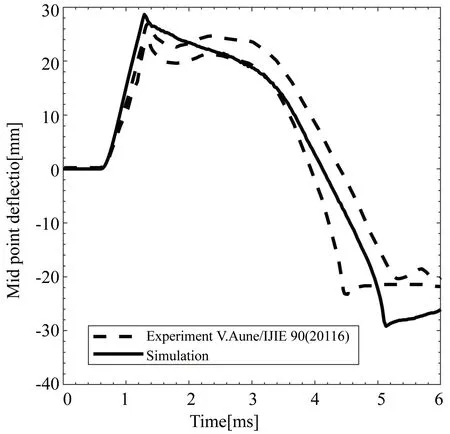
(a) 薄板中心挠度随时间变化历程 (a) Variation history of central deflection

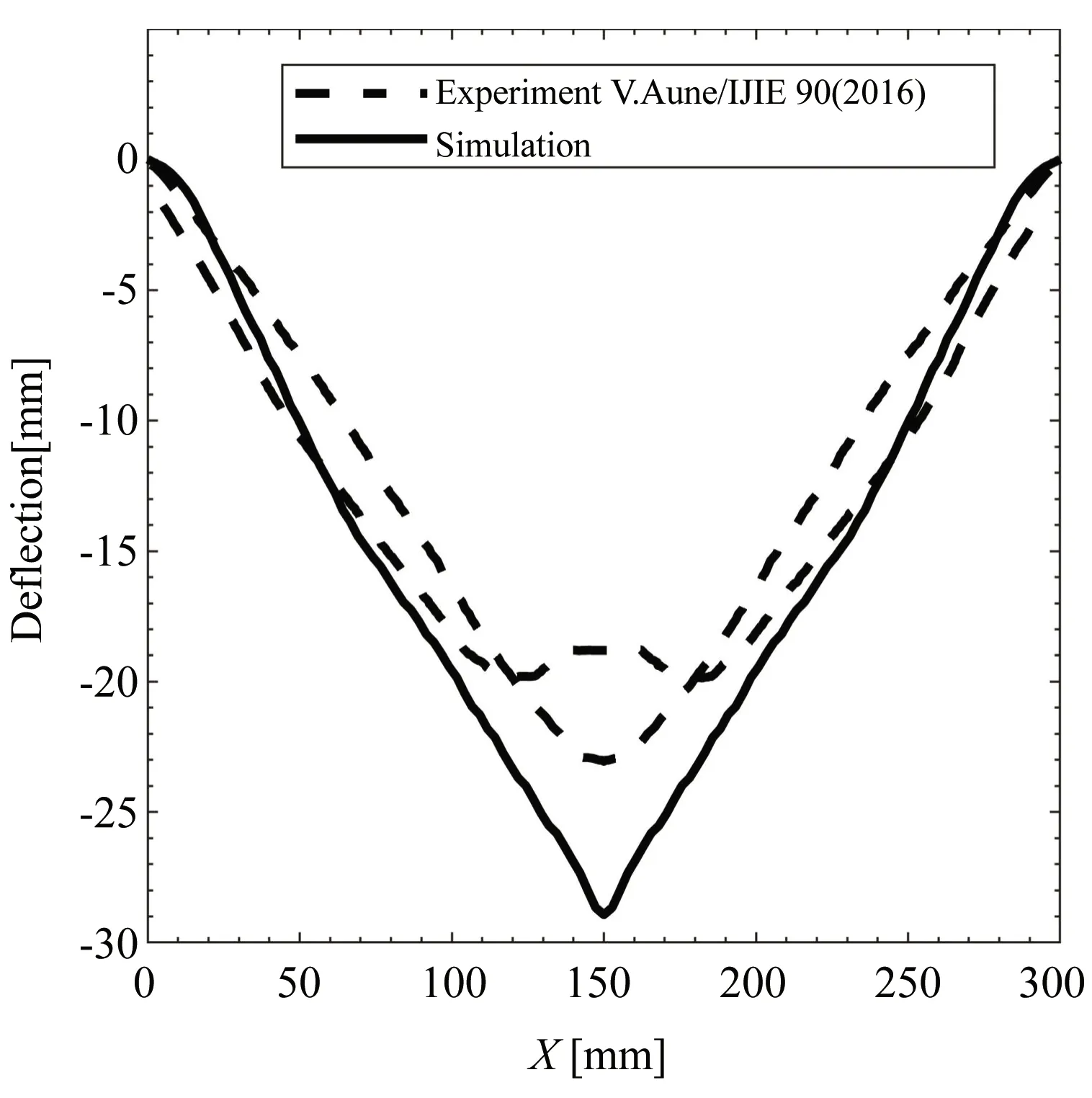
(b) 薄板中线最终构型 (b) Final configuration of thin plate centerline 图4 实验与仿真结果对比Fig.4 Comparison of experimental and simulation

薄板在爆炸冲击载荷下的变形过程具有“先边缘，后中心”的特性.图5为等时间间隔薄板变形过程.在1 ms时波阵面刚抵达，薄板边缘部分先发生变形，而中间部分仍保持平直，表明薄板的变形是由边缘部分向中心部分逐渐扩散的.在3 ms时薄板中心外围区域先回弹至负方向，中心位置最晚到达负方向极值.表明回弹过程变形也是从板边缘向中心逐渐发展.

图5 薄板等时间间隔变形图Fig.5 Equal time interval deformation diagram of thin plate

3.2 负压对薄板动力响应的影响

由于负压压强极值远低于正压压强极值，研究结构受爆炸冲击载荷的动力行为时，冲击波负压常常被忽略.这种简化适用于板厚较厚、刚度较强情况下的动力响应仿真，但对于较为敏感的薄板结构，负压会对仿真结果产生不可忽视的影响.图6(a)、(b)分别为薄板在有无负压情况下中心挠度变化历程的仿真结果.在1.2 ms之前，由于爆炸冲击波处于正压阶段，两次仿真的结果完全一致.在1.2 ms后，有负压作用下的薄板开始回弹，并发生了反直观异常动力响应；没有加载负压的薄板则发生直观行为.结果表明爆炸冲击负压对薄板异常动力响应的发生至关重要.因此，下文对爆炸冲击载荷负压的影响进行分析.

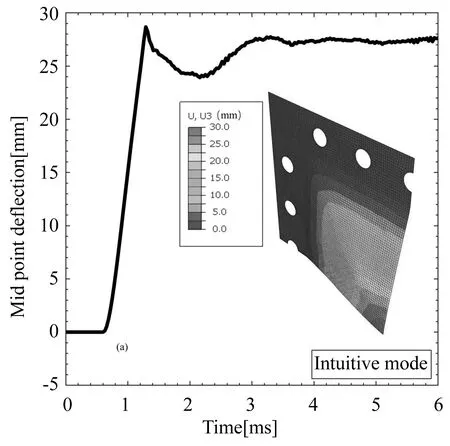
(a) 不考虑负压的薄板中心挠度变化历程(a) Variation history of central deflection without negative pressure

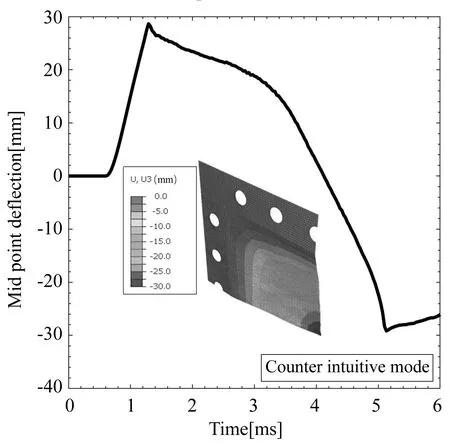
(b) 考虑负压的薄板中心挠度变化历程(b) Variation history of central deflection with negative pressure图6 负压对薄板动力行为的影响Fig.6 Influence of negative pressure on dynamic behavior

3.2.1 负压描述法的影响

爆炸载荷负压段使得准确预测薄板反直观行为结果更加复杂.图7(a)对比了在同一工况下分别采用双线性与三次曲线两种负压描述方式的薄板中心挠度变化历程.结果表明，三次曲线加载下薄板回弹速度更快，中心挠度先于双线性负压加载到达负方向极值.造成双线性负压加载下薄板回弹时间延长的原因与负压持续时间有关，当负压冲量和负压极值一致时，双线性加载方式负压持续时间略长于三次曲线加载，两者相差12.5%.爆炸过程的高度非线性放大了两者的差异，两种加载方式薄板中心挠度到达负方向极值时间相差22.2%.在双线性、三次曲线两种不同负压加载模式下薄板反直观行为最终挠度值基本相等，这是由于爆炸载荷负压冲量相等.

(a) 三次曲线加载与双线性加载仿真结果对比(a) Comparison of simulation results between cubic and bilinear profile

(b) 双线性加载参数α=0.4与0.8仿真结果对比(b) Simulation results of parameters α=0.4 and 0.8图7 负压描述法对薄板中心挠度变化历程影响Fig.7 Influence of negative pressure profile on variation history of central deflection of thin plate

使用双线性负压加载方式时，描述负压过程中到达负压极值所需时间在整个负压时间段所占比例的参数α对薄板反直观行为的数值模拟结果有着较大的影响.图7(b)对比了参数α=0.4与α=0.8两种情况下薄板中心挠度变化历程.当参数α=0.8时，薄板中心挠度达到负方向极值的时间晚于参数α=0.4，而薄板中心挠度负方向极值两次模拟结果一致.在冲击波负压段冲量一定的情况下，薄板中心挠度极值基本不变.负压压强随时间历程的改变引起薄板中心挠度时间历程的变化.

图8进一步表明了不同的负压时间比例参数α下，薄板中心挠度负方向极值和薄板中心挠度负方向极值到达时间的变化趋势.薄板中心挠度最高最低值之差仅有2.14 mm，不超过平均值的7%，由此可知，参数α的变化几乎不会影响薄板回弹至负方向的极值.但是，参数α对薄板回弹时间历程有着显著影响.随着负压极值到达时间的延后，薄板中心挠度到达最低值的时间也在延后，其最高最低值之差达到平均值的21%.

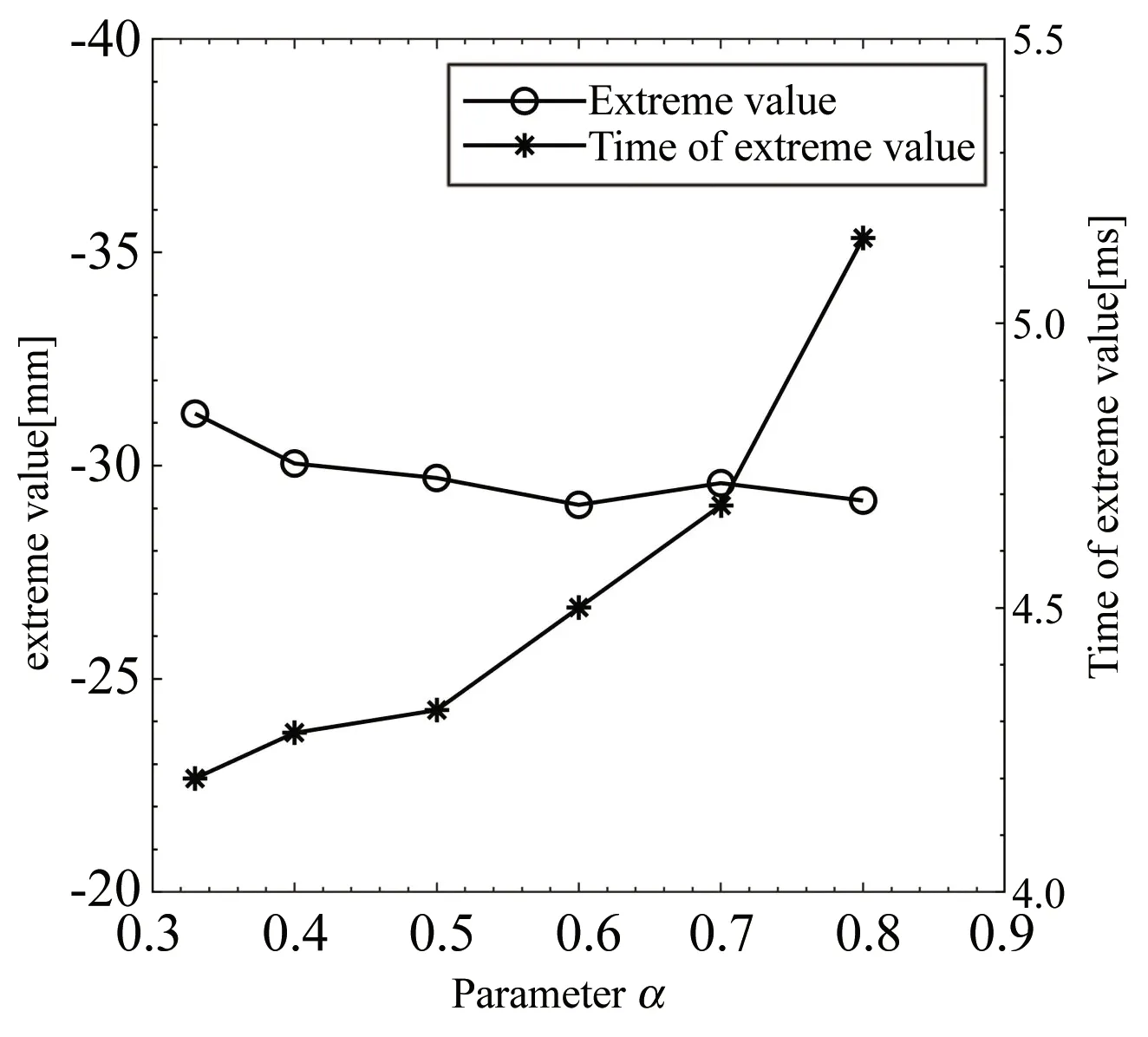
图8 负压时间比例参数α的影响Fig.8 Influence of negative pressure time parameter α

综上，爆炸载荷负压段描述方式仅对薄板变形回弹时间历程产生影响,对负方向挠度极值没有影响.

3.2.2 正压冲量与衰减系数b

不同学者提出了多种冲击波正压冲量计算公式.衰减系数b受正压冲量控制，并且两者呈非线性关系.选取了两种基于试验数据的正压冲量拟合公式[13, 15]分别进行仿真实验.图9对比了两种正压冲量计算方法薄板中心挠度时间历程的结果.

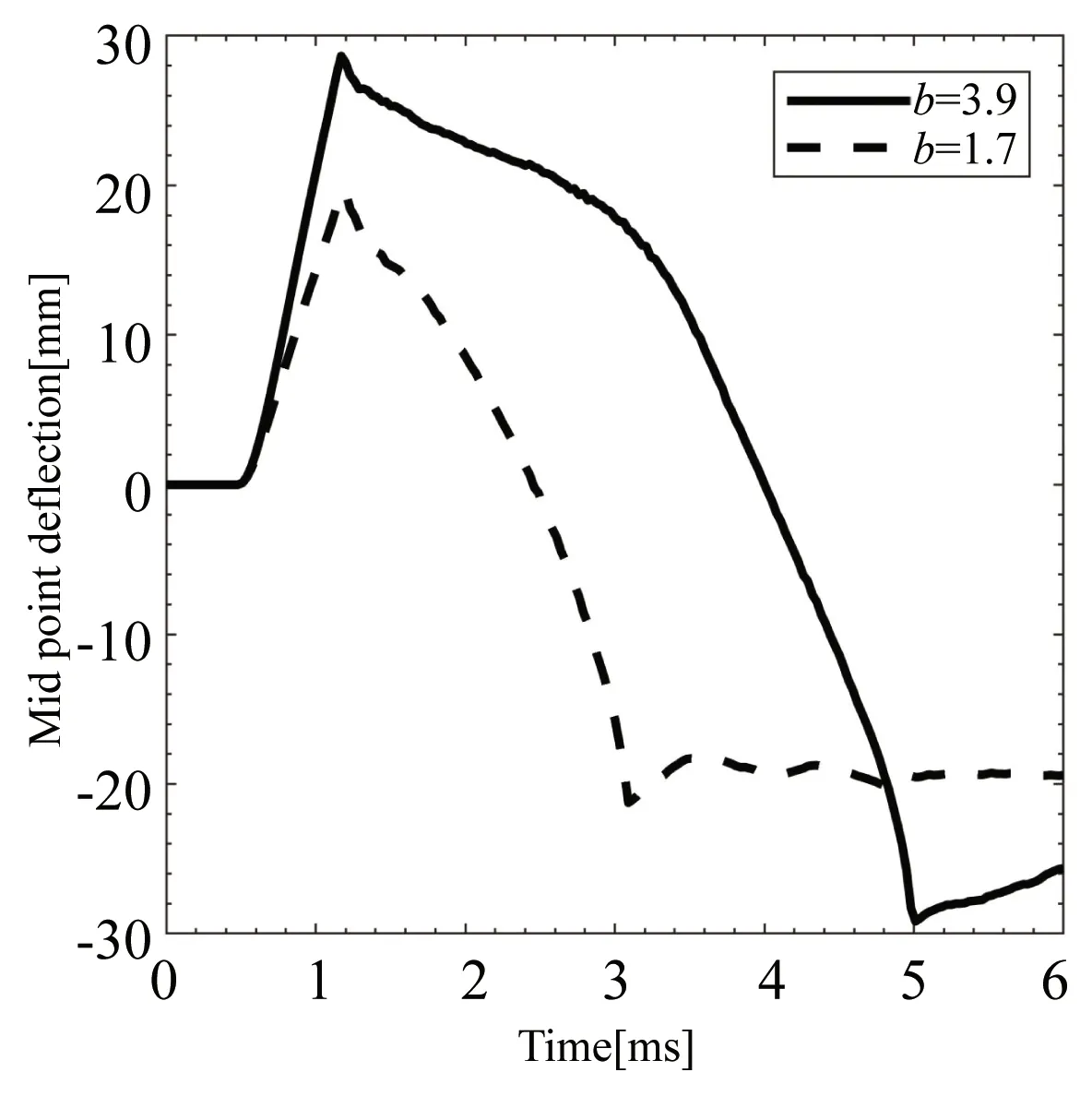
图9 衰减系数对薄板动力响应的影响Fig.9 Influence of decay coefficient on dynamic response of thin plate

两者正压冲量相差36%，薄板中心挠度正方向极值差10 mm，均在1.2 ms达到正方向极值.在1.2 ms后两者开始回弹过程，到达负方向极值时间相差2 ms，薄板中心挠度负方向极值差8 mm.由此可以发现，在薄板向正方向变形的过程中，变形持续时间并未受到正压冲量及衰减系数变化的影响，而这两者的变化引起了薄板挠度正负方向极值与回弹时间历程的不同.

4 薄板动力响应与模式转变

大多数研究采用距离当量比Z衡量冲击强度并通过调整Z值来研究结构在不同爆炸冲击强度下的动力行为.但是，薄板在爆炸冲击载荷下的动力行为复杂，其行为模式不单一取决于正负压极值.仅通过调整距离当量比Z难以探明薄板动力行为与爆炸冲击载荷的关系.因此，需要进一步讨论薄板动力行为与其他冲击波控制量的关系.

4.1 薄板动力响应模式

保持距离当量比Z不变，则冲击波正负压极值即冲击强度恒定.通过改变爆炸距离R，可以实现在冲击波强度不变的情况下改变冲击波正负压持

续时间，冲击波冲量也随之变化.在此条件下，冲击波冲量与爆炸距离R呈正相关.

取Z=1.809m/kg1/3,R由375mm逐渐递增至750mm，不同爆炸距离薄板变形模式总结如表3所示.在冲击强度不变的情况下，薄板动力行为仍可以表现出四种模式：模式一、继发直观模式；模式二、反直观模式；模式三、始发直观模式；模式四、混合模式.其中，继发直观模式表现为薄板到达初次变形极值后向负方向发生反向屈曲，在到达负向极值后向正方向再次发生反向屈曲并最终停留在正方向一侧，如图10 (a)所示.而始发直观模式下，薄板在初次正向变形后不会发生反向屈曲，直接停留在正方向一侧.图10(b)为继发直观模式薄板最终构型.通过与图6(a)对比可知，相比于始发直观模式，两者仅在正向变形程度上有所区别，整体构型基本一致.图11(a)为混合变形模式薄板中心点(A点)与靠近边缘处一点(B点)的挠度变化历程.薄板边缘区域在极值点反向屈曲后停留在负方向，发生反直观行为；而中心区域始终在正方向运动，发生直观行为.图11 (b)为薄板混合模式中线构型，其中心区域向正方向凸出，边缘区域向负方向凹入.混合模式表明薄板的不同区域可以同时发生直观行为与反直观行为.

表3 距离当量比Z=1.809m/kg1/3时不同爆炸距离R下薄板变形模式Table 3 Deformation mode of thin plate under different explosion distance R when scaled distance Z=1.809m/kg1/3

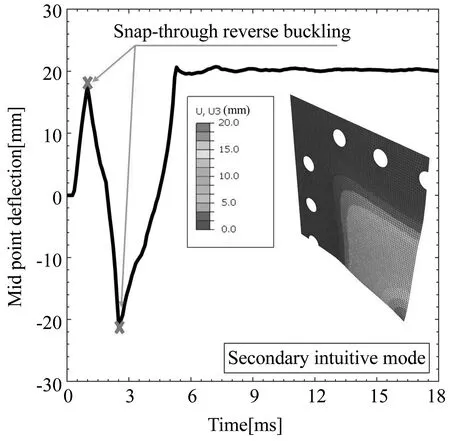
(a) 继发直观模式薄板中心挠度变化历程(a) Variation history of central deflection in Secondary intuitive mode

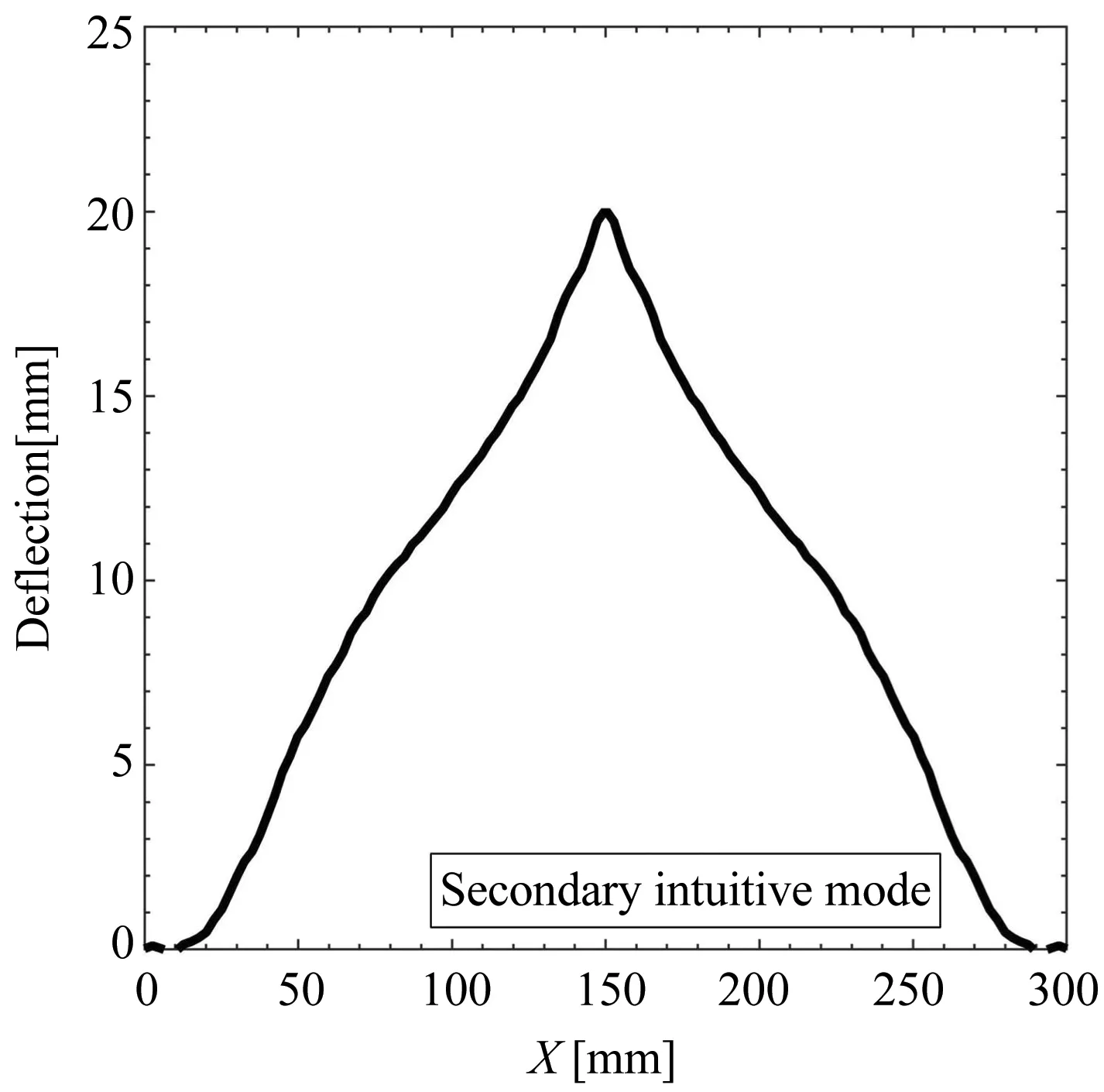
(b) 继发直观模式薄板中线构型(b) Final configuration of thin plate centerline in Secondary intuitive mode图10 薄板继发直观变形模式Fig.10 Secondary intuitive deformation mode of thin plate

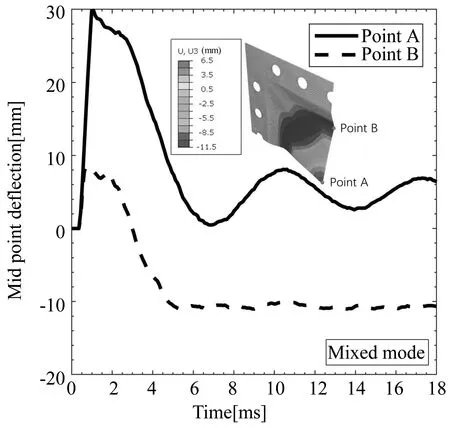
(a) 混合模式薄板中心及边缘挠度变化历程(a) Variation history of center and edge deflection of thin plate in mixed mode

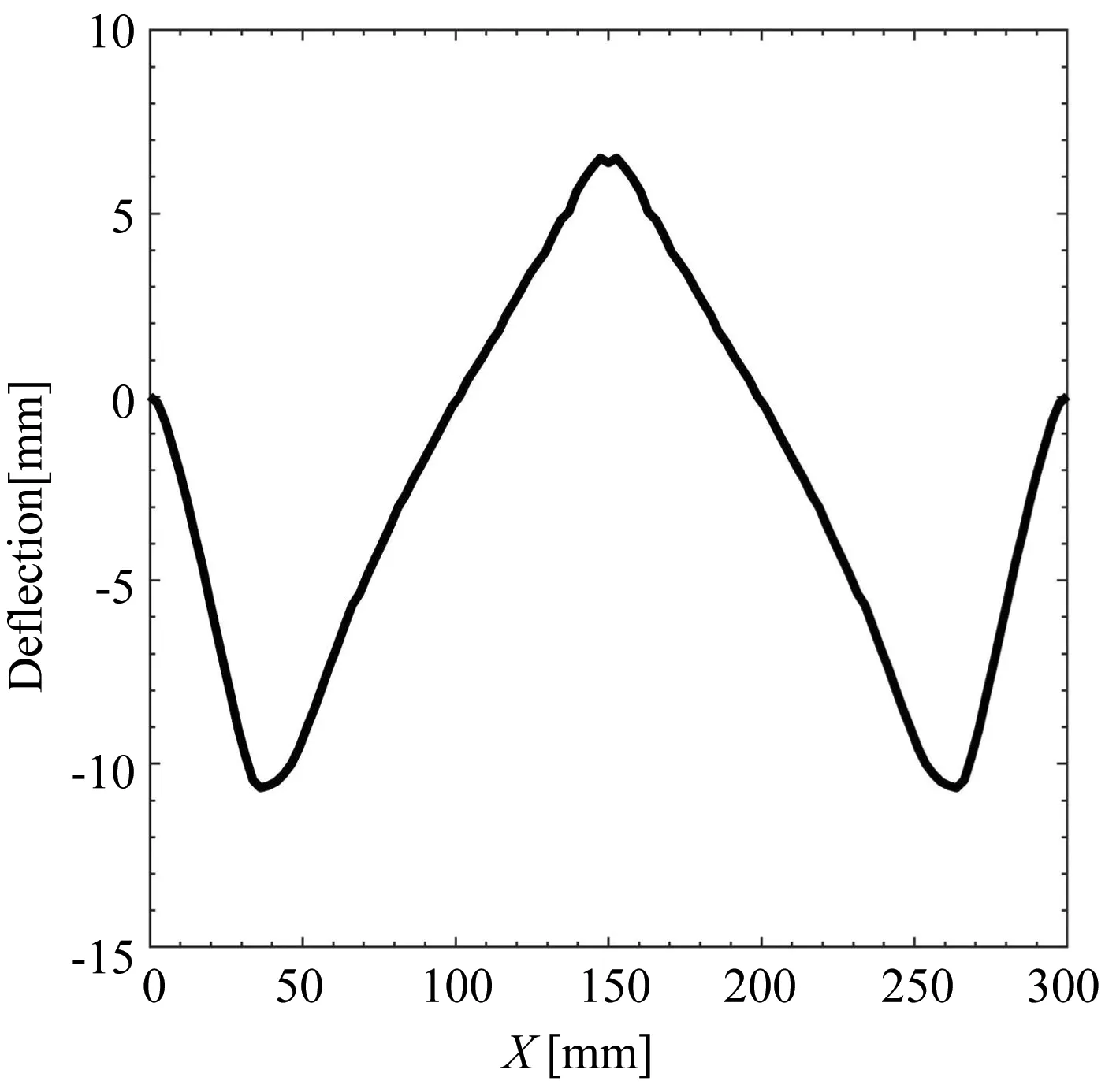
(b) 混合模式薄板中线构型(b) Mixed mode centerline configuration of thin plate图11 薄板混合变形模式Fig.11 Mixed deformation mode of thin plate

综上，继发直观模式发生多于一次的极值点反向屈曲；反直观模式发生一次极值点反向屈曲；混合模式薄板边缘区域发生一次极值点反向屈曲；始发直观模式没有发生极值点反向屈曲.

当Z减小至1.6m/kg1/3时，在R=375mm的情况下反直观模式替代了原有的继发直观模式；在R=625mm的情况下始发直观模式替代了原有的反直观模式.根据表3的规律可以预测在Z=1.6m/kg1/3的情况下R=425mm-575mm区间内必然存在一个R的范围使薄板发生混合变形模式.通过验证得到R=500mm时薄板发生混合变形模式.薄板变形模式总结如表 4所示.

表4 距离当量比Z=1.6m/kg1/3时不同爆炸距离R下薄板变形模式Table 4 Deformation mode of thin plate under different explosion distance R when scaled distance Z=1.6m/kg1/3

表3和表4结果表明当距离当量比Z一定时，薄板在爆炸冲击载荷下存在顺序固定的四种变形模式.爆炸距离R较小时，首先发生继发直观模式，随着爆炸距离R的递增，依次发生反直观模式、混合模式、始发直观模式，而且这四种变形模式并不随着爆炸距离R等间隔变化.

4.2 薄板响应模式机理分析

薄板不同变形模式塑性耗散能的演化过程有所不同.继发直观模式下塑性耗散能发生三次抬升，与薄板的初次正向变形、回弹及再次正向变形相对应,如图12(a)所示；反直观与混合模式下塑性耗散能在薄板回弹过程同样存在抬升，如图12(b)(c)所示；直观模式下塑性耗散能在初始阶段快速上升后保持平稳，如图12(d)所示.各图中A阶段塑性耗散能的初始快速抬升阶段对应薄板初次正向变形.B阶段与C阶段均发生极值点反向屈曲，其中B阶段塑性耗散能缓慢上升对应薄板的回弹阶段，C阶段塑性耗散能进一步缓慢上升对应薄板的再次正向变形阶段.A阶段薄板初次正向变形产生的塑性耗散能在整个变形过程中占比最多，后续B阶段与C阶段极值点反向屈曲过程占比较少.

(a) 继发直观模式(a) Secondary intuitive mode

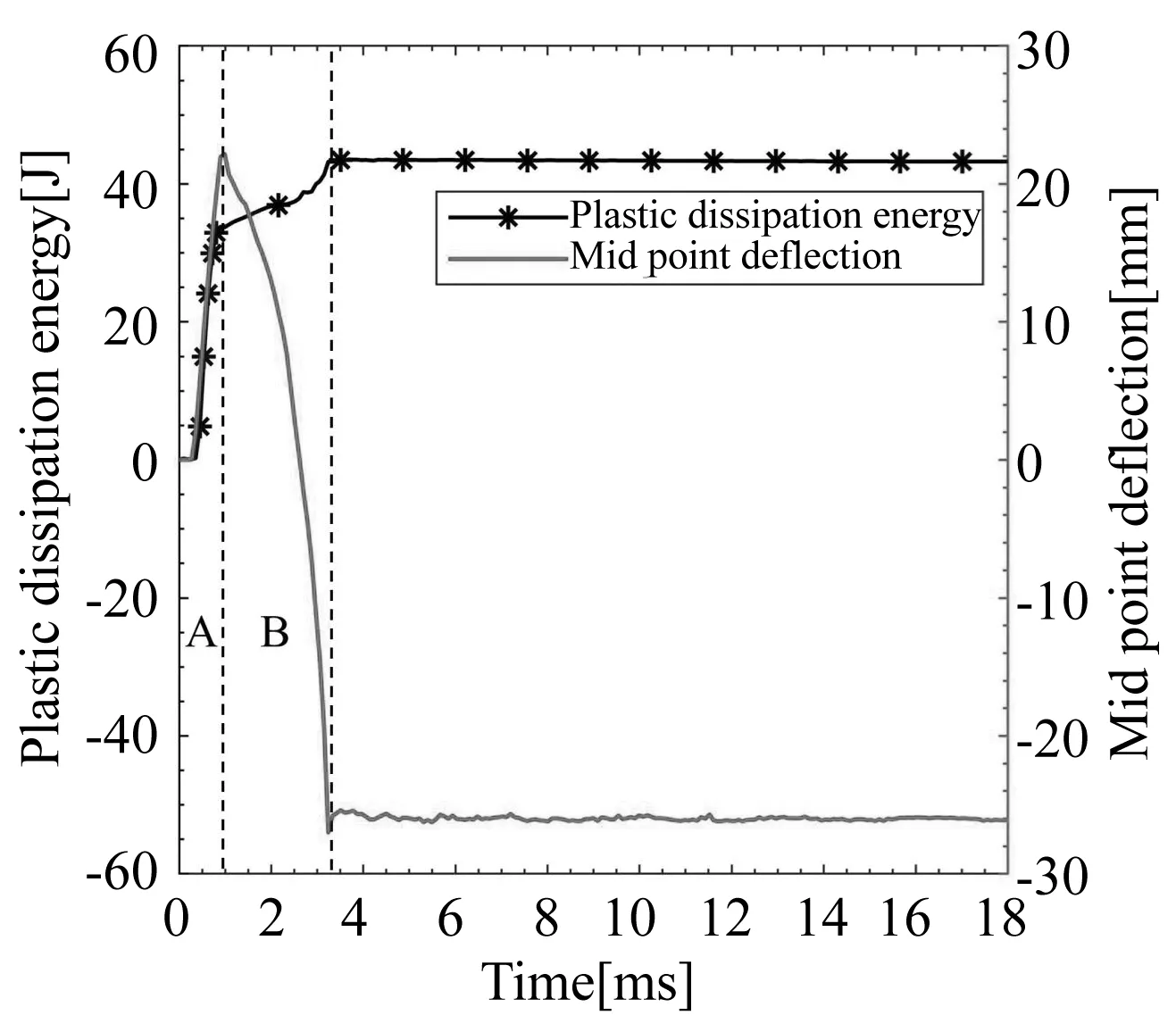
(b) 反直观模式(b) Counter-intuitive mode

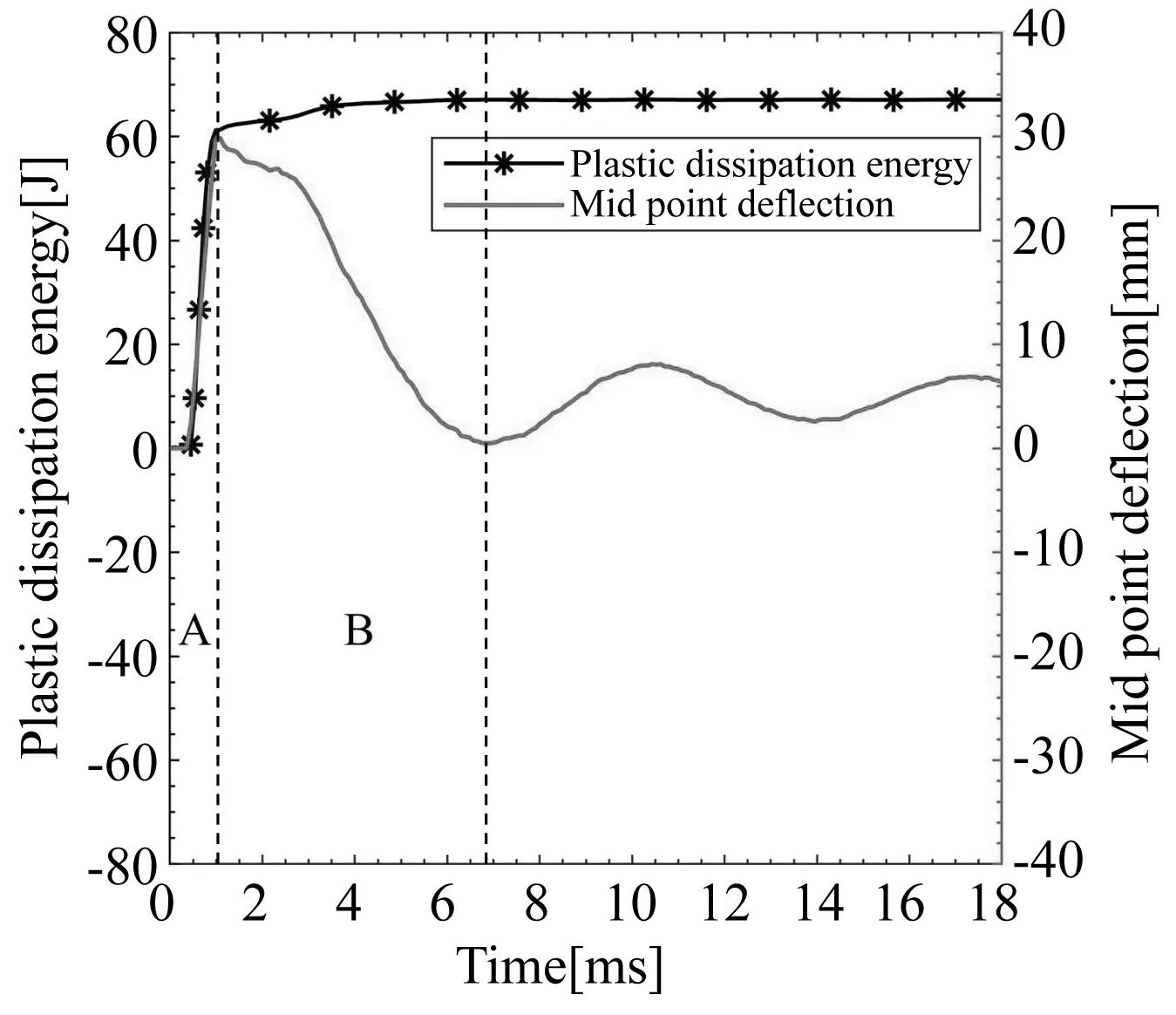
(c) 混合模式(c) Mixed mode

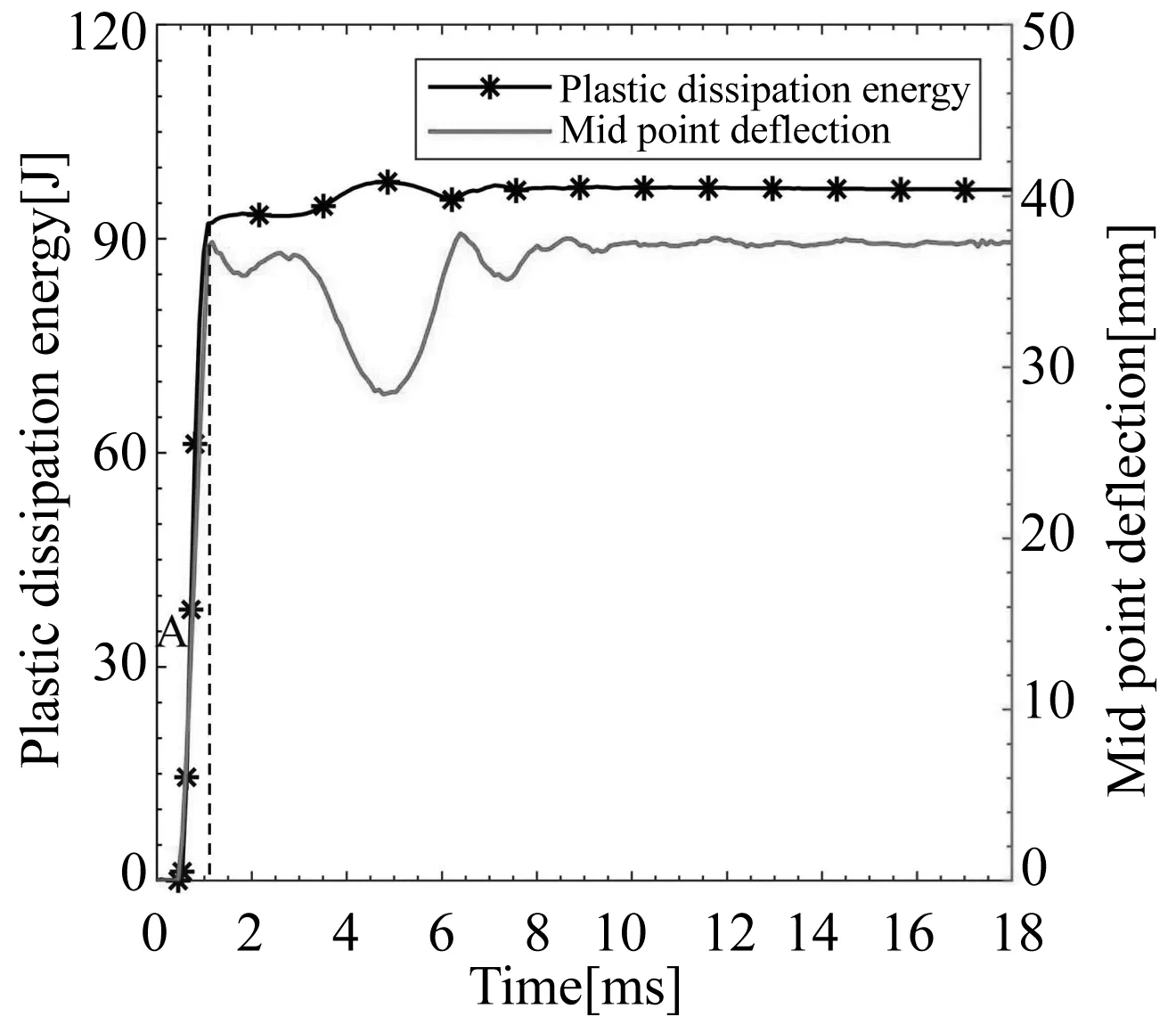
(d) 始发直观模式(d) Initial intuitive mode图12 薄板动力行为模式与塑性耗散能关系Fig.12 Relationship between dynamic behavior mode of thin plate and plastic dissipated energy

当较低冲量造成的薄板初次正向变形较小，无法将冲击波提供能量完全耗散时，薄板会在负压的激励下发生回弹并发生继发直观模式，回弹与再次正向变形过程塑性耗散进一步增加，导致薄板在经历多次变形后最终停留在正方向.随着冲击波冲量的增加，薄板初次正向变形增加，塑性耗散增加，薄板仅需初次正向变形和回弹两个阶段即停止变形并最终停留在负方向，表现出反直观模式.同理，在冲量进一步增加后，薄板初次正向变形的塑性功耗散足以使薄板停止变形，即发生始发直观模式.而引起混合模式的冲击波冲量介于反直观模式与始发直观模式之间，该冲量范围内只能使薄板边缘区域发生回弹.

综上，爆炸冲击载荷下薄板发生何种变形模式取决于初次正向变形塑性功耗散多少.初次塑性耗散能越少则极值点反向屈曲越多；初次塑性耗散能越多则极值点反向屈曲越少.

5 结论

本文讨论内容与爆炸载荷负压关系密切，爆炸载荷距离当量比较大时负压对结果有着显著影响，因此相关结论的适用范围也是在距离当量比较大的情况下.

(1)尽管爆炸冲击载荷的负压压强相对较小，但其对于薄板反直观异常行为的发生至关重要.

(2)爆炸冲击载荷负压段的描述方式对薄板反直观异常动力行为的响应历程有着显著影响.

(3)爆炸冲击载荷正压衰减过程影响薄板反直观行为的最大挠度与回弹过程持续时间.

(4)在距离当量比一定时，随着爆炸距离的增加，薄板依次发生继发直观、反直观、混合、始发直观四种行为模式.这种现象发生的原因是薄板不同正向变形程度的塑性耗散强弱不同，变形程度越小、塑性耗散越少，则越容易发生极值点反向屈曲.