耦合pre-Bötzinger复合体中放电模式的动力学分析*

齐会如 段利霞 徐浩

(北方工业大学 理学院，北京 100144)

引言

呼吸运动是哺乳动物维持生命的关键行为之一，主要由简单的节律性运动组成. 呼吸节律的产生一直受到研究者的广泛关注. 1991年，Smith等,对新生大鼠进行实验研究，确定了新生儿神经系统腹外侧髓质中一个非常有限的区域，pre-Bötzinger复合体(简称为pre-BötC)能够产生呼吸节律[1]. 随后，一些研究表明pre-BötC也存在于成年大鼠和猫的延髓[2,3]. 因为pre-BötC存在兴奋性神经元，包括吸气神经元，所以呼吸可以自主、有节律地发生. 吸气神经元和其他呼吸组织一同协调和控制呼吸节律[4].

1999年，Butera等人提出两种最小神经元模型，发现簇放电的产生都与持续钠电流(INaP)有关[5,6].之后的研究还发现pre-BötC神经元大多具有持续钠电流(INaP)[7]和钙激活的非特异性阳离子电流(ICAN)[8]，且ICAN对吸气驱动电位和呼吸节律的发生起着重要作用[8,9]. Degro等人发现INaP和ICAN可以增强神经元的兴奋性，并促进节律发生[10]. Rubin等人提出一个新的数学模型用于研究基于ICAN的节律发生机制，分析发现ICAN引起的鲁棒去极化会导致电压依赖性的尖峰失活，而尖峰的衰减会产生突触抑制使ICAN失活[11]. Toporikova和Butera提出了一种具有两个独立簇放电机制的孤立神经元的双室数学模型(TB 模型)[12]，他们认为树突中的簇放电依赖于细胞内钙离子浓度，且SERCA泵的最大活性(VSERCA)影响簇放电的频率. 随后，Park和Rubin简化了TB 模型，建立了pre-BötC神经元单室模型[13]，并给出了胞体簇、树突簇和胞体—树突簇的产生机理和影响因素.

混合簇放电模式是指在一个周期内包含多种类型的簇放电，其产生机制与不同的时间尺度有关，涉及极为复杂的动力学特征. 钙激活的非特异性阳离子电流ICAN在混合簇的产生中起着重要作用[14,15]. 分岔理论[16,17]和几何奇异摄动理论[18-20]等是研究簇放电模式的常用方法. Izhikevich使用分岔分析，从动力学的角度揭示了神经元放电活动的特征，并将簇放电进行了归纳和分类[21]. 持续钠电流INaP和钙激活的非特异性阳离子电流ICAN共同作用会使方波簇和去极化阻滞簇交替出现，且该作用有助于混合簇放电模式的出现[22].Duan等人研究了耦合pre-BötC神经元中同相簇放电、反相簇放电以及混合簇放电模式[23-25]. Lü等人研究了钠电导(gNa)和钾电导(gK)变化对pre-BötC混合簇放电模式的影响，并阐明了钾电导(gK)和漏电导(gL)对胞体簇放电个数的影响[26]. 刘深泉等人对前包钦格复合体、内嗅皮层的星状细胞和基底神经节中的神经元进行了动力学研究[27,28]. 陆孟盼等研究了具有电流反馈的两房室锥体神经元，并对其同步簇放电进行动力学分析[29]. 古华光等运用电生理实验及理论模型，借助分岔分析揭示了外部刺激和负反馈对神经元动力学行为的复杂转迁机制[30,31]. 近年来，Wang等研究了胚胎呼吸神经元随持续钠电导和钙激活的非特异性阳离子电导变化而产生的不同簇放电模式[32].Lü等发现混合簇也可以由树突引起的细胞内钙振荡驱动，并研究了几种特殊的树突混合簇放电[33]. 虽然关于混合簇放电的研究有了一些结果，但在耦合神经元中，混合簇放电的产生机理及树突子系统对放电模式的影响仍值得进一步研究.

本文的结构如下：首先，介绍了耦合pre-BötC神经元的数学模型；其次，分析了模型中树突子系统的动力学特性，并运用快慢分析、单参数和双参数分岔分析，探究了钙激活的非特异性阳离子电导(gCAN)以及钙动力学参数VSERCA对pre-BötC中混合簇放电模式的影响，并给出了簇放电转迁的动力学机制；最后，给出本文的结论.

1 模型

本文分析了Toporikova和Butera于2011年建立的耦合pre-BötC神经元模型(简称TB模型)[12]，模型描述如下：

dVi/dt=(-INa-INaP-IK-ICAN-

IL-Isyn-e)/Cm

(1)

dhi/dt=ε(h∞(Vi)-hi)/τh

(2)

dni/dt=(n∞(Vi)-ni)/τn(Vi)

(3)

dsi/dt=αs(1-si)s∞(Vj)-si/τs

(4)

d[Ca]i/dt=fm(JERIN-JEROUT)

(5)

dli/dt=AKd(1-li)-A[Ca]ili

(6)

其中i、j∈{1，2}，且i≠j.Cm为膜电容，Vi表示膜电位，hi和ni是门控变量，si是突触耦合变量，[Ca]i表示细胞内钙离子浓度，其浓度由从ER进入胞浆的通量(JERIN)和从胞浆流入ER的通量(JEROUT)决定，li表示未被灭活的IP3通道的部分.INa，INaP，IK,ICAN,IL和Isyn-e分别表示钠电流、钾电流、持续钠电流、钙激活的非特异性阳离子电流、漏电流以及耦合神经元网络所产生的突触电流. 各离子电流的表达式如下：

INaP=gNaPmp∞(Vi)hi(Vi-ENa)

ICAN=gCANf([Ca]i)(Vi-ENa)

IL=gL(Vi-EL)

Isyn-e=gsyn-esi(Vi-Esyn-e)

方程(1)-(6)称为全系统，方程(1)-(3)称为胞体子系统，方程(5)-(6)为钙动力学表达式，称为树突子系统[13]，方程(4)为神经元之间的耦合关系.在钙动力学中，f([Ca]i)，JERIN和JEROUT的表达式为：

f([Ca]i)=1/(1+(KCAN/[[Ca]]i)nCAN)

([Ca]ER-[Ca]i)

模型中其他变量的表达式及参数值见附录.

2 主要结果

在耦合pre-BötC神经元模型中，相同参数集下，初始条件相同时系统会产生同相簇放电，当初始条件不同时，系统会产生反相簇放电[24,34]. 本文的研究只关注同相簇放电，此时，取定V1=V2，[Ca]1=[Ca]2，h1=h2和l1=l2，故下文中只提及V1,[Ca]1,h1,l1.

2.1 树突子系统中的钙动力学

树突子系统(5)-(6)可视为TB模型的激励系统，其动力学行为对全系统的节律输出有重要的影响. 首先，我们研究树突子系统(5)-(6)的动力学行为. 树突子系统(5)-(6)相对于参数VSERCA的分岔分析如图1(a)所示，其中黑色曲线由平衡点组成，红色曲线表示极限环的最大值和最小值.F1、F2表示平衡点的鞍结分岔，subH表示亚临界Hopf分岔，LPC表示极限环的鞍结分岔.

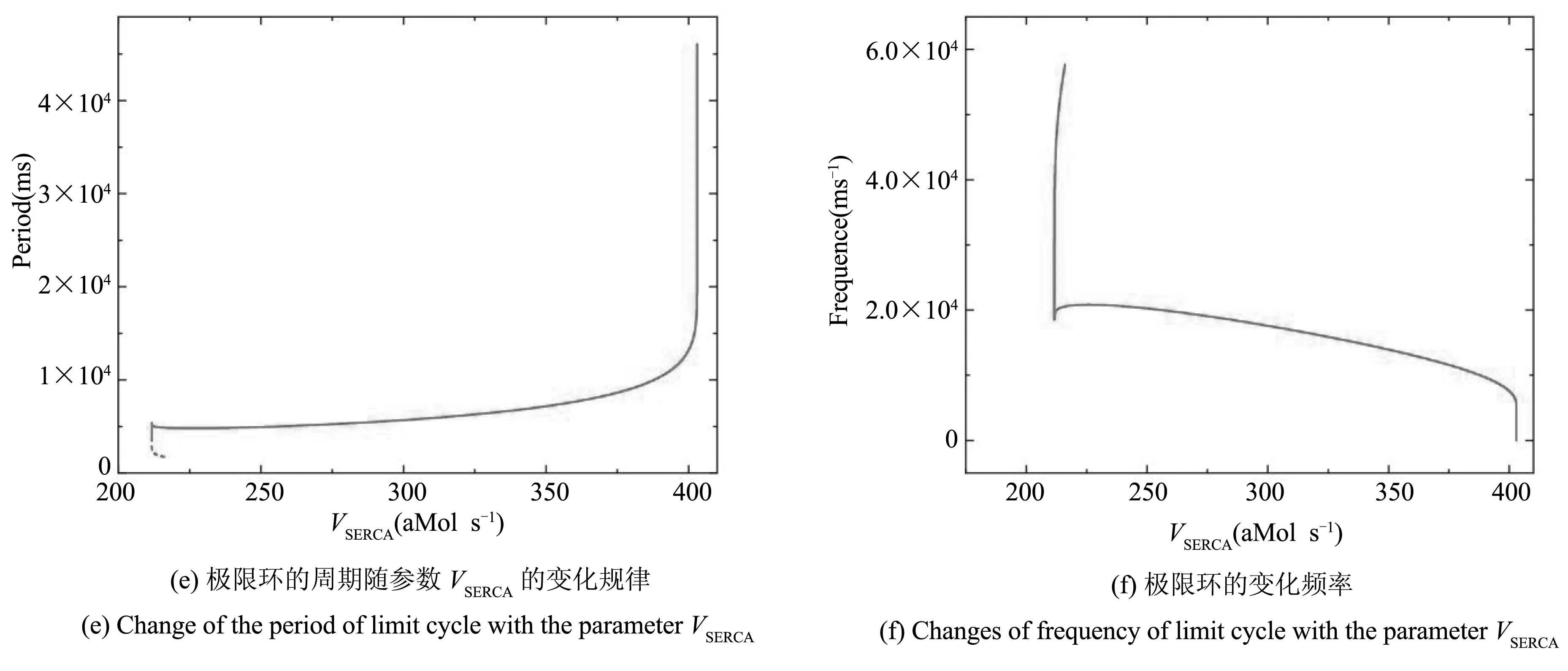
图1 参数VSERCA变化时树突子系统的动力学分析Fig.1 Dynamics of the dendritic subsystem with VSERCA

当VSERCA=216.07aMol·s-1时，亚临界Hopf分岔(subH1)产生，同时不稳定极限环(LPC之间的虚线)产生. 当VSERCA=211.64aMol·s-1时，由于极限环的鞍结分岔(LPC)产生，不稳定极限环转变为稳定极限环(LPC之后的实线). 平衡点的下支的亚临界Hopf分岔点(subH2)处也产生不稳定的极限环，如图1(b)所示. 当VSERCA=402.75aMol·s-1时，树突子系统存在一个稳定极限环(SLC)和一个不稳定极限环(ULC)，如图1(c)所示，钙离子浓度[Ca]1和l1的零等值线(绿色和红色曲线)也叠加在图中. 随着VSERCA的增加，不稳定极限环的振幅逐渐增加且距离稳定极限环越来越近，如图1(d)所示(此时VSERCA=402.81aMol·s-1). 故当VSERCA=402.9aMol·s-1时，稳定极限环和不稳定极限环相遇并经由极限环的鞍结分岔(LPC)消失.

随着VSERCA的增加，极限环周期增加而频率减小，即当VSERCA=216.07aMol·s-1时，亚临界Hopf分岔点(subH1)处极限环产生，此时极限环周期最小. 随着VSERCA的增加，周期逐渐增大. 当VSERCA=402.9aMol·s-1时，稳定极限环经由极限环的鞍结分岔(LPC)消失，周期趋近于无穷大，如图1(e)所示. 随着VSERCA的增加，频率逐渐减小，如图1(f)所示.

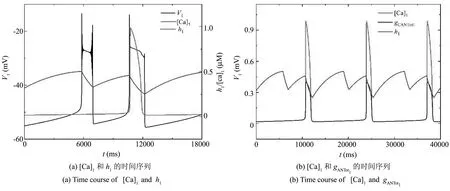
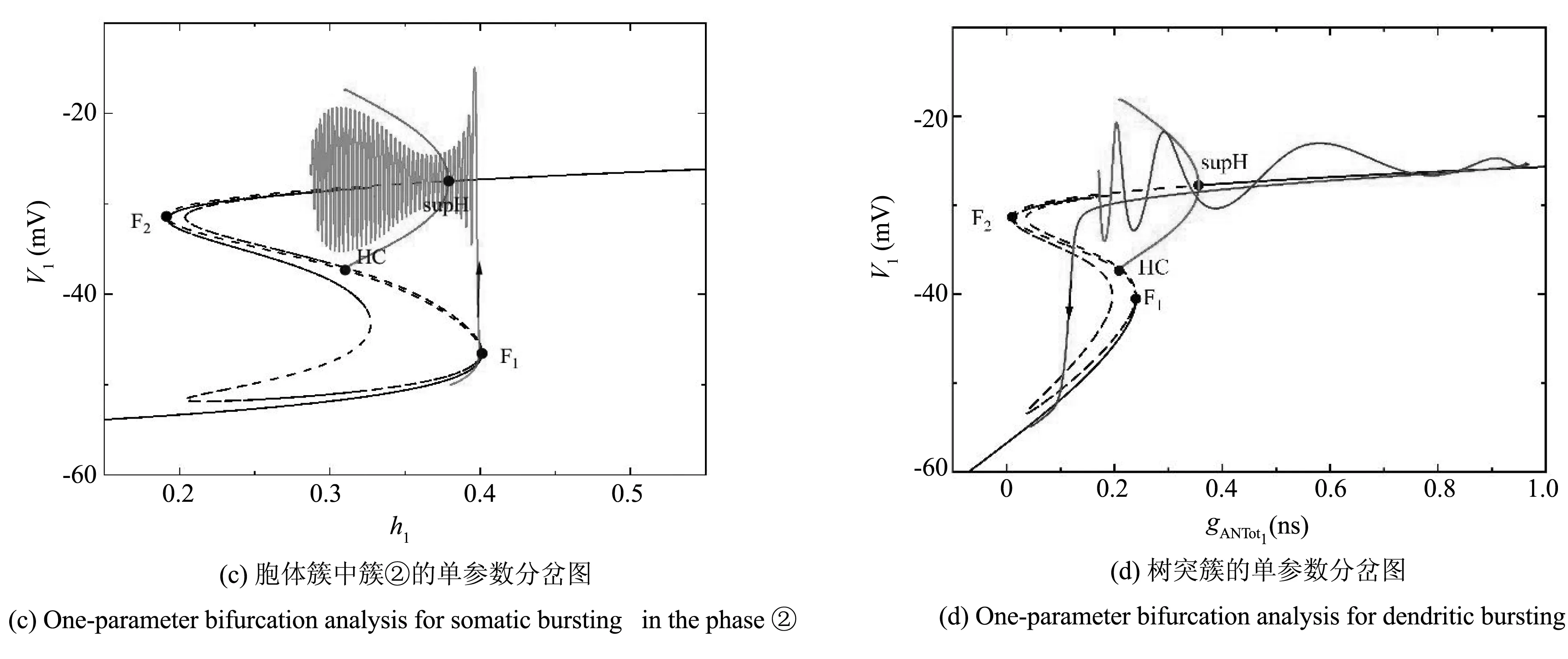
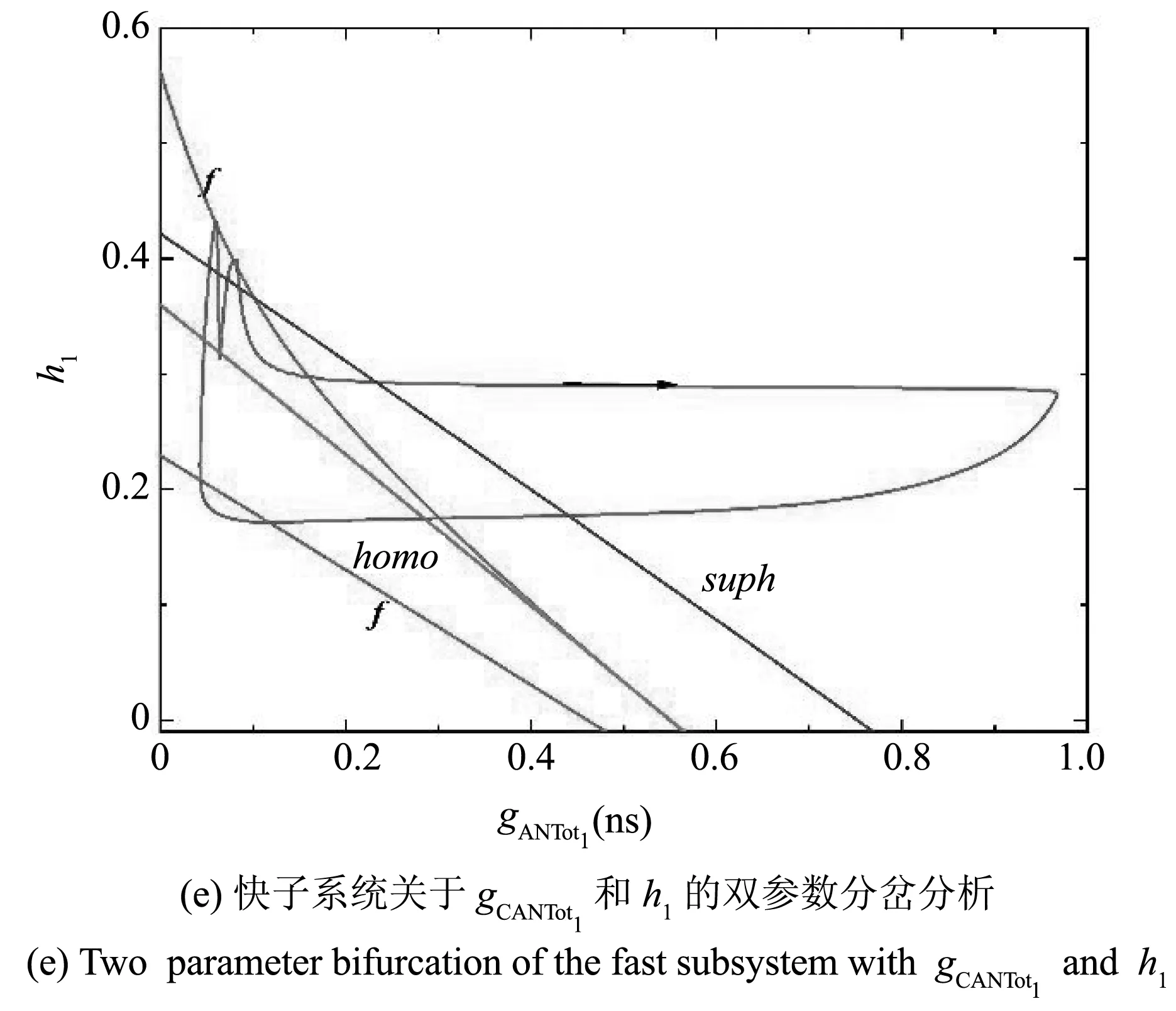
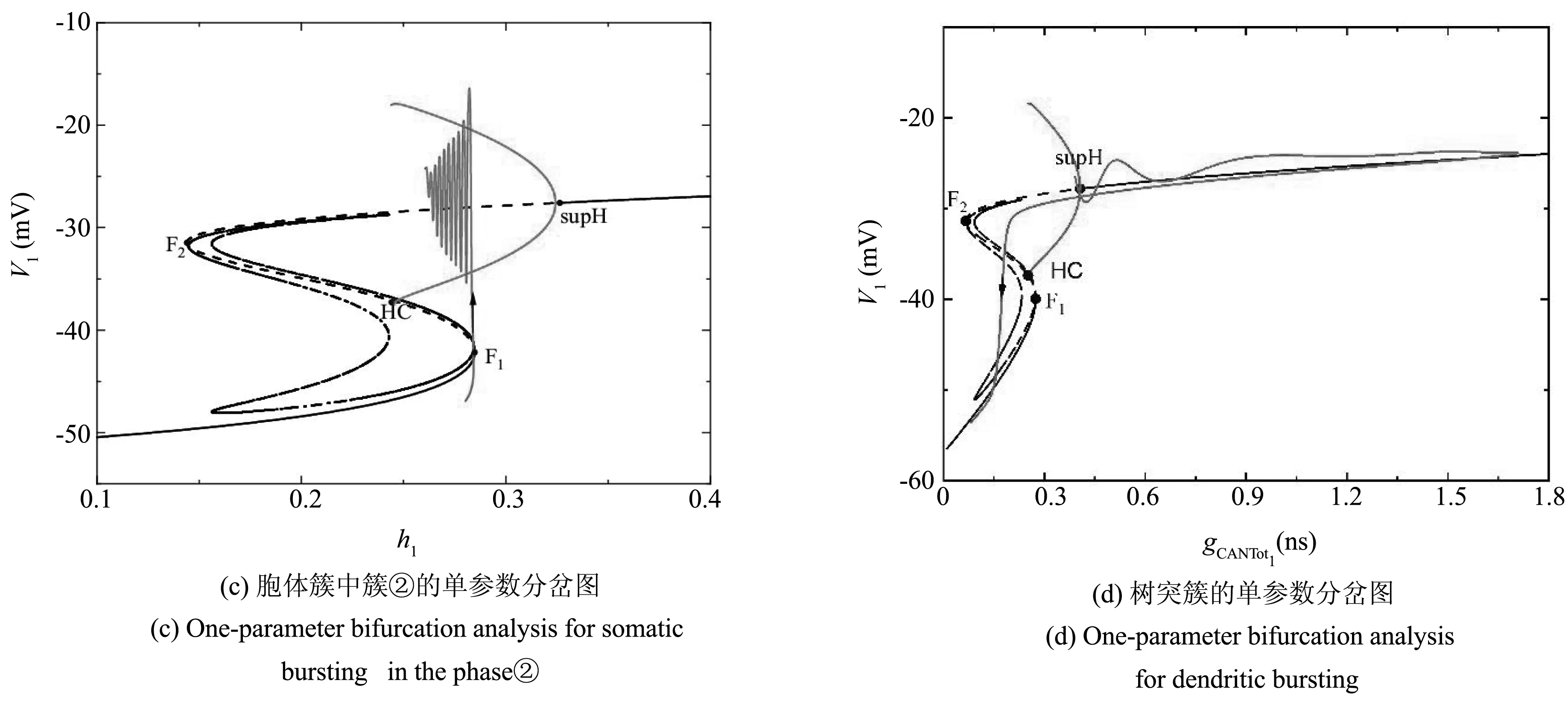
由以上的动力学分析知，当211.64aMol·s-1

2.2 gCAN对pre-BötC中簇放电模式的影响

当211.64

图2 不同gCAN下系统表现的放电模式和ISI分岔Fig.2 Firing patterns and ISI bifurcation of the system with different gCAN

参数gCAN变化时对应膜电位的ISI(峰峰间期)分岔序列如图2(b),图2(c)所示. 我们只研究0ns

在系统(1)-系统(6)中，V1，n1和s1为快变量，[Ca]1和h1为慢变量，l1为超慢变量. 由于胞体子系统直接受[Ca]1的影响，而不受l1的影响，所以在接下来的分析中，只考虑两个慢变量[Ca]1、h1. 膜电位V1为周期性簇放电时，变量[Ca]1有相应的周期性波动，如图3(a)所示. 当gCAN=0.7ns时，[Ca]1和h1的时间序列如图3(b)所示. 钙离子浓度呈周期性波动变化，它包括两个阶段：静息阶段和尖峰放电阶段. 在静息阶段，钙离子浓度的值几乎是一个常数. 此时，钙离子浓度可以被看作一个常数，取其静息阶段的平均值([Ca]1=0.023925)，将h1作为慢变量. 在尖峰放电阶段，钙离子浓度的值变化较大，而h1的变化相对较小，故在此阶段，h1可看作一个常数, [Ca]1为慢变量. 引入辅助变量gCANToti=gCANf([Ca]i)，其中f([Ca]i)是[Ca]i的一个单调递增的下凹函数.gCANToti保持了与[Ca]i相同的动态特性(除振幅外)，如图3(b)所示. 因此，在快慢分析中，当[Ca]1为慢变量时，可以直接使用gCANTot1代替[Ca]1作为分岔参数.

图3 gCAN=0.7ns时，不同参数对应的时间序列Fig.3 Time series of different parameter at gCAN=0.7ns

当gCAN=0.7ns时，膜电位V1随时间t的变化如图4(a)所示(实线)，系统呈现混合簇放电模式. 在胞体簇放电阶段，[Ca]1和l1为常数，取[Ca]1=0.023925. 快子系统(1)-(3)对慢变量h1的分岔如图4(b)所示，其中黑色曲线由平衡点组成，曲线的下支由稳定结点(实线)组成，上分支由不稳定焦点(虚线)和稳定焦点(实线)组成，不稳定焦点经超临界Hopf分岔(supH)变为稳定焦点，且在Hopf分岔处产生稳定的极限环(实线). 曲线的中支由鞍点(虚线)组成. 点F1和F2为平衡点的鞍结分岔. 胞体簇放电在(h1,V1)平面上的投影也叠加在快子系统相应的分岔图上. 系统轨线的下状态即静息态经由平衡点的鞍结分岔F1跃迁到曲线上支，由于稳定焦点的吸引，轨线围绕稳定焦点作振幅逐渐减小的振荡. 当轨线经过超临界Hopf分岔(supH)时，由于不稳定焦点的排斥和稳定极限环的吸引作用，轨线的振幅逐渐增大并最终经由同宿轨分岔(HC)跃迁至下支的稳定结点. 静息态经由supH转变为放电态，而放电态又经同宿轨分岔(HC)转变为静息态，从而形成一个经由“fold/homoclinic”滞后环的“Hopf/homoclinic” 型簇放电.

图4 gCAN=0.7ns的动力学分析Fig.4 The dynamic analysis of gCAN=0.7ns

在第二阶段的放电部分，将h1看作常数(取平均值)，取h1=0.339356，快子系统(1)-(3)对慢变量gCANTot1的分岔如图4(c)所示，该部分对应的第二个簇放电的轨迹也叠加在分岔图中. 随着gCANTot1的增加，轨线从下状态跃迁至上状态，由于稳定极限环的吸引，振幅逐渐减小，并通过超临界Hopf分岔(supH). 又由于稳定焦点的吸引，轨线振幅进一步减小. 当gCANTot1增至最大值时又迅速减小. 最终轨线经过同宿轨分岔回到静息状态.

快子系统(1)-(3)对慢变量gCANTot1和h1的双参数分岔如图4(d)所示，全系统的相图也叠加在分岔图上. 其中，双参数分岔曲线包括鞍结分岔f，超临界Hopf分岔suph和同宿轨分岔homo. 当h1的值较小时即图4(d)三角形(▲)处，gCANTot1的变化很小([Ca]1也是如此). 轨线在鞍结分岔曲线(f)和同宿轨分岔曲线(homo)之间跃迁一次，对应于混合簇放电中的胞体簇放电的个数. 之后gCANTot1突然向右增加，系统由胞体簇放电转迁为树突簇放电，最终经由同宿轨分岔(homo)回到静息态，从而完成一个混合簇放电周期.

当gCAN=1.7ns时，膜电位V1随时间t的变化如图5(a)所示，系统呈现混合簇放电，按照钙离子浓度[Ca]1的变化情况将整个周期分为两个阶段. 快子系统(1)-(3)对慢变量h1的单参数分岔如图5(b)，5(c)所示. 在簇①中，取[Ca]1=0.023712，神经元的放电模式与gCAN=0.7ns中胞体簇部分的放电模式相同，为“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电；在簇②中，由于钙离子浓度处于平稳阶段，仍以h1做慢变量，取[Ca]1=0.032029，快子系统(1)-(3)对慢变量h1的分岔如图5(c) 所示，系统轨线的下状态即静息态经由平衡点的鞍结分岔F1跃迁到上状态，受稳定焦点的吸引，轨线振幅逐渐减小. 轨线经过超临界Hopf分岔(supH)后，受极限环的吸引振幅逐渐增大. 由于钙离子浓度的突然增加，轨线没有回到静息态，而是直接进入树突簇放电阶段，在此阶段，慢变量为gCANTot1，取h1=0.224166, 快子系统对慢变量gCANTot1的分岔如图5(d)所示，轨迹经过超临界Hopf分岔(supH)，向右移动. 由于稳定焦点的吸引振幅逐渐减小，最终经由HC分岔，系统回到静息态.

图5 gCAN=1.7ns的动力学分析.Fig.5 The dynamic analysis of gCAN=1.7ns

快子系统(1)-(3)对慢变量gCANTot1和h1的双参数分岔如图5(e)所示，全系统的相图也叠加在图上. 当gCAN=1.7ns时，混合簇放电的动力学机制与gCAN=0.7ns时的情形相似，此处不再详述.

当gCAN=3ns时，膜电位V1随时间t的变化如图6(a)所示，系统呈现混合簇放电. 在胞体簇放电阶段，把h1看慢变量，[Ca]1取平均值，快子系统(1)-(3)对慢变量h1的分岔如图6(b)，6(c)所示,其中7(b)对应的时间序列为阶段①，取[Ca]1=0.023565，系统轨线下支的静息态经由平衡点的鞍结分岔F1跃迁到上状态，受极限环的吸引发生振荡，放电态经由极限环的同宿轨分岔(HC)转迁为静息态. 因此，放电模式为“fold/homoclinic”型簇放电. 图6(c)对应阶段②的放电模式，取[Ca]1=0.041379，系统轨线从静息态经由平衡点的鞍结分岔F1跃迁到上状态，受极限环吸引发生振荡，由于钙离子浓度增大，轨线没有回到静息态，而是直接进入树突簇放电部分，如图6(d) 所示，在此部分取h1=0.196341，gCANTot1为慢变量，此部分的动力学机制与gCAN=1.7ns时的情形相似，此处不再详述.

图6 gCAN=3ns的动力学分析Fig.6 The dynamic analysis of gCAN=3ns

快子系统(1)-(3)对慢变量gCANTot1和h1的双参数分岔如图6(e)所示. 在gCANTot1突增之前，轨线在鞍结分岔曲线(f)和同宿轨分岔曲线(homo)之间跃迁两次，意味着混合簇放电中有两个胞体簇. 之后gCANTot1突然向右增加，系统由胞体簇放电转迁为树突簇放电，然后经过超临界Hopf分岔(supf)，鞍结分岔(f)和同宿轨分岔(homo)曲线并回到静息态，从而完成一次混合簇放电.

当gCAN=9ns时，膜电位V1随时间t的变化如图7(a)所示，树突部分出现尖峰放电，考虑树突部分的单参数分岔，如图7(b)所示，取h1=0.054535，gCANTot1为慢变量，放电模式在胞体簇部分没有回到静息态而是直接进入树突部分，轨迹向右运动，经过超临界Hopf分岔(supH)，由于稳定焦点的吸引，最终回到静息态.

图7 gCAN=9ns的动力学分析Fig.7 The dynamic analysis of gCAN=9ns

快子系统(1)-(3)对慢变量gCANTot1和h1的双参数分岔如图7(c)所示. 随着gCANTot1的增加，系统轨迹在鞍结分岔曲线(f)和同宿轨分岔曲线(homo)之间跃迁三次，第三次跃迁被gCANTot1的突然增加中断，这对应于混合簇放电中的前两个胞体簇和最后一个树突簇(如图7(a)).

当gCAN=15ns时，膜电位V1随时间t的变化如图8(a)所示，膜电位的振幅减小，以gCANTot1为慢变量，取h1=0.041314，快子系统(1)-(3)对慢变量gCANTot1的分岔如图8(b)所示，系统轨线在(gCANTot1,V1)平面上的投影也叠加在图中. 系统轨线经由超临界Hopf分岔(supH)，在稳定极限环的吸引下由静息态转迁至振荡态，由于稳定焦点的吸引，振幅减小，最终经由HC分岔，轨线回到下支的静息态.

快子系统(1)-(3)对慢变量gCANTot1和h1的双参数分岔如图8(c)所示. 轨线在分岔曲线f和homo之间没有来回跃迁，而是直接进入树突部分，系统没有完整的胞体簇放电.

图8 gCAN=15ns的动力学分析Fig.8 The dynamic analysis of gCAN=15ns

当gCAN=30ns时，全系统的膜电位V1随时间t的变化如图9(a)所示，轨线在平衡点曲线的上分支作周期运动，即神经元的放电模式变为峰放电. 以gCANTot1为慢变量，h1=0.010956，快子系统(1)-(3) 与慢变量gCANTot1的分岔分析如图9(b)所示，伴随[Ca]1的振荡，膜电位存在一个小的振荡，即峰放电(图9(a)).

图9 gCAN=30ns的动力学分析Fig.9 The dynamic analysis of gCAN=30ns

快子系统(1)-(3)对慢变量gCANTot1和h1的双参数分岔如图9(c)所示. 轨线不再通过鞍结分岔曲线f、超临界Hopf分岔曲线suph和同宿轨分岔曲线homo，故此时系统没有胞体簇放电，仅有树突峰放电.

2.3 VSERCA对pre-BötC簇放电模式的影响

本节我们研究当gCAN=3ns时，参数VSERCA对神经元放电模式的影响. 当VSERCA增加时，系统的放电模式如图10(a)所示. 随着VSERCA的增加，全系统(1)-(6)的放电模式从静息状态过渡到混合簇放电状态.

图10 不同VSERCA下系统表现的放电模式和ISI分岔Fig.10 Firing patterns and ISI bifurcation of the neuron model with VSERCA

全系统(1)-(6)关于参数VSERCA的ISI分岔序列如图11(b)所示，其中虚线分别对应VSERCA=211.64aMol·s-1和VSERCA=402.9aMol·s-1，分别表示神经元由静息到放电以及由放电到静息的两个临界值. 当VSERCA∈(211.64,402.9)时，随着VSERCA的增加，其峰峰间期逐渐增加，且神经元的放电模式也在变化. 当VSERCA增加到370aMol·s-1，神经元有一个胞体簇，当VSERCA进一步增加到398aMol·s-1，胞体簇的个数变为两个. 当VSERCA<211.64aMol·s-1和VSERCA>402.9aMol·s-1，神经元处于静息态，钙离子浓度以及膜电位不再变化.

3 结论

对pre-BötC神经元的混合簇放电模式已有大量研究，大多数研究认为这种混合簇放电依赖于持续钠电流(INaP)和钙激活的非特异性阳离子电流(ICAN)的共同作用. 本文仅考虑ICAN对pre-BötC神经元放电模式的影响. 电流ICAN受到gCAN和细胞内钙离子的影响，实验发现SERCA泵可以转运Ca2+和调节细胞内钙稳态[35]，进而影响[Ca]1和ICAN. 所以本文主要考虑gCAN和VSERCA对pre-BötC神经元放电模式的影响.

为了探究电流ICAN对模型中混合簇放电模式的影响，本文首先对树突子系统的钙动力学进行单参数分岔分析，给出了参数VSERCA对钙离子浓度[Ca]1的影响. 当VSERCA∈(211.64,402.9)时，[Ca]1发生周期性波动，全系统表现出复杂的动力学行为. 本文选取VSERCA=400aMol·s-1，研究gCAN对耦合pre-BötC神经元放电模式的影响，并从动力学角度揭示了不同类型混合簇放电的产生机理. 结果表明，当gCAN增加时，混合簇中胞体簇放电的数量会发生变化，同时胞体簇放电类型由“fold/homoclinic”滞后环的“Hopf/homoclinic”型簇放电转迁为“fold/homoclinic”型簇放电，最终胞体簇消失，系统呈树突峰放电模式. 此外，本文还探究了VSERCA增加时，神经元的放电活动由静息态到混合簇放电模式的转迁.

本文的研究表明，pre-BötC兴奋性神经元的放电模式受到VSERCA的间接影响. 混合簇放电的产生不仅在很大程度上取决于INaP和ICAN的共同作用，也受SERCA泵(VSERCA)和钙激活的非特异性阳离子电导(gCAN)的影响. 本文的结果对理解耦合pre-BötC神经元的动力学研究具有重要意义，有助于了解耦合神经元呼吸节律的产生机制，为进一步研究pre-BötC神经元网络的呼吸节律的产生机制提供一些帮助. 此外，本文的研究方法也可以进一步推广到pre-BötC神经元和其他神经元的各种不规则簇放电的动力学研究中.