基于ResNet 与Transformer 的离线手写数学公式识别
周名杰
(南京邮电大学 自动化学院、人工智能学院,江苏 南京 210042)
随着移动设备的快速普及和相关技术的快速发展,更多的输入和识别手写数学表达式的情况出现,这要求我们有快速、稳定和准确的手写数学字符识别方法。但是,手写字符通常风格变化多样,并需要关注上下文信息。除此之外,数学表达式结构复杂,常常为复杂的二维结构,甚至出现多种结构嵌套的情况。不同于在线识别,离线图片中不包含笔迹信息,只能通过图像本身作为单一信息源来识别表达式。因此,对于手写数学表达式的识别研究充满了挑战。
在传统的离线手写数学表达式识别方法中,往往将数学表达式的识别分为两大部分,符号的切分和识别部分以及结构解析部分[1]。字符的切分往往是基于图像中的像素点[2]或者是设计包围字符[3]的包围框等。卷积神经网络方法[4],常被用在字符的识别中。结构解析部分,大致分为两类算法,一类是基于语法的结构解析,如有限从句语法[5],上下文无关语法[6]等。另一类算法是不基于语法的结构解析算法,如MacLean 的贝叶斯模型方法[7],Hirata 的模板匹配方法[8]等。
近年来,基于编码解码结构的方法取得了较为明显的成功。编码解码结构在序列到序列的问题,如自然语言处理任务中拥有不错的表现。ZHANG 的WAP模型[9]中,使用VGG[10]作为编码环节,将输入图片中的特征进行提取,生成序列数据;包含了注意力模块的循环神经网络[11]作为解码环节。密集连接卷积编码器和多尺度注意力模型[12],进一步提升了编码解码结构的性能。
为了解决循环神经网络训练的时序依赖问题,文献[13]提出了完全使用注意力实现的模型Transformer,代替了循环神经网络,在翻译任务上取得了很好的成绩。
针对手写数学表达式识别,本文提出基于ResNet[14]与Transformer 结合的方法,首先通过残差网络,序列化图片中的特征信息,之后经过位置编码[15]添加位置信息。经过处理的特征序列输入到Transformer 进行编码解码计算,达到识别手写数学表达式的目的。
1 方法概述
受编码解码模型以及注意力模型的启发,本文提出一种新型的基于ResNet 与Transformer 网络的结构,用以实现对手写数学表达式的识别工作,整体结构如图1 所示。本模型的输入为单个图像,输出为LaTex 序列的公式表达。

图1 模型整体结构图
整体公式:
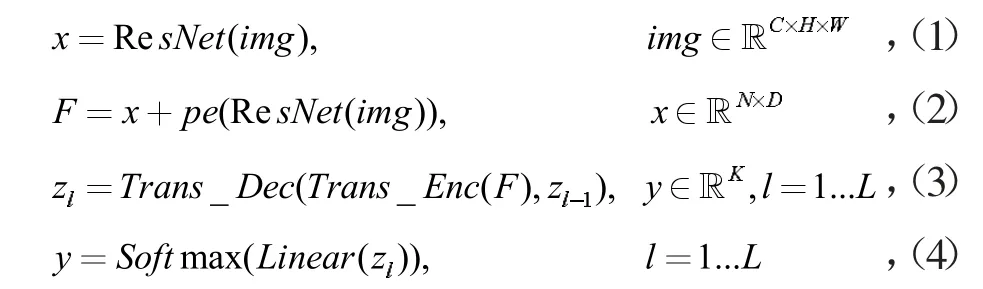
1.1 图像特征提取
1.1.1 残差网络
本文使用的是标准的ResNet34 网络,但是将最后一层全连接层替换为线性网络,实现将C×H×W 的图像转化为N×D 的二维序列。
1.1.2 位置编码
残差网络的输出序列x,以及解码器输出将经由位置编码,用以利用序列之间的位置信息。本文使用的位置编码方式为相对位置编码,并使用三角函数来计算位置信息。公式如下所示:

1.2 编码解码
Transformer 网络中的编码模块由多层子网络组成,子网络包含多头注意力与前向网络。解码模块具有类似的结构,但是增加了掩模多头注意力网络。解码网络的输入是编码网络的输出F、前部分解码网络的输出Zl-1。
1.2.1 多头注意力
多头注意力(图2 右)由多个注意力机制(图2 左)组成,公式为
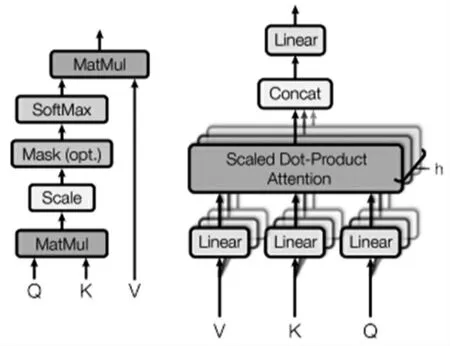
图2 注意力以及多头注意力

1.2.2 掩模多头注意力
解码器在进行对查询、键和值的注意力计算时,需要有一个特殊的当前查询,它需要满足能够包含当前位置以及之前的信息,并且在训练时不会包含“未来的”信息,即当前位置之后的输入。根据注意力模型中softmax 函数的性质,采用负无穷化将当前位置之后的输入,使softmax 计算的结果趋近于0,达到只注意当前以及之前生成结果的目的。
2 训练和预测方法
在训练阶段,目标是最大化预测词的概率,使用交叉熵作为目标函数:
loss=CrossEntropy (y,trg),其中y 是预测标签,trg 是正确标签。
本模型是整体训练的,输入为图片,输出为一维向量,代表各字符所在字典中的序号。字典中包含115 个LaTex 符号以及开始标志
在预测阶段,目标是得到最可能的预测字符向量:
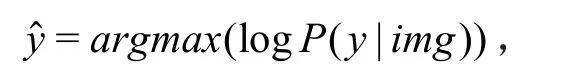
与训练阶段不同的是,我们将过去生成的结果作为假定的正确标签输入,初始输入为开始标志
3 实验
3.1 数据集
我们的数据集使用CROHME2016 的竞赛数据集,数据集共包含8 852 个数学表达式的训练集和1 个包含1 147 个数学表达式的测试集。
3.2 验证
在CROHME 的比赛中,使用表达式正确识别率(竞赛组织者提供)来评价模型的表现。
我们在实验中还使用了单词错误率(WER[16]),每当在表达式中发生替换、删除和增加时,都记作一次错误。其计算公式如下:

3.3 结果及分析
表1 列出了本文方法及其他相关模型在数据集中的表达式正确识别率及WER。

表1 本文方法与其他相关模型对测试数据集中的表达式正确识别对比
与各个参赛的模型进行对比,可以看到本文的方法对测试数据集中的表达式能达到有效识别,单词错误率与WAP 模型相近,证明了本模型的有效性。为了提升表达式正确识别率,我们使用扩展的数据集,扩展数据集除了现有数据之外,还包含了生成数据和采用了随机旋转、缩放和扭曲[17]的现有数据,实验表明表达式正确识别率能够得到提升,达到45.43%,WER 达到18.8%。
与传统的分步公式识别方法进行对比,见表1,尽管Wiris 的公式识别率较高,但是其模型使用了大量的训练数据进行训练,这表明一个好的解析模型对结果的影响很大。
4 结束语
在本文中我们介绍了一种识别手写数学表达式的新方法,它由残差网络与Transformer 网络组成,本模型能有效地在不进行显示分割的情况下完成对字符的识别以及结构的分析,在CROHME2016 数据集上进行了测试。
在未来的工作中,我们计划采用多尺度分析方法来改进模型,以及探索本模型在文本识别等其他场景下的应用。

