基于改进粒子群算法的微能源网优化运行研究

宓禹阳，张自雷

（内蒙古科技大学 信息工程学院，内蒙古 包头 014000）

在环境污染和能源危机的双重压力下，传统的能源利用方式和消费方式已经不能适应社会发展的需要。可再生能源和清洁能源的利用成为了人类社会进一步发展的必然趋势，“能源互联网”和“综合能源系统”等概念应运而生[1]。微能源网作为微型的能源互联网，是能源互联网的末端，其存在尤其可以解决偏远地区或孤立海岛的供能问题[2]。所以，以微能源网为对象的研究越来越受到研究人员的重视。

微能源网最常用的供能方式是冷热电联供技术，运行方式分为孤岛模式和并网模式两种[3]。文献[4]在分时电价及微网并网运行的条件下，以调度周期内系统总运行成本最小为目标函数，建立了一个包含风机、光伏、燃料电池、冷热电联供系统、地源热泵及储能装置在内的微网运行优化模型，采用混合整数规划法对模型求解。文献[5]针对孤岛型微能源网运行特点，引入冷、热、电多类型负荷需求响应，综合考虑能源耦合与转换特性、分布式微源运行特性的基础上，基于能源集线器架构提出了计及多类型需求响应的孤岛型微能源网优化调度模型，采用混合整数规划法求解模型，得出各机组与储能装置的启停状态、最优出力及系统综合运行成本。

目前对微能源网的研究主要集中在优化运行、优化调度和规划等方面[6]。文献[7]提出了基于非合作博弈的冷热电联供微能源网优化的一般模型与求解方法，实现了在兼顾更好消纳可再生能源和用户用能体验情况下的最优经济运行。文献[8]建立了同时考虑离网及并网运行状态的储能配置双层优化模型，采用考虑极值变异的混合型粒子群算法求解，获得了储能装置并、离网状态的协调优化配置方案。文献[9]考虑了微能源网中的不确定因素，如风速、光照和负荷状态等，以全生命周期成本最小和碳排放量最小建立微能源网的多目标随机规划模型，在MATLAB 仿真平台通过NSGAII 算法求取Pareto 前沿，结合多目标优选决策方法确定规划方案。

目前少有面向偏远地区的孤岛型微能源网优化运行研究。本文的研究对象选择一种以风光储直流微电网为基础，附加地源热泵和太阳能热泵来组成的冷热电联供的微能源网，以运行成本最小为目标，采用量子粒子群算法求解优化模型，得出最经济的运行方案。

1 微能源网的结构

本文的微能源网系统如图1 所示，主要包括冷热电联供设备、储能设备和负荷三个部分。其中，冷热电联供设备由风力发电设备、光伏发电设备、地源热泵和太阳能热泵组成，风机、光伏系统供电，地源热泵供冷，太阳能热泵供热。

图1 微能源网结构示意图

2 微能源网的数学模型

2.1 光伏发电的数学模型

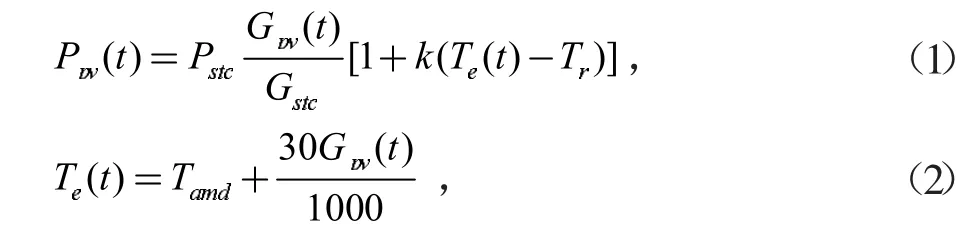
式中，Ppν（t）为t 时段光伏发电机组的输出功率；Pstc、Gstc分别为标准测试条件下光伏电池的输出功率、光照强度；k 为功率温度系数；Tr为参考温度；Te（t）为t 时段光伏电池板的温度；Tamd为外界环境温度；Gpν（t）为t 时段光伏板接收到的光照强度。

2.2 风力发电的数学模型

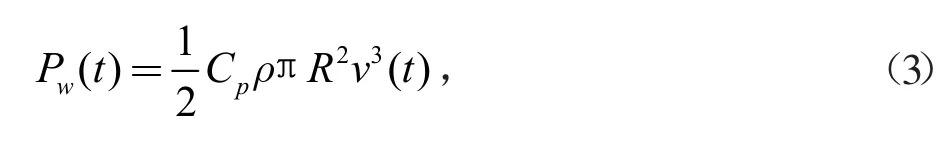
式中，Pw（t）表示t 时段风力发电机组的输出功率；Cp表示风力发电机组的风能利用系数；ρ 表示所在地的空气密度；R 表示风力发电机组的叶片半径；v（t）表示t时段作用于叶片的风速。

2.3 地源热泵的数学模型

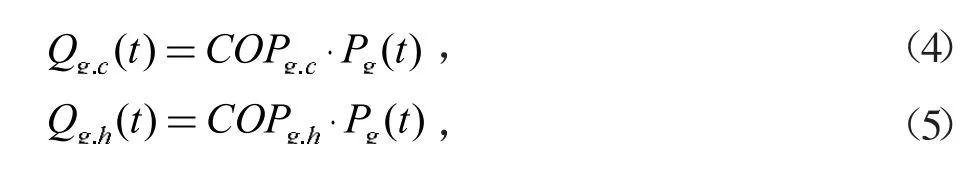
式中：Pg（t）为t 时段地源热泵输入的电功率；Qg.c（t）、Qg.h（t）为t 时段地源热泵输出的制冷功率、制热功率；COPg.c、COPg.h为地源热泵的制冷系数、制热系数。

2.4 太阳能热泵的数学模型

式中：Ps（t）为t 时段太阳能热泵输入的电功率；Qs（t）为t 时段太阳能热泵输出的制热功率；COPs为太阳能热泵的制热系数。

2.5 储能设备的数学模型

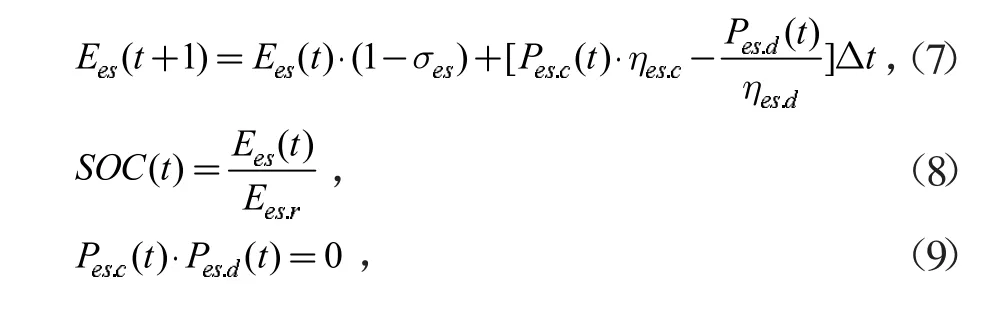
式中：Ees（t）是t 时刻蓄电池的电量；σes是蓄电池的自放电率；Pes.c（t）、Pes.d（t）分别是蓄电池的充放电功率；ηes.c、ηes.d分别为蓄电池充放电效率；SOC（t）是蓄电池的荷电状态；Ees.r是蓄电池的额定电量。

2.6 需求侧响应

可控负荷是需求侧响应的一种重要方式，属于按响应特性分类中的削减负荷，即当能量供应出现不足或剩余时，切除部分负荷或舍弃部分能量，以这样的方式来实现无大电网支撑时系统内能量平衡。因为本文研究的微能源网中的所有设备的输入功率都是电功率，因此可控负荷只需计及电负荷即可。可控负荷实质上等同于一种虚拟微源，通过需求响应成本计入系统的运行成本内，从而可以参与到微能源网的优化运行中。可控负荷的表达式为

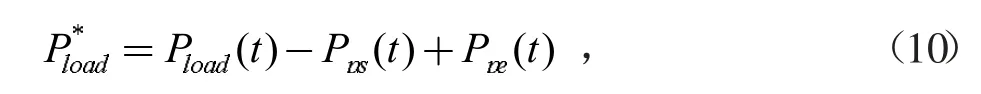
式中，P*load为t 时段计及可控负荷后的负荷；Pload（t）为t时段负荷的预测值；Pps（t）为t 时段能量短缺功率；Ppe（t）为t 时段能量过剩功率。

3 微能源网的日优化模型

3.1 目标函数

该微能源网系统总运行成本包括运行维护成本、设备折旧成本和可控负荷成本。优化的目标是在满足发电需求的基础上，使总成本最少。目标函数的表达式为

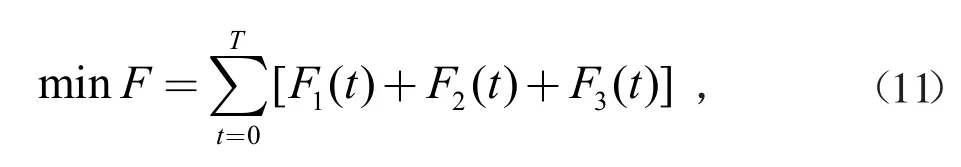
式中，F1（t）、F2（t）为系统在t 时段内的运行维护成本、折旧成本。

3.1.1 运行维护成本

系统的运行维护成本包括风力发电设备、光伏发电设备、储能设备、地源热泵和太阳能热泵的运维成本。表达式如下：

式中，Kom.i、Pi（t）分别表示第i 个设备的单位维护成本、t时段的输出功率。

3.1.2 设备折旧成本

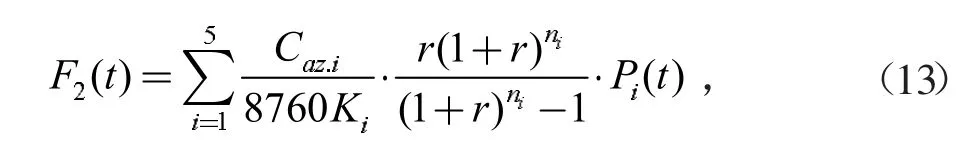
式中，Caz.i为第i 个分布式能源设备单位安装容量成本；Ki为容量因数；r 为折现率；ni为第i 个分布式能源设备的使用寿命。

3.1.3 可控负荷成本

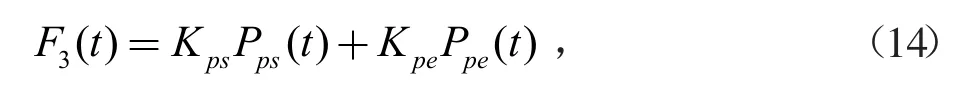
式中，Kps和Kpe分别为电功率能量偏差的单位补偿费用。

3.2 约束条件

3.2.1 能量平衡约束

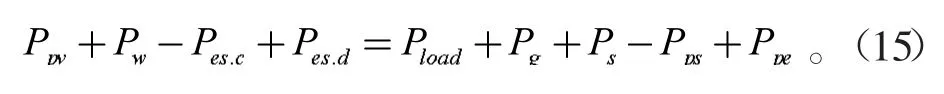
3.2.2 冷热电联供系统出力约束

式中，Ppν.max、Pw.max、Qg.max和Qs.max表示光伏发电机组、风力发电机组、地源热泵和太阳能热泵的最大输出功率。

3.2.3 储能设备约束

式中，Ees.min、Ees.max分别表示储能设备的最小、最大允许容量；Pes.c、Pes.d分别为储能设备最大蓄能、放能功率。

3.2.4 可控负荷约束

式中，Pps.max和Ppe.max分别表示最大短缺功率和最大过剩功率。

3.3 求解方法

微能源网系统中的可再生能源、储能设备和负荷存在能量耦合关系，且优化计算中的优化变量众多，所以该优化问题本质上是多约束、多变量非线性优化问题。状态变量x 是各分布式能源设备的输出功率，其中，储能设备充电时该输出功率为负值，放电时该输出功率为正值。

此类问题一般使用人工智能算法求解。人工智能算法有粒子群算法、神经网络算法、遗传算法、免疫算法和模拟退火算法等，其中粒子群算法具有实现容易、精度高、收敛快等优点，因此便于改进[10]。本文在粒子群算法的基础上，引入轮盘赌算法原理改进粒子群算法来求解优化模型，基于MATLAB 平台编程求解，实现该微能源网的优化运行。

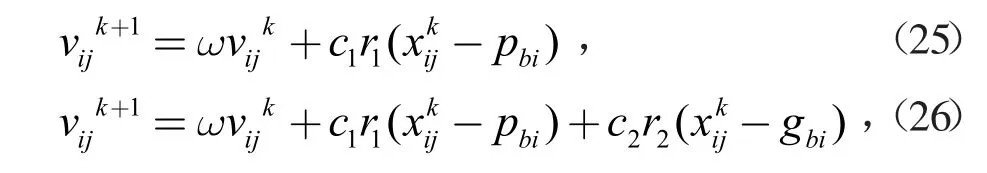
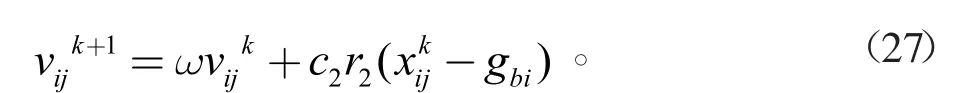
基于以上所述，设置的三种机制：将式（25）设置为机制一，在该搜索机制下，粒子将专注于自身周围的搜索空间，倾向于维持粒子群种群的多样性；将式（26）设置为机制二，在该机制下，全局搜索能力和局部搜索能力达到均衡，有利于粒子跳出局部最优解，避免出现还未收敛到全局最优解就直接终止收敛的情况；将式（27）设置为机制三，在该机制下，粒子将专注于局部开发，有利于提升解的精度。

而轮盘赌原理在该带多搜索机制的粒子群算法中的体现在于：每一个粒子都会有一定的概率选择三个机制之一来更新自身的位置信息，在更新位置的同时会记录下自身近k 次迭代中的变化，还会统计每个搜索机制下的成功率，该成功率会影响下k 代粒子选择相应机制的概率。

该改进算法的流程图如图2 所示。

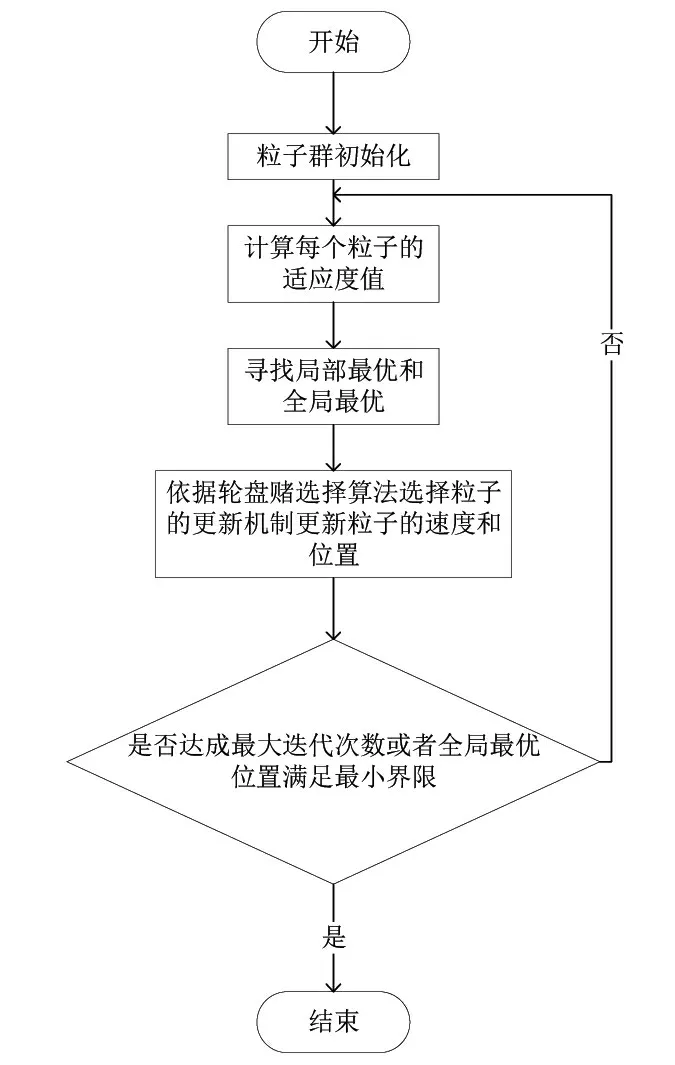
图2 改进粒子群算法流程图

4 算例分析

本文采用的负荷数据取自某偏远地区农户在典型日一天24 小时的负荷预测曲线。各设备的相关参数见表1 至表4。

表1 风力发电设备的参数

表2 光伏发电设备的参数

表3 储能设备的参数

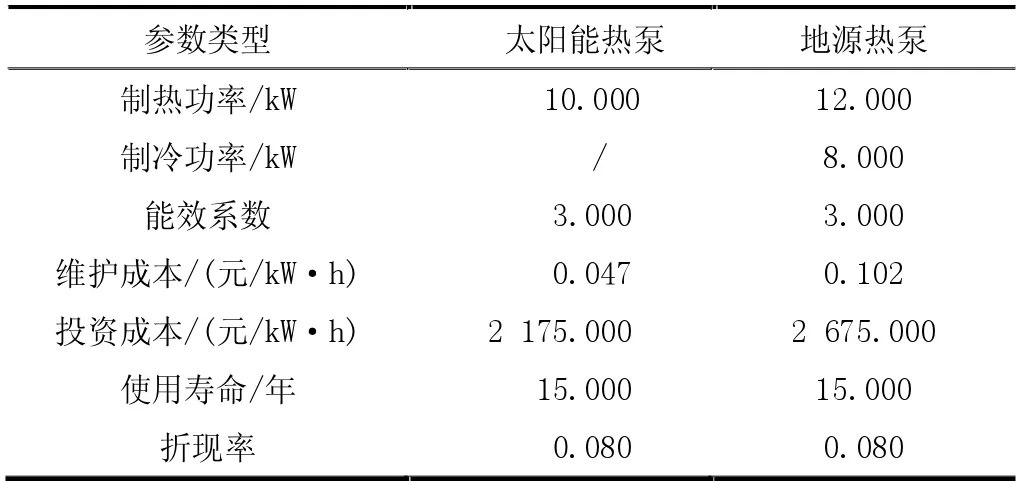
表4 供热供冷设备的参数

典型日的负荷和设备运行曲线如图3 和图4 所示。从图中可以看出，在不考虑供热和供冷消耗的条件下，该居住在偏远地区的用户一天24 小时的用电量是很小的，可以看出明显的用电规律。有3 个用电高峰：6 时、12 时和18 时。其中，6 时至7 时是用户起床、洗漱、做早饭和吃早饭的时间，12 时是用户中午做饭、吃饭的时间，18 时是用户做晚饭吃晚饭的时间。13 时至14 时和21 时至次日5 时，用户进入休息时间，用电量相对偏少。8 时至11 时和14 时至17 时是用户处理各种事务的时间，用电量相对于高峰期少，而多于休息时间的用电量。

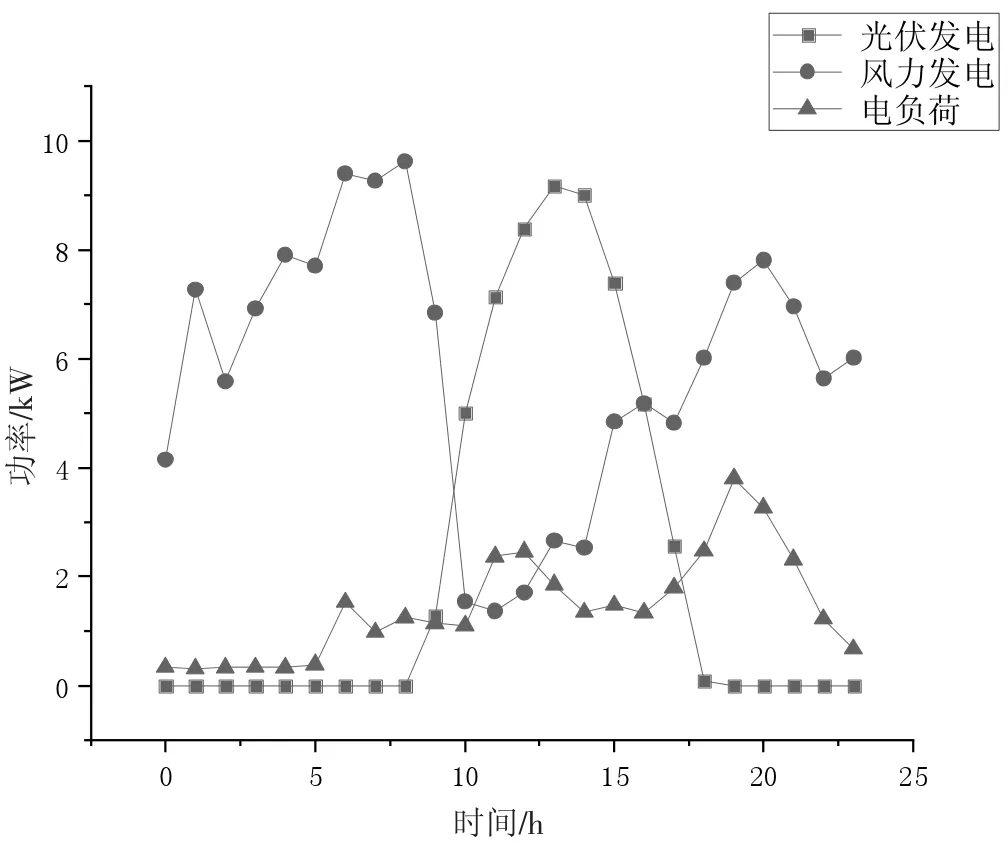
图3 冬季典型日功率预测曲线

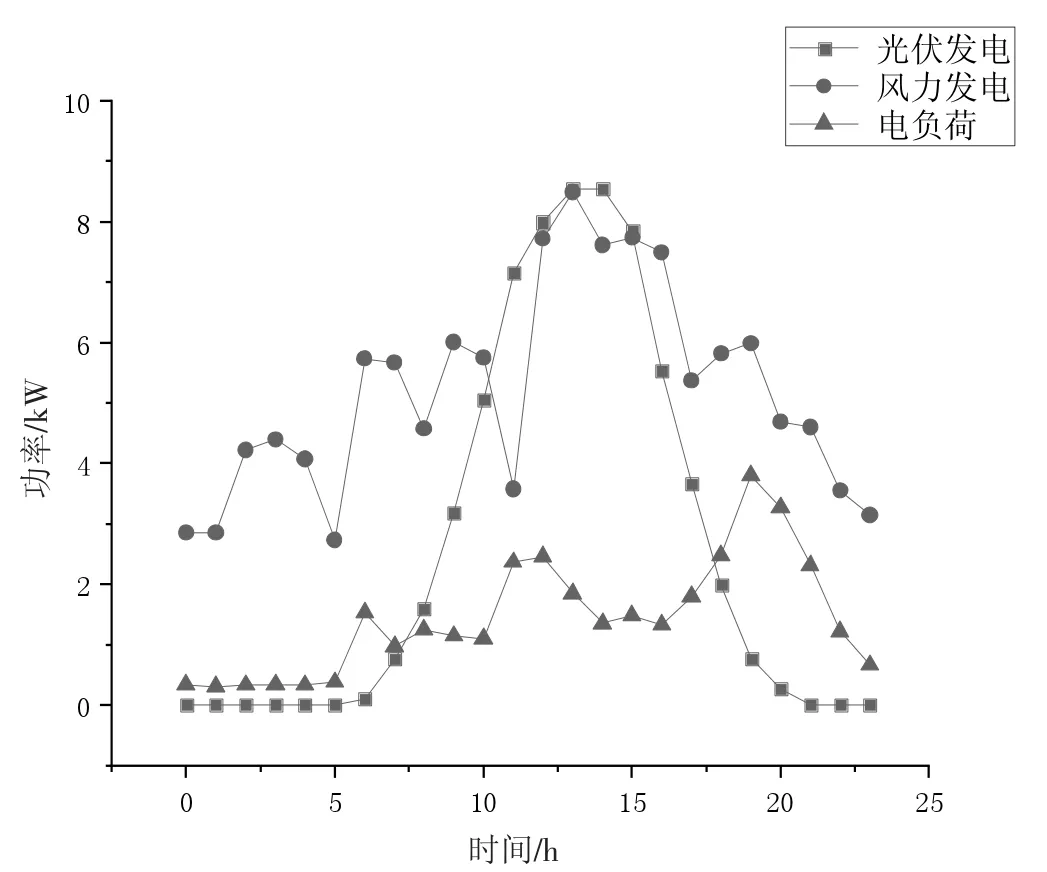
图4 夏季典型日功率预测曲线

根据从该地区采集的气象数据，包括风速、光照强度和温度等得出的风力发电设备和光伏发电设备分别在夏季典型日和冬季典型日的最大出力数据如图3 和图4 所示。

由图5 和图6 可以看出，优化后的能量供需平衡，能够在满足用户用能需求的同时，又能以最经济的方式安全稳定运行。

图5 夏季典型日优化结果

图6 冬季典型日优化结果

冬季典型日电功率优化结果中明显没有完全切除负荷的情况，取而代之的是多采用节约用电的策略。在节约用电的同时，为了保证蓄电池电量在运行周期结束前后的平衡，该改进算法得出的运行策略还会适当的在节约用电时，增加发电量来给蓄电池充电。

夏季典型日中储能蓄电池在该运行方案中，相比于传统粒子群算法得出的方案，让蓄电池实现能量在时间尺度上的转移这一特点发挥得更好。蓄电池分别在11 时、14 时和16 时这3 个时刻释放在其他时刻储存下来的电能，用于供应在经济运行策略调节下能量的缺额，同时也实现了在运行周期前后蓄电池电量不变的约束。

从图中可以看出，在电负荷优化中，由于有可控负荷的存在，避免了经济优化计算后出现的能量不平衡的情况，可见可控负荷发挥了预期的作用，起到了保证孤岛运行模式下微能源网的内部的能量平衡的作用。

那么就可以得出表5 中的结果，由表中的结果可以看出，改进后的粒子群算法计算出的冬季和夏季典型日的运行成本都低于传统粒子群算法，结果说明了改进后的粒子群算法计算结果更小更优，验证了改进算法的可行性和优越性。再结合第四节和本节之前内容的分析，从优化运行策略角度看，改进后的粒子群算法所得出的待优化变量的结果，更能实现蓄电池能量在时间尺度上转移的目的和作用，切除负荷和节约用电的时间段安排更加合乎用户的使用习惯，更具有优越性。

表5 优化计算结果

5 结束语

本文将偏远地区的情况纳入考虑，设计了含有光伏发电设备、储能设备、地源热泵、太阳能热泵的孤岛型微能源网系统，并引入可控负荷辅助控制，保证系统的稳定。在MATLAB 平台上构建日优化运行的模型，输入某居住在偏远地区农户的用能数据和当地典型日的气象数据，基于一种改进权重的混合粒子群算法得出优化结果，体现了模型的合理性。本文模型可以为大电网集中供电难以送达或成本过高的偏远地区的供能问题提供参考，在接下来的工作中，将会把更多可能发生的情况纳入考虑范围，并进一步细化模型，如研究以年为周期的优化运行，或者是考虑光照强度和储能设备剩余能量均不足等极端情况的优化策略。