引导自主探究，深化建模思想——以《17.1.3勾股定理在实际生活中的应用》教学设计为例

◎李幽兰

(武汉市吴家山第二中学，湖北 武汉 430040)

数学源自生活，无处不在，数学在生活中的应用是非常广泛的，很多问题都可以通过构建数学模型巧妙解决这就需要我们学会用数学的眼光看待生活中的事物，引导和鼓励学生构建适当的数学模型，用所学的数学知识分析问题和解决问题，培养学生观察、分析、思考、总结、协作的能力，让学生体会数学知识的奇妙和学以致用的成就感勾股定理是数学中的一个重要定理，它是古代数学智慧的结晶，是用代数思想解决几何问题的杰出代表下面以勾股定理在实际生活中的应用这一课的教学设计为例，探讨构建数学模型在高效课堂中的应用

一、内容和内容解析

1内容：利用勾股定理进行简单的计算，解决生活中的实际问题

2内容解析：勾股定理是最基本的数学定理之一，体现了直角三角形中三条边之间的数量关系，它可用于解决直角三角形中的计算问题勾股定理在实际生活中具有广泛的用途，本节通过联系、比较、探索、归纳，帮助学生理解勾股定理，通过独立思考与小组活动培养学生的分析能力和探究能力，以利于学生能够正确地运用勾股定理解决实际问题

二、目标和目标解析

1目标：

(一)知识与技能：学生能说出勾股定理,能运用勾股定理的数学模型解决实际问题

(二)过程与方法：①通过从实际问题中抽象出直角三角形这一模型，深化“数形结合”和“转化”的数学思想，将非直角三角形转化为直角三角形，立体图形转化为平面图形；②经历探究勾股定理的应用过程，培养学生数学建模的意识，提高学生解决问题的能力；③运用分类讨论的思想，让学生更加全面地思考问题

(三)情感态度与价值观：①数学源于生活，让学生体会勾股定理在实际生活中的运用；②让学生自主探索，团结协作，发挥学生的主观能动性，培养学生不怕困难，积极自信的心理素质和思想品质；③让学生热爱校园，保护环境，加强环保意识和道德意识

2目标解析：

达成目标(一)的标志是：学生能够运用勾股定理解决实际问题

达成目标(二)的标志是：学生知道怎样将实际问题转化为直角三角形模型

达成目标(三)的标志是：学生积极参与课堂学习，对数学学科的学习充满信心和兴趣

三、学情分析

在利用勾股定理探索实际问题的过程中，老师要让学生经过思考克服困难，通过小组协作的形式实现高效课堂，提高学生的积极性和参与度，提高教学效率和教学效果让学生在一堂课上不但收获数学知识，还能从能力上、情感上、道德品质上都有收获，促使每个学生都能得到相应的发展

本节课的教学重点：运用勾股定理解决实际问题

四、教学过程设计

(一)创设情境，导入新课

教师引言：数学源于生活，也服务于生活大家一起来看看这个问题能否用数学知识解决？

问题：如图，学校有一块长方形的花坛，有些同学为了走捷径，就在花坛内的草坪上走出了一条“小路”，请你算一算，他们仅仅少走了________步路，却踩坏了草坪(假设两步为1米)

图1

师生活动：让学生回顾勾股定理的内容，并尝试运用勾股定理解决这个问题教师在学生回答的基础上明确提出解决问题的方法：同时指出这种方法就是构建直角三角形勾股定理的数学模型，将实际问题转化为数学问题，从而运用勾股定理解决

根据勾股定理,

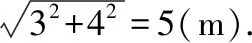
2×(3+4-5)=4(步)

因此,有的同学仅仅少走了4步路，却踩坏了草坪

【设计意图】让学生回忆勾股定理的内容，并注意文字语言、图形语言、符号语言的规范，初步体会通过建立数学模型解决实际问题,同时渗透 “两点之间，线段最短”，为后续教学内容做铺垫，也让学生明白数学的价值不仅在于方便生活，更让我们看清事物的本质，坚守道德与正义，呼吁大家要爱护校园环境

(二)新知构建，共研释疑

1木板通过问题

1(人教版八年级数学下册教材第25页例1)一个门框的尺寸如图所示,一块长3 m，宽22 m的长方形薄木板能否从门框内通过？为什么?

图2

1木板横着能否通过？

2木板竖着能否通过？

3在长方形中，,,哪条线段最长？

4门框能通过薄木板的最大宽度是多少?

学生带着问题进行小组讨论，通过小组组员协作演示，展示解题过程并讲解，同时组员补充老师对学生的解题思路予以正面评价，但是关于运用勾股定理的书写过程，老师要进行格式上的规范和强调

如图所示，在Rt△中，根据勾股定理,

图3

得=+=1+2=5，

所以木板可以从门框内通过

【设计意图】让学生能从实际生活的角度大胆考虑，用生活经验和学过的数学知识加以思考和分析，最后能够顺其自然地想到将木板斜着通过门框，从而将这个实际问题转化为解直角三角形的问题，成功构建了数学模型

2梯子滑动问题

2(人教版八年级数学下册教材第25页例1)如图所示，一架26 m长的梯子斜靠在一竖直的墙上，这时为24 m如果梯子的顶端沿墙下滑05 m,那么梯子底端也外移05 m吗?

分析问题:此题首先要计算梯子底端外移多少米，可以转化为求的长度，而=-，自然想到要先利用勾股定理求、的长，老师引导学生完成这道题目然后用电子展台将学生的解题过程展示出来，并给予正面评价，再次强调运用勾股定理的书面格式要规范

图4

在Rt△中，根据勾股定理,

得=-=26-24=1，

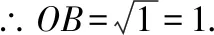
在Rt△中，根据勾股定理,

得=-=26-(24-05)=315

∴=-≈177-1=077

所以梯子的顶端沿墙下滑05 m时，梯子底端并不是外移05 m，而是外移约077 m

【设计意图】引导学生建立数学模型，分别画出相应的直角三角形，明确已知量和所求量，再分析和转化，提高学生分析问题、解决问题的能力

1一种盛饮料的圆柱形杯(如图)，测得内部底面半径为25 cm,高为12 cm,吸管放进杯里，杯口外面至少要露出46 cm，求吸管至少要做多长

图5

学生独立思考完成变式练习，然后小组成员对各自的答案汇总和讨论，由小组代表上台充当小老师讲题，其他小组成员可以对讲解不清的地方发起提问，最后老师评价和补充

【设计意图】巩固训练学生运用勾股定理在建立数学模型中解决问题的能力，培养学生自主探究、小组合作的学习能力，学习他人的长处，发现自己的不足，同时也站在教师的角度看待问题，更加全面和客观地评价事物

(三)巩固训练，迁移拓展

3表面距离最短路径问题

3如图，一只蚂蚁在棱长为的正方体表面爬行，它从顶点爬到顶点去寻找食物,则它走过的最短路程为( )

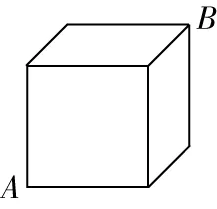
图6

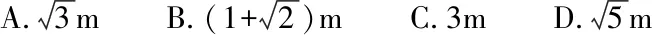
教师引导学生完成例题，总结解题方法

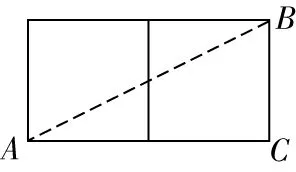
图7

【设计意图】对于平面图形，由“两点之间，线段最短”可以直接运用勾股定理求出两点之间的距离，将立体图形的侧面展开，转化为平面图形，构造直角三角形，才能将实际问题转化成可以用勾股定理计算的问题通过例题分析，建立数学模型，有利于帮助学生把握解题思路和技巧，促使学生学会归纳与总结方法

2有一个圆柱,它的底面半径为3 cm,高为12 cm，在圆柱的底面点有一只蜗牛,它想从点爬到点,请问这只蜗牛沿着圆柱侧面至少要爬行多少厘米

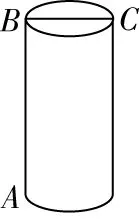
图8

3长方体盒长、宽、高分别为5 cm,3 cm和8 cm,在盒子底端点有一只小虫子，它想从盒子表面点爬行到点，那么小虫子爬行的最短路程为________cm

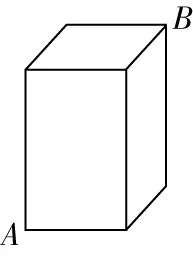
图9

师生活动：将学生小组分成两部分，一部分做变式练习2，一部分做变式练习3，学生根据例题的方法，独立思考完成变式练习，然后小组成员之间讨论答案，以小组为单位展示解题过程(包含展开图)并讲解题目，进行小组比拼，然后老师点评和补充，同时提醒学生注意变式2只有一种情形，而变式3需要分类讨论，考虑三种不同的展开图情况，再来比较哪种路径最短，并比较两个变式练习与例3的联系与区别对于小组比拼中表现优秀的学生和小组进行加分和全班鼓掌鼓励，让班级形成良性的竞争氛围

【设计意图】巩固训练学生解决立体图形求表面最短距离的问题，讨论答案和学生讲解的过程让学生在输出的同时看到自己的不足，同时可以体会获得成功的喜悦通过具体问题，深化运用勾股定理解决问题，通过学生的讲题和小组之间的比拼，形成良性竞争，激发学生的集体荣誉感和比赛积极性

(四)课堂总结，反思升华

首先学生自由发言，表达自己本节课的收获，然后教师概括并加以补充和升华

一节课的成功在于，教学目标明确，教学过程合理，学生积极参与、收获知识并提高能力本节课的教学设计紧紧围绕着构建直角三角形的勾股定理解决数学模型问题，以及怎样构建数学模型，让学生感受数学的生活气息，激发学生学习数学的积极性本节课每个环节都充分体现了学生的主体地位，引导学生主动“自找水源”的学习意识；通过创设生活化情景，贴近学生的生活，达到最近发展区，深化数学建模思想；通过小组的组员之间、组与组之间、师生之间的课堂活动，形成互帮互助互补的师生学习共同体，更有利于形成良好的学习氛围和学习习惯