偏载工况下带式输送机输送带跑偏及纠偏研究*

余 浩,田俊杰,姚 庆,刘红梅,2*

(1.南通大学 机械工程学院,江苏 南通 226019;2.南通大学 交通与土木工程学院,江苏 南通 226019)

0 引 言

带式输送机是一种广泛应用于散料输送的设备。它是由输送带、主驱动辊、从动辊、托辊、张紧装置、驱动电机等组成的复杂机电系统。其中,输送带是整个系统中重要组成部分,起着承载和牵引的作用[1]。

目前,带式输送机正朝着长距离、高速度、大运量方向发展。这对其传动系统动态稳定性的要求不断提高,对输送带跑偏问题研究也成为了热点[2]。

输送带跑偏的原因有很多,例如,机架生产或安装的精度过低、托辊中心线不平行、张紧装置安装存在偏差,以及物料偏载等因素均会引起输送带的跑偏。

在通常情况下,输送带的跑偏主要是由物料偏载引起的。在散料运输过程中,由于生产的需要和空间的限制,输送线上需要设置专门的转载结构,以对物料进行转载,但常会因为转载而造成输送带受料不居中,导致后段输送带出现跑偏现象。

目前,针对输送带跑偏问题,国外学者已进行了大量研究。

SIEVERS L A等人[3]将输送带当作铁木辛柯梁,对多段输送带组成的系统进行了跑偏趋势分析。HAN Feng-lin等人[4]基于环状平带本身内部机械反馈,分析了侧向抗弯刚度数值较小的输送带在系统中的跑偏规律。NGUYEN V等人[5]为了提高带式输送机系统的稳定性,基于带式输送机模型和模糊控制的自适应控制算法,对其参数进行了分析和控制,并评价了各参数对带式输送机跑偏的影响。

国内学者也针对输送带跑偏问题进行了大量研究。

师建国[6]分析了输送带产生侧向跑偏的激励源,构造出了输送带侧向运动非线性动力学连续模型,并结合输送带实际工况,得到了输送带侧向运动的动力学方程。张志亮[7]对输送带的跑偏问题进行了研究,提出了一种经过改进的输送带自动纠偏装置。贺晋璇等人[8]分析了调心托辊水平偏转角对输送带纠偏能力的影响,并据此建立了相关输送带纠偏平台。黄卓等人[9]采用ABAQUS仿真的方法,得到了输送带的运动规律,研究了其在建模、分析与后处理过程中的主要问题,以及其相应的处理办法。针对输送带受料跑偏问题,方建新[10]对输送带移动线、进入点及进入角之间的联系进行了研究,从运动学的角度,对于因进入角大小改变而引起输送带的跑偏的各类因素进行了分析。针对输送带跑前不跑后、跑松不跑紧的规律,许之朋[11]对滚筒安装误差和托辊安装误差引起输送带跑偏进行了受力分析,并分析了物料落点不正引起的输送带跑偏。

综上所述,针对带式输送机仿真主要集中于动力学仿真研究,并且研究的关注点在于输送带的运动方向及纠偏方法,而对输送带受料偏载和物料冲击方面的研究则较少。并且,上述研究中对于物料颗粒的仿真也主要集中在离散元仿真软件EDEM的应用上。

因此,笔者采用EDEM软件与ADAMS软件耦合仿真,针对物料偏载工况下输送带跑偏问题进行动力学研究,并进行纠偏试验仿真。

1 理论分析

根据引言中的描述,在散料运输过程中,由于生产的需要和空间的限制,输送线上需要设置专门的转载结构,以对物料进行转载。

输送带的转载结构如图1所示。

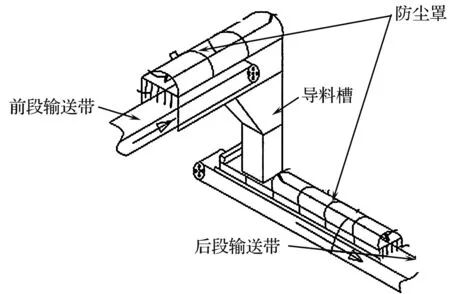
图1 输送带的转载结构

对带式输送机的运行主要需要关注两点,即输送带与偏载受料。

笔者针对输送带采用刚体有限元法将输送带分割成小带块,并在ADAMS软件中运用轴套力进行连接,形成柔性带;采用EDEM软件模拟生成物料,与输送带接触碰撞产生作用力,观测其对输送带跑偏的影响。

1.1 输送带离散模型及方程

刚体有限元法是一种基于融合多刚体动力学理论与离散方法而形成的柔性动力学分析方法,其思想是将柔性或者刚柔混合系统离散为具有质量、惯性刚体单元(rigid finite element),刚体单元之间的连接依靠弹簧阻尼单元(spring-damping elements)[12-13]。

笔者采用刚体有限元法是将输送带离散为多个小刚体单元块,应用弹簧阻尼单元将各个小刚体单元块连接起来,其刚度特性由刚体单元描述,柔性特性则通过弹簧阻尼单元来体现。

输送带离散单元模型图如图2所示。

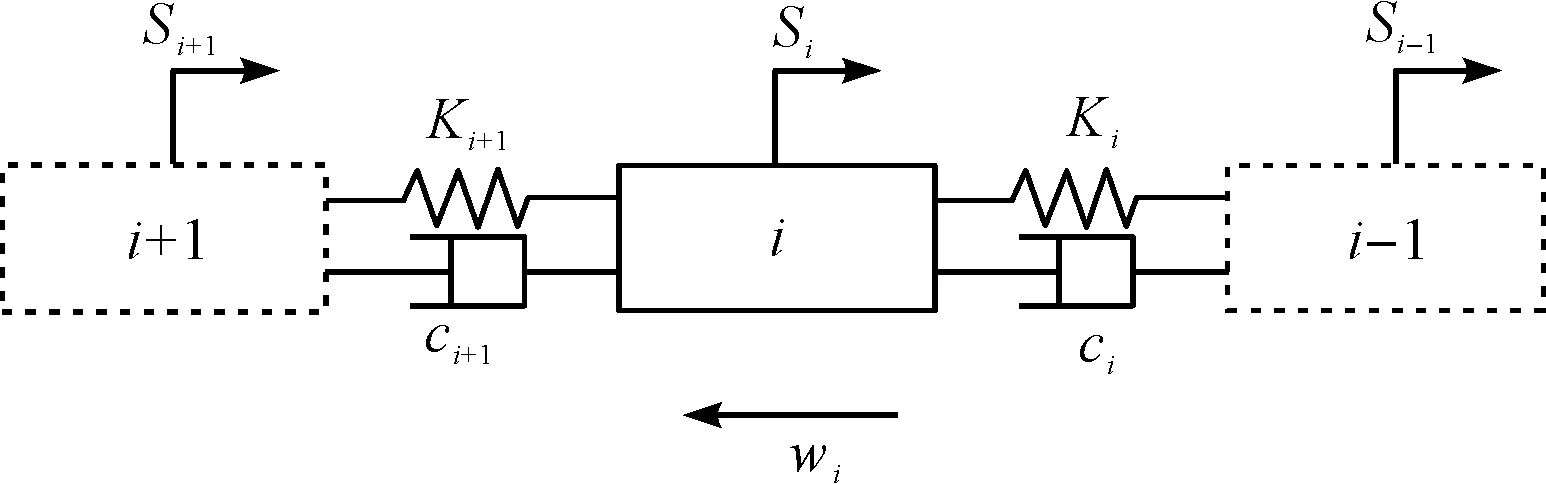
图2 输送带离散单元模型Ki—单元i-1与i间刚度;ci—单元i-1与i间阻尼;Ki+1—单元i与i+1间刚度;ci+1—单元i与i+1间阻尼;mi—单元i质量;wi—运行阻力;Si—单元i运行位移

图2中,相邻刚体单元之间用轴套力连接;输送带被切割为多个单元,单元i上有刚度和阻尼,分别为Ki、Ki+1、ci、ci+1;在质量为mi,运行阻力wi的作用下,若其位移为Si,则单元i的动力学方程为:

(1)

笔者将输送带做以下离散化假设:

(1)输送带垂度变化引起输送带长度变化较小,可忽略不计;

(2)带式输送机的驱动辊、从动辊固定,输送带视作两端固定的纵向梁;

(3)输送带及物料密度沿纵向(输送带运行方向)均匀分布;

(4)托辊密度沿输送带运行垂直方向均匀分布;

(5)输送带力学特性遵循各向同性,且变形处于线弹性变形范围之内。

1.2 输送带连接及计算方程

在ADAMS软件中,输送带轴套力的连接如图3所示。

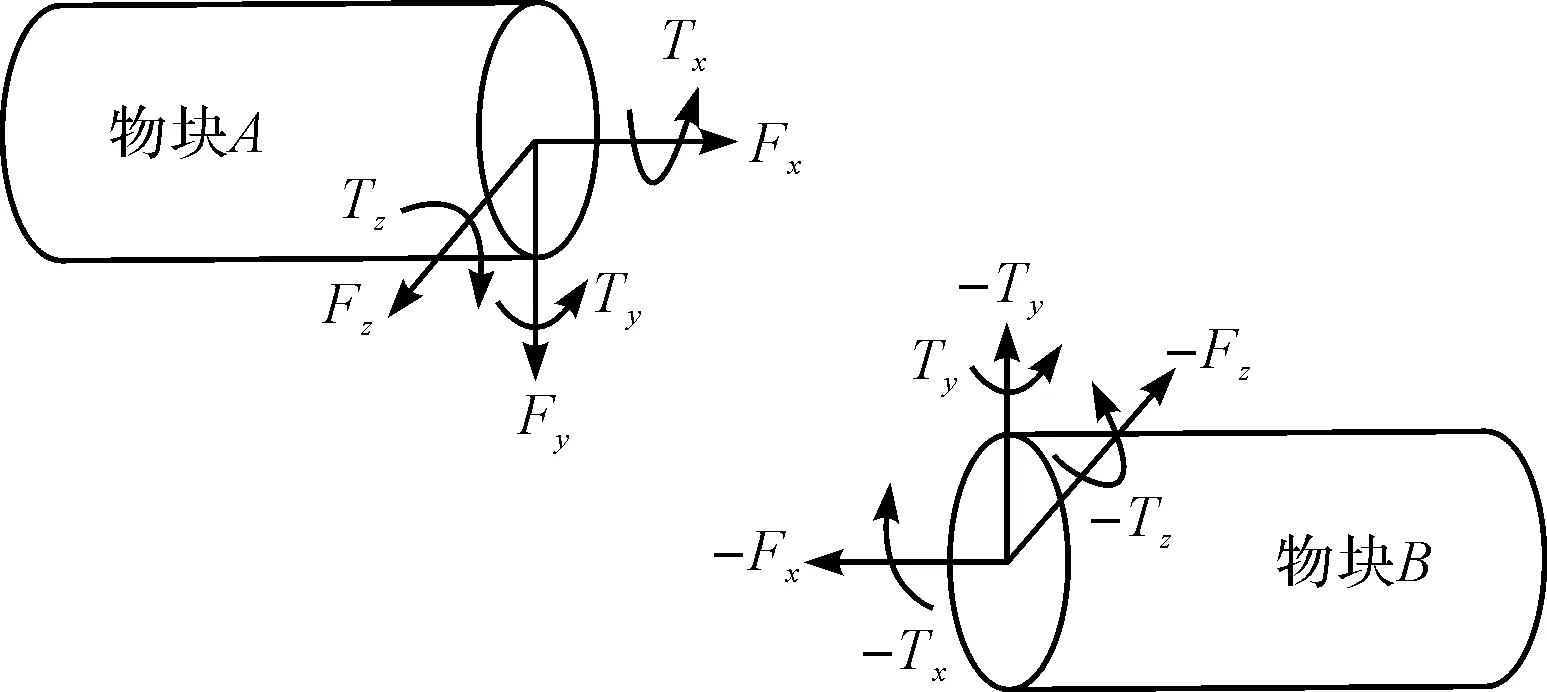
图3 输送带轴套力连接

在图3中,轴套力包括6部分,即由x、y、z三坐标轴张力和各坐标轴旋转力矩组成,分别为Fx、Fy、Fz、Tx、Ty、Tz。

其中,Fx参数定义如下[14]:

Fx=K11Rx-c11Vx+Fx0

(2)

式中:K11—刚性系数;Rx—两刚体单元x方向位移,mm;c11—阻尼系数;Vx—两刚体单元x方向速度,mm/s;Fx0—刚体间预紧力,N。

同理,可得Fy、Fz、Tx、Ty、Tz表达式,其通过矩阵形式的表达式为:

(3)

输送带刚度矩阵、阻尼矩阵的计算式如下:

(4)

(5)

式中:K11—拉伸刚性因子;K22,K33—剪切刚性因子;K44—扭转刚性因子;K55,K66—弯曲刚性因子;c11—拉伸阻尼因子;c22,c33—剪切阻尼因子;c44—扭转阻尼因子;c55,c66—弯曲阻尼因子;E—弹性模量,N/mm2;G—剪切模量;A—带块横截面积;η—材料剪切黏性系数;χ—截面形状系数,取1.2;b,h—刚体单元带块宽度和厚度,mm;β—与h/b有关系数;I2,I3—输送带对横截面形心轴的惯性矩。

2 输送机模型及参数设置

2.1 输送带模型及参数设置

笔者在SolidWorks软件中,建立简化的带式输送机三维模型,并生成.xt文件,将其导入ADAMS中;再对导入后的模型施加运动副、接触、驱动等,最终搭建完成输送机模型,如图4所示。

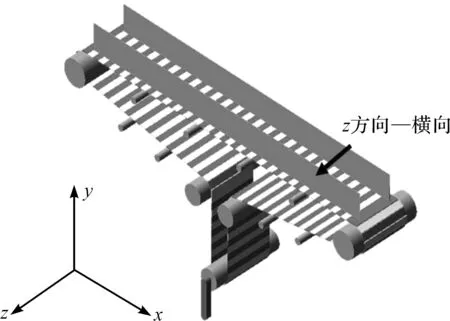
图4 带式输送机模型

在图4模型中,x轴正向水平向右,y轴正向水平向上,z轴正向垂直于纸面向外,坐标系符合右手定则,输送带z方向为横向。

此处带式输送机的主动辊和从动辊直径为400 mm,首尾间距5 000 mm,托辊直径100 mm,张紧辊和转向辊直径为300 mm,长度均为1 200 mm,输送带带宽800 mm,带块厚10 mm;

通过查阅相关文献[15-17]与前期的仿真实验结果,笔者设置带块长度Δl与主动辊的比值为0.06～0.27,设置其与张紧辊的比值为0.08～0.33;在确保仿真准确和高效的前提下,设置带块长Δl为100 mm。

根据输送带材料计算输送带刚度与阻尼,笔者建立轴套力连接输送带带块。

输送带材料参数如表1所示。

表1 输送带材料参数

依据式(4,5),可得到输送带刚度矩阵与阻尼矩阵,即:

K=

式中:K—刚度矩阵;c—阻尼矩阵。

2.2 颗粒模型及参数设置

此处,笔者针对某建筑固废企业生产线上带式输送机输送带(物料以石、砂混合物为主,粒径为60 mm)出现跑偏问题进行具体研究。

该输送机运输量45 kg/s,输送带带宽为800 mm,带速为1.5 m/s。在运输过程中,颗粒与颗粒碰撞,颗粒与挡板碰撞及颗粒与输送带碰撞,接触模型设置为Hert-Mindlin(no slip)。

颗粒模型如图5所示。

图5 颗粒模型

颗粒与材料属性如表2所示。

表2 颗粒与材料属性

接触参数设置如表3所示。

表3 接触参数设置

2.3 ADAMS-EDEM耦合原理及参数设置

EDEM能够模拟颗粒与颗粒及颗粒与几何体碰撞运动过程及能量传递过程,但是其导入的几何体只能实现平动、转动及简单的复合运动。

ADAMS软件适用于动力学仿真运算,其能够实现复杂的运动,但是对于其受到复杂载荷力,需要进行外部数据的导入。

因此,结合两者的优点,能够实现连续载荷冲击下输送带的持续运动。ADAMS与EDEM的耦合是通过Co-simulation实现的。

ADAMS与EDEM耦合原理如图6所示。

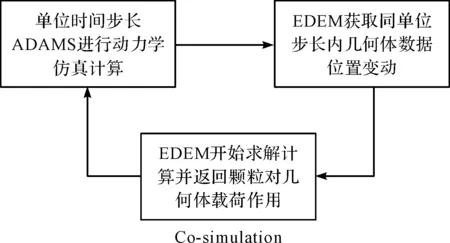
图6 ADAMS与EDEM耦合原理

由图6可知:在单位时间仿真步长内,通过Co-simulation将ADAMS中输送带运动参数信息导入EDEM中,EDEM将输送带接受物料载荷信息传递给ADAMS中;ADAMS根据传回载荷信息及自身驱动信息计算出新位移、新速度,完成数据的循环传递过程,直到耦合仿真结束。

其中,需注意ADAMS仿真时间步长设置为EDEM仿真时间步长的整数倍,总仿真时间为15 s,步长设置为0.05 s。

3 输送带仿真及结果分析

笔者对输送带进行两种状态(空载与偏载工况)仿真,分析偏载工况下输送带跑偏问题,并进行纠偏。

3.1 输送带空载下仿真分析

笔者对带式输送机进行空载工况下运行仿真分析。

输送带横向位置如图7所示。

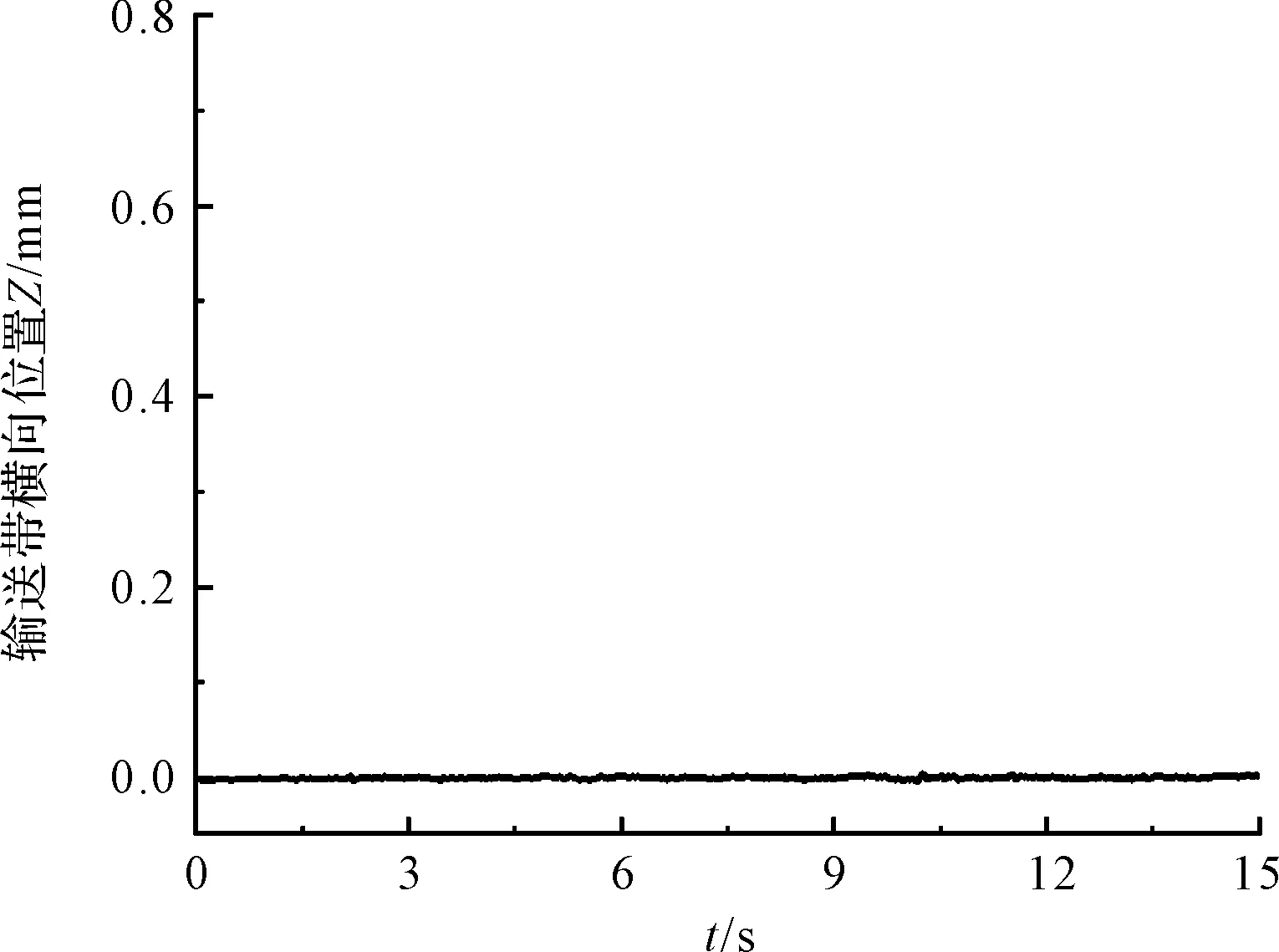
图7 空载工况下输送带横向位置

由图7可知:输送带在无负载时,由于主动辊的牵引,在托辊处会产生小幅横向振动,但是输送带整体横向位置趋近于0 mm,说明输送带在无负载时不会出现跑偏现象。

可见,在ADAMS中建立的带式输送机模型是正确的,符合实际工况。

3.2 输送带偏载下仿真分析

笔者对带式输送机进行偏载工况仿真,以输送带带块1的位置显示其在承载段的运行方位,带块1在落料位置如图8所示。

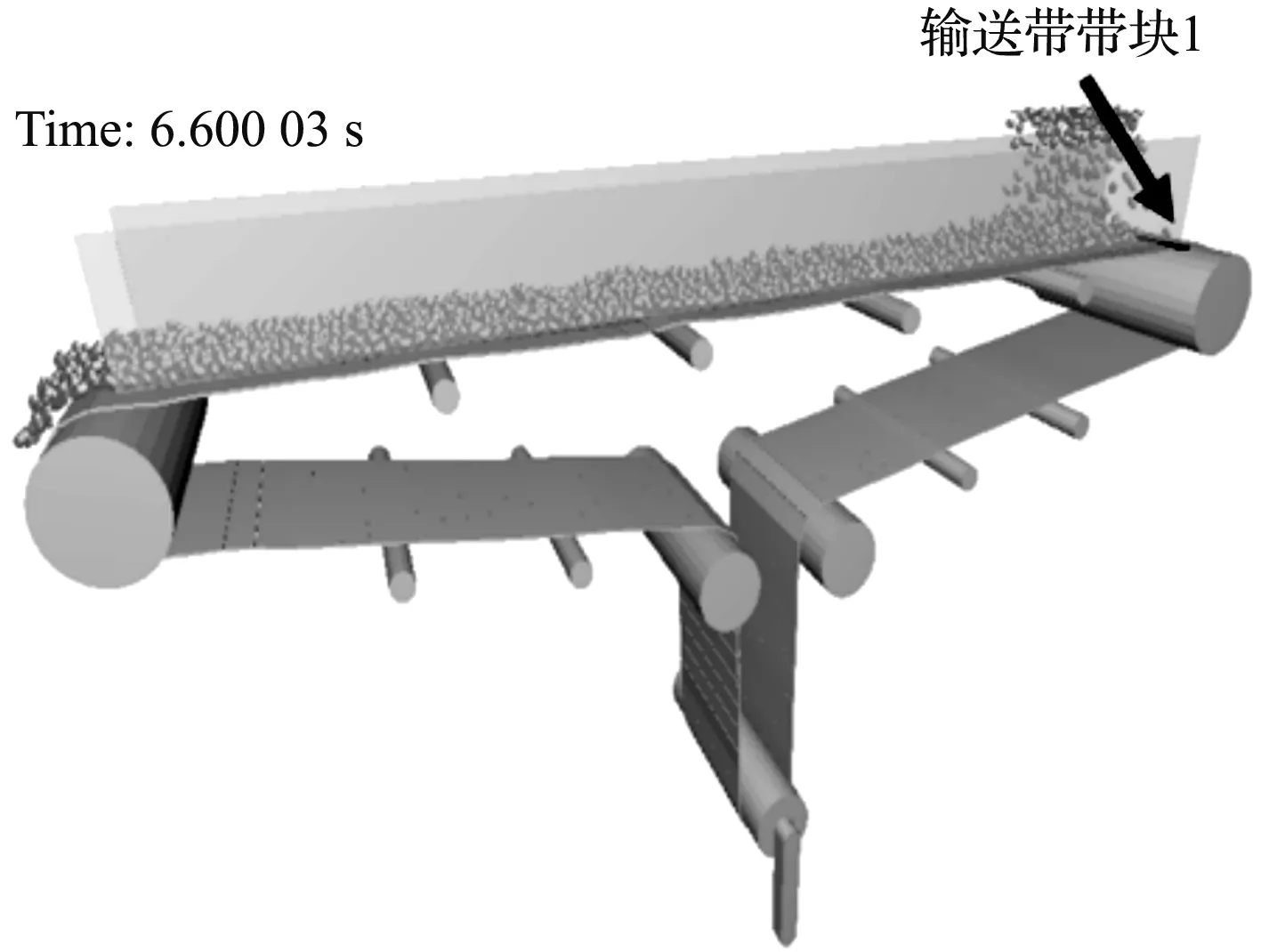
图8 输送带带块1在落料位置

输送带带块1在卸料位置如图9所示。

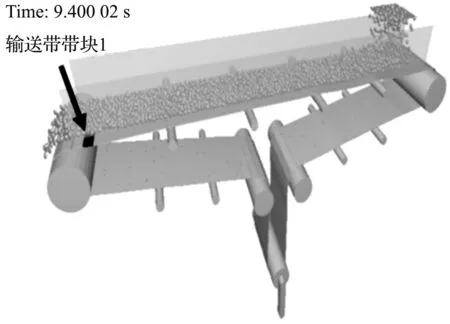
图9 输送带带块1在卸料位置

由图(8,9)可知:在6.6 s～9.4 s时,输送带带块1在承载段运行,输送带带块1在落料位置时(对应时刻6.6 s),所受外部激励较大,导致输送带块横向振幅变大,从而引起输送带横向不稳定,引起更大跑偏趋势。故需要对输送带落料点位置设置缓冲装置。

无缓冲装置时,偏载落料下输送带横向位置如图10所示。

图10 偏载落料下输送带横向位置

由图(9,10)可知:输送带带块在离开主驱动辊完成卸料(对应时刻9.4 s)后会产生横向跑偏趋势,落料与卸料时间段内输送带横向振动幅度较大。

因此,需在输送带主驱动辊下方加装纠偏装置,以降低输送带横向跑偏趋势[18]。

3.3 缓冲与纠偏仿真分析

3.3.1 缓冲分析

由于前文已分析输送带产生横向跑偏外部激励位置,此处笔者设置缓冲装置与纠偏装置。其中,缓冲装置设计如图11所示。

图11 缓冲装置结构图

在ADAMS中缓冲装置结构的简化模型如图12所示。

图12 ADAMS中缓冲装置简化图

图12中,输送带受料缓冲装置组成部分有机架、托辊、弹簧及底座。

在偏载工况下,笔者对是否安装缓冲装置的输送带横向位置进行仿真分析。

输送带带块横向振幅如图13所示。

图13 有无缓冲装置下偏载下输送带横向位置

由图13可知:在受到偏载落料时,无缓冲装置下,输送带受到横向冲击较大;而有缓冲装置时输送带受到横向冲击减小,在有缓冲装置下输送带带块在6.3 s到9.4 s时的横向冲击幅值也降低了,输送带横向跑偏值减小。

3.3.2 纠偏分析

输送带纠偏装置结构设计图,如图14所示。

图14 纠偏装置结构图

图14中,纠偏装置组成部分有机架、阻挡板、托辊、弹簧及电机。

ADAMS中的纠偏装置简化图如图15所示。

图15 ADAMS中纠偏装置简化图

由于带式输送机GB/T 10595—2017中规定输送带跑偏量不得超过带宽5%,则800 mm带宽输送带跑偏值不得超过40 mm,故笔者在此处采用35 mm作为限位值,对其进行监控;在弹簧处设置位置传感器,此处选用K=10 000 N/m,c=160 N·S/m,当输送带与纠偏辊一侧接触时,弹簧受力开始位移,当位移达到输送带限位值时,纠偏辊开始复位,将输送带复位到中间0 mm处。

纠偏过程中,输送带横向位置的仿真数据如图16所示。

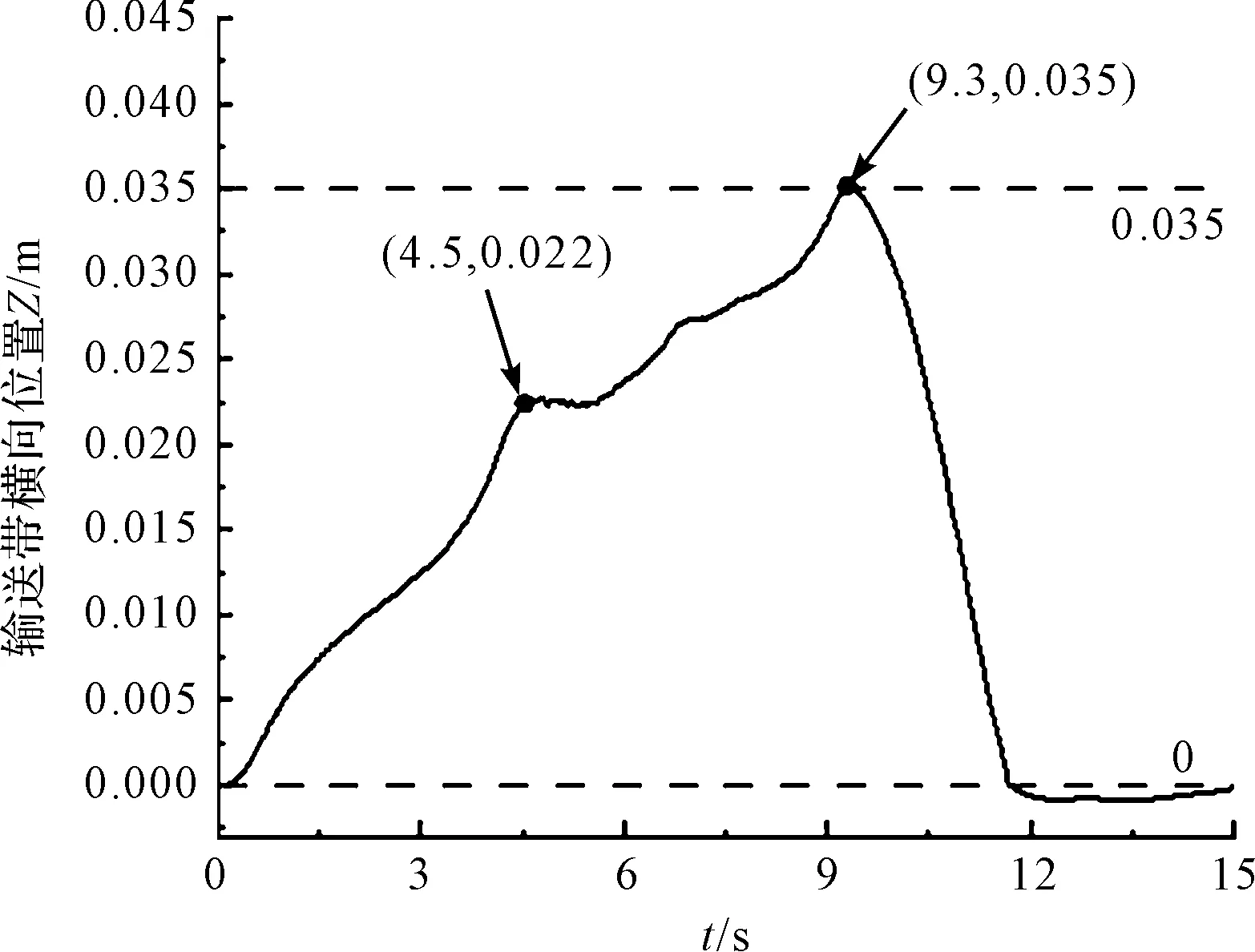
图16 纠偏过程中输送带横向位置

从图16可知:输送带在受到横向力后开始跑偏,输送带在4.5 s时接触到阻挡板及弹簧后受到阻力跑偏逐渐减缓,位置传感器一直处于监控状态;当输送带9.3 s时跑偏值达到35 mm,纠偏辊进行复位运动,最终输送带回位到0 mm附近[19]。

4 纠偏平台搭建及试验

为了对输送带纠偏装置仿真模型的可行性进行验证,笔者搭建了纠偏试验平台。

笔者预先对纠偏装置进行简化。简化后的纠偏装置的组成部分为:压力传感器及配套的放大器、PLC控制器及定位器、PLC模数转换模块、步进电机及配套步进驱动器、线性模组及其他配件。

纠偏装置试验平台如图17所示。

图17 纠偏装置平台1—压力传感器与放大器;2—导轨;3—模数转换器;4—PLC;5—激光笔;6—电阻7—电源;8—步进驱动器;9—数据传输线;10—笔记本;11—联轴器;12—步进电机

笔者对PLC进行控制程序设计,程序设计包括对传感器数据读取与比较,根据比较结果分析输送带是否居中。

在纠偏实验中,前期需要进行多个限位点设置,以验证纠偏理论与纠偏方法的准确性与合理性。由于在平台上频繁进行弹簧更换不方便,也容易对平台造成损坏,导致测量误差的产生;同时,压力传感器测量输送带所受横向力比计算弹簧形变力更方便、准确,此处笔者采用压力传感器来替代弹簧受力。其工作原理与弹簧应用相一致,即将弹簧受力形变转为传感器电信号,然后电信号转为数字信号,通过步进电机驱动平台,对输送带进行纠偏,步进电机运动中包括弹簧形变量。

为了保证数据准确性,笔者进行3次数据取样,取平均值方式读取数据。根据程序,比较指令读取数据,并与存储数据进行比较,当传感器受到力小于53 N时,认为输送带正常居中;根据压力传感器输入输出特性曲线,将53 N转化为数字9,将其作为对比值;通过比较指令接通不同辅助继电器,然后执行步进电机驱动程序,步进电机驱动到输送带边缘停留2 s后前进35 mm,再停留2 s后,复位原处。

因为此处只验证方案的可行性,所以误差测量采用目标点位和平台到达位置距离差来表示。

为测量方便,当平台达到指定位置后,将激光笔安装在平台上,测量激光笔光点中心与目标点位置距离差。其误差通过多次测量取平均值来确定。

由于设备机械结构连接与测量精度,以及监测工具方面的原因,此处只能对其进行逐点测量,每1 s测量一次距离,得到纠偏平台位置图,如图18所示。

图18 纠偏平台位置图

由图18可知:3次纠偏运行趋势是相一致的,且纠偏结果趋于0 mm,虽然存在误差,但是最终3个位置测量误差在0.2 mm～0.4 mm范围内,满足输送带纠偏定位精度要求;步进电机从开始运行到复位,用时20 s,验证了输送带纠偏装置仿真模型的可行性。

5 结束语

带式输送机在偏载工况下,由于物料偏载会对输送带造成横向冲击及跑偏,为此,笔者对物料偏载下带式输送机输送带的横向冲击特性及跑偏进行了研究,采用EDEM与ADAMS耦合插件Co-simulation实现了两者数据交换,以模拟工程实际中输送带承受物料的影响;搭建了试验平台,验证了输送带纠偏装置仿真模型的正确性。

研究结果表明:

(1)通过EDEM软件与ADAMS软件耦合,对物料与机械构件之间的相互作用进行了仿真;

(2)通过对偏载工况进行模拟可以发现,输送带在承载段受到物料横向冲击及跑偏趋势较大。因此,有必要建立输送带缓冲装置与纠偏装置。模拟结果表明,有缓冲装置的带式输送机比无缓冲装置的带式输送机输送带横向冲击与跑偏趋势均得到减缓;同时纠偏装置能够实现良好的纠偏效果,纠偏值小于带宽5%的标准,满足带式输送机行业标准。该结果表明,建立缓冲装置能够减缓输送带横向冲击及跑偏;

(3)通过搭建纠偏试验平台,并进行多次纠偏结果测量,发现误差为0.2 mm～0.4 mm范围内,符合精度要求。因此,纠偏装置是合理适用的,也验证了仿真实验的可行性。

在后续的研究中,笔者将对带式输送机纠偏结构进行进一步的优化,同时关注输送带纠偏响应及准确性研究。