大流量工况下离心泵非定常空化流动特性分析*

于 群,章 宇,王 阳,王 涛,张伟华

(1.青岛黄海学院 建筑工程学院,山东 青岛 266555;2.南方泵业股份有限公司,浙江 杭州 311106;3.中国计量大学 计量测试工程学院,浙江 杭州 310018)

0 引 言

由于具有流量较大、扬程较高、工作区域宽广的特点,离心泵被广泛应用于化工、生活供水、农业灌溉等各个领域[1-4]。

空化是离心泵应用中的常见现象,不仅会造成泵水力性能的下降和过流部件的腐蚀,还会引起机组的剧烈振动和噪音,对整个机组的安全稳定运行有很大影响[5,6]。

随着我国经济水平的快速发展,流体输送系统的重要性日益凸显,而离心泵作为流体输送的核心动力设备,其使用寿命和运行稳定性越来越受到各方的重视。对离心泵瞬态空化特性进行研究,有助于离心泵运行稳定性的提升,也可以为工程技术人员提供参考。

近年来,空化的数值模型常被用于学术研究和工程应用领域,可见,对离心泵空化的研究依旧是行业的热点[7-12]。

离心泵所应用的空化模型主要分为两大类:界面追踪模型和均相流模型。其中,界面追踪模型消耗计算资源较多,在离心泵的空化计算中应用较少;而均相流模型主要采用Rayleigh-Plesset方程的简化形式,以此来计算流场中的空化,并考虑其蒸发和冷凝过程,对体积分数在运输方程中的源项进行建模。

在离心泵空化数值预测中,最为常用的模型为Zwart、Schnerr和Singhal模型。Singhal模型考虑了非冷凝蒸汽的影响,并假定其质量分数是已知的常数。

李文广[13]采用全空化模型与RNGk-ε湍流模型,以此来预测离心泵的汽蚀性能,发现了设置非凝结蒸汽浓度为15 ppm与试验结果较为吻合。周佩剑等人[14]对单流道离心泵蜗壳内二次流漩涡进行了研究,分析了多工况下二次流强度与压力脉动的关联关系。在3个典型空化余量下,周晓红等人[15]对小流量工况下,汽车发动机冷却水泵的非定常流动进行了数值模拟计算,以及对比分析,结果表明,当空化发生时,泵内监测点的压力脉动明显降低。吴登昊等人[16]基于Zwart-Gerber-Belamri空化模型,对不同空化状态下,低比转速离心泵的流场进行了非定常计算,对不同流量下,叶轮流道内空化区域随时间的演化过程和径向力的变化规律进行了总结。杨孙圣等人[17]采用数值模拟方法,得到了临界空化余量时,叶轮内部的蒸汽体积分数分布,对空化导致泵扬程和效率下降的原因进行了分析。

由此可见,目前针对离心泵的空化研究多集中在额定流量和小流量工况[18-21],仍缺少对大流量工况下空化现象的研究,特别是对该工况下,空化与压力脉动之间关联机理的研究较少。

基于以上的原因,笔者通过实验测试泵内不同程度空化现象,测量离心泵的临界空化余量;然后,在蜗壳内建立监测点进行数值分析,得到不同监测点上的压力脉动的时域和频域特征;最后,根据数值分析情况,对不同空化状态下,叶轮内的蒸汽体积分数、中间截面速度矢量分布以及监测点压力脉动进行分析。

1 实验方法

笔者通过搭建闭式管路实验台,对离心泵外特性及不同程度空化情况进行测试。

离心泵外特性测试及空化实验台示意图如图1所示。

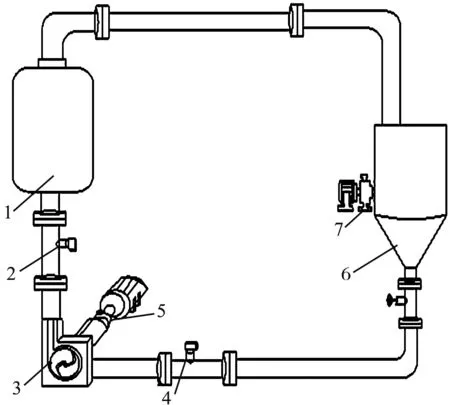
图1 实验装置示意图1—稳流罐;2—进口压力变送器;3—测试离心泵;4—出口压力变送器;5—扭矩仪;6—压力罐;7—真空泵

该实验台由闭式管路连接而成,主要的组成部分有:稳流罐、进口压力变送器、测试离心泵、出口压力变送器等。

为了达到不同的空化程度,此处在压力罐一侧安装真空泵,通过排气降低压力罐中的压力(该系统旨在测量离心泵的临界空化余量)。

由于工作条件比较复杂,离心泵在运行过程中可能会发生不同程度的空化现象。因此,此处的实验工作是在额定流量下,不断降低泵的吸入口压力,以测试泵中不同程度的空化现象;然后,根据记录的压力数据和轴功率,以此来计算泵的扬程和效率。

使用该测试方法,泵的扬程随着压力降低,刚开始基本不变,到临界点附近突然下降。这表明叶轮进口处的压力值降至低于水蒸气的压力值,即泵的临界空化现象。

2 数值模拟

此处的研究对象是一台比转速为120的单级单吸悬臂式离心泵。

该泵在设计工况下的流量Qd=300 m3/h,扬程H=45 m,叶片数为6,转速n=1 480 r/min。在数值模拟中,选择1.2Qd的大流量工况进行计算。

前期,该离心泵已经在闭式试验台上进行了实验测试。

首先,笔者对计算域进行三维建模(主要包括吸水室、叶轮和蜗壳),然后采用ICEM CFD商用网格生成器,对计算域进行网格划分。

由于泵叶片前缘处往往最早发生空化,此处需要对该区域附近的网格进行局部加密。

整个计算域由大约2.15×106网格单元组成,如图2所示。

图2 网格示意图

为了验证网格无关性,笔者采用了3.56×106网格单元进行数值模拟。经过结果对比,笔者发现,计算的扬程与2.15×106网格单元方案的结果仅相差2%。由此可见,2.15×106网格单元方案可以满足网格无关性。

在计算中,笔者采用RNGk-ε湍流模型,动量方程采用二阶迎风格式,而时间积分、湍流和蒸汽输送方程则采用了一阶格式;指定边界条件为入口压力和出口流量。

为了对空化和压力脉动的关联关系进行分析,笔者对泵蜗壳的中间截面设置压力脉动监测点。

考虑到双蜗壳的对称性,笔者在蜗壳中截面分别设置监测点P1～P5。

蜗壳中间截面监测点分布图如图3所示。

图3 蜗壳中间截面监测点分布图

考虑到残差和质量守恒情况,笔者对数值迭代的收敛性进行监控,一旦发现所有参数始终低于10-4,并且在数值迭代中基本保持恒定,则认为计算收敛。

笔者分别采用全空化模型和Zwart-Gerber-Be1amri空化模型进行计算,得到大流量工况下的临界空化曲线。

其中,全空化模型中的蒸发率经验系数为0.02,冷凝率经验系数为0.01,非凝结气体含量分别为15 ppm。

扬程随空化余量的变化如图4所示。

图4中,ZGB空化模型、全空化模型与试验值均有一定误差,但是全空化模型计算的结果与试验值更为接近。

笔者将全空化模型计算的工况A、B、C分别定义为初始空化、临界空化和发展空化。

3 数值模拟结果分析

3.1 蒸汽体积分数分析

笔者对3种不同程度空化状态下,叶轮内的蒸汽体积分数随叶轮旋转一周的变化状况进行分析。

初始空化状态下,叶轮旋转一周的叶轮流道内蒸汽体积分数的变化情况,如图5所示。

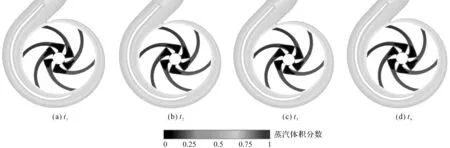
图5 初始空化状态下蒸汽体积分数分布

由图5可知:

(1)由于叶轮进口压力较低,低于此时温度下的饱和蒸气压,空泡最先发生在叶片吸力面靠近叶轮进口处;

(2)6个叶轮流道内的空泡体积分数略有不同,但是基本一致;

(3)随着叶片的旋转,在不同时刻,每个流道内的空泡体积有所变化。

临界空化状态下,叶轮内空泡体积分数的变化如图6所示。

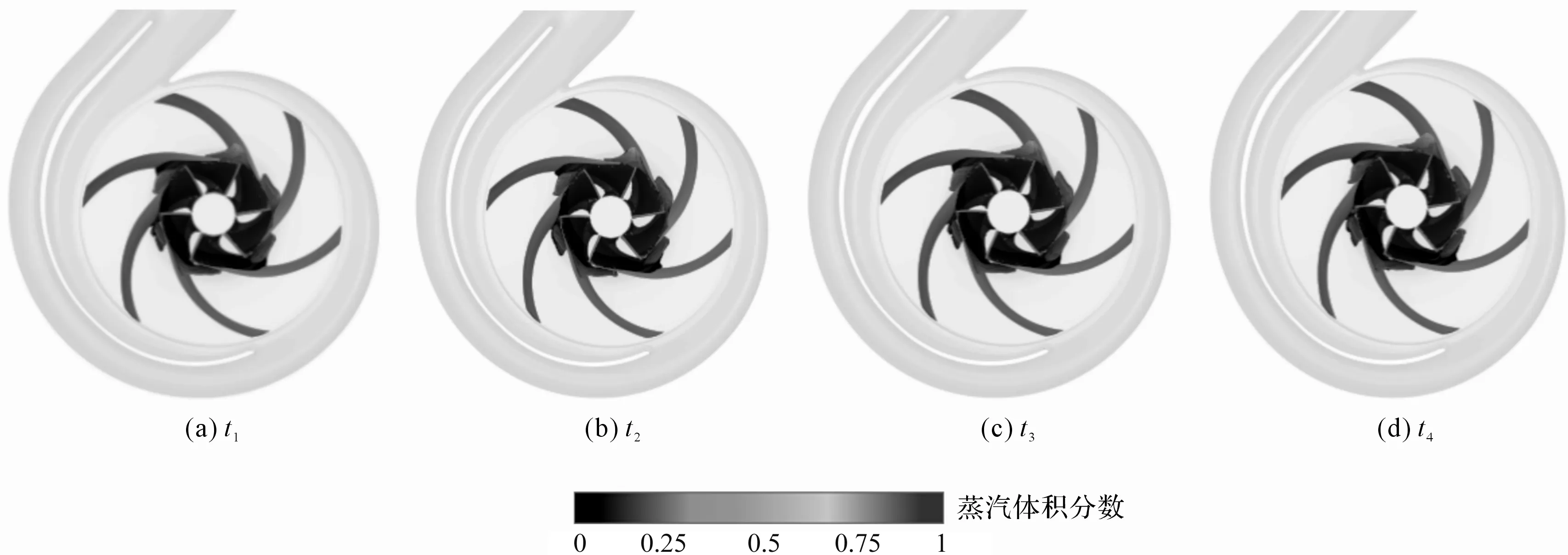
图6 临界空化状态下蒸汽体积分数分布

图6中,空化进一步发展,叶片吸力面的空泡已经延伸至相邻叶片的压力面,开始出现空泡堵塞流道的现象;随着叶轮的旋转,各叶片的空泡分布较为均匀。

发展空化状态下空泡的变化情况如图7所示。

图7 发展空化状态下蒸汽体积分数分布

由图7可以看出:

(1)空化已经进一步发展,空泡逐渐向着叶片出口方向扩展,而空泡的变大将阻碍流体的运动,能量损失增大,从而造成离心泵的扬程和效率降低;

(2)随着叶轮旋转,叶片上的空泡呈现一种由宽厚到狭长再到宽厚的规律变化。不过总体上空泡体积变化均衡。

3.2 速度矢量图变化

不同空化状态下,叶轮中间截面流体速度矢量图变化情况,如图8所示。

由图8(a)可以看到:在初始空化状态,在叶轮通道进口处产生了空穴区域,且主要附着在叶片吸力面处。

图8 叶轮中间截面的速度矢量图

由于是大流量工况,所以叶片进口处的压力面产生了流动分离,此时空穴面积和蒸汽体积分数都较小,整体上对叶轮内流场影响不大;

由图8(b)可以看到:在临界空化状态,随着空化余量的降低,空穴区域面积和蒸汽体积分数都显著增大,对流场有较大影响。叶片压力面的漩涡开始消失,在叶片吸力面上出现了较大面积的流动分离,在出口处形成了更大漩涡。

这主要是因为:伴随着空化的发展,叶片吸力面的空穴区域不断扩大,挤压了流道内流体的过流空间;流体被挤向靠近叶片压力面处,此处流动变得通畅,但在叶轮出口靠近叶片吸力面处产生了较大漩涡;

由图8(c)可以看到:当空化进一步发展,空穴区域面积和蒸汽体积分数也进一步增大,过流面积进一步变小。更多流体被挤向靠近叶片压力面处,此处流动变得更为通畅。

叶片吸力面处出现了更大面积的流动分离,在出口处形成了较大的漩涡。离心泵的水力性能已经恶化,随之而来的是其扬程和效率的急剧下降。

3.3 压力脉动变化

未空化及不同空化阶段的压力脉动时域图如图9所示。

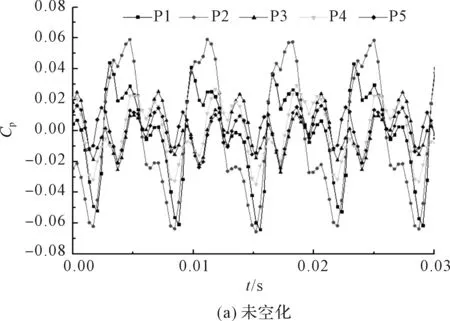
图9 未空化及不同空化阶段的压力脉动时域图

图9中,在不同空化阶段,各个测点仍具有明显的周期性。

由图9(a)可知:未发生空化时,5个监测点的压力脉动都呈现明显的周期性,因为位置不同,而有明显的相位区别。

其中,P1、P2点压力脉动的峰-峰值较大,P3、P4、P5点的压力脉动峰-峰值较小。这是因为P1、P2点在蜗壳隔舌附近,距离叶片尾缘的距离较近,叶片扫过时,该处所受的动静干涉作用最为强烈;而P3、P4、P5点距离叶片尾缘较远,所受影响较小。进一步地,可以看到P2点压力脉动波动最大,峰-峰值超过了P1点,由此可见,压力脉动最大点在隔舌附近,但并不在隔舌处;

监测点P3、P5的值相差5%左右,与P4监测点比较约有15%的差额;

在不同的空化状态下,各监测点的压力脉动依然具有周期性;

由图9(b)可知:初始空化时,各监测点压力脉动曲线更为光滑,且整体上有变小的趋势,P2点压力脉动变化幅度仍是最大;而P3、P4、P5监测点正弦化趋势增加;

由图9(c)可知:临界空化时,P1、P2监测点的压力脉动峰-峰值明显降低,且曲线的波峰区域变得更宽。而P3监测点的峰-峰值明显增大,P4、P5监测点的峰-峰值略有增大,说明此时空泡已对泵内部流场产生显著影响,引起了压力脉动的变化;

由图9(d)可知:在发展空化时,各监测点的压力脉动峰-峰值都有了显著提高,约是未发生空化时的3倍。

接下来,笔者对各个监测点的压力脉动做快速傅里叶变换。

经快速傅里叶变换,得到了未发生空化及不同空化阶段的压力脉动频谱图,如图10所示。

图10中,分别显示了各监测点在未空化时各压力脉动监测点的频域图,以及各监测点在不同空化状态下的频域对比图。

由图10(a)可知:未发生空化时,各监测点的主频均为叶频及其谐频。叶轮叶片在旋转过程中,与蜗壳之间的动静干涉作用始终占据主导;可以明显看到,P2监测点压力脉动高于其他监测点,约为其余监测点主频幅值的2～4倍;

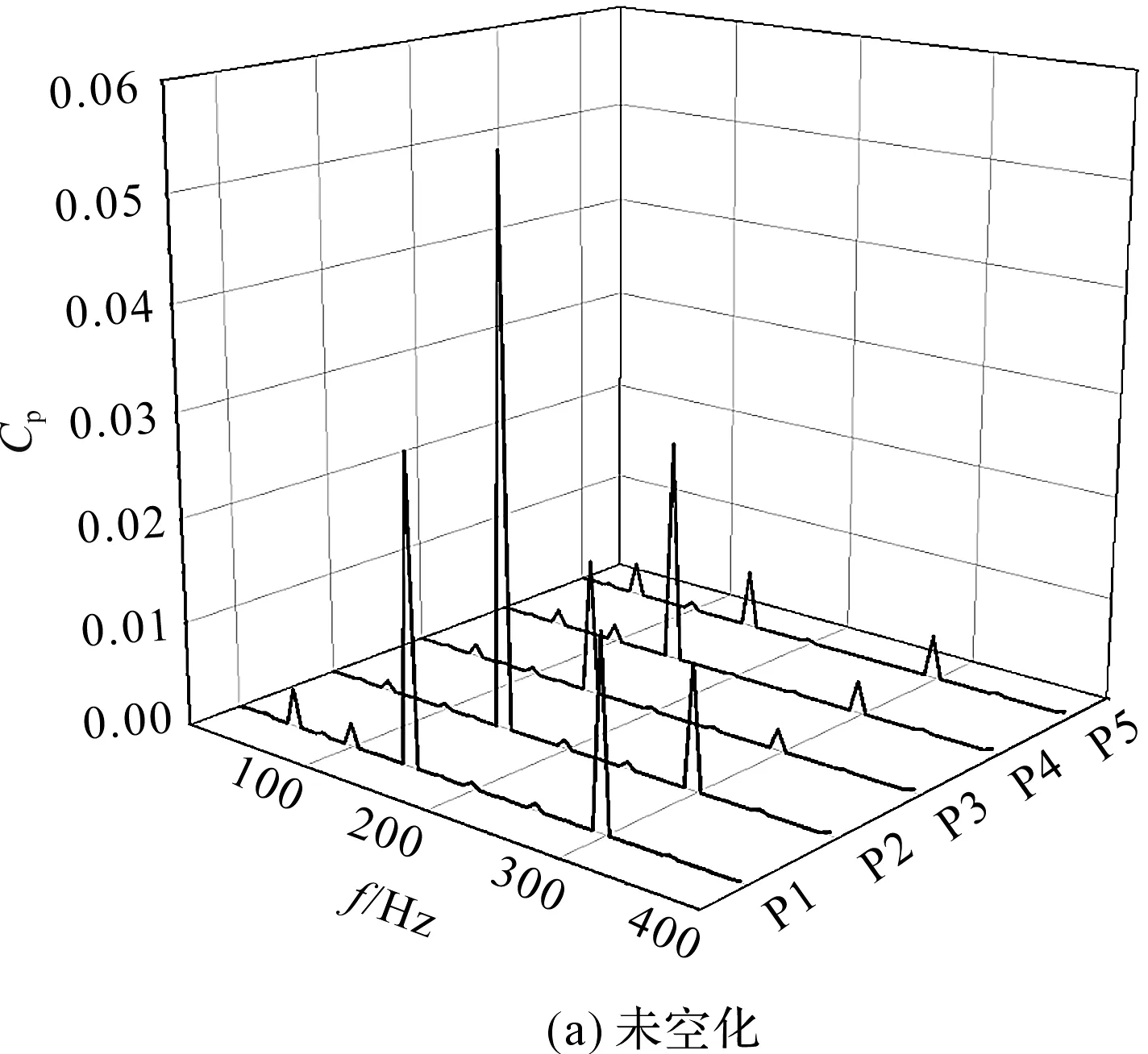
图10 未发生空化及不同空化阶段的压力脉动频谱图

由图10(b)可知:初始空化发生时,各监测点压力脉动的频域特征基本未发生改变;

由图10(c)可知:临界空化时,各监测点的压力脉动主频均为转频;

P2的主频幅值明显降低,而P1、P3监测点的主频幅值明显增大,P4、P5监测点的主频幅值略有增大,说明此时空泡已对泵内部流场产生显著影响;

由图10(d)可知:在发展空化时,各监测点的压力脉动主频均为转频;

各监测点的压力脉动主频幅值都有了显著提高,约是未发生空化的3倍。

4 结束语

由于目前针对离心泵的空化研究多集中在额定流量和小流量工况,缺少对大流量工况下空化现象,以及该工况下的空化与压力脉动关系的研究。为此,笔者通过实验测试泵内不同程度空化现象,通过在蜗壳内建立监测点进行数值分析,研究了大流量工况下,不同空化阶段,离心泵的压力脉动情况,并且对离心泵的非定常空化流动特性进行了分析。

研究结果表明:

(1)采用全空化模型和Zwart-Gerber-Be1amri空化模型进行计算对比,得到了额定工况下临界空化曲线;两者与试验值均有一定误差,但是全空化模型计算结果与试验值更为接近;

(2)随着空化加剧,叶片吸力面的空穴区域不断扩大,挤压了流道内流体的过流空间。流体被挤向靠近叶片压力面处,此处流动变得通畅,而叶片吸力面上出现了大面积的流动分离,并在出口处形成较大漩涡;

(3)在不同空化状态下,蜗壳上压力脉动各监测点的主频均为转频或转频的谐频;在发展空化状态下,各监测点的压力脉动主频幅值都有了显著提高,约是未发生空化的3倍。

在下一研究阶段,笔者拟对空化模型进行修正,以提高对离心泵空化的预测精度;并对小流量条件下,空化与涡流之间的交互影响进行研究,以此来揭示不同工况下的空化影响机理。