基于威布尔分布的谷物干燥机可靠性分析*
文昌俊,陈 哲,徐云飞,邵明颖,左学谦
(1.湖北工业大学 机械工程学院,湖北 武汉 430068;2.湖北省现代制造质量工程重点实验室,湖北 武汉 430068)
0 引 言
在众多的农业机械设备中,谷物干燥机的应用较为广泛。作为一种重要的粮食贮存设备,谷物干燥机一旦在作业季出现故障频发的情况,就会导致谷类储存过程中产生大量直接或间接的粮食损失。因此,保证谷物干燥机的平稳、无故障运行,提高其生产效率,并减少其生产损失,其意义重大。
迄今为止,国内大部分行业依旧延用传统的后期维护或定期维护的方案,频繁出现“维护不足”或“维护过度”的现象[1,2],因此造成了巨大的资源浪费。在这种情况下,预防性维修的策略逐渐得到了应用,而可靠性分析在预防性维修中又起着十分重要的作用。
目前,在农业机械产品上的可靠性分析与评价理论还不够完善。尽管有关于针对电子设备类产品的安全性研究已经比较完善,但由于农业机械产品和电子设备之间存在着很大的差异,无法将针对电子设备类产品的安全性研究成果充分应用到农业机械产品的可靠性分析与评价上来。
穆艳等人[3]在对真空断路器进行可靠性分析过程中,利用实验数据建立了威布尔分布模型,并用Mann检验法验证了模型,得到了模型的评价指标和断路器的平均寿命。王亚菲等人[4]在针对汽车寿命估计方法的研究中,在进行威布尔参数估计时,对分别采用极大似然估计法和神经网络估计法获得的结果进行了对比,证明了该方法的适用性。在对城轨计轴设备进行可靠性评估研究过程中,牛儒等人[5]以现场的真实数据为出发点,确定了城轨计轴设备失效率的概率分布。孙扩等人[6]基于飞机历年的故障数据,建立了其三参数威布尔模型,对该型飞机进行了故障预测,并对模型和预测方法的可行性进行了验证。
然而在上述研究中,研究人员在选择模型时没有进行模型先验,或者在进行参数估计时没有进行参数估计方法的对比,故都影响了其分布模型的选择,或导致其参数估计精确度不高,从而影响分析结果的有效性和准确性。
因此,为了提高谷物干燥机的使用寿命,减少故障维修次数,笔者运用可靠性分析理论对其使用寿命进行分析研究。
笔者依据历史维修数据获得试验数据,并进行数据预处理,即首先利用图形法先验模型,然后利用点估计的优良性判别准则选择合适的参数估计方法,随后检验模型的合理性,建立谷物干燥机的可靠性模型,并计算得到谷物干燥机的可靠性指标和平均故障间隔时间。
1 威布尔分布与检验方法
笔者针对谷物干燥机的故障数据展开研究,首先整理谷物干燥机的相关维修记录,利用概率统计理论分析结果,得出谷物干燥机的故障间隔时间,得到威布尔概率图,拟确定使用威布尔分布来对这列数据进行建模,随后利用最小二乘法和极大似然估计分别对威布尔参数进行计算,比较得出最优的参数值,最后利用K-S检验法确定模型的合理性。
1.1 威布尔分布
机械产品常用的寿命分布主要有威布尔分布、指数分布、正态分布等。其中,威布尔分布为近年来在设备寿命可靠性分析中使用最普遍的模型之一,其形状参数取值范围能够整体描述出“浴盆”曲线的各个阶段。
威布尔分布的机理是根据故障的寿命数据研究机械产品的寿命与其可靠度之间的关系。威布尔分布有二参数和三参数两种形式。当其位置参数γ≠0时,为三参数威布尔分布;反之,当γ=0时,则该分布为二参数威布尔分布。
谷物干燥机的故障间隔时间符合威布尔分布模型,模型随机变量为干燥机寿命t,由于干燥机在零小时内开始运行,故障是随机的,可能从任务开始就发生,因此,干燥机的威布尔模型的位置参数为零,即γ=0。
综上所述,可得干燥机的寿命模型为二参数威布尔分布,则相应的故障概率密度函数、故障概率分布函数和可靠度函数分别为:
(1)
(2)
(3)
式中:m—形状参数;η—尺度参数。
当m不变时,η值不同时概率密度曲线的高度和宽度均不相同;m为形状参数,根据m值的不断变化,其故障概率密度曲线、故障概率分布曲线和可靠度曲线都会随之变化。
其中,当m<1时,f(t)的曲线随时间单调下降,对应“浴盆”曲线的早期失效阶段;当m=1,f(t)曲线对应“浴盆”曲线的随机失效阶段,此时曲线类似于指数分布;当m>1时,f(t)曲线对应“浴盆”曲线的耗损失效阶段。
1.2 K-S检验法
在数理统计中,选择正确的统计方法至关重要[7-9],它决定最后结果的正确与否。常用的检验样本分布类型[10]的方法为K-S检验法和χ2检验。其中,K-S检验法是一种可以不用根据数据的分布情况而进行检验的非参数检验方法[11]。相比χ2检验的使用条件,在不知道谷物干燥机现场试验数据的分布情况下,显然K-S检验法更加适用且有效。
K-S检验法可用来检验一组样本数据的分布与指定的某一理论分布之间的符合程度。
将假设的理论概率分布F(t)与样本观测值的累积分布函数F0(t)进行比较,找出它们之间最大的差异点,并参照抽样分布,可以确定该差异是否处于偶然。
笔者设总体分布为F(t),F0(t)为已知的连续分布函数,假设检验问题H0为:F(t)=F0(t),则K-S检验步骤如下:
(1)求解分段累积频率:
(4)
式中:样本量为n的样本x1,x2,x3,…,xn—从小到大排列之后的样本数据;Fn(t)—经验分布函数。
(2)计算样本累积分布函数与理论概率分布的绝对差,令最大的绝对差为Dn,其表达式为:
(5)
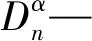
若满足式(5),则认为接受假设H0;反之,则不接受。
2 参数估计及拟合优度检验
2.1 数据处理与分析
此处,笔者以某企业作业季度的18台某型号谷物干燥机历史维修数据为例进行实验。
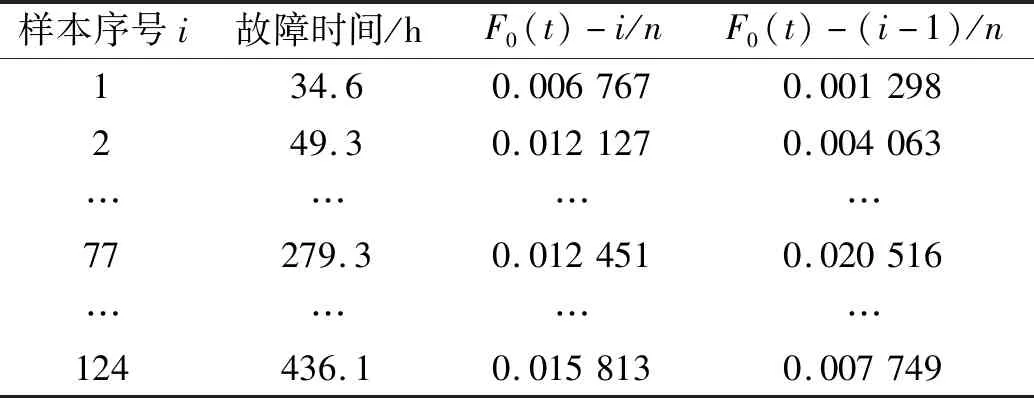
笔者共收集到194组故障数据,经过数据清洗整理剩下有效故障数据124组,将124组故障间隔时间按从小到大的顺序排列后,如表1所示。
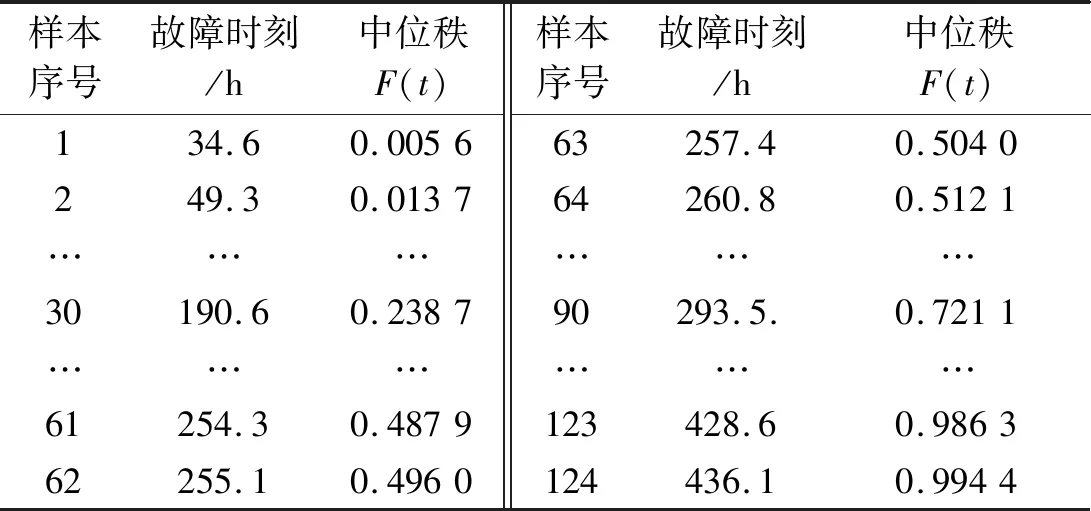
表1 谷物干燥机故障数据表
由于威布尔分布模型[12-13]具有较强的适应性,而谷物干燥机的失效主要是由机械故障引起的,故笔者首先假设其符合威布尔分布,再通过MATLAB绘制出谷物干燥机的威布尔拟合效果图,即威布尔概率图(WPP)图,如图1所示。

图1 谷物干燥机威布尔拟合效果图
从图1中可以看出:大部分数据近似呈现一条直线分布,所以可以初步认定该组数据服从威布尔分布。
2.2 参数估计
在初步确认数据服从于二参数威布尔分布后,笔者随后进行模型的参数估计。
为了保证谷物干燥机可靠性模型的准确性与精确度,笔者分别采用最小二乘法和极大似然估计对模型的参数进行计算,并通过对比得出其最优的参数值。
2.2.1 最小二乘估计(LSM)
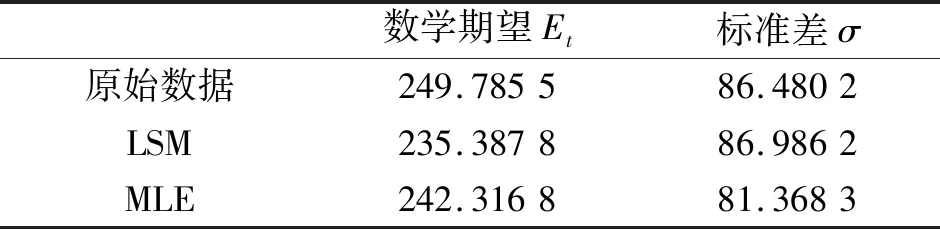
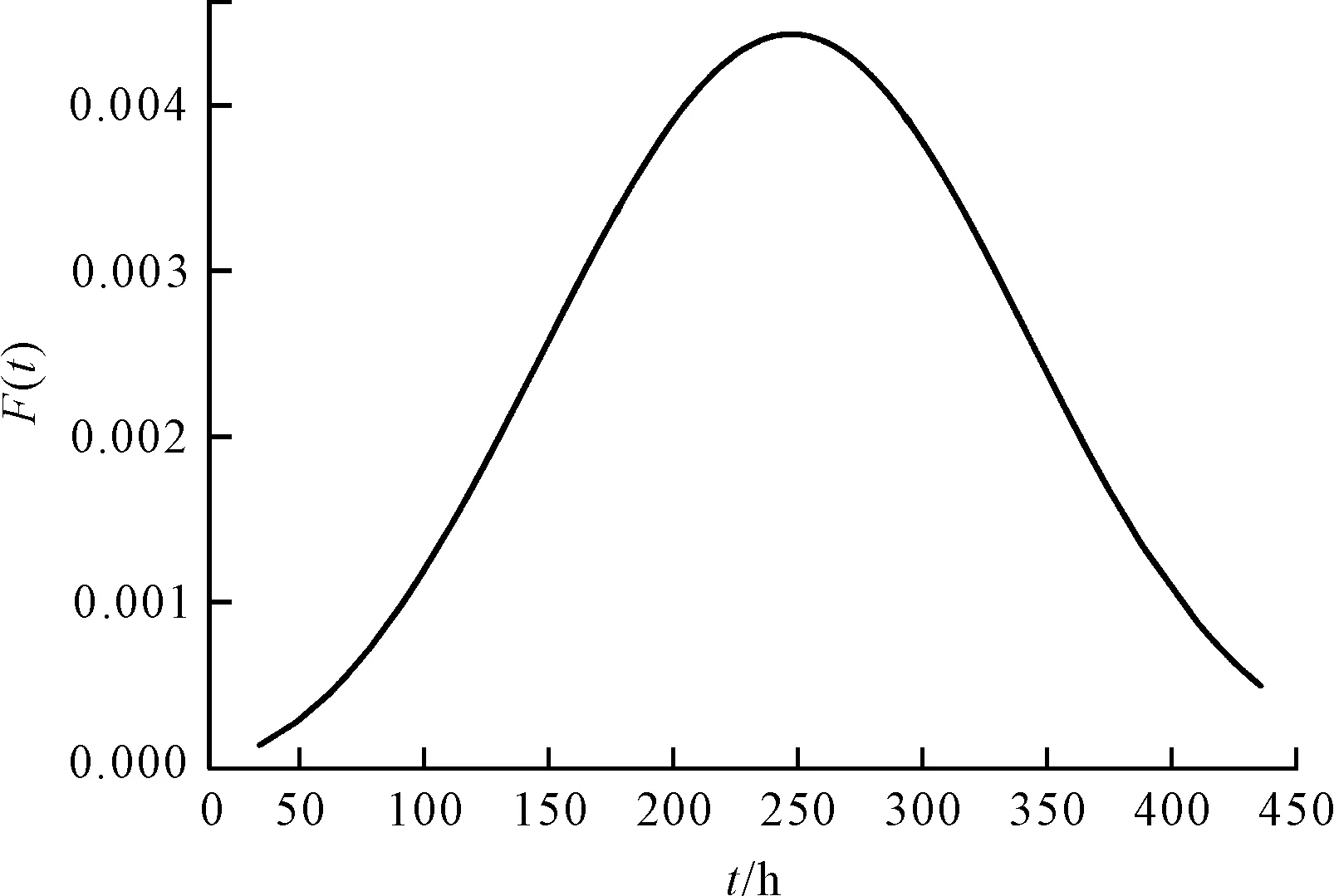
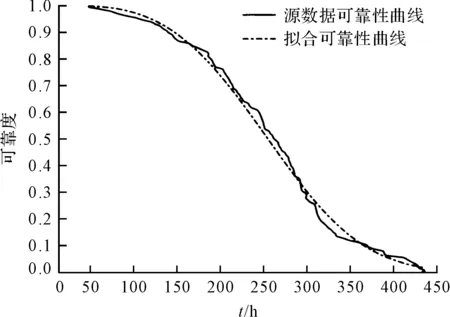
假设某型谷物干燥机在试验周期内共发生n次故障,其故障发生时间从小到大依次排序为t1 将数据{(ti,F(ti))}(i=1,2,…,n)代入式(2),然后对其连续取两次对数,经线性化处理后可得: (6) (7) 根据回归分析法则,可以推导得出参数a、b、m和η的估计值表达式为: (8) (9) (10) 得到如上关系式后,采用近似中位秩公式的计算值作为F(t)的估计值。 2.2.2 极大似然估计(MLE) 直接将故障间隔时间代入式(1),并对其求对数,可得到似然函数如下: (11) 笔者对式(11)中的m和η分别求偏导数,可得似然方程组,对方程组进行整理后可得: (12) 根据点估计[14,15]的优良性判别准则,笔者采用无偏性和有效性作为参数估计值的选定标准,经过计算得出了其结果,如表2所示。 表2 有效性与偏差性对比表 由表2的数据可知:最小二乘法的数学期望误差百分比为5.76%,标准差为86.986 2。极大似然估计的数学期望误差百分比为2.99%,标准差为81.368 3。 与最小二乘法相比,最大似然估计得到的威布尔分布模型的数学期望值接近于干燥机故障样本的平均值;最大似然估计得到的模型标准差小于最小二乘法得到的模型标准差。 结果模型的标准偏差表明:通过最大似然估计获得的模型内个体之间的离散程度较低。 (13) 联立式(4,5)可得: (14) 经计算得出了相关的结果,如表3所示。 表3 谷物干燥机寿命分布检验 在确定了威布尔分布模型[16-19]的形状参数m和尺度参数η后,笔者把计算结果代入式(1~3)中,得到谷物干燥机相关的可靠性基本函数。 谷物干燥机的概率密度曲线如图2所示。 图2 谷物干燥机的概率密度曲线 由图2可看出:谷物干燥机故障间隔时间的概率密度函数的极大值点在249 h左右,说明了此类干燥机的无故障工作时间的大众数是249 h,这也就意味着在正常工作249 h以后,要进行一定程度的大修,故原来规定的预防性保养时间在249 h。 同时,可得出对应的谷物干燥机故障概率分布曲线,如图3所示。 图3 谷物干燥机的故障概率分布曲线 由图3可发现:随着谷物干燥机工作持续时间的增长,不可靠率也将相应提高;到了150 h时,函数斜率明显上升,因此,故障率也开始增加。 谷物干燥机故障间隔时间的故障概率密度函数和故障概率分布函数分别为: (15) (16) 谷物干燥机的可靠度函数为: (17) 谷物干燥机的可靠性趋势图如图4所示。 图4 谷物干燥机的可靠性趋势图 由图4可以看出:通过计算得出的威布尔分布与源数据样本的拟合效果较好,能比较准确地预测出谷物干燥机的失效趋势。 为了保证谷物干燥机的可靠性,可取可靠度R(T)为0.9来计算预防性维修周期。 在R(t)≥R(T)的条件下,谷物干燥机的工作周期为: T=η(ln(1/R(T)))1/m (18) 将威布尔分布的形状参数和尺度参数代入式(18)中,可得谷物干燥机的预防性维修周期随着可靠度的减小而增大。 笔者取不同的可靠度进行计算。不同可靠度下的干燥机预防性维修周期,如表4所示。 表4 不同可靠度下的干燥机预防性维修周期 由表4可知,在R(T)为0.9时,预防性维修周期为137.6 h。 平均故障间隔时间公式如下: (19) 根据平均故障间隔时间公式,经计算可得干燥机的平均寿命MTBF=249.8 h。 综上所述,249 h小于谷物干燥机的平均寿命。该结果表明,原规定的定期检修时间是合理的。 为了提高谷物干燥机的使用寿命,减少故障维修次数,笔者运用可靠性分析理论对其使用寿命进行分析研究。 即根据谷物干燥机的相关维修数据,笔者首先采用图形法对数据进行先验处理,建立了威布尔分布的拟合模型,并利用点估计的优良性判别准则,选取极大似然估计法计算确定了威布尔模型的参数;然后利用K-S检验方法验证了拟合模型的合理性,并计算得到了相应的分布函数和可靠性指标,进一步优化了预防性维修周期;最后对谷物干燥机的可靠性进行了评估。 研究结果如下: (1)谷物干燥机是十分重要的农业设备,将可靠性分析理论运用在其运行规律上可以得到相应的可靠性指标,从而进一步提高设备的可靠性; (2)与最小二乘法相比,极大似然估计得到的参数值可以更准确的建立威布尔分布模型,并计算得到了平均故障间隔时间(249.8 h)和预防性维修周期(137.6 h)。 在后期的工作中,笔者将针对谷物干燥机的维修性进行研究,将干燥机的可靠性和维修性相结合,来共同对谷物干燥机的质量情况进行评估。
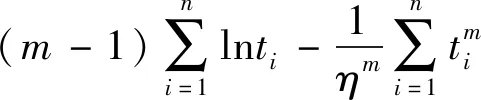


2.3 拟合优度检验


3 谷物干燥机可靠性分析

3.1 故障概率密度函数和分布函数
3.2 可靠度函数

4 结束语

