基于S变换与奇异值中值分解的滚动轴承故障诊断*

字 玉,周 俊

(昆明理工大学 机电工程学院,云南 昆明 650500)

0 引 言

滚动轴承属于常用的机械零部件之一,它关系到转子能否正常工作,而它也是出现故障概率较高的机械设备部件之一[1,2]。

当服役中的轴承发生故障时,转子轴便无法正常工作,甚至会产生抖动,在一定程度上影响机械设备的正常运行。如果没有及时检测到服役滚动轴承故障,可能会导致设备瘫痪[3]或者重大事故的发生,甚至威胁到人身安全。

因此,对轴承的运行状态进行实时监控十分有必要,它不仅能节省开支,保证设备的正常工作,还可以避免重大安全事故的发生[4,5]。

S变换是Stockwell在研究地球物理学时提出的一种将信号从一维时域信号变换到二维时域信号的信号处理方法。作为小波变换和短时傅里叶变换的继承和发展,S变换采用高斯窗函数且窗宽与频率的倒数成正比,免去了窗函数的选择和改善了窗宽固定的缺陷,并且时频表示中各频率分量的相位谱与原始信号保持直接的联系,使其在故障分析中可以采用更多的特征量;同时,S变换提取的特征量对噪声不敏感。因此,近年来众多学者纷纷采用S变换作为分析工具。S变换适用于处理和分析各类故障信号,尤其是在提取信号冲击特征方面,具有较为显著的优势。

目前,放眼国内外,变换已经在各个领域得到了广泛的应用,尤其是在地震信号处理方面。

刘乃豪[6,7]提出了一种采用S变换进行地震震相识别的方法,为地震预警和地震应急提供了新的手段。

在电能质量扰动方面,徐方维[8]提出了一种基于S变换时频模矩阵的电能质量短时扰动分类新方法,结合能量归一化概念,以及分频逐级计算相似度的思想,实现了各类扰动信号之间的差异。

在故障诊断方面,杨先勇[9]提出了一种基于极大形态小波分析和S变换的滚动轴承故障特征提取方法;由于在尺度信号上保留了信号的局部极值特征,该特征提取方法适用于对信号故障特征进行在线分析。潘高元[10]提出了一种同步挤压S变换方法,该方法兼顾了S变换和同步挤压变换的优势,能够方便、有效地提取出轴承故障的周期性冲击特征。

在故障诊断领域,因为S变换具有易于处理信号冲击特征的特点,所以其具有巨大的优势。

要提取滚动轴承故障冲击特征信号,需要从两方面入手:(1)分析信号的高阶统计量,这些值和信号的冲击特征关系密切,利用峰态、峭度、偏斜度等可以识别信号的冲击特征[11-14];(2)直接对采集到的振动信号进行降噪,用这种简单、直观的方式便可以提取出故障冲击特征信号。

奇异值分解可以有效滤除信号中的杂波,在一定程度上保留所需要的冲击特征信号[15]32-33,再结合韩孝明[16]对奇异值分解方法中的奇异值差分谱法、特征均值法、奇异值中值法进行对比,便可得到奇异值中值法对实测信号降噪效果最优的结论。

因此,笔者提出一种基于S变换与奇异值中值分解(SVMD)的方法,对轴承的振动信号进行降噪,进行冲击特征信号的提取[17]。

首先,笔者利用S变换对振动信号进行时频变换,得到时频系数矩阵;然后,对时频系数矩阵采用SVMD方法筛选奇异值来降噪;用S逆变换对降噪后得到的数据矩阵进行变换,并用还原后的信号模拟原始信号的时域冲击特征;最后,用仿真信号和实际轴承故障实验对算法的有效性和准确性进行验证。

1 理论基础

1.1 S变换

基于时频分析的研究,STOCKWELL R G等人[18,19]提出了S变换。S变换是一种时频分析的工具。和其他时频分析工具一样,透过S变换,可以同时从时域以及频域观察一个信号的能量分布。

S变换的特别之处在它既保持与傅里叶变换的直接关系,又可在不同频率有不同的分辨率。此外,S变换与小波变换(wavelet transform,WT)有密切的关系。S变换不仅可以看作可变窗口的短时傅里叶变换,还可以看作在相位修正基础上进行的小波变换。

目前,S变换方法现在已经成功运用在各种领域,尤其在信号分析领域更是得到了广泛运用。

信号x(t)的S变换可表示为：

(1)

式中：f—频率；τ—时移参数；ω—可变高斯窗。

其中，可变高斯窗ω的表达式为：

(2)

S变换在信号的频域角度可表示为：

(3)

式中：v—频移参数。

S变换以小波变换为基础,并乘以一个相位因子,以此将二者的优势结合,融合了二者的特点;再利用快速傅里叶变换进行运算,提高了工作效率,在分析复杂信号方面具有较为显著的优势。

目前,S变换已被广泛应用于时频分析领域。它摆脱了短时傅里叶变换分辨率的束缚,排除了Wigner-Ville的干扰,降低了小波变换[15]30对于基小波的依赖程度,因此,成为时频处理领域不可或缺的一种方法。

基于以上优点,在此处笔者采用S变换对振动信号进行时频变换处理。

1.2 奇异值中值分解

奇异值分解(singular value decomposition,SVD)是线性代数中一种重要的矩阵分解工具,它揭示了矩阵最本质的变换,在信号处理、统计学等领域有着广泛而重要应用。使用SVD对矩阵进行分解,能得到代表矩阵最本质变化的矩阵元素。

令A为m×n的矩阵，秩为r(r≤n)，则存在m×n的正交矩阵U和n×n的正交矩阵V，使得：

A=UDVT

(4)

式中：D—m×n的非负对角阵。

m×n的非负对角阵D的表达式为：

(5)

σ1,σ2,…,σr连同σr+1=…=σn=0是A的奇异值。因为A矩阵是由信号和噪声构成，所以由奇异值σ1,σ2,…,σr可以看出信号和噪声的能量聚合情况。

若将σ1,σ2,…,σr按照从高到低的顺序排列起来，当r是偶数时，中值为第r/2位数和第(r+2)/2位数的平均值；当r是奇数时，中值为第(r+1)/2位数的值。

将小于奇异值中值的奇异值置零,判断奇异值的个数,重新构建矩阵,从而可以对信号进行降噪处理。

2 基于ST-SVMD的冲击特征提取

由于混合信号x(t)是典型的非高斯、非平稳信号,而要提取出混合信号x(t)中的有效冲击特征,需要首先对其进行变换。

此处,笔者采用S变换和奇异值中值分解(ST-SVMD)算法对混合信号x(t)进行变换,其具体的流程图如图1所示。

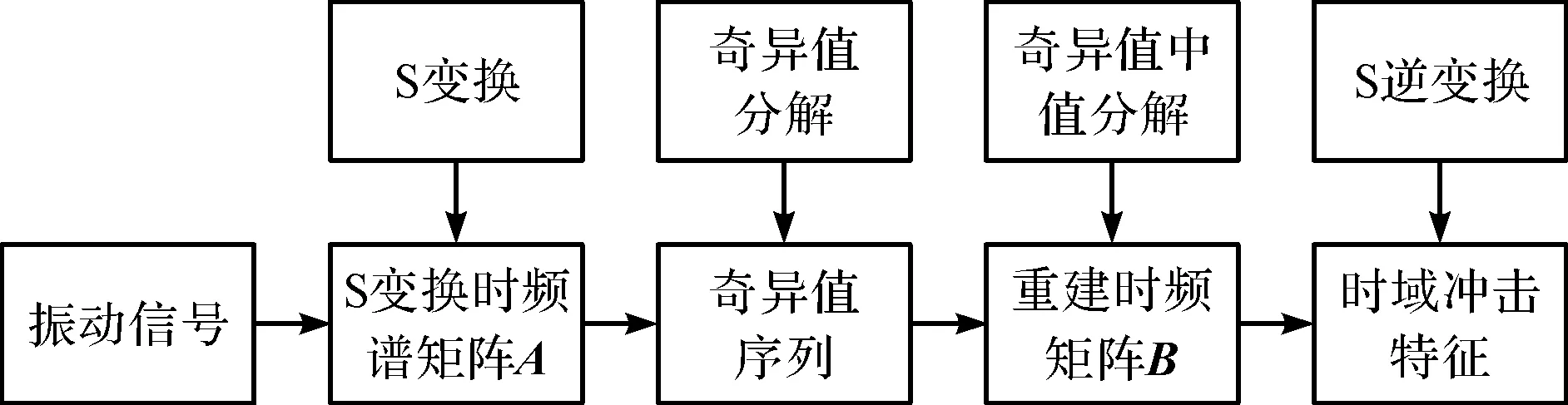
图1 基于S变换和奇异值中值分解的流程图

基于S变换时频谱和奇异值中值分解(SVMD)降噪的冲击特征提取步骤如下:

(1)对x(t)进行S变换,获得S变换时频谱系数矩阵A。其中,A是N×N的矩阵,N是混合信号x(t)采样长度;

(2)对矩阵A进行奇异值中值分解(SVMD),算出矩阵A的奇异值,再将这些奇异值从大到小进行顺序排列,即σ1≥σ2≥…≥σN,并且令非零奇异值序列为∑=(σ1,σ2,…,σr),再计算出这个序列的奇异值中值σmwdian;

(3)将阈值设置为奇异值的中值σmwdian,并将奇异值序列中小于或等于σmwdian的奇异值置零,然后得到新的S变换时域谱系数矩阵B。经过以上步骤,即可达到降噪的目的;

(4)对矩阵B进行S逆变换,提取x(t)的冲击特征。

3 冲击信号特征提取仿真

为了验证上述算法能否有效提取出信号的冲击特征,接下来,笔者人为地生成一个噪声混合信号,采用基于S变换和SVMD的算法进行冲击信号的特征提取。

仿真一个指数衰减信号模型，它的冲击成分p(t)可表示为：

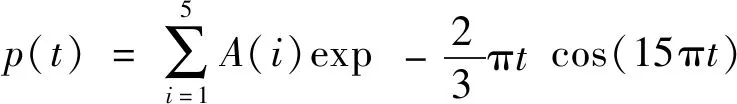
(6)

其中，振动信号幅值序列A(i)(i=1,2,…,5)为均值μ=2，标准差σ=0.3的高斯随机序列。

仿真信号的处理图如图2所示。

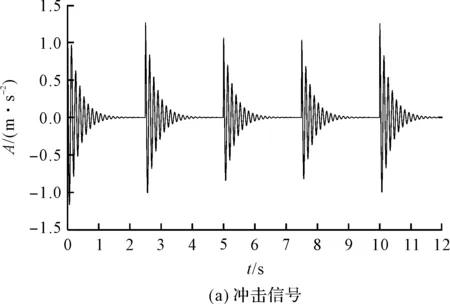
图2 仿真信号处理图

图2(a)中,p(t)为仿真信号x(t)中的冲击成分;

图2(b)中,叠加上高斯白噪声后,变成信噪比为-4的仿真信号x(t)。从图中可以明显看出,x(t)中的冲击成分p(t)已经淹没在周围信号中;

图2(c)中,对仿真信号x(t)进行S变换,可以得到其时频谱。由于存在强烈的背景噪声,无法清晰地从图2(c)中观察到仿真信号x(t)中的周期性冲击特征;

图2(d)中,对S变换谱系数矩阵进行奇异值分解,其目的是获得奇异值谱,得到奇异值个数为1 001,此处选取σmwdian=501;

图2(e)中,对S变换谱进行SVMD降噪处理;

图2(f)中,对降噪后的时频谱进行S逆变换,提取出仿真信号x(t)中的时域冲击特征p(t)。

综上所述,基于ST-SVMD的算法可以在一定程度上提取出仿真信号x(t)的冲击特征。虽然如图2(a,f)所示,提取到的冲击特征有一些变形和失真,但仍然可以准确得到冲击特征所出现的频率。

4 故障实验

为了验证基于ST-SVMD算法的有效性,笔者再次以轴承外圈、滚动体故障为例,进行轴承的外圈和滚动体故障数据分析处理的模拟实验。

此处所用实验台为QPZZ-Ⅱ旋转机械振动分析和故障模拟实验系统。

笔者选用轴承N205外圈、滚动体故障进行模拟实验。

轴承N205故障滚动轴承相关参数如表1所示。

表1 故障滚动轴承相关参数

参考轴承手册,可以得到轴承各个部分的故障特征频率参数:实验转速为800 r/min,可以得到转频13.3 Hz,内圈故障特征频率95.15 Hz,外圈故障特征频率64.45 Hz,滚动体故障特征频率5.38 Hz。

试验台及传感器布置图如图3所示。

图3 试验台及传感器布置图

由图3可以看出加速度传感器在试验台上的位置。

图3中的加速度传感器是磁铁的,可以吸在轴承端盖表面,采用NI Signal Express采集模块和NI-9234采集卡对故障信号进行采集;其采样频率fs=8 192 Hz,采样点数N=8 192。

实验故障类型分别为轴承外圈故障和滚动体故障。

5.1 外圈故障

实验过程中获得的滚动轴承外圈故障信号处理图,如图4所示。

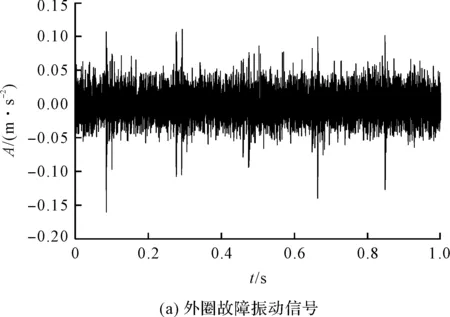
图4 外圈故障信号处理图

轴承外圈故障的原始振动信号如图4(a)所示;对外圈故障振动信号进行S变换,得到的时频谱如图4(b)所示,再经过奇异值中值降噪,最终得到的时频谱如图4(c)所示,信号时域波形如图4(d)所示。

通过计算可得出其最小冲击特征周期约为Δt1=0.015 09 s,得到其频率为66.269 Hz。

由于滚动轴承外圈的故障特征频率为64.45 Hz,可见其与所算频率基本一致。

5.2 滚动体故障

实验过程中获得的滚动轴承滚动体振动信号[20，21],即故障信号处理图,如图5所示。

轴滚动体故障的原始振动信号如图5(a)所示;

对保持架故障振动信号进行S变换后时频谱如图5(b)所示;

再经过奇异值中值降噪以后的时频谱如图5(c)所示,信号时域波形如图5(d)所示。

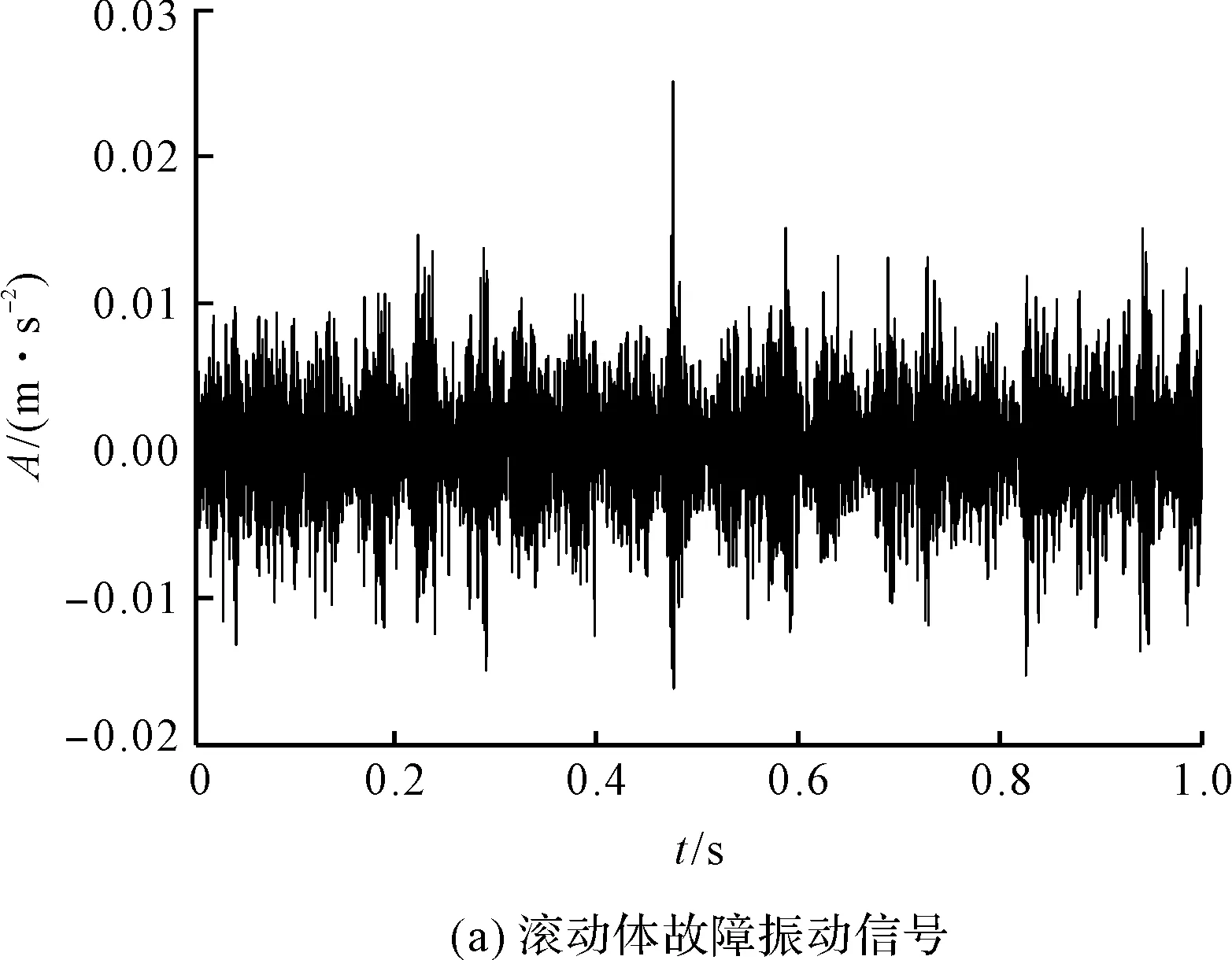
图5 滚动体故障信号处理图

通过计算可得出最小的冲击特征周期约为Δt2=0.187 4 s,得到其频率为5.336 Hz,保持架的故障特征频率5.3 Hz和算出频率基本一致。

5 结束语

为了有效地提取出滚动轴承故障信号的冲击特征,笔者提出了一种基于ST-SVMD算法的滚动轴承故障诊断方法。

笔者首先采用S变换(ST)对振动信号进行时频变换,算出时频系数矩阵;然后,采用奇异值中值分解(SVMD)对时频系数矩阵进行计算,筛选出合适的奇异值来降噪;最后,对上述结果进行S逆变换,获得信号的时域冲击特征。

其中,S变换时频谱能为奇异值中值分解(SVMD)提供合适的数据矩阵,将小于奇异值中值的各个奇异值置零,保留大于奇异值中值的各个奇异值,最终达到降噪的目的。

研究结果表明:

(1)对于仿真信号,ST-SVMD算法可以在一定程度上提取出其冲击特征,虽然有一些变形和失真,但是仍可以准确地得到冲击特征所出现的频率;

(2)对于实测信号的外圈故障信号,采用ST-SVMD算法可得到其频率为66.269 Hz,滚动轴承外圈故障特征频率64.45 Hz,与所算频率基本一致;

(3)对于实测信号的内圈故障信号,采用ST-SVMD算法可得到其频率为5.336 Hz,滚动体的故障特征频率5.3 Hz,与所算频率基本一致。

在后续的工作中,笔者将对S变换的参数进行优化,降低对参数调整的依赖,提高其自适性;同时,尝试将ST-SVMD应用于更多的设备故障诊断中,扩大其应用范围和领域。