一类改进的谱共轭梯度法

陈秀芳，李 锋

(1.滇西科技师范学院 数理学院 ，云南 临沧 67700;2.云南师范大学 数学学院 ，云南 昆明 650500)

考虑如下无约束优化问题

(1)

其中：函数f:Rn→R上是连续可微函数.共轭梯度法(CG法)是Stiefel与Hestenes于1952年提出了一种求解线性方程组的算法,随后，Reeves与Fletcher在1964年将该方法推广到求解非线性优化问题，提出了如下非线性共轭梯度法[1]：

xk+1=xk+αkdk,k=0,1,2，

(2)

其中xk为当前迭代点，搜索步长αk由合适的线搜索(精确和非精确)确定，搜索方向dk由以下公式给出：

(3)

共轭梯度法具有占用存储空间小、收敛速度快的特点，广泛应用于控制科学、工程管理和流程研究等领域，在近年来兴起的大数据科学显示出特别的吸引力，因而一直受到学者们的广泛关注，相关研究持续不断.

共轭梯度法的改进线索大致分为2条，一条是修改共轭系数βk(称这类算法为经典CG算法)，另一条是融合谱最速下降法的思想，引入谱系数(称这类算法为谱共轭梯度法).

经典CG算法分为2类：第1类包括Fletcher-Reeves(βkFR)[2]、Dai Yuan(βkDY)[3]公式如下：

(4)

其中‖·‖为Euclidean范数，yk=gk+1-gk，这些方法有很好的收敛性，然而数值性能却不是很好.另一类包括Polak-Ribiére-Polyak(βkPRP)[4]、Hestenses-Stiefel(βkHS)[5]、Liu Storrey(βkLS)[6]，它们的βk公式分别如下:

(5)

这类方法收敛性分析不是很理想，然而数值实验结果较为良好，且PRP方法和HS方法被公认为最有效的CG法.鉴于上述2类方法优缺点互补的特点，学者们提出了把2种系数组合起来的混合共轭梯度法.2006年Wei等[7]提出一个新的共轭参数βk，βk与经典的PRP公式有类似的形式，并且首次将线性组合的思想引入经典共轭梯度法中，公式如下：

(6)

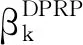
(7)

(8)

韦等在复杂线搜索下建立了新的PRP型共轭梯度法，并讨论相关的问题.

鉴于经典CG算法是基于最速下降的改进算法，2001年Birgin和Martinez[12]基于谱梯度法提出了谱共轭梯度法(SCG法)，即在经典共轭梯度法的搜索方向dk的迭代格式(3)中引入谱系数δk：

(9)

对应的参数分别为：

(10)

景书杰等在Armijo线搜索下证明算法全局收敛，综合前面2条线索，得到一个好的结果.沿着这个线索，大有工作可做.有关谱共轭梯度法的其他变种还很多，可以参看文献[17-21].

文中深受上述讨论的启发，尤其是文献[11]和[16]中2个参数的构造.从这些算法的发展可以发现，确定不同的系数，算法的表现不一样.文中尝试用前面的思路确定2个系数的新公式，并讨论他们的收敛性及相关问题，其它工作安排如下：第1节算法及其下降性，第2节算法的全局收敛性，第3节数值实验，第4节全文总结.

1 算法及其下降性

(11)

其中，

(12)

该算法采用修正的强Wolfe线搜索求步长

其中,0<ρ<σ<1.

算法1：

谱共轭梯度法算法流程如下：

Step 0 初始值x0∈Rn,ε>0,令μ>0,λ>0,0<ρ<σ<1,k:=1,d1=-g1,Step 1 计算gk,若‖gk‖≤ε,则停止,否则转Step 2,Step 2 用强Wolfe线搜索公式计算αk,Step 3 用式(11),(12)分别计算dk,βFk,δk,Step 4 令xk+1=xk+αkdk求gk+1,并用式(11)求βFk+1,使得dk+1=-δk+1gk+1+βFk+1dk,使得k:=k+1,转Step1.

算法的收敛性证明需要以下假设条件成立

假设A[21]：

(i)定义目标函数f(x)在水平集L0={x∈Rn|f(x)≤f(x0)}上有下界，x0是初始点.

(ii)目标函数f(x)二次连续可微，它的梯度函数g(x)是Lipschitz连续，则存在常数L>0,使得：‖g(x)-g(y)‖≤L‖x-y‖,∀x,y∈N.

(iii)目标函数f(x)在Rn中是二阶连续可微的一致凸函数.

以下给出算法A的充分下降条件.在共轭梯度法的收敛性分析中，通常都有以下几个经典的引理，文中证明了相应的结果.

引理1.1假设{gk}和{dk}是由算法1产生的序列，则满足充分下降条件

1) 对∀k≥1，如果‖dk‖≠0,‖gk‖≠0，则有

(13)

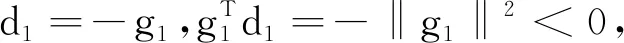
由(13)式得

于是有

综上，引理1.1得证.

(14)

证明：由式(12)和假设A得

(15)

将‖gk+1‖>3Lαk‖dk‖代入(15)式即得所要结论.

引理1.3若假设A成立，∀k>0,gk,dk≠0，则由算法1生成的序列{gk}和{dk}满足Zoutendjik条件

(16)

此外，由Lipschitz条件有 (gk+1-gk)Tdk≤αkL‖dk‖2.

以上2式结合得

(17)

(18)

即引理1.3成立

2 算法的全局收敛性

根据前面的引理部分，也能得到如下的收敛性证明.

证明：反证法，若结论不成立，就一定有常数ζ>0，满足任给k≥0,

‖gk‖≥ζ.

(19)

显然与引理1.3相矛盾，故定理2.1成立.

3 数值实验

本节中，为测试新方法的数值计算效果而建立数值实验，在强Wolfe线搜索下，文中的谱共轭梯度为记为PCSWP；在一般Wolfe线搜索下，建立共轭梯度法的数值实验，记为CWWP,分别与文献[16]的方法作对比，记为JPSWP法，测试问题选自文献[7]中的部分函数，算法的终止条件为‖gk‖≤10-6，或算法迭代次数超过 10 000，所有代码均在Matlab2016a中进行，数值结果以NI,NF,NG的形式给出，NI是算法迭代次数，NF是目标函数计算次数，NG是梯度函数计算次数，“*”指算法运行失效，经过各种尝试和严格的对比后，各参数的取值如下：PCSWP法中的参数μ=0.01,λ=0，CWWP法中参数μ=0.01,λ=0，而文献[16]中作者只是在Armijo线搜索下分析算法的全局收敛性，并未进行数值实验，故本文在强Wolfe线搜索下建立，且μ=1.1

各测试结果如表1：

表1 不同问题各算法测试结果表

续表1

从表格中可以看出，对于绝大部分测试问题，在强Wolfe线搜索下，本文提出的谱共轭梯度法(PCSWP)比文献[16]中的谱共轭梯度法(JPSWP)更有效，算法更具有竞争力，算法的迭代次数、目标函数的计算次数和梯度函数计算次数等方面均能达到最小.极少数测试问题上，求解GAUSS函数和WATSON函数时，JSWP法更有效；另外，本文在进行数值实验时，放宽线搜索条件，在一般Wolfe线搜索下，CWWP法比JSWP法和PCSWP法更有效；还有极少数问题，是无论选什么方法，测试结果都一样.综上，本文提出的谱共轭梯度法更有效，具有更好的数值性能.

4 结语