利用平均振动响应能量的螺栓松动检测方法

伍济钢,邵俊,周根,阳德强,成远

(1.湖南科技大学 机械设备健康维护湖南省重点实验室,湖南湘潭 411201;2.中国航发湖南南方宇航工业有限公司,湖南株洲 412002)

螺栓连接以其具有低成本、易于安装、承受负荷大等优点广泛应用于诸多工程领域[1]。同时,结构在工作过程中极易受到疲劳、冲击等载荷的影响而产生振动,长久振动可能会引起螺栓松动的产生,这将带来极大的安全隐患[2],因此,为了确保设备健康平稳运行,简单有效检测这些结构的螺栓松动故障至关重要[3]。

近年来,国内外众多学者所提出螺栓松动检测方法主要包括:阻抗法[4-6],振动法[7-9],超声法[10-12]。其中,振动法基于螺栓连接松动本质上是螺栓连接刚度减小,导致结构松动损伤后振动信息发生变化,可依据由松动损伤引起的结构动态参数变化或振动响应特征变化检测螺栓松动。He等[13]提出利用结构固有频率变化来检测螺栓连接的松动,并以带螺栓法兰的钢制管道结构为实验对象,成功地检测出了松动螺栓位置。Milanese等[14]使用光纤应变传感系统获得结构的应变响应数据,研究了两种从仅输出振动数据中检测松动方法,并通过螺栓连接梁实验验证了所提出方法的有效性。李允公等[15]考虑到螺栓松动会导致被联接件结合部动力参数发生变化,由此提出了一种基于两被联接件振动信号的松动识别方法。谢锋云等[16]针对螺栓出现松动故障信号产生非线性的现象,提出了一种基于VMD与LSSVM模型相结合的螺栓松动状态识别方法,并以2块15 mm厚的钢制螺栓连接板为实验对象验证了该方法的有效性。刘景良等[17]提出了一种基于归一化频响函数曲率差的钢-木组合梁螺栓松动定位方法,建立了钢-木组合梁有限元模型并进行了仿真分析,分析结果表明该方法能清晰地定位螺栓松动。

上述应用振动法进行螺栓松动检测的研究,主要依据螺栓松动损伤导致结构刚度变化,影响了结构动态特性参数(固有频率、阻尼等)和结构响应特征的原理进行松动损伤检测,而在螺栓松动损伤较小情况下,结构动态特性参数的变化并不十分明显。针对该问题,本文从振动响应能量的视角,在机理上解释了将平均振动响应能量作为螺栓松动损伤指标的合理性,提出利用螺栓松动前后该指标相对变化量构造损伤指数,并根据损伤指数大小判断松动螺栓所在位置。结果表明该方法能够简单有效的检测结构中的螺栓松动位置。

1 螺栓松动检测原理

根据频率响应函数定义可知,一个N自由度系统中激励点k与测量点i之间的频响函数Hik(ω)为[18]

(1)

式中:fk(ω)为k点输入激励;xi(ω)为测点i的响应;φir为i点的第r阶模态振型值;Kr、Mr和Cr分别为第r阶模态刚度、模态质量和模态阻尼。

由式(1)可以看出,频响函数幅值受到输出响应位置i的模态振型值φir与激励点位置k的模态振型值φkr的控制[19]。而模态振型通常可作为损伤检测的一个重要指标,基于此,可利用频响函数进行损伤检测。

式(1)可写为

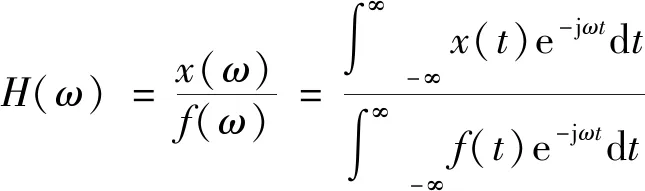
(2)

在实际应用中,由于输入激振力大小经常难以确定,文献[18]在不考虑输入激振力情况下,通过丢弃公式(2)中分母的方式,提出了基于加速度响应能量的损伤检测策略,并对大跨度斜拉桥损伤进行了分析。

基于以上思想,针对螺栓连接结构,可建立振动响应能量相关的螺栓松动损伤指标为

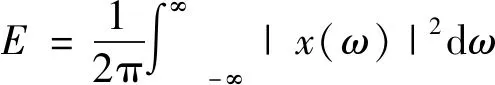
(3)

根据振动信号时域形式,式(3)螺栓松动损伤指标可以写为

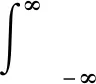
(4)

为减少噪声对数据结果的影响,通常需在相同环境下获取多组数据或者对一次采集获得的信号进行分段,其次对其进行平均处理以提高结果准确度,基于此,本文提出将平均振动响应能量E作为螺栓松动损伤指标,因此有

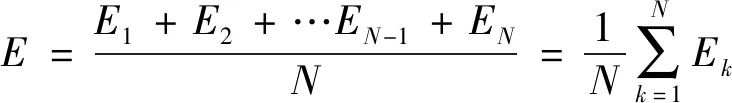
(5)

式中:N为分段数;Ek为第k段信号振动响应能量。

本文将螺栓松动前后平均振动响应能量E的相对差异程度定义为螺栓松动损伤指数δ,于是有

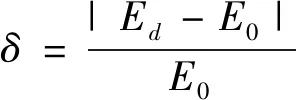
(6)

式中:E0为无松动(健康)状态下螺栓附近位置处的平均振动响应能量;Ed为松动后螺栓附近位置处的平均振动响应能量。

由公式(6)可以知道,螺栓松动损伤指数δ值越大,说明该螺栓松动前后的平均振动响应能量相对差异程度越大,即螺栓出现松动的可能性越大;而螺栓松动损伤指数δ值越小,说明该螺栓松动前后的平均振动响应能量相对差异程度越小,即螺栓出现松动的可能性越小,因此,可以找出最大松动损伤指数δmax对应螺栓即为松动螺栓。

2 利用视觉测量的振动响应能量获取

为方便获取各螺栓附近位置平均振动响应能量,提出利用视觉测量的振动响应能量获取方法。图1所示为单目视觉振动测量模型。a为像距,b为物距,O为相机镜头光心。假设A为静止时物体所在空间位置,B为静止时物体在成像平面投影位置。

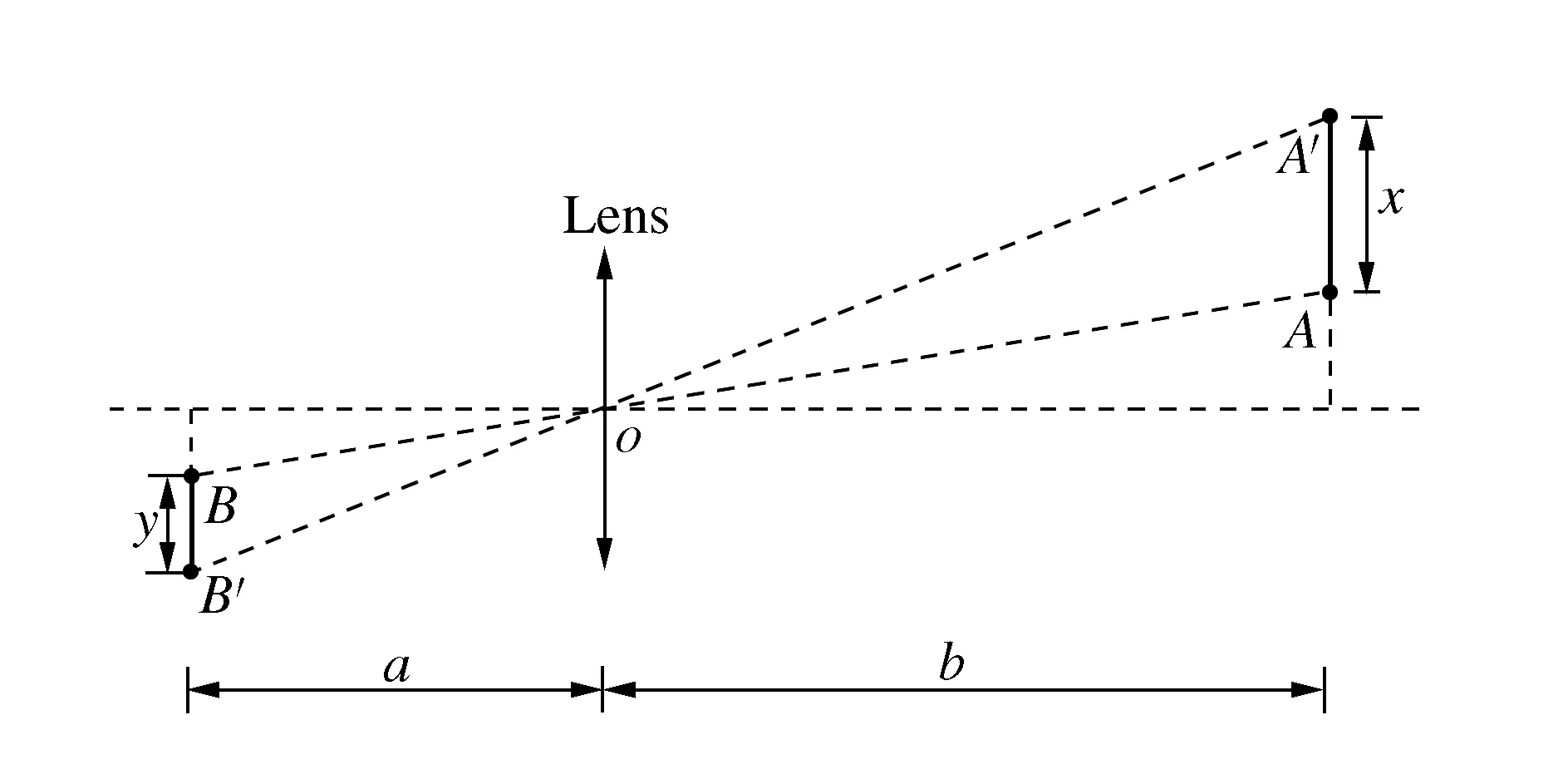
图1 单目视觉振动测量模型

如图1所示,假设物体运动方向平行于成像平面,当经过时间间隔kΔt后,物体在空间中由A点位置运动到A′,其空间中运动位移记为x,此时,物体在成像平面上投影位置则由B点运动到B′,其像素位移记为y。根据图1中相似三角形关系,可以得到

(7)

若以均匀时间间隔(Δt,2Δt,…,(N-1)Δt,NΔt),获取物体在空间中相对于静止位置时的振动信号为x(t),此时,物体在成像平面相对于静止时投影位置振动像素信号为y(t)。由此,根据式(7)可以得到

(8)

当相机和被测物体两者相对位置确定时,a与b均为常数,此时,由式(8)可知,物体在空间中实际振动位移x(t)与其投影在成像平面上像素位移y(t),两者成正比例关系,比例因子为b/a。

结合式(4)、式(5)和式(6)可知,该比例因子b/a在通过公式(6)计算螺栓松动损伤指数δ时将被约分,导致利用像素位移y(t)计算的螺栓松动损伤指数值与利用实际位移x(t)计算的损伤指数值大小相等,因此采用视觉测量方法获取其振动响应能量时,无需进行相机标定,可直接利用像素位移信号计算螺栓松动损伤指数δ。

3 利用平均振动响应能量的螺栓松动检测方法流程

基于以上分析,利用视觉测量方法获取其振动响应能量,提出一种利用平均振动响应能量的螺栓松动检测方法,图2所示为松动检测方法流程图。

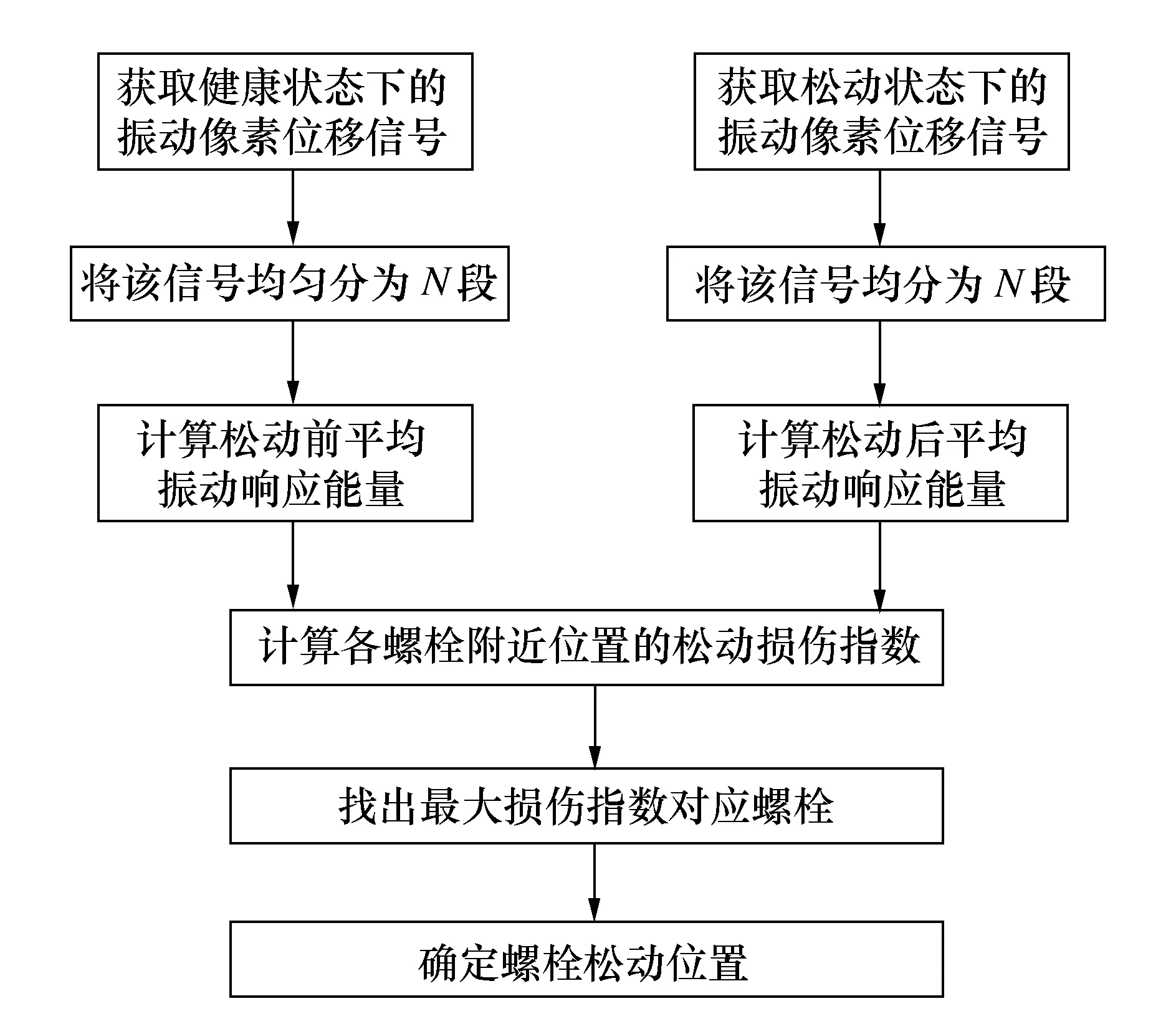
图2 松动检测方法流程图

具体步骤如下:

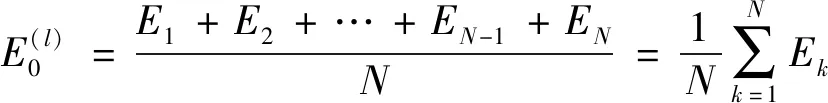
(9)

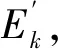
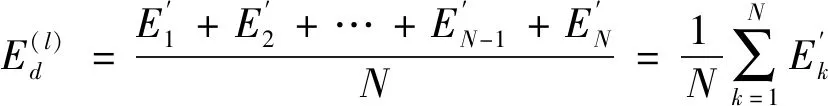
(10)

步骤3 利用松动前后各螺栓附近点的平均振动响应的能量,根据式(11)计算松动前后连接件上第l个螺栓附近点平均振动响应能量的相对差异程度(即螺栓松动损伤指数)。

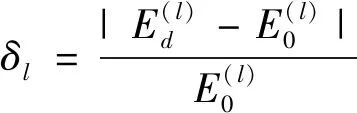
(11)

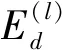
步骤4 重复以上步骤,计算所有螺栓平均振动响应能量相对差异程度δ值,找出最大松动损伤指数δl=max(δ1,δ2,…,δL)对应螺栓号l即为松动螺栓。

4 实验验证

为进一步验证本文所提出的螺栓松动检测方法的有效性,设计了图3所示的螺栓松动检测系统,最终搭建了图4所示螺栓松动检测实验平台。图5所示为激振器和螺栓连接板。

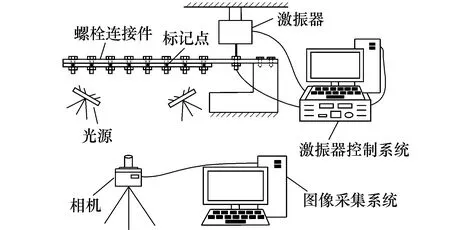
图3 螺栓松动检测系统

图4 螺栓松动检测实验平台

图5 激振器和螺栓连接板

该螺栓连接件由一块尺寸为777 mm×50 mm×2 mm铝制板与一块尺寸为510 mm×50 mm×2 mm铝制板通过10个M6×16螺栓连接而成,激振器通过顶杆与该螺栓连接件相连,工业相机通过三脚支架放置在合适位置。同时,通过预紧力矩大小调节螺栓紧固程度来模拟松动损伤,图4中右下方为所用的力矩扳手。该螺栓连接件上共10个螺栓,通过在连接件上各螺栓附近位置粘贴标记点建立醒目特征,标记点可记作bolt1,bolt2,…,bolt9,bolt10,图6所示为某帧局部图像上标记点检测位置。

图6 图像上标记点位置

为避免螺栓预紧力大小超过铝质连接件材料的屈服极限,实验中通过力矩扳手设置预紧力矩大小为3 Nm时,则认为该螺栓完全紧固,预紧力矩大小为0时为完全松动状态,预紧力矩大小为1.5 Nm时则认为其处于半松动状态。由于基于能量的松动损伤指数无需考虑输入激励的影响,因此采用随机激励方式分别对有无松动条件下的螺栓连接件进行激励。在该螺栓连接件振动过程中,通过帧率为300 fps的高速相机进行连续图像采集获得其振动序列图像数据,在此过程中无需进行相机标定。在获得各螺栓附近标记点振动序列图像数据后,运用光流法[20]对图像进行处理,以获得各标记点振动像素位移信号,将振动像素位移信号均分为3段,计算松动前后各螺栓附近标记点平均振动响应能量的相对差异程度。

4.1 bolt2螺栓松动检测实验分析

首先利用视觉测量系统获取未松动(健康)状态下的各特征点振动像素位移信号,并将振动信号均分为3段,根据公式(9)计算可获得各标记点的平均振动响应能量;然后将利用力矩扳手将bolt2预紧力矩设置为0(完全松动),其他螺栓预紧力矩大小为3 Nm,利用视觉测量系统获取bolt2松动状态下的各特征点振动像素位移信号,并将振动信号均分为3段,根据公式(10)计算可获得各标记点的平均振动响应能量;进而依据公式(11)计算可以获得图7所示螺栓松动损伤指数直方图。

图7 bolt2螺栓松动损伤指数直方图

从图7中可以看出,2号螺栓松动损伤指数δ最大,表明bolt2螺栓松动前后平均振动响应能量的相对变化程度相对较大,而其他螺栓松动前后平均振动响应能量的相对变化程度较小,进而可以判定bolt2存在松动,而实际模拟松动是通过将bolt2的预紧力矩大小调整为0来实现的,即利用本文方法检测结果与实际模拟的松动位置是相吻合的。

4.2 bolt5螺栓松动的检测实验分析

为了进一步验证本文方法检测结果的准确性,相应地,利用力矩扳手将bolt5预紧力矩设置为0(完全松动),其他螺栓预紧力矩大小为3 Nm,在利用视觉测量系统分别获取松动前后状态下的各特征点振动像素位移信号后,进而根据前文所述方法流程,同理可获得图8所示螺栓松动损伤指数直方图。

图8 bolt5螺栓松动损伤指数直方图

从图8中可以看出,5号螺栓松动损伤指数δ最大,表明bolt5螺栓松动前后平均振动响应能量的相对变化程度相对较大,而其他螺栓松动前后平均振动响应能量的相对变化程度较小,进而可以判定bolt5存在松动,而实际模拟松动是通过将bolt5的预紧力矩大小调整为0来实现的,即利用本文所提方法检测结果与实际模拟松动位置相吻合。

4.3 bolt8螺栓松动检测实验分析

同理,利用力矩扳手将bolt8预紧力矩设置为0(完全松动),其他螺栓预紧力矩大小为3 Nm。在利用视觉测量系统分别获取松动前后状态下的各特征点振动像素位移信号后,根据前文所述方法流程,进而可获得图9所示为螺栓松动损伤指数直方图。从图9中可以看出,8号螺栓松动损伤指数δ最大,表明bolt8螺栓松动前后平均振动响应能量的相对变化程度相对较大,而其他螺栓松动前后平均振动响应能量的相对变化程度较小,进而可以判定bolt8存在松动,而实际模拟松动是通过将bolt8预紧力矩大小调整为0来实现的,即利用本文方法检测结果与实际模拟松动位置是吻合的,所以,本文提出的松动检测方法能有效获得螺栓松动位置。

图9 bolt8螺栓松动损伤指数直方图

4.4 不同螺栓松动程度检测实验分析

为进一步研究不同螺栓松动程度与松动损伤指数之间的关系,通过将bolt5预紧力矩大小分别设置为0(完全松动)和1.5 Nm(半松动)来模拟bolt5的100%松动和50%松动,并利用前文搭建的实验平台分别进行了2次松动检测实验,最终根据前文所述方法流程,可获得图10所示不同松动程度的损伤指数关系图。

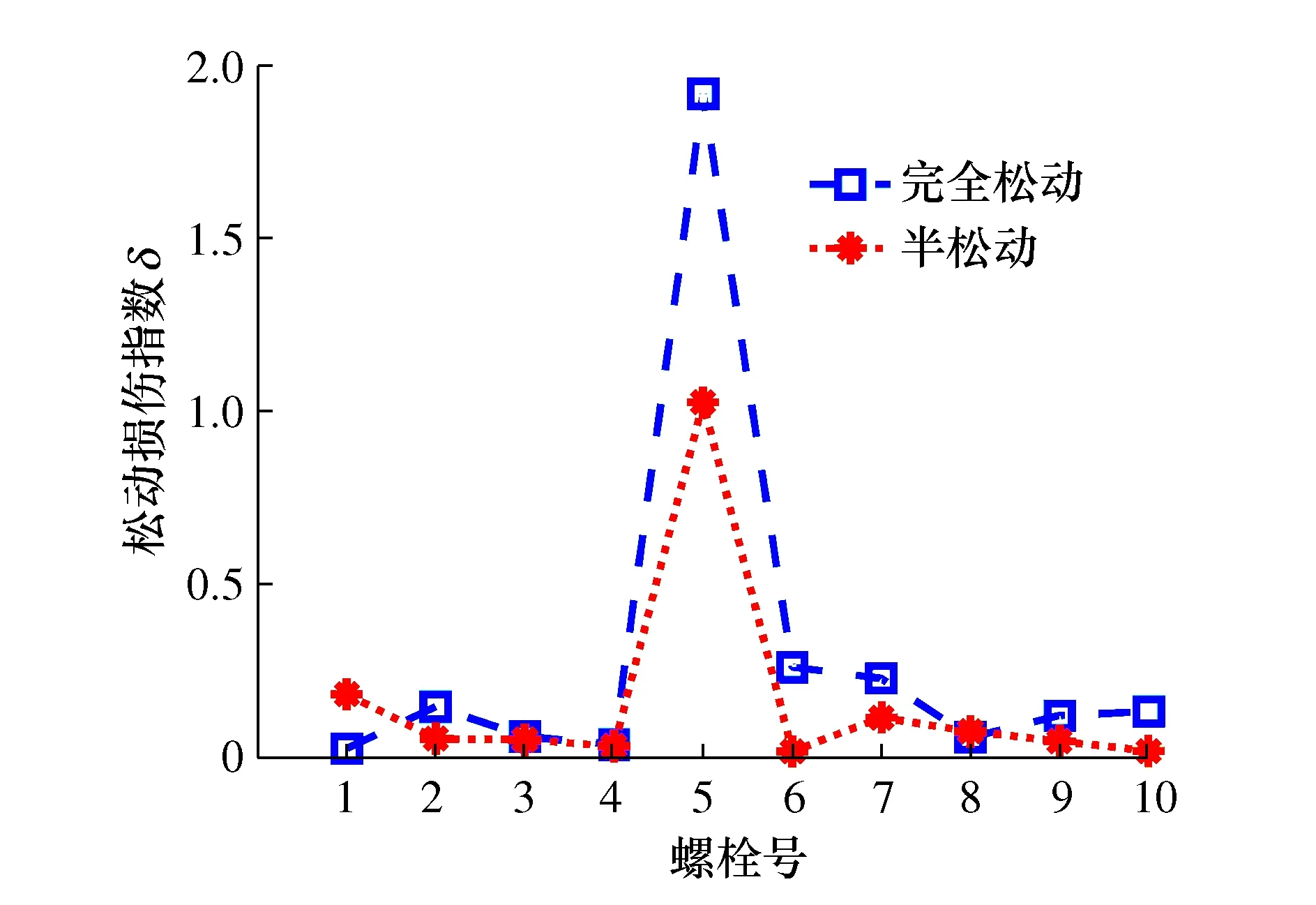
图10 不同松动程度的损伤指数关系

由图10可以看出,bolt5在完全松动状态下损伤指数值比半松动状态下损伤指数值大,原因是松动损伤指数代表螺栓松动前后平均振动响应能量的相对差异程度,bolt5完全松动状态下平均振动响应能量的相对差异程度比半松动状态下平均振动响应能量的相对差异程度更大。说明螺栓预紧力越小,松动程度越大,其振动响应能量的相对差异程度也就越大,损伤指数也越大。

5 结束语

本文提出了一种利用平均振动响应能量的螺栓松动检测方法,其计算方法为:采用视觉测量方法获取其振动响应能量,利用螺栓松动前后平均振动响应能量的相对变化量来构造损伤指数,并最终根据损伤指数大小判断松动螺栓所在位置。本文搭建了螺栓松动检测实验平台,并以螺栓连接板为实验对象,进行了螺栓松动检测实验,结果表明,该方法能够简单有效的检测结构中螺栓松动位置。需要说明的是,应用该方法进行多个松动螺栓的位置检测仍然需要进行下一步研究。