喷泉钟驾驭恒温晶振方法研究

肖娅聪，刘昆,*，刘洪康，房芳，陈伟亮，戴少阳，郑发松，李天初

(1.中国计量科学研究院，北京 100029；2.北京理工大学，北京 100081)

0 引言

冷原子喷泉钟[1]是一种基于激光冷却原子技术建立起来的频率基准装置。包含铯和铷两种工作介质。铯原子喷泉钟[2-4]是目前复现秒定义的频率基准装置，准确度和不确定度比使用热原子的前一代基准钟——铯束钟有了极大的提高。铷原子喷泉钟[5-8]有着碰撞频移小等优势，也被多家研究机构研制和应用。但另一方面，铯束钟[9]系统结构相对简单，能够连续不间断运行，独立输出标准频率，目前作为守时钟发挥着重大作用。作为基准钟使用的喷泉钟一般需要氢钟作为参考源，喷泉钟输出的是与该氢钟的相对频率偏差值，并驾驭氢钟形成标准时间[10]，但不输出标准频率。为了能够更好地利用原子喷泉钟，需要实现喷泉钟驾驭氢钟或者晶振，输出标准频率作为守时钟信号使用。这种驾驭的驾驭周期为几秒或者几十秒。美国海军天文台(USNO)实现了铷喷泉钟驾驭氢钟输出标准频率作为守时钟使用[11]，使得时标稳定度有了极大的提高。

1 算法原理

喷泉钟驾驭氢钟或者晶振等频率源的核心是根据历史数据预测下一个驾驭周期的频率平均值，并对频率源的频率进行调整。对于氢钟，频率调整需要通过相位微跃器[12-13]实现。对于恒温晶振，可以通过调整电压或者微跃器实现。喷泉钟数据是一种时间序列数据，关于时间序列的预测算法有很多种，包括移动平均法，简单指数平滑法，自回归平均移动模型(ARIMA)等。本文使用局部加权线性回归方法(locally weighted linear regression，LWLR)进行预测[14]，其他方法后续工作中再进行应用比较。

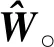
(1)

式(1)中，X为选出的自变量数据子集，Y为选出的因变量数据子集。W′为权重。LWLR使用“核”对附近的点赋予更高的权重。经常使用的核就是高斯核，高斯核对应的权重如下：

(2)

式(2)中，x为待预测自变量值，x(i)为选出的自变量数据子集中的值。由此构建一个只包含对角元素的权重矩阵W′，并且点x与x(i)距离越近，W′(x,i)值越大。式(2)中包含了一个用户指定的参数k，k控制权值变化的速率，k越大，离x越远权值下降越快。

(3)

2 数据模拟及比较

我们使用铯原子喷泉钟的真实数据进行模拟计算，先把每5个数值求个平均值，作为一个数据点，得到一个约为13 000个点的数据集，每个点代表7.5 s的相对频率偏差的平均值。计算时为了方便处理，舍弃时间信息，仅以点序号作为x轴。第2节所述计算中有两个可以自行设置的参数，式(2)中的k和参与计算数据长度N，计算结果表明当N>3k时，N增大几乎不影响预测结果。因此，固定N为100，k取1，3，10三个值，将预测结果比较，为了便于观察，我们选择i从1 000到1 100这段数据。图1为不同k值下预测值与实际值的比较，图中，黑色方点为喷泉钟实验数据，红色实线为k=1的预测值，蓝色虚线为k=3的预测值，绿色点划线为k=10的预测值。每个预测值都是由该预测值之前的100个点的数据计算出来的(序号在100点以内的预测值是由前面的所有数据计算得到)，通过比较发现，k=3时拟合适中。

图1 不同k值下的预测结果与实际数据比较

计算得到的预测值如果参与下一个驾驭周期的频率调整，理论上被驾驭的频率源就能跟喷泉钟实现锁频。衡量锁频效果的依据可以是预测值与实际值残差的Allan标准偏差。图2所示是不同k值下这个差值的Allan标准偏差值，图中黑色方点线为k=1的残差值的Allan标准偏差，红色圆点为k=3的残差值的Allan标准偏差，蓝色三角形点线为k=10的残差值的Allan标准偏差。从图2中我们可以看到k值越小，Allan标准偏差随时间增加下降得越快，也就说明被驾驭频率源能更好地和喷泉钟锁频。

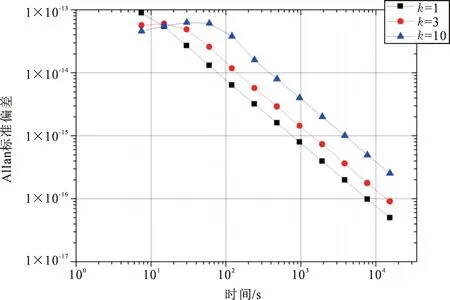
图2 不同k值下的预测值和实际值残差的Allan标准偏差

3 实验平台及结果

使用前文所述方法，选择k=3，N=100，将驾驭算法写进喷泉钟控制软件[15-16]中，驾驭周期选择每5个喷泉钟周期7.5 s，利用计算得到的预测值调整一次微跃器的输出频率。当喷泉钟的参考源是氢钟时，因为氢钟稳定度很好，驾驭效果要在天稳以上才能显现出来，并且测量时需要另外一台氢钟作参考，测量结果还受参考氢钟的影响。

为了能快速验证上述算法驾驭频率源的效果，我们搭建了如图3所示的实验平台。喷泉钟使用RAKON公司的HSO 14超稳恒温晶振作为参考源。我们先用计数器找到HSO 14输出5 MHz频率时的控制电压，并将该控制电压固定。5 MHz输出一路接到喷泉钟的频率综合器，生成9.192 GHz的激励微波信号，另一路接到SDI公司HROG-5RM微跃器的参考端。喷泉钟控制软件通过串口调整微跃器的频率输出，该频率输出即为驾驭后的频率。晶振的5 MHz输出为驾驭前的频率输出。

图3 实验平台

我们使用5125A测量系统测量这两个频率的稳定度，参考源用一台氢钟的标准频率输出，参考源氢钟的秒稳为5.4×10-14，百秒稳为3.5×10-15，万秒稳为3.2×10-16。测量结果如图4所示。从图中我们可以看出，驾驭前超稳恒温晶振因为存在频率漂移，秒稳虽然很好，为7.15×10-14，但中长期稳定度逐渐恶化。驾驭后频率漂移消失，中长期频率稳定度有极大的改善。实验结果表明该驾驭方法有效。

注：黑色方形对应自由运行的结果，红色圆形对应被驾驭后的结果

4 结语

本文引入局部加权线性回归为喷泉钟驾驭氢钟、恒温晶振等频率源的算法。先在理论上比较了不同参数下驾驭效果，然后搭建实验平台，改写喷泉钟控制程序，进行实验验证。结果表明，该驾驭算法有效，能够极大改善超稳恒温晶振的中长期稳定度。下一步将选择不同的驾驭方法进行实验验证，另外也将会把频率调整直接转移到改变超稳恒温晶振的控制电压上而不使用微跃器进行实验。