多极阱中汞离子数密度分布对二阶多普勒频移的影响

杨军，朱宏伟，刘志栋

(1.兰州空间技术物理研究所,兰州 730000;2.真空技术与物理重点实验室，兰州 730000)

0 引言

基于射频囚禁阱的离子微波钟在体积、稳定度、漂移率和可靠性等方面具有明显优势，已成为量子精密测量技术领域的一个研究热点。星载汞离子微波钟可具备气泡型铷原子钟的体积、主动型氢原子钟和磁选态铯原子钟的性能，以其优良性能和高可靠性，有望用于深空探测和下一代全球导航定位系统[1-2]。

目前，国内外有多家单位正在开展汞离子微波钟的相关研究工作，相较而言，美国JPL(Jet Propulsion Laboratory)喷气推进实验室[3-9]在汞离子微波钟的研制方面处于国际领先水平。2019年JPL实验室首次在国际上将汞离子微波钟发射到了太空，并开展了为期1年的深空原了钟(DSAC)任务演示验证实验，验证其单向导航的可操作性和有效性，经在轨数据分析表明：汞离子钟的在轨频率稳定度为(3～5)×10-15/1 d，频率漂移率为3.0(0.7)×10-16/1 d[9]。该汞离子钟在物理设计上采用四极阱与十六极阱相串联而成的两级分区式离子阱结构，实现了稳定囚禁汞离子和抑制二阶多普勒频移的目的。其中，四极阱用于离子制备和荧光探测等，十六极阱用于离子储存和微波作用，通过控制阱区间的电压可实现离子在两区间的穿梭运动。

关于这种设计的技术优势，JPL实验室[10]利用多极阱中离子数密度沿径向分布的物理模型，通过分析四极阱和十二极阱中离子云分布对二阶多普勒频移大小的影响而得出。该模型对于研究线型离子阱中离子云的规律，设计和优化用于离子钟的高性能离子阱有重要作用，国内中国科学院武汉物理与数学研究所[11]基于该模型开展了有关汞离子微波钟的研究工作。同时，该模型的运算量小，成本低，在基于多极阱的离子钟的先期研发阶段，可免去数值求解Mathieu动力学方程，尤其3D建模仿真(可采用Simion、Comsol软件等)带来的复杂要求[12-13]。

综上所述，尽管建立精确的多极阱中囚禁离子的动力方程或仿真模型，研究离子行为和优化阱机电参数更为直观，但采用离子数密度模型设计离子阱的途径，其性价比更高。本文在离子数密度分布模型基础上，进一步深入研究了多极阱中的离子云与空间电荷效应、二阶多普勒频移之间的关系。

1 多极阱中离子数密度的径向分布模型

对于由2k个电极构成的多极离子阱，囚禁质量为m，带电量为q的离子时，其阱内的电势场形式极为复杂，为简化引入赝电势并等效为[10]

(1)

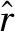
当阱中离子温度为T，径向总囚禁势为φ(r)时，径向离子数密度服从玻尔兹曼分布:

(2)

式(2)中,n(0)为阱中心轴线上的电荷密度，φ(r)=V*(r)+qφsc(r)为总囚禁电势，φsc(r)为空间电荷势,且由泊松方程描述为

(3)

研究表明，径向的离子数密度分布满足二阶微分方程[10]：

(4)

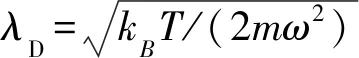
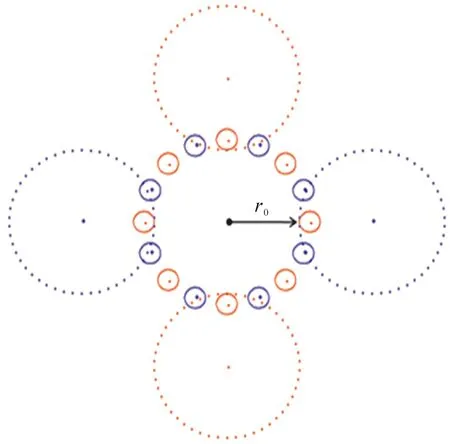
图1 四极阱与十六极阱结构图示

2 模型数值求解算法与计算程序

2.1 微分方程数值分析算法

对于如下初值问题的二阶微分方程

(5)

令y′=z后可化为一阶微分方程组

(6)

二阶微分方程可采用经典龙格-库塔法数值分析方法进行求解，其形式为

(7)

式(7)中：

(8)

令y=n(r),x=r,z=y′，二阶微分方程(4)将化为如下形式的一阶微分方程:

2014年，青海水利工作将深入贯彻党的十八大、十八届三中全会和青海省十二次党代会精神，紧紧围绕加快水利改革发展主线和提高服务保障能力主题，努力实现全省水利发展“投资规模有增长、发展速度有提升、管理水平有提高、体制机制有活力、行业建设有形象”五大目标，为建设新青海、创造新生活提供水利保障。

(9)

即方程组(6)中所述f(x,y,z)表达式为

(10)

考虑参数取值后，如图2所示，代入算法进行迭代计算即可求出n(r)。

图2 数值求解流程图

2.2 参数取值与计算程序

取k等于2、4、6和8，用于分析和讨论四极阱和多极阱中径向的离子数密度分布及其对二阶多普勒频移的影响。为使得研究具有参考性并保证离子稳定囚禁，主要离子囚禁参数取值如表1所示，同时引入绝热近似限制[10]:η<0.3。根据该模型成立条件，可推得对应Mathieu方程第一稳定区参数限制为：an=0,qn<0.3。在此基础上，给出了运算初始值，采用Matlab软件编程并运行了数值计算程序。

表1 离子囚禁参数取值

3 结果与讨论

3.1 离子囚禁参数对离子云的影响

根据表1参数取值，当取四极阱和多极阱中囚禁相同的离子数NL时(根据计算对应阱中心的离子数密度n(0)不同)，数值结果如图3所示。可以看出，随着电极数目2k的增加，离子阱中的离子云致密度逐渐降低，其中四极阱中的汞离子分布最为集中，而位于多极阱中的汞离子分布较为均匀。经分析，尽管两种阱的阱区半径相同，但造成这种现象的主要原因在于离子阱中的电势分布不同所致。如图示4所示，对比四极阱，多极阱内的势阱平缓且宽，并随着电极数目增加，多极阱产生的赝电势(图4(a))、空间电荷势(图4(b))和总囚禁电势(图4(c))的势阱深度逐渐变深，其宽度也逐渐变宽，结果离子云越来越分散，离子数密度不断降低。

图3 四极阱与多极阱中的离子数密度分布

图4 四极阱与多极阱中的电势分布

另外，从图4中发现四极阱和十六极阱具有相同的势阱深度，由于离子数密度和阱宽均不同，意味着后者具备囚禁更多离子数的能力。为此，取四极阱和多极阱在其阱中心的离子数密度相同，计算了相应的势阱深度和囚禁离子的数目，见图5所示。从图5可知，电极数目2k从4增加到16时，离子阱囚禁的相对离子数依次为1、1.57、1.98和2.28，而对应相对总势阱深度分别为1、0.43、0.62和0.98，这说明多极阱的势阱深度虽然没有四极阱的势阱深度深，但其具有囚禁更多离子的能力。例如，在上述参数设置中，十六极阱的势阱深度约等于四极阱的势阱深度，为0.98倍，但其囚禁离子的数目却是四极阱囚禁离子数目的2.28倍。

图5 四极阱与多极阱囚禁的离子数

从图4(b)和图4(c)中发现，空间电荷势对势阱的结构起到了一定的调制作用，而研究表明空间电荷势的大小与阱中囚禁离子的数目密切相关[5-6]。为了分析清楚离子数目对空间电荷势和离子云形态的影响机制，进一步在图3参数取值的基础上(即仍保持四极阱和多极阱中囚禁的离子数目相同)，只是将离子数扩大100倍，结果发现离子云形态发生了明显变化，主要现象如图6所示。可以看出，离子数密度分布与所示图3中囚禁较少离子数的情况不同:①尽管离子数增加导致离子云分布区域发生了变化，但四极阱中离子数密度分布曲线形态未发生变化，离子数密度最大的位置仍旧在离子阱中心位置；②囚禁离子数较多时，四极阱和多极阱中离子分布较为分散，这是由于当离子数增加时，离子间的库仑相互作用增强，即空间电荷效应明显，使离子向阱边缘汇聚所致；③多极阱中，其阱中心的离子数密度反而降低，靠近阱边缘区域的离子数密度增大，且表现出了离子数密度大于阱中心离子数密度的情况。对于产生第三种情形的原因，从图7(c)中可见，由于空间电荷效应，离子阱总囚禁电势底部发生了明显变化，沿着径向从阱中心到阱边缘，总囚禁电势分布呈现出先减后增的变化趋势，即在原有平缓势阱底部形成了一个小势阱(这与低离子密度时图4(c)中的情形不同)，结果离子大量汇聚在此处。图8给出了离子数密度峰值与总囚禁电势谷值之间的关系，其中离子数密度峰值对应图6，总囚禁电势谷值对应图7(c)，可以看出离子云峰值出现的位置恰好与总电势谷值出现的位置相对应。

图6 四极阱与多极阱中的离子数密度分布

图7 四极阱与多极阱中的电势分布

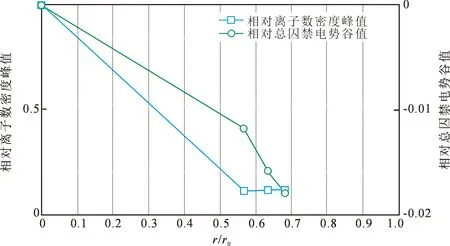
图8 离子数密度峰值与总囚禁电势谷值的位置对应关系

3.2 离子云对二阶多普勒频移的影响

对于汞离子微波钟，二阶多普勒效应是影响准确性的重要因素，由热运动和微运动等引起，在绝热近似条件下为

(11)

式(11)中，热运动引起的二阶多普勒项为

(12)

微运动引起的二阶多普勒项为

(13)

(14)

即总的二阶多普勒频移为[10]

(15)

图9 电极数对二阶多普勒频移的影响

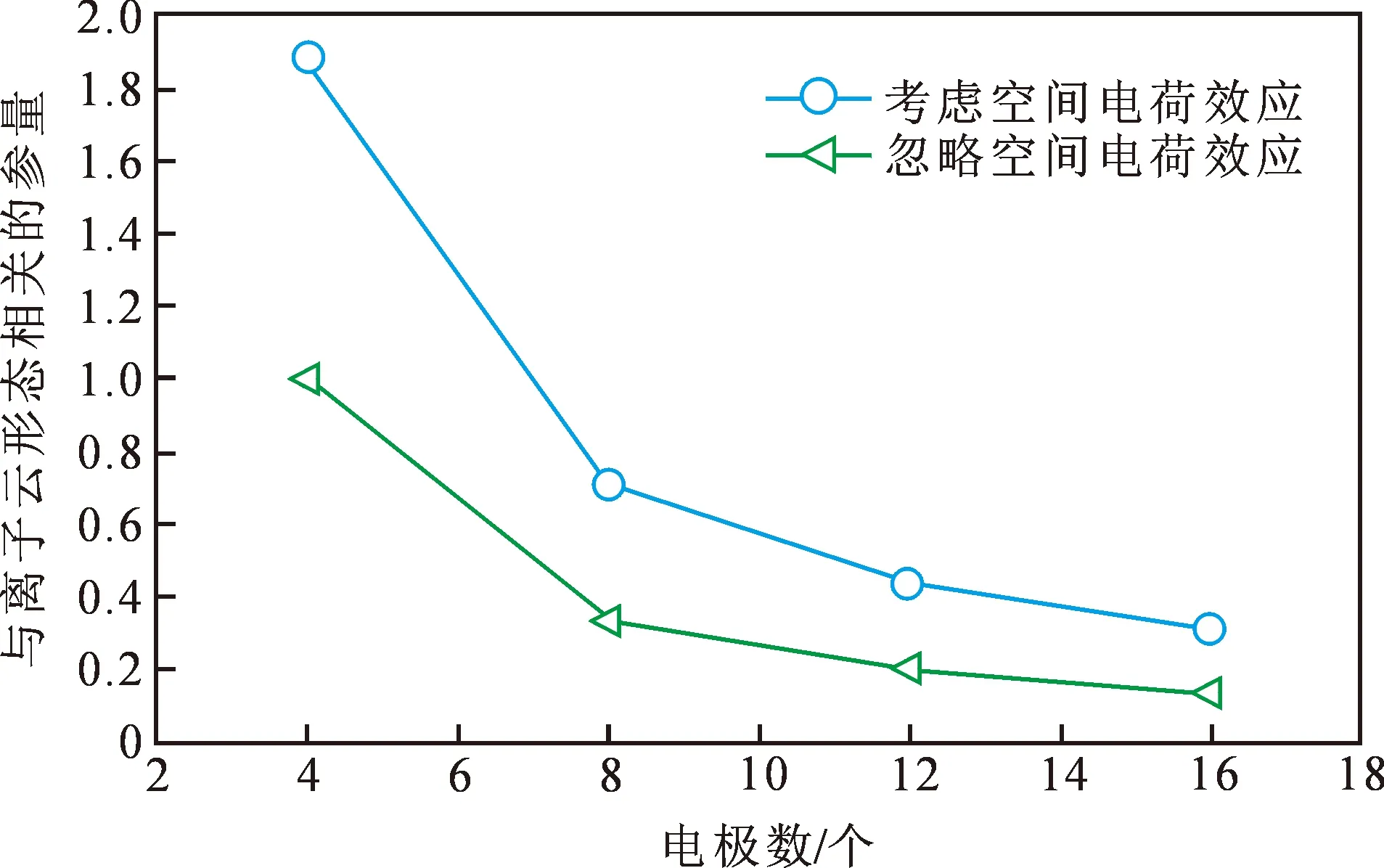
图10 电极数对离子云形态参量的影响

图11 离子数对二阶多普勒频移的影响

4 结语

在离子稳定囚禁条件下，基于线型多极阱中离子数密度沿径向分布的物理模型，研究了离子云的演变规律，比对了四极阱和多极阱囚禁汞离子的电势分布、空间电荷效应、离子微运动行为和二阶多普勒频移的异同。主要结论如下：

①四极阱中，势阱既深又窄，且阱中心囚禁电势最小，离子数密度沿着径向呈现出中心密而边缘疏的钟形曲线分布，离子分布在阱中较小区域内，空间电荷效应明显，离子微运动引起的二阶多普勒频移较大。

②对于多极阱，随着阱电极数目的增加，阱区内产生的有效势阱的深度增加，同时阱底部变宽，为离子在阱内分散囚禁，由阱中心至阱电极边缘，离子数分布较为均匀，从而降低空间电荷效应的影响创造了有利条件。此外，当阱中离子数密度较高时，空间电荷效应增强，离子空间电荷势的引入会改变多极阱势阱底部平坦的结构，总势阱底部沿着径向由阱中心至阱边缘出现了小势阱，两边高，中间低，导致离子数密度分布成两边疏中间密的分布形态。这种与四极阱的情况完全不同。

③根据文中算例，当四极阱和十六极阱势阱深度相同时，由于十六极阱的势阱较宽，可囚禁的汞离子数目较四极阱多，且离子分散分布，彼此库仑相互作用小，空间电荷效应导致的离子微运动较小，从而引起的二阶多普勒频移小于四极阱中离子微运动引起的二阶多普勒频移。

④无论是四极阱还是多极阱，当离子数目增加时，离子间的相互作用会增强，离子云在阱区径向分布更广，空间电荷效应明显导致二阶多普勒频移增大。若遇此情形，可考虑通过适当降低离子温度调节轴向电压等，减小热运动引起的二阶多普勒频移，使其接近或小于微运动引起的二阶多普勒频移的方法，从而降低二阶多普勒频移。