压电微动杆迟滞动力学建模与鲁棒控制研究

王海风， 冯兴伟， 李 青， 羊 毅， 潘枝峰

(1.中国飞行试验研究院，西安 710000； 2．中国航空工业集团公司洛阳电光设备研究所，河南 洛阳 471000； 3.西北工业大学，西安 710000)

0 引言

压电微动杆由于其高精度、高带宽、微位移输出特点，已成为现代光学设备主动调焦系统的关键部件，在各种高精度微位移输出机构中也得到了广泛应用[1-2]。然而，压电系统非线性迟滞效应严重限制了压电微动杆的控制精度，在非线性迟滞影响下，压电系统开环跟踪误差可达系统行程的10%～15%[3]。

为实现压电系统的高精度控制，国内外相关学者提出了各种迟滞动力学建模及补偿控制方法[4-5]。一般来说，压电迟滞模型主要包括物理模型和现象模型两类。物理模型包括Jile-Atherton模型和Maxwell模型[6]等，但由于其模型形式复杂，在压电系统建模和控制中较少使用。现象模型主要有Duhem模型[7]、Preisach模型[8]、Prandtl-Ishlinskii(PI)模型[9]和Bouc-Wen模型[10]等，这些模型直接采用数学方法对迟滞效应进行描述，具有更好的适应性，并已广泛应用于压电迟滞建模及控制研究。目前，压电系统控制多采用反馈控制[11]、前馈控制[12]或反馈-前馈复合控制[13]方法。然而，由于迟滞模型的复杂非线性特征，先进控制器的设计和实际应用较为困难，系统控制带宽受限。同时，在前馈补偿控制中，考虑迟滞逆模型精确求解及辨识的复杂性，系统的建模不确定性和参数敏感性会导致严重的补偿误差[14]。除此之外，上述多种迟滞模型并不适合描述压电系统的宽频带动力学特性，在高精度应用中，除考虑非线性迟滞影响外，还需要考虑蠕变[15]和机电动力学[16]等效应的影响。压电系统迟滞动力学精确建模及高精度控制仍需要进一步的研究。

本文以压电微动杆为研究对象，研究其多场迟滞动力学建模与鲁棒控制问题。采用多场建模理论，综合蠕变动力学、迟滞动力学及机电动力学模型，得到压电微动杆的多场迟滞动力学模型。同时设计一种鲁棒复合控制方法，通过鲁棒H∞反馈和逆Bouc-Wen前馈复合控制实现压电微动杆的高精度位移输出。其中，前馈控制基于逆Bouc-Wen模型，用于补偿非线性迟滞效应对系统精度的影响；鲁棒H∞控制器的设计依据非迟滞线性动力学部分，将迟滞部分作为建模不确定性处理以简化控制器设计，通过反馈控制补偿蠕变及机电动力学影响，提高系统控制带宽，在保证系统鲁棒性的同时进一步提高压电微动杆控制精度。最后，通过压电微动杆实验系统验证所建立迟滞动力学模型和所设计鲁棒复合控制方法的有效性。

1 压电微动杆迟滞动力学建模

1.1 压电微动杆

压电微动杆主要由压电作动器、菱形位移放大机构和连接杆组成，结构如图1所示。菱形微位移放大机构用来对压电作动器位移进行放大，保证压电微动杆作动行程。压电作动器沿菱形微位移放大机构长轴(y方向)放置，压电微动杆位移输出方向为x方向。

图1 压电微动杆结构Fig.1 Structure of piezoelectric micro-motion rod

在压电作动器两端施加一定电压，压电作动器运动引起的菱形微位移放大机构y方向伸长或缩短变形量记为δ0，相应地，压电微动杆沿x方向伸长或缩短变形量为δ，且有

δ=κδ0

(1)

式中，κ为菱形微位移放大机构的放大倍数。

1.2 压电微动杆迟滞动力学建模

压电微动杆系统具有机-电-热多场耦合特性，同时具有蠕变、压电迟滞等复杂非线性动力学特性。在高精度应用中，为实现压电微动杆精准位移输出，建立压电微动杆的多场耦合迟滞动力学模型，如图2所示。

图2 压电微动杆多场耦合迟滞动力学模型Fig.2 Multi-field coupling dynamic hysteresis model of piezoelectric micro-motion rod

压电微动杆的蠕变动力学效应可通过线性蠕变模型进行描述，即

(2)

式中：kc为常值增益；zci和pci分别为蠕变动力学模型零点、极点。

压电微动杆机电动力学模型Gev(s)分为电场动力学Ge(s)与机械动力学Gv(s)两部分分别进行建模，且有Gev=GeGv。其中，电场动力学主要包括RLC效应和RC效应，即

(3)

式中：τ为时间常数；C为常值增益；ωn1和ξn1分别为等效频率与阻尼。

压电微动杆等效机械模型如图3所示。

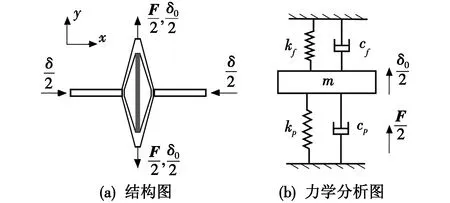
图3 压电微动杆等效机械动力学模型Fig.3 Equivalent mechanical dynamic model of piezoelectric micro-motion rod

图3中：kp，cp分别为压电作动器等效刚度和阻尼；kf，cf分别为菱形位移放大机构等效刚度和阻尼；δ0为压电驱动单元y方向作动位移；δ为压电微动杆x方向位移输出；F为压电作动器输出力作用。由图3可知，

压电微动杆机械动力学方程为

(4)

即可得压电微动杆机械动力学模型

(5)

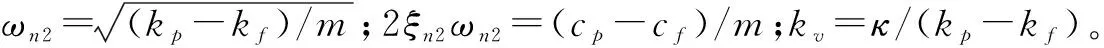
压电微动杆迟滞动力学部分采用Bouc-Wen模型进行描述，即

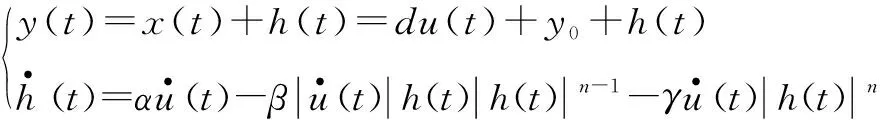
(6)

式中：y为压电微动杆输出信号；y0为初始输出偏差；u为电压输入；h为迟滞输出；d为比例系数；α,β,γ为模型参数；n为不敏感参数，本文中取n=1。

综合所建立蠕变、机电及Bouc-Wen迟滞模型即可得到压电微动杆的多场耦合非线性迟滞动力学模型。所建立模型具有明确的物理意义，从中可以得到一些典型的特征参数，如电动力学时间常数、振动动力学的共振频率及阻尼比等，对于压电微动杆系统的设计具有一定的指导作用。同时将线性部分与非线性迟滞部分分开建模，有利于先进控制器的设计。

2 压电微动杆动力学辨识

对1.2节中所建立的如图1所示压电微动杆动力学模型进行实验辨识。首先对压电微动杆的线性蠕变动力学模型进行辨识。选取周期为400 s的方波信号作为输入电压，采样时间间隔为10 ms。选取参数为na=4，nb=5和nc=4的ARMAX模型[17]辨识蠕变动力学模型，Gc的辨识结果可写成

(7)

机电动力学模型Gev的辨识选取周期为0.1 s的方波信号作为输入电压，采样时间间隔为0.1 ms。经过所辨识蠕变模型的逆模型，消除蠕变效应的影响。选取参数为na=7，nb=8和nc=7的ARMAX模型辨识机电动力学模型，Gev的辨识结果可写成

(8)

在压电微动杆Bouc-Wen迟滞模型辨识中，选取2组变幅值频信号u1(t)=10+10 sin 0.05 πtcos πt和u2(t)=15+10sin 0.05 πtcos πt作为压电微动杆电压输入信号，采样时间间隔为0.1 ms。经过所辨识蠕变动力学及电和振动动力学的逆模型，消除蠕变效应及电和振动动力学的影响。采用最小二乘法进行辨识，辨识结果为

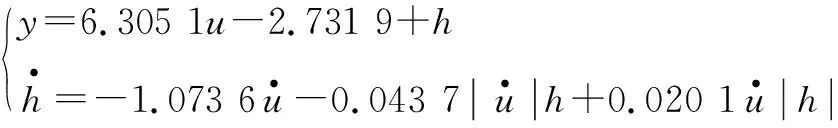
(9)

综合式(7)～(9)可得压电微动杆多场迟滞动力学模型。

3 压电微动杆鲁棒控制

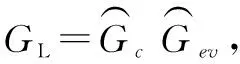
所设计鲁棒复合控制器框图如图 4所示。

图4 压电微动杆复合控制框图Fig.4 Compound controller of piezoelectric micro-motion rod

图4中w1为性能加权函数，在指定区间内保证控制性能，控制加权函数w2主要用来限制控制带宽和高频增益。此外，参考信号幅值选择参考信号加权函数wr，wu表示建模不确定性加权，系统不确定性为

δu=(1+Δuwu)

(10)

式中：Δu表示单位不确定，且‖Δu‖≤1;wu的取值根据Bouc-Wen迟滞输出占比确定。

鲁棒H∞反馈控制器设计采用回路整形技术，所设计加权函数为

(11)

根据所设计加权函数，通过DK迭代法求解得到鲁棒H∞控制器结构参数，所设计鲁棒H∞控制器的Bode图如图 5所示。

图5 鲁棒H∞控制器Bode图Fig.5 Bode plot of robust H∞controller

4 压电微动杆鲁棒控制实验研究

4.1 压电微动杆实验设备

为验证所建立压电微动杆多场耦合非线性迟滞动力学模型及所设计鲁棒控制方法，采用图1所示压电微动杆，搭建如图 6所示实验系统，主要包括压电微动杆、电涡流传感器及其信号调制器、dSPACE实时控制系统和上位机。

图6 压电微动杆实验系统Fig.6 Experimental system of piezoelectric micro-motion rod

实验中，电涡流传感器型号为美国雄狮公司的ECL150 U18 Probe，其量程为5 mm，有效分辨率为340 nm。电压放大器型号为E-500.621，电压放大倍数为10，输入电压范围-2～12 V。所采用压电驱动装置型号为CEDRAT公司的APA1000L，其最大行程为1058 μm，分辨率为9 nm。

压电微动杆实验系统如图 7所示。压电微动杆输出位移通过电涡流传感器进行测量作为反馈信号，通过dSPACE实时控制系统主动控制产生控制电压，经电压放大器放大从而对压电微动杆进行控制。

图7 压电微动杆实验系统框图Fig.7 Diagram of piezoelectric micro-motion rod experiment system

4.2 压电微动杆实验结果

为验证所设计鲁棒复合控制器的有效性，以下分别给出压电微动杆对不同类型参考信号的跟踪实验结果。同时，采用Z-N整定法设计比例-积分(PI)控制器，给出压电微动杆PI控制实验结果作为比较。实验中，压电微动杆的跟踪性能通过跟踪误差均方根进行评估，误差均方根算式为

(12)

式中,N为采样数。

图8和图9分别为采用PI控制和鲁棒复合控制时压电微动杆对幅值为200 μm、频率为1 Hz的正弦信号的跟踪结果及误差分析。由实验结果可知，跟踪误差均方根分别为2.84 μm和1.27 μm，鲁棒复合控制器相比于PI控制器跟踪误差减小了55.3%。

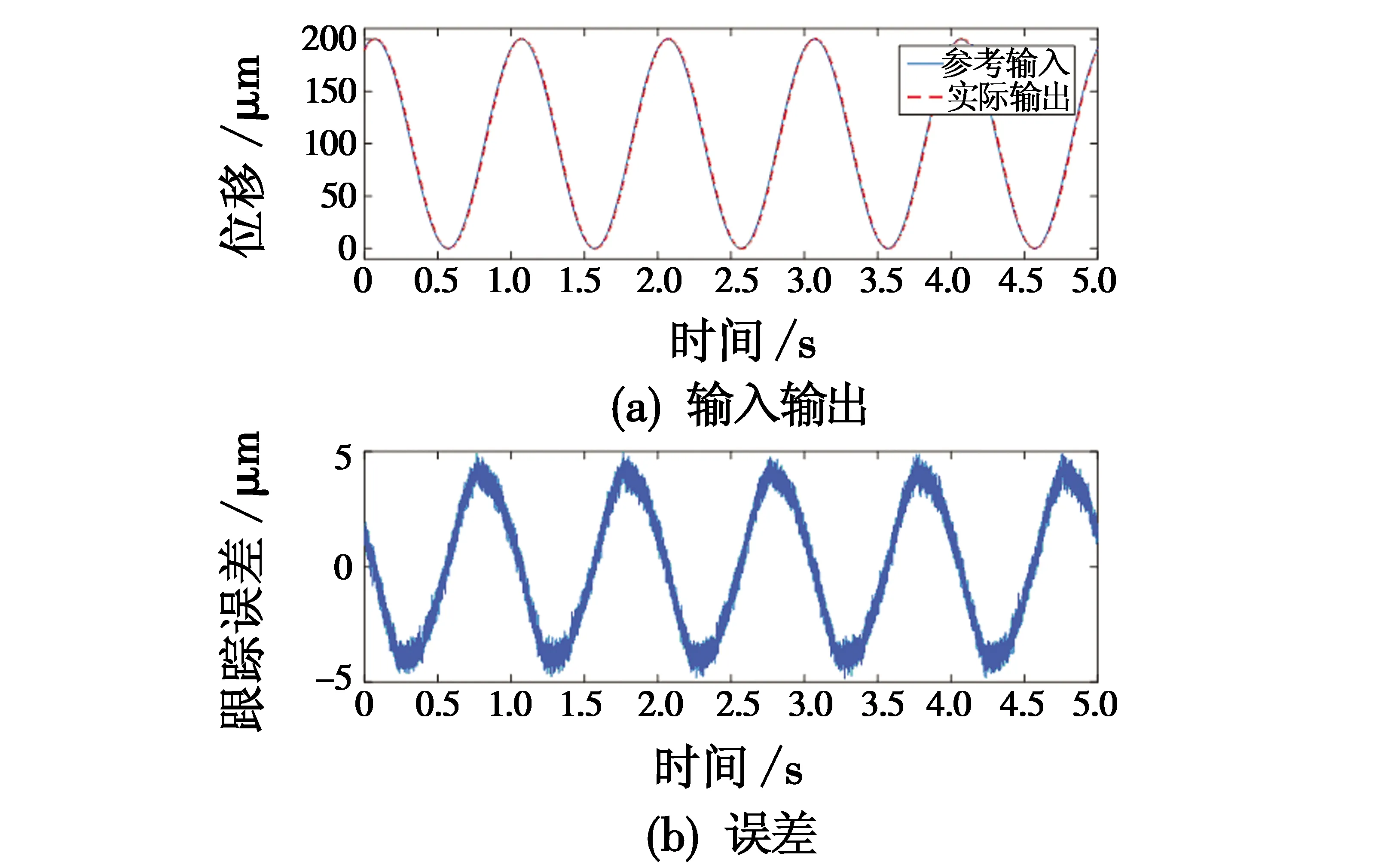
图8 正弦信号跟踪结果(PI控制)Fig.8 Tracking result of sine signal (using PI controller)

图9 正弦信号跟踪结果(鲁棒复合控制)Fig.9 Tracking result of sine signal(using robust compound controller)

图10和图11分别为采用PI控制和鲁棒复合控制时压电微动杆对幅值为200 μm、频率为1 Hz三角波信号的跟踪结果及误差分析。

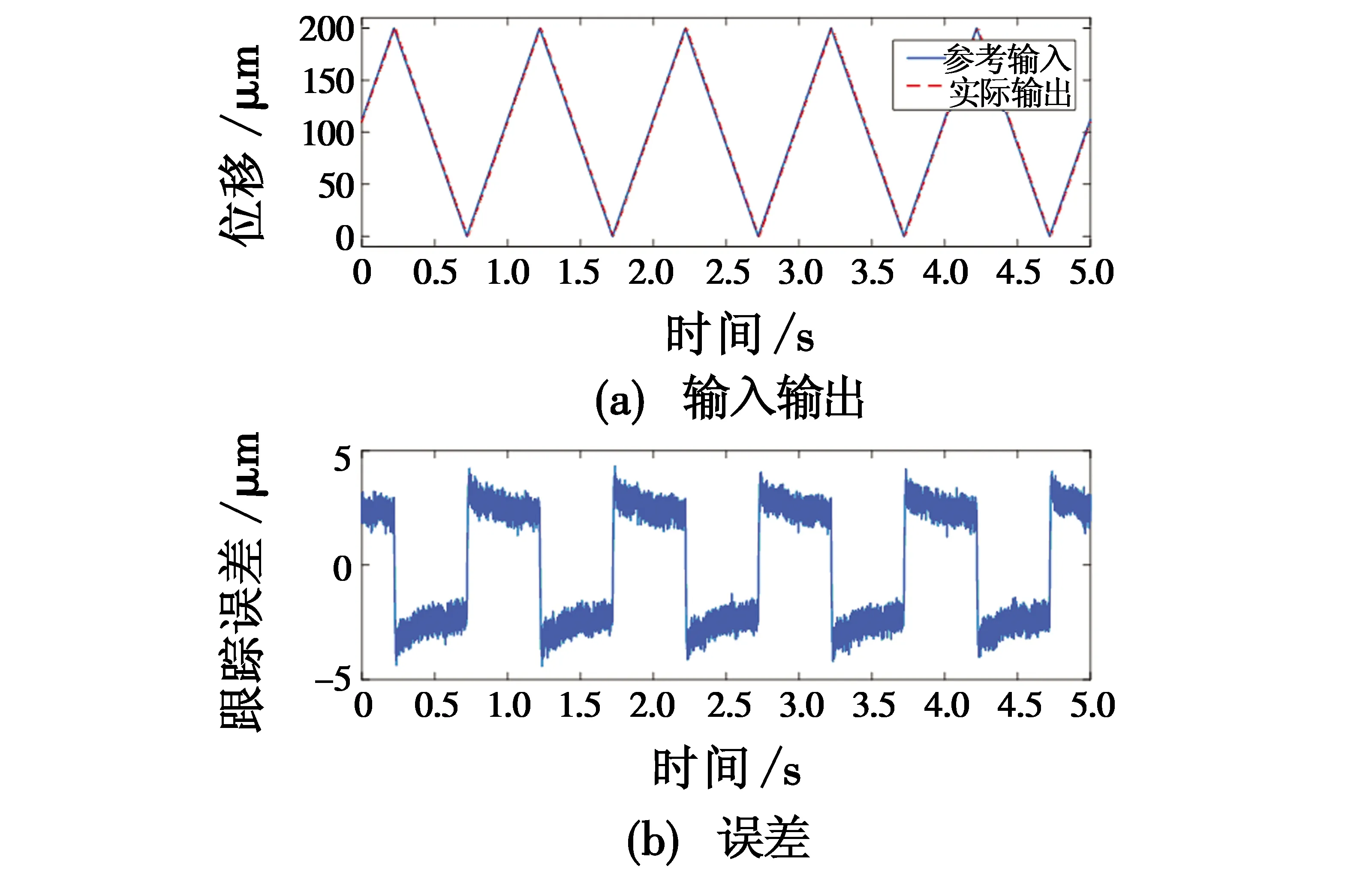
图10 三角波信号跟踪结果(PI控制)Fig.10 Tracking result of triangular wave signal (using PI controller)

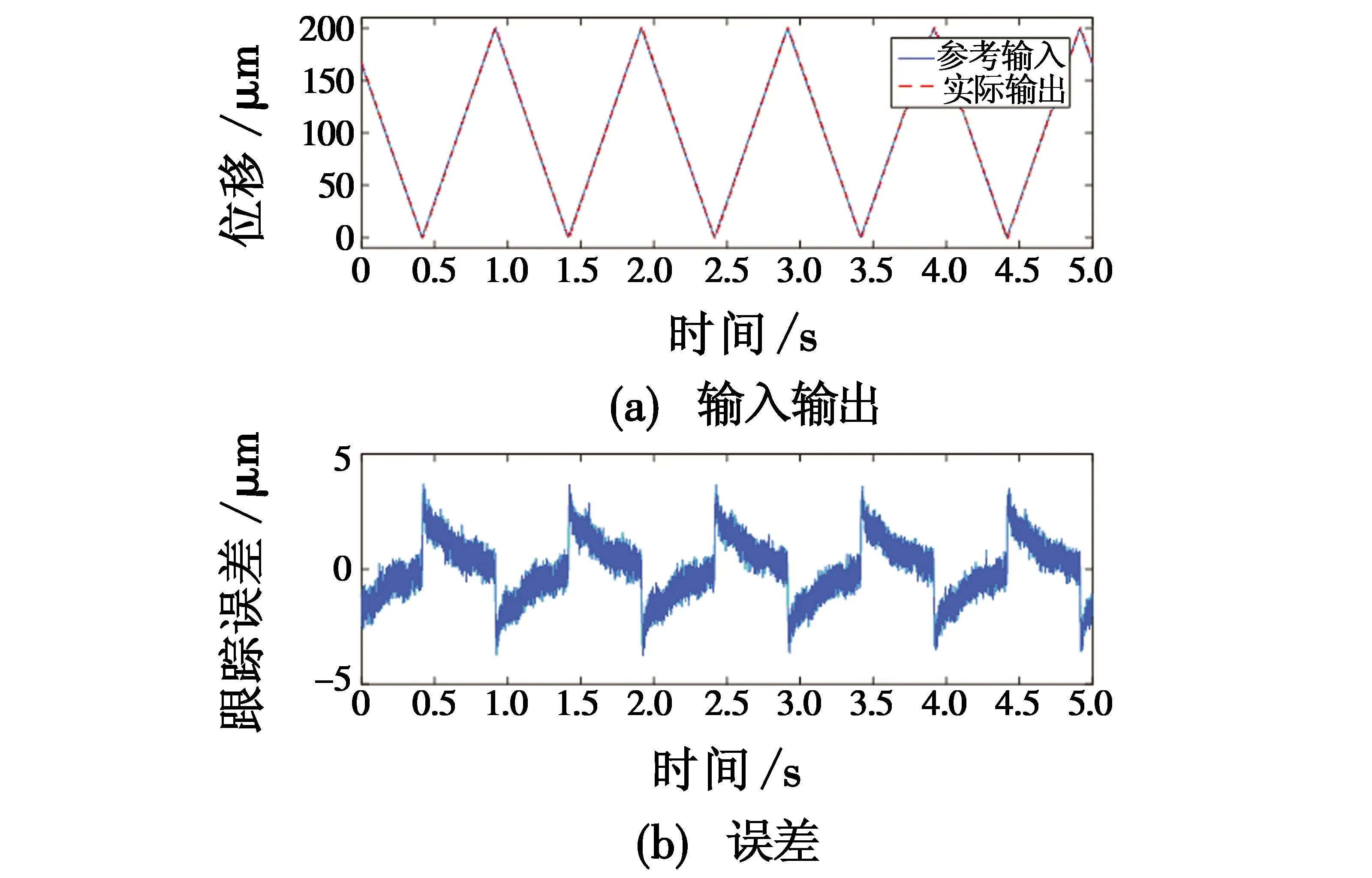
图11 三角波信号跟踪结果(鲁棒复合控制)Fig.11 Tracking result of triangular wave signal (using robust compound controller)

由实验结果可知，跟踪误差均方根分别为2.60 μm和1.25 μm，鲁棒复合控制器相比于PI控制器跟踪误差减小了51.9%。

从以上实验结果可看出，所设计鲁棒复合控制方法能够实现更好的控制性能。考虑压电微动杆跟踪信号的多样性，为进一步验证所设计鲁棒复合控制器的有效性，采用正弦、方波及三角波3种信号组成的复合信号作为压电微动杆参考输入信号，如图12所示。

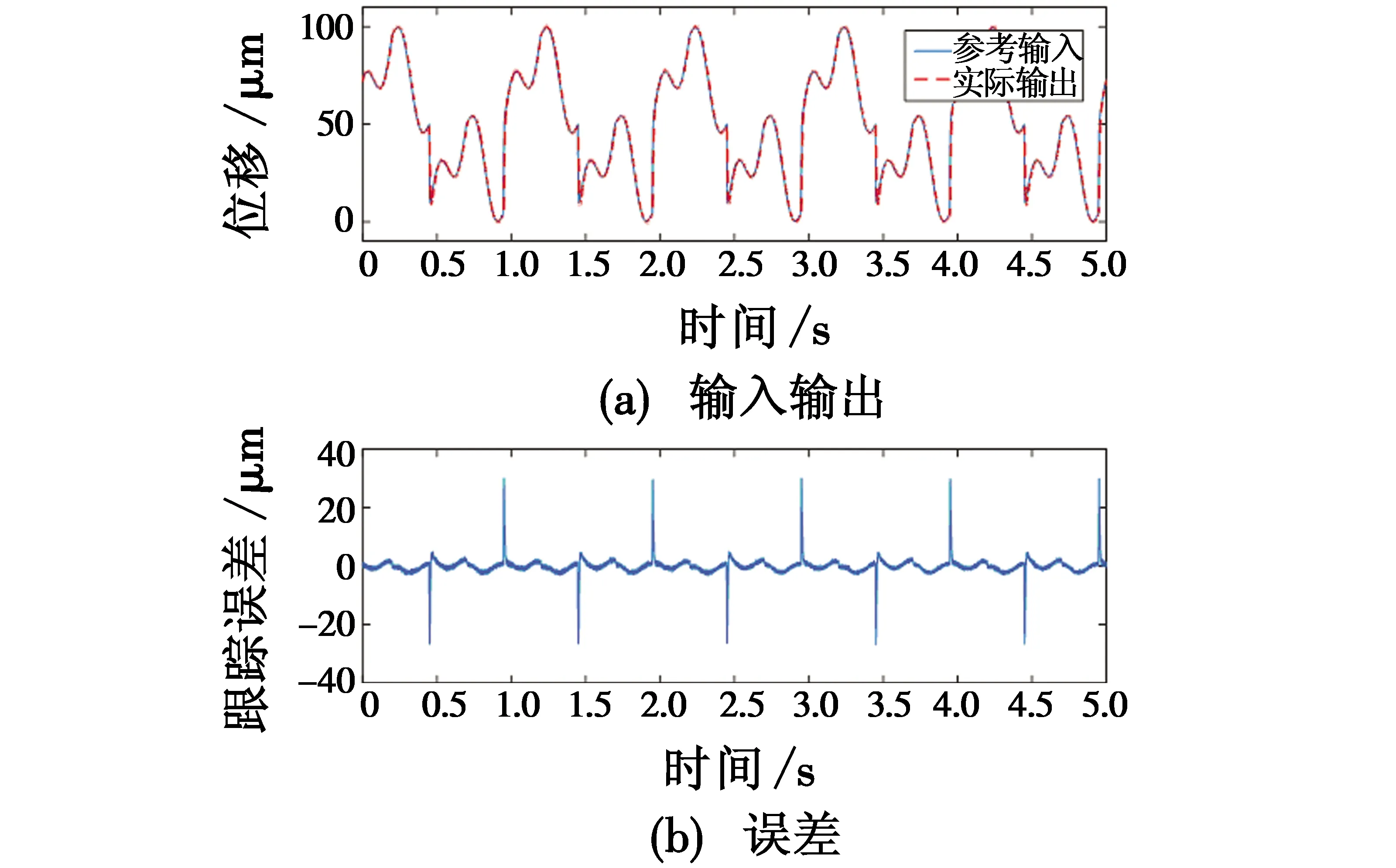
图12 复合信号跟踪(鲁棒复合控制)Fig.12 Tracking result of compound signal (using robust compound controller)

由图12实验结果可知，跟踪误差均方根为3.0 μm。

5 总结

本文以压电微动杆为对象，研究了其迟滞动力学建模及鲁棒控制问题。采用多场建模理论，建立了压电微动杆的精确动力学模型并给出参数辨识过程。同时设计了一种鲁棒复合控制方法，在保证系统鲁棒性的基础上实现压电微动杆的高精度控制。实验结果表明，所设计鲁棒复合控制方法能够实现压电微动杆的高精度控制。本文所设计压电迟滞动力学建模及鲁棒控制方法可以应用于光学主动调焦、微定位等高精度位移控制应用场景。