基于剖分网格改进A*算法的航迹规划研究

陈晓宏， 储飞黄， 方胜良， 马 昭

(航天工程大学，北京 101000)

0 引言

以上文献都有以算法运行效率为目标的问题，在栅格环境中尝试了算法融合或改进启发式搜索函数的方式对A*算法进行改进，但都未尝试对栅格环境的空间底层表征做出改变后改进算法。为从底层空间表征着手，本文尝试结合网格组织的立体空间剖分网格理论，利用剖分网格中的“编码-空间-信息”一一对应的空间表达能力以及剖分编码的八叉树层级结构特点，改进g(n)求解方式使之在路径寻优中更加具有指向性优势，减小算法的搜索空间。然后将任务区域分段划分，采取变步长的策略进行航迹规划，使航迹能在贴合作战实际的同时节约计算资源，高效运行。

1 相关理论

1.1 空间网格剖分理论

图1所示为剖分网格组织方式。全球多尺度剖分网格框架[12]GeoSOT(Geographic coordinate Subdividing grid with One dimension integral coding on 2n-Tree)以赤道与本初子午线交点为中心，将地球拓展为512°×512°的0级网格，并按照八叉树结构不断向下细分至32层级。而后按照图2所示结构，分层级编码形成了“编码-空间-信息”一一对应的八进制一维编码表达模型[13]。同时，因为在算法变步长设计时考虑的是相层级网格，且任务背景所占空域在整个剖分空间中所占比例较小，距离地心较远，本文对此选定空域的网格曲率不做进一步考虑，假设每一层级的网格大小相同且均为长方体。

图 1 剖分网格组织方式Fig.1 Organization mode of subdivision grid

图 2 剖分编码划分结构Fig.2 Split coding partition structure

1.2 基于栅格环境的A*算法

在寻路算法中栅格环境是较为通用的环境建模方式[14-16]。为与原算法对比，本文采用平面八向栅格图，即允许斜飞路径存在。在不考虑转向角等因素的约束下假设直飞相邻网格的实际移动代价为10 km，斜飞为14 km。

A*算法是启发式搜索算法，用于静态环境中的全局路径寻优问题，该算法需要建立open表和close表，open表存储父节点和子节点的f(n)值，close表存储open表中f(n)最小值构成的路径规划点。以平面直角坐标系为例，A*算法包含以下几个步骤：1) 将起点放入close表;2) 将起点作为父节点，并对周围8个子节点的f(n)值进行计算放入open表;3) 在open表中按f(n)值进行排序，选出f(n)最小值对应坐标放入close表；4) 将新放入close表的节点作为父节点重复步骤2)直至到达终点；5) 将close表中的规划点，从终点开始反向搜索子节点并形成最终路径。

A*算法的代价算式为

f(n)=g(n)+h(n)

(1)

式中:f(n)为总的路径代价值;g(n)为所规划路径由起点到当前点n所花费的实际移动路径代价值;h(n)为启发函数，代表当前节点n到终点的预计花费代价值，h(n)依据曼哈顿距离求解，即当前点到目标点的二维坐标差值乘以10，其算式为

由于会展旅游属于一种新生的旅游产品，所以相关的管理制度还不健全。这种情况下，会展旅游业的市场容易产生无序、紊乱的现象，影响行业的整体发展。即使成都市政府成立了专门的会展管理机构，但是由于管理制度的不健全，仍然缺乏对会展旅游业从业人员和办会单位的资质审查，导致大量水平低下、浪费资源的低水平会展重复举办，更有甚者，某些冒用政府名号举办的销售劣质产品的会展或者打着车展、漫画展等的名号举办的有伤风化的展会也得到审批通过，在社会上给会展旅游业造成了极大的负面影响。

h(n)=10×|xgoal-xi|+10×|ygoal-yi|

(2)

式中：xgoal与ygoal分别为目标位置的横、纵坐标；xi与yi分别为当前点的横、纵坐标。

2 基于剖分编码改进的A*算法

2.1 结合剖分编码特性的改进方式

剖分编码具有空间八叉树组织结构及平面四叉树组织结构两种类型，空间八叉树编码是基于二维平面增加高度维后的三维编码，两者基本原理相同，为方便和平面栅格环境中的A*算法对比，在介绍和对比分析本文A*算法改进方式时以平面四叉树组织结构为例。

2.1.1 实际移动路径代价惩罚因子p的建立

剖分网格在平面栅格环境中采用四叉树结构进行组织，内含了不同网格间的位置关系。基于该特点，可确定当前点与目标点同时存在的最小四叉树网格。利用如图2(b)中下层的0，1，2，3编码值对应位置关系可确定当前点通往目标点的直线最优方向。通过该指向方式可以迅速确定目标方位，而后通过图2所示方式确定惩罚因子p,并依据

f(n)=p×g(n)+h(n)

(3)

确定当前点n的总的代价值f(n),从而使飞行器在移动过程中的可行航迹寻找能力增强，节约计算时间。

图3所示为g(n)惩罚因子施加方式。

图 3 g(n)惩罚因子施加方式Fig.3 Penalty factor application method of g(n)

从图3实际移动路径代价最终值计算方式可以看出，通过四叉树结构寻找到目标所在方向后，将可行空间划为一线两三角的排列。若为直飞方向则改为三条线划分，惩罚因子相应值不变，对应施加位置改变。

2.1.2 分段变步长航迹规划

图4所示为平面栅格环境分段变步长编码位比较位置。设与飞行器速度、转向角等条件相适应的最小粒度网格层级的剖分编码共m位。

图 4 平面栅格环境分段变步长编码位比较位置Fig.4 Comparison position of coding bit of segmented variable step size in flat grid environment

因空间曲率及突防任务雷达威胁分布特点影响，设定判断距离D值将飞行器的全局飞行航迹规划分为巡航段和突防段，并且将变步长操作限制在两个相邻网格层级内变化。在h(n)值小于D值时，认为飞行器进入雷达威胁分布集中的突防段，此时采用小步长网格，即在剖分编码的位比较中比较到n(n能整除2)位，实现更精准的突防航迹点确定；在h(n)大于D值时，认为雷达进入雷达威胁分布较为稀疏的巡航段飞行，采用大步长网格，比较到n-2位。通过该方式可以节约全局路径规划的计算资源，同时也能保证目标突防进攻的有效性和航迹合理性。

2.2 改进A*算法逻辑结构

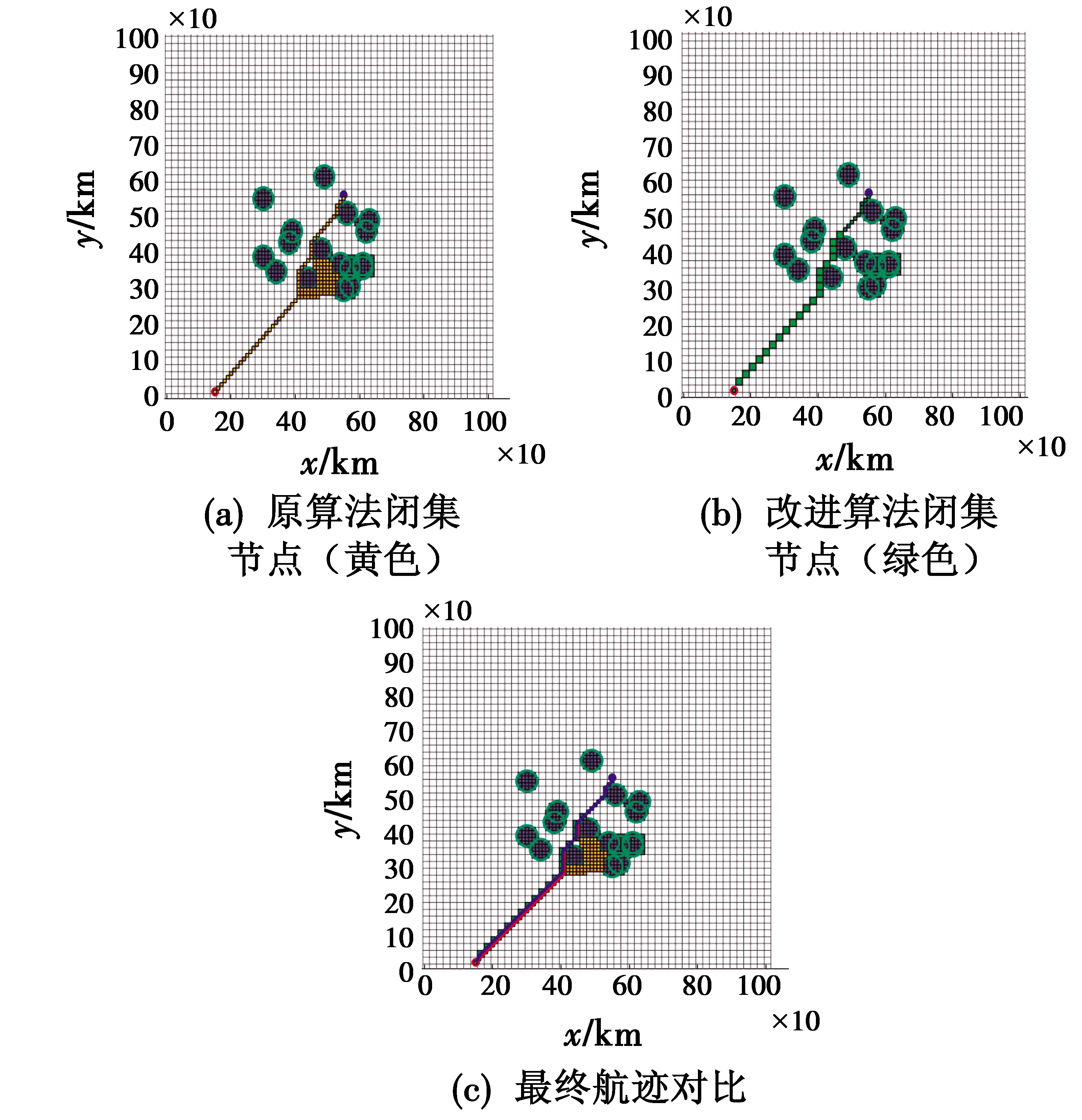
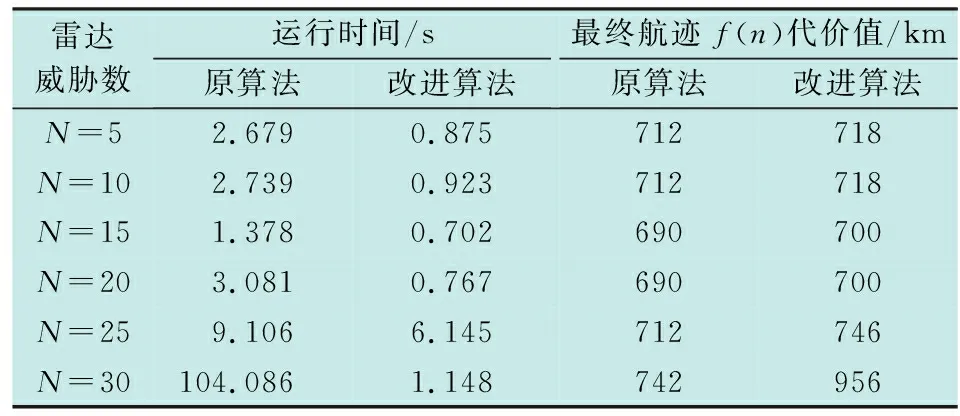
结合2.1节的设计策略，在适应飞行器的剖分网格环境建模基础上，其主要算法逻辑结构如图5所示。该算法在原有算法结构基础上增加了方向和距离判断环节，而后依据当前位置与目标位置的方位关系对g(n)施加惩罚因子p，使之在可行航迹寻找中更具指向性。变步长逻辑实现则是利用h(n)值与常数D的值进行比较，当h(n)≥D时，保持编码比较位不变，当h(n)

图 5 改进算法实现逻辑Fig.5 Implementation logic of the improved algorithm

2.3 性能分析

改进算法在寻找最优路径的同时，主要通过待计算节点的减少实现计算效率的提升，这体现在两方面：1) 利用惩罚因子使可行子节点的拓展偏向于目标方向，减少了计算节点；2) 将突防任务依据任务特点分成两段，在远距离采用高一层级网格相较于原算法可以减少3个计算节点的拓展，有效提高了搜索速度。

图6所示为栅格环境下雷达威胁建模的场景。假设网格间距为10 km，在整个空间中随机分布有20个最大探测距离(以探测概率值大于0.1为标准换算得到)为30 km的地基雷达，其联合分布用灰色网格表示，设为禁飞区。

图 6 雷达威胁分布示意Fig.6 Diagram of radar threat distribution

在图6环境建模基础上，算法计算节点对比实现效果如图7所示。由图7(b)中可见，改进算法的计算节点(绿色)少于图7(a)中原算法计算节点(黄色)，并且图7(c)中两者最终的航迹基本相同，f(n)代价值都约为690 km，但在运行时间上，原算法为14.231 s，改进算法为0.747 s，显著提高了突防任务背景下的航迹寻优效率。

图7 两种算法计算节点对比Fig.7 Comparison of calculation node of two algorithms

为进一步分析飞行器突防背景下环境复杂度对算法效率的影响，以随机分布的雷达威胁数(N=5，10，15，20，25，30)对最终航迹f(n)代价值和算法运行时间进行对比，最终结果如表1所示。可以发现，在环境越来越复杂的情况下，改进算法的效率和结果稳定性显著提升，更加适应突防任务中的雷达威胁分布密集背景。需要注意的是N=30的情况，当雷达威胁分布过于集中时，原算法无法寻找到最优路径或耗费时间极长，而改进算法总能良好地适应各类密集威胁环境。

表 1 环境复杂度对算法效能的影响对比Table 1 Comparison of the impact of environmental complexity on algorithm performance

经平面四叉树栅格环境下的算法对比分析可知，利用剖分编码对空间进行表征并结合该特点改进A*算法后，算法性能提升，计算节点减少，提高了运行效率，更能适应突防任务雷达威胁集中的环境特点。

3 立体空间剖分网格算法结合应用

为在立体空间中展现改进算法的结合应用能力，利用Cesium平台，基于以下软硬件配置进行仿真：硬件环境为微型计算机1台(处理器：Intel®CoreTMi7-9700CPU@3.00 GHz；内存:32.00 GiB)。软件环境为64位Windows10操作系统； Cesium1.76版；Google Chrome浏览器为64位最新版。

3.1 条件假设设置

本文基于以下3个假设对飞行器和雷达威胁进行设置。

假设1(剖分网格层级确定) 假设飞行器在等时间步长T、以速度V匀速飞行，V×T得到的距离值为网格大小比较值，寻找相应的最小兼容网格边长为最小层级L，向上兼容。l代表相应层级标准网格最小边长，通常为高度边，其算式为

lL≥V×T≥lL+1。

(4)

随着网格划分层级增加，其网格数量规模成指数上升，因计算机性能限制，下文直接选定第11，12层级[13]剖分网格进行计算。

假设2(飞行器设定) 假设飞行器的最小转弯半径小于网格边长。在所在层级网格航迹规划时其爬升角、转弯角可以达到，即在该层级及更大层级网格中，当前点周围路径网格都是可行的路径点。

假设3(雷达仿真设定) 假设现有N部雷达，其主要分布在目标点周围，零星几部在整个空域环境中。在置信度为0.9的情况下，以其联合探测概率空间中探测概率大于0.5的网格集合为探测威胁空间。在直角坐标系中其联合探测概率算式[17]为

(5)

式中：σm，Rm分别代表探测概率为0.9的情况下给定目标最大截面积及雷达最远探测距离；θi代表相对于第i部雷达的飞行器反射角；x′i，y′i分别代表第i部雷达的横、纵坐标点。由式(5)可以实现剖分网格规范后的立体空间中雷达联合探测概率威胁空间表征计算。

3.2 剖分网格中改进算法应用可视化

Cesium平台是基于JavaScript编写、由webGL渲染的地图引擎，可用于3D，2D，2.5D形式的地图展示。在该平台框架下结合剖分网格结构，可以展示改进算法结合剖分网格实现立体空间航迹规划的能力。

八叉树结构下的立体空间剖分网格，相较于平面四叉树结构，扩展了高度维，需按各自层级长宽高比定义新的移动路径代价值g(n)和f(n)，但惩罚因子值不变，施加位置在斜飞时变为2个三角锥平面及1个斜平面或直飞时的3个水平面；在变步长设置时，对应的编码位比较在大步长时变为n-3位。选定作战任务想定空域为(118°E～122°E,22°N～25°N)。随机设定4个性能相同的地基雷达[17]，其σm,Rm分别为4 m2和60 km。将飞行器起、终点设置为(118°32′E，24°45′N，0 km)和(121°31′E，23°55′N，10 km)。

最终生成航迹如图8所示。其中，白色线段连接的各节点构成飞行器的可行航迹，改进算法在剖分网格中得到有效应用，具有剖分网格全球可用，层级可调的优点。

图 8 剖分网格组织下航迹示意Fig.8 Trajectory diagram under subdivision grid organization

4 结论

针对飞行器远距离突防时的雷达威胁分布特点，基于栅格环境的剖分网格空间组织理论，提出了一种结合剖分编码空间-信息表征特点的改进A*算法。其生成的航迹与原方法相比，突出了指向性优势和分段变步长航迹规划的思想。该算法可以使计算节点大大减少，计算效率显著提升，同时相较于原算法，能很好地适应威胁区域集中的突防任务航迹规划。最后通过Cesium平台在剖分网格空间组织下结合改进算法进行了实际演示。但本文并未对航迹进行平滑处理，在最终航迹里还存在一些不必要的转折角，这将是下一步拓展的方向。