轨道交通列车永磁同步电机涡流损耗抑制措施研究*

于海阔 张利军 靳 凯 毕京斌 赵海波

(1. 中车青岛四方车辆研究所有限公司， 266031， 青岛；2. 中车长春轨道客车股份有限公司， 130062， 长春∥第一作者， 工程师)

0 引言

轨道交通列车应用的PMSM (永磁同步电机)以其损耗小、效率高、体积小、质量轻、结构多样化、可靠性高、过载能力强等优点成为轮毂电机的首选。但是，在PMSM中，永磁体和带槽电枢铁心相互作用，产生齿槽转矩，进而产生振动和噪声，影响系统的控制精度。除此之外，受轮毂电机体积限制，永磁体产生的涡流损耗会使其自身产生高温，面临不可逆退磁的风险。

从PMSM齿槽转矩产生的机理出发，削弱齿槽转矩大致可从极和槽两方面考虑。文献[1]从磁极优化角度出发，把减小气隙磁密谐波分量作为削弱齿槽转矩的依据，分析了不同转子磁极优化技术的优、缺点。文献[2]采用优化磁极形状的方法，提出了两种凸形不等厚磁极的永磁电机，相比于传统表贴瓦片形永磁电机降低了rTHD(气隙磁密谐波畸变率)和齿槽转矩，增大了电磁转矩，但未分析对电机转矩脉动的影响。文献[3]采用偏心磁极来优化表贴式PMSM气隙磁密波形，推导了偏心磁极电机气隙磁密解析表达式；结合样机试验证明了计算方法的准确性，但是生产制造复杂、成本高。不同于磁极优化技术，研究电机解析模型中定子开槽对气隙磁场的影响，可进一步分析齿槽转矩。文献[4]在文献[5-6]的基础上，采用保角变换法推导出二维极坐标系下的相对磁导函数，进而得到表贴式PMSM定子开槽状况下的气隙磁场分布,但所得到的气隙磁场分布并不完整。文献[11]采用保角变换法推导出复相对磁导函数，得到完整的气隙磁场分布，但求解过程复杂、计算时间长；定子槽为无限深单槽模型，无法考虑槽与槽间的影响，不利于反电势的精确计算。文献[12]采用数值、解析相结合的方法推导了定子开槽下PMSM气隙磁场分布，但计算耗时长，且受迭代精度影响。不同于上述文献中提到的开槽PMSM气隙磁场解析方法，精确子域模型法能够考虑到定子槽间相互影响，且会根据材料属性和电机结构将电机划分为不同的子域，在计算电磁性能方面具有较高的精度。文献[13]在PMSM解析建模中考虑了导磁材料磁导率为具体数值的情况，结合精确子域模型法推导了电机气隙磁密，以及空载工况下的反电动势及输出转矩的表达式，探究了极弧系数和槽开口宽度对输出转矩的影响，但未分析对气隙磁密和齿槽转矩的影响，且所建模型中槽型尺寸仅由槽口宽度决定，实用性较差。

针对永磁体涡流损耗的抑制，最常用的方法是磁极分段。文献[14]研究了Halbach充磁方式下永磁体每极分块数对齿槽转矩的影响，证明每极分块数目越多越能改善磁场分布，但会增加制造成本。文献[15]提出了一种环形部分分段结构，比较了永磁体单侧、双侧部分分段，以及单侧、双侧环形部分分段的涡流损耗。永磁体部分分段在保持一定机械强度的基础上，可以保证永磁体的完整性，不需要额外的工艺及成本。

针对以上问题，以rTHD、齿槽转矩及涡流损耗最小为优化目标，提出一种十字型部分分段Halbach PMSM解析模型，推导出十字型部分分段并考虑定子开槽效应下的气隙磁密解析表达式，计算得到PMSM的齿槽转矩和电磁转矩，通过有限元仿真验证了解析结果的准确性，并且系统地分析了极间间隔角度、边界磁极的充磁角度、主磁极高度和宽度、剖去部分深度和宽度对径向气隙磁密的基波幅值和rTHD的影响。

1 PMSM解析模型的构建

1.1 PMSM解析模型

建立二维极坐标系，采用精确子域模型法分析定子开槽下的气隙磁场分布。为便于分析计算，做出如下假设：① 永磁体材料具有线性退磁特性；② 忽略端部影响；③ 铁磁材料磁导率无穷大。

图1为十字型部分分段Halbach PMSM在空载工况下的气隙磁场和电枢反应磁场解析模型。

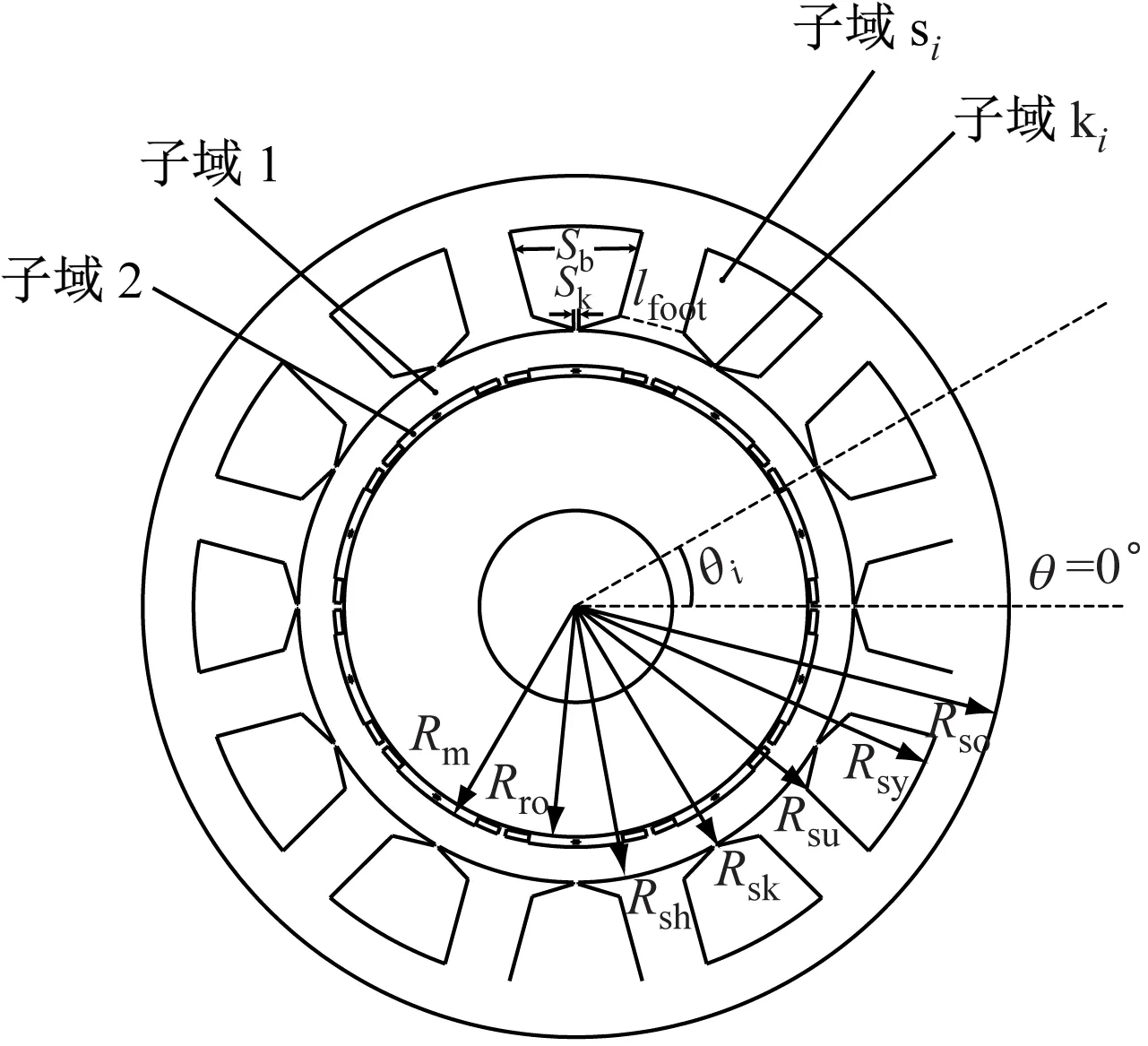
a) 空载工况下的气隙磁场解析模型

b) 电枢反应磁场解析模型

将图1 a) 所示的空载工况下PKPM的气隙磁场解析模型在二维极坐标系下划分为4个区域：气隙区域(1)，永磁体区域(2)，第i个槽口区域(ki)、第i个槽身区域(si)。

将图1 b)所示的电枢反应磁场解析模型在二维极坐标系下划分为3个区域：等效气隙区域(Ι)，第i个槽口区域(Ki)、第i个槽身区域(Si)。

1.2 十字型部分分段Halbach PMSM解析模型

永磁体采用平行充磁。图2为待优化的十字型部分分段磁极结构。在1对磁极下，永磁体磁化强度M可以表示为：

M=Br/μ0

(1)

式中：

Br——永磁体剩磁；

μ0——真空磁导率。

注：lm为主磁极厚度； ls为边界磁极厚度； hm为中心剖去部分厚度。

2 空载工况下PMSM解析模型气隙磁场计算分析

2.1 矢量磁位方程的建立及其求解

空载气隙磁场计算的一般方程为：

(2)

式中：

Mr——径向磁化强度矢量分量；

Mθ——切向磁化强度矢量分量；

A1、A2、Asi、Aki——分别为气隙区域、Halbach型永磁体区域、第i个槽身区域si和第i个槽口区域ki内的矢量磁位；

r、θ——分别为极坐标系下的径向和切向分量。

由分离变量法，得到各区域矢量磁位通解表达式：

(3)

其中:

(4)

式中：

n、m、j——相应区域内矢量磁位的谐波次数；

θ0——转子初始位置角；

g——2p和Q的最大公约数；

A1n、B1n、C1n、D1n、A2n、B2n、C2n、D2n、Asi,j、Asi,m、Aki,0、Aki,j、Bki,j——分别为空载工况下气隙磁场的待定系数；

Mr,n(n)、Mθ,n(n)——分别为Mn(n)的径向和切向磁化强度矢量分量。

各子域边界需满足如下条件：

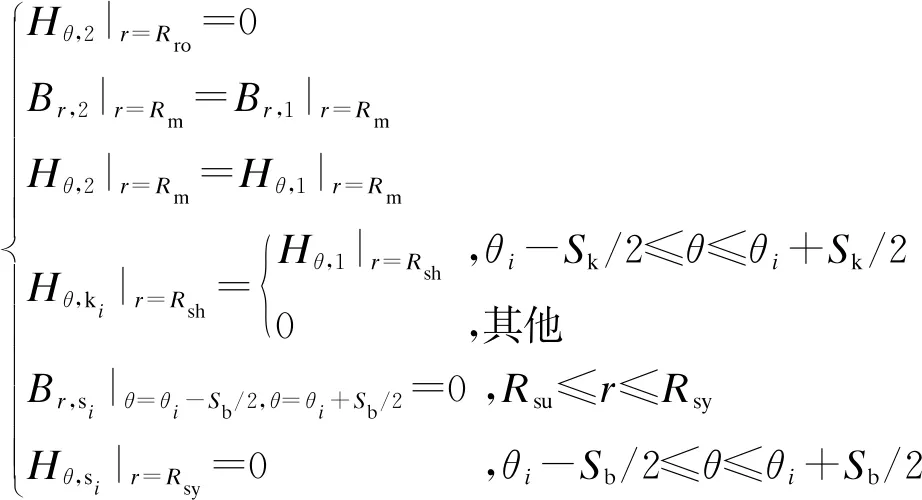
(5)

式中：

Hθ,1、Hθ,2、Hθ,si、Hθ,ki——分别为子域1、2、si、ki的切向磁场强度；

Br,1、Br,2、Br,si——分别为子域1、2、si的径向气隙磁密。

2.2 空载工况下PMSM的气隙磁密

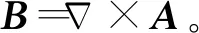
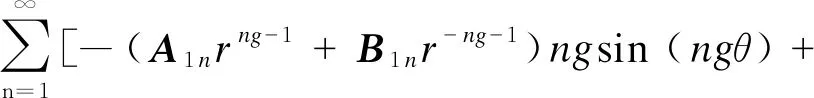
(C1nrng-1+D1nr-ng-1)ngcos (ngθ)]

(6)

(C1nrng-1-D1nr-ng-1)ngsin (ngθ)]

(7)

Bθ,1——空载气隙子域1的切向气隙磁密。

2.3 齿槽转矩的计算

由空载工况下的气隙磁密分布计算结果，利用麦克斯韦应力张量法，得到齿槽转矩Tcog的表达式：

(8)

式中：

Lz——电机轴向长度。

3 PMSM电枢反应磁场解析模型分析

3.1 矢量磁位方程的建立与求解

电枢反应磁场计算时，永磁体不充磁。施加电流源激励后，永磁体磁场计算的一般方程为：

(9)

式中：

AΙ、AKi、ASi——各区域内的矢量磁位；

Ji——第i个槽内绕组的电流密度。

根据前面的分析，笔者认为中国目前政治、社会制度的条件，比如传统的集权影响、幅员辽阔差异巨大、社会自治基础和能力不足等，不具备央地彻底分权模式的条件，可行的模式是应该探索中央统一领导、地方授权执行的分权模式，在其中不断探索合理授权地方的机制，从而实现央地之间权责内洽的机制建立。

由分离变量法，得到各区域矢量磁位通解的表达式：

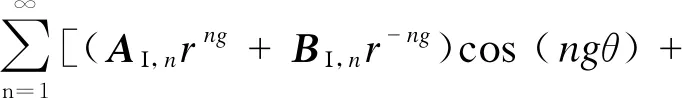
(CΙ,nrng+DΙ,nr-ng)sin (ngθ)]

(10)

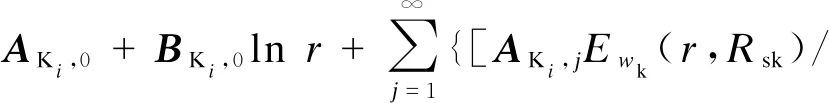
Ewk(Rsh,Rsk)-BKi,jEwk(r,Rsh)/

Ewk(Rsh,Rsk)]cos[wk(θ-θi+Sk/2)]}

(11)

ASi=ASi,0+ACi(r)+

(12)

式中：

AΙ,n、BΙ,n、CΙ,n、DΙ,n——子域Ι电枢反应气隙磁场的待定系数;

AKi,0、BKi,0、AKi,j、BKi,j——子域Ki电枢反应气隙磁场的待定系数;

ASi,0、ACi、ASi,m——子域Si电枢反应气隙磁场的待定系数。

各区域的边界条件如下：

(13)

式中:

Hθ,Ι、Hθ,Ki——分别为子域Ι、Ki的切向磁场强度;

ASi,1、ASi,2——分别为槽身子域Si处绕组1和绕组2产生的磁位。

3.2 等效气隙磁密的计算

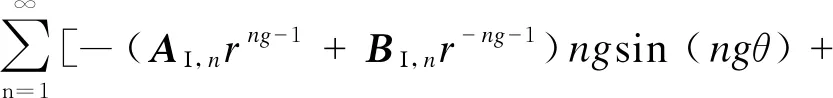
(CΙ,nrng-1+DΙ,nr-ng-1)ngcos (ngθ)]

(14)

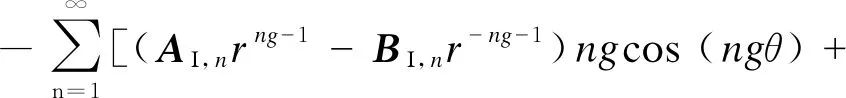
(CΙ,nrng-1-DΙ,nr-ng-1)ngsin (ngθ)]

(15)

式中：

Br,Ι——电枢反应磁场等效气隙子域Ι的径向气隙磁密；

Bθ,Ι——电枢反应磁场等效气隙子域Ι的切向气隙磁密。

4 负载工况下PMSM的磁场分析

4.1 气隙磁密的计算

由叠加定理可得：

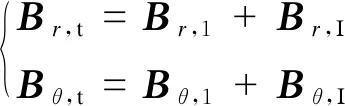
(16)

式中:

Br,t、Bθ,t——分别为负载气隙子域径向和切向气隙磁密。

4.2 电磁转矩的计算

由负载气隙磁密分布结果，利用麦克斯韦应力张量法，得到电磁转矩Tem的表达式：

(17)

式中：

re——电磁转矩积分半径。

5 十字型主磁极中心部分分段Halbach PMSM解析模型有限元分析验证

为验证上述解析模型的正确性，对如图3所示的十字型部分分段Halbach PMSM模型进行有限元仿真分析。该电机模型是在Halbach阵列基础上添加了极间隔断，并将每极分为不等宽、不等厚的3块。为降低涡流损耗，得到更加正弦的气隙磁密波形和较低的齿槽转矩，对主磁极中心部分进行分段，使边界磁极几何中心与主磁极几何中心在同一条圆弧上。电机模型的主要参数如表1所示。根据解析计算结果对永磁体的极间间隔角度、边界磁极的充磁角度、主磁极高度和宽度、剖去部分深度和宽度进行多变量分级优化设计，并与普通表贴结构、普通表贴部分分段结构、等厚等宽Halbach结构、T型Halbach结构、Hat型Halbach结构、T型部分分段Halbach结构及Hat型部分分段Halbach结构的电磁性能进行对比，验证十字型部分分段Halbach PMSM结构的有效性及优越性。

图3 十字型部分分段Halbach PMSM模型示意图

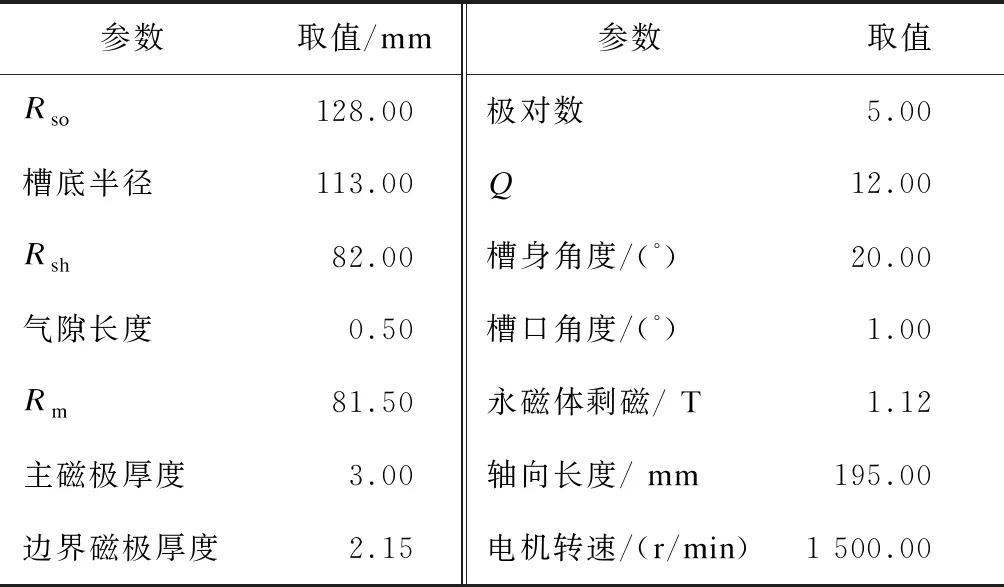
表1 十字型部分分段Halbach PMSM的主要参数

5.1 空载工况下PMSM的仿真波形

图4～5为空载工况下的十字型部分分段Halbach PMSM解析模型和FEA(有限元分析)模型的气隙磁密和齿槽转矩[17]。

图4 不同模型下气隙磁密随机械角度变化对比曲线

图5 不同模型下齿槽转矩随机械角度变化对比曲线

由图4～5可见，PMSM模型的气隙磁密和齿槽转矩的解析解和FEA解基本吻合，验证了PMSM解析模型的正确性，为永磁体结构的进一步优化奠定基础。

对永磁体的极间间隔角度进行优化，以rTHD为确定指标得到极间间隔角度为6°。改变FEA模型中边界磁极的充磁角度b，令b在0°～90°内，每隔10°取1个值，得到空载工况下PMSM模型的气隙磁密基波幅值和rTHD随b的变化曲线，如图6所示。由图6可见，随着b增大，rTHD先略微减小再增大，基波幅值则一直减小；当b=0°时，基波幅值的最大值为1.035 T；当b=10°时，rTHD的最小值为20.8%，基波幅值为1.032 T。因此，选取10°作为边界磁极的充磁角度。

图6 谐波畸变率和基波幅值随b的变化曲线

当极间间隔角度为定值时，主磁极与边界磁极所占角度之和亦为定值。通过改变主磁极角度θm及边界磁极厚度ls，使θm在0°～20°内(每隔2°取1个值)，使ls在1～3 mm内(每隔0.25 mm取1个值)，得到空载工况下PMSM的气隙磁密rTHD的变化曲线，如图7所示。

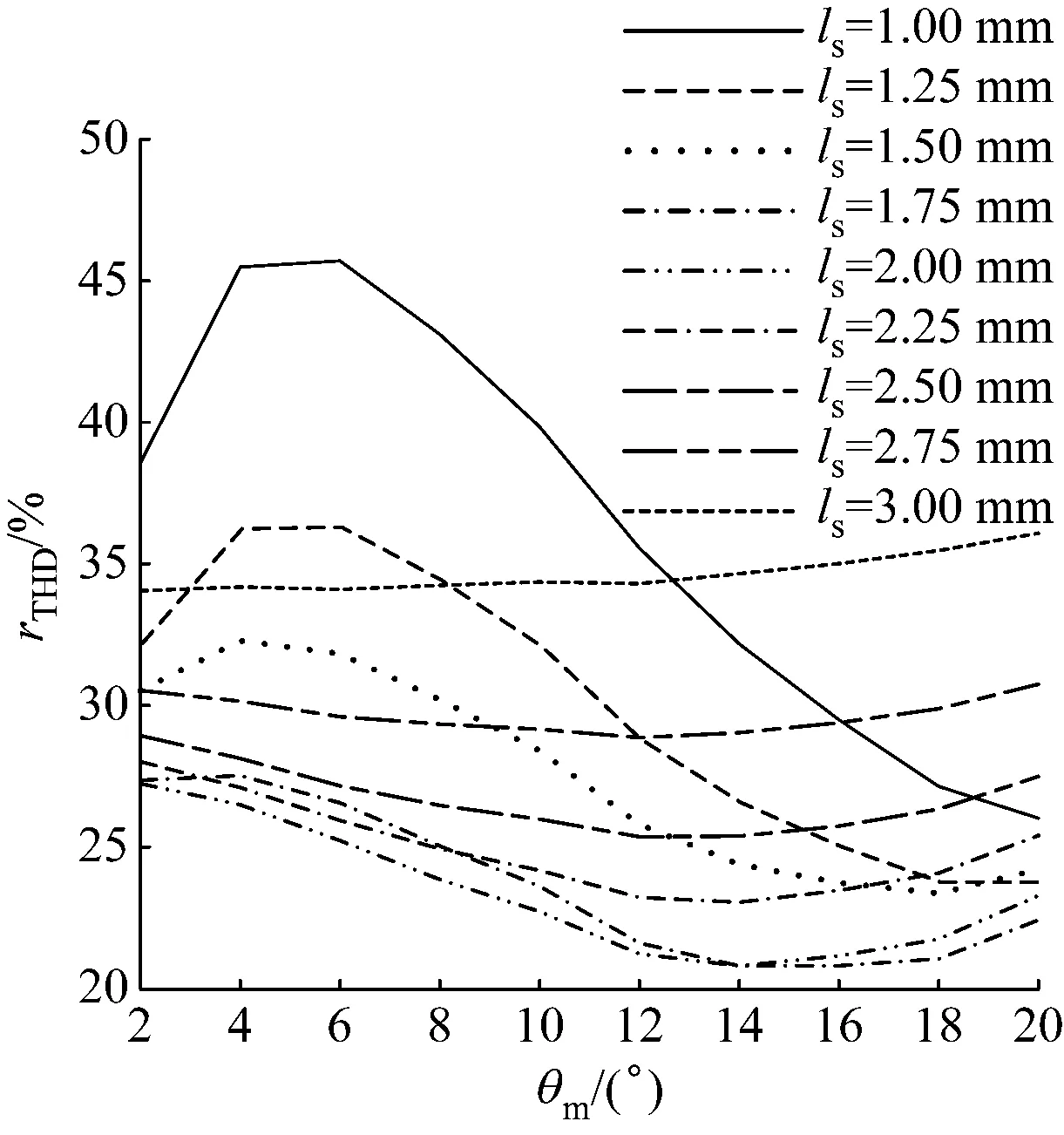
图7 PMSM的rTHD随θm的变化曲线Fig.7 Curve of PMSM rTHDchanging with θm

由图7可见，当θm为定值时，随着ls增大，rTHD先减小后增大，且ls的转折点在1.75～2.00 mm范围内。综合图7仿真结果，令θm在12°～16°内，每隔1°取1个值； 令ls在1.5～1.9 mm内，每隔0.1 mm取1个值，通过进一步优化，得到图8所示曲线。

由图8可见，当ls为定值时，随着θm的增大rTHD先减小后增大，θm的转折点为13°。为进一步缩小最优参数范围，令θm分别为12°、13°、14°时，ls分别为1.7 mm、1.8 mm、1.9 mm。

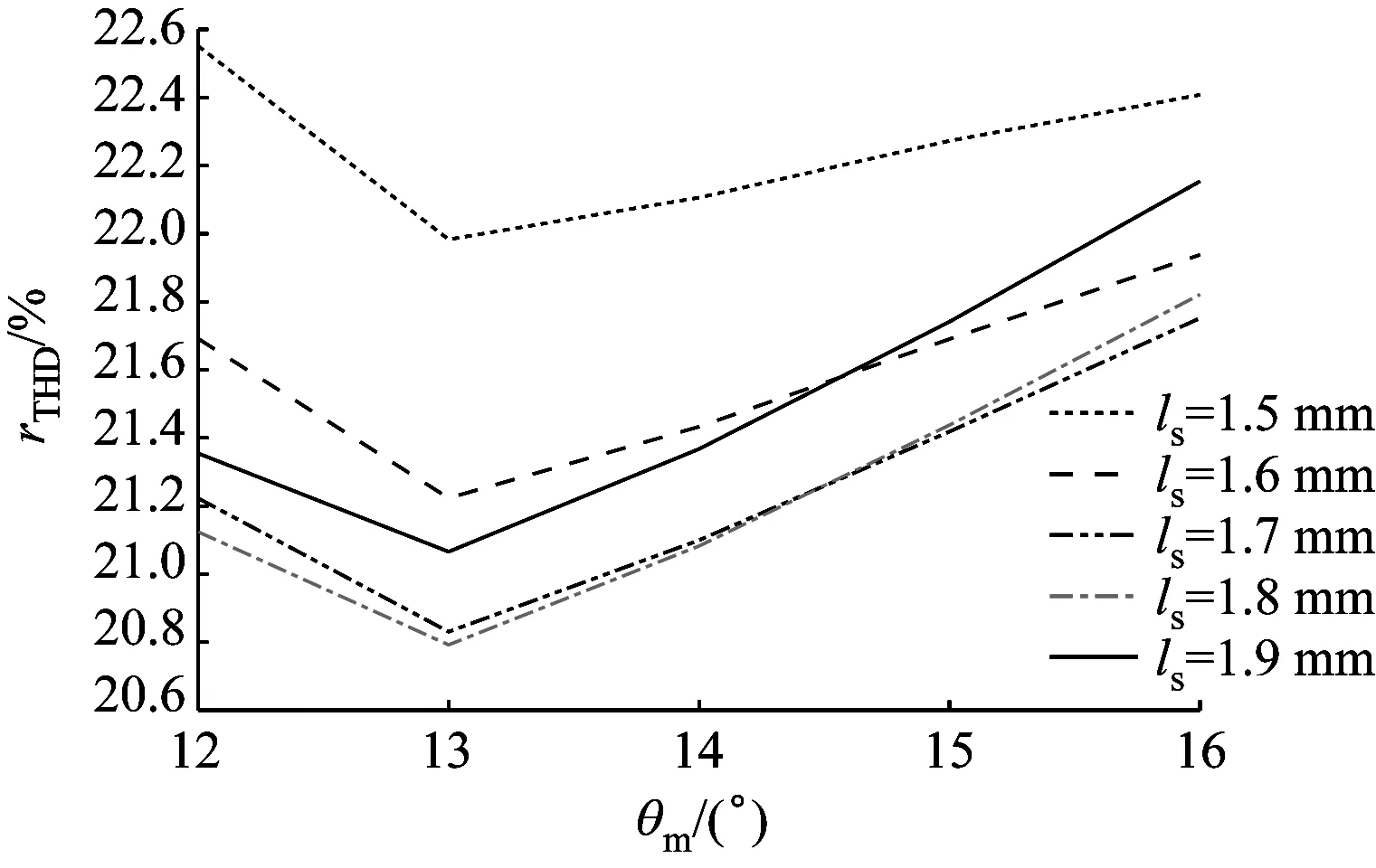
图8 PMSM的rTHD随θm的变化曲线Fig.8 Curve of PMSM rTHDchanging with θm

改变PMSM有限元模型中主磁极中心部分分段深度hm和角度θcm。令hm在0～3 mm内，每隔0.5 mm取1个值；令θcm在0°～30°内，每隔3°取1个值。得到空载工况下rTHD随θm的变化曲线，如图9所示。

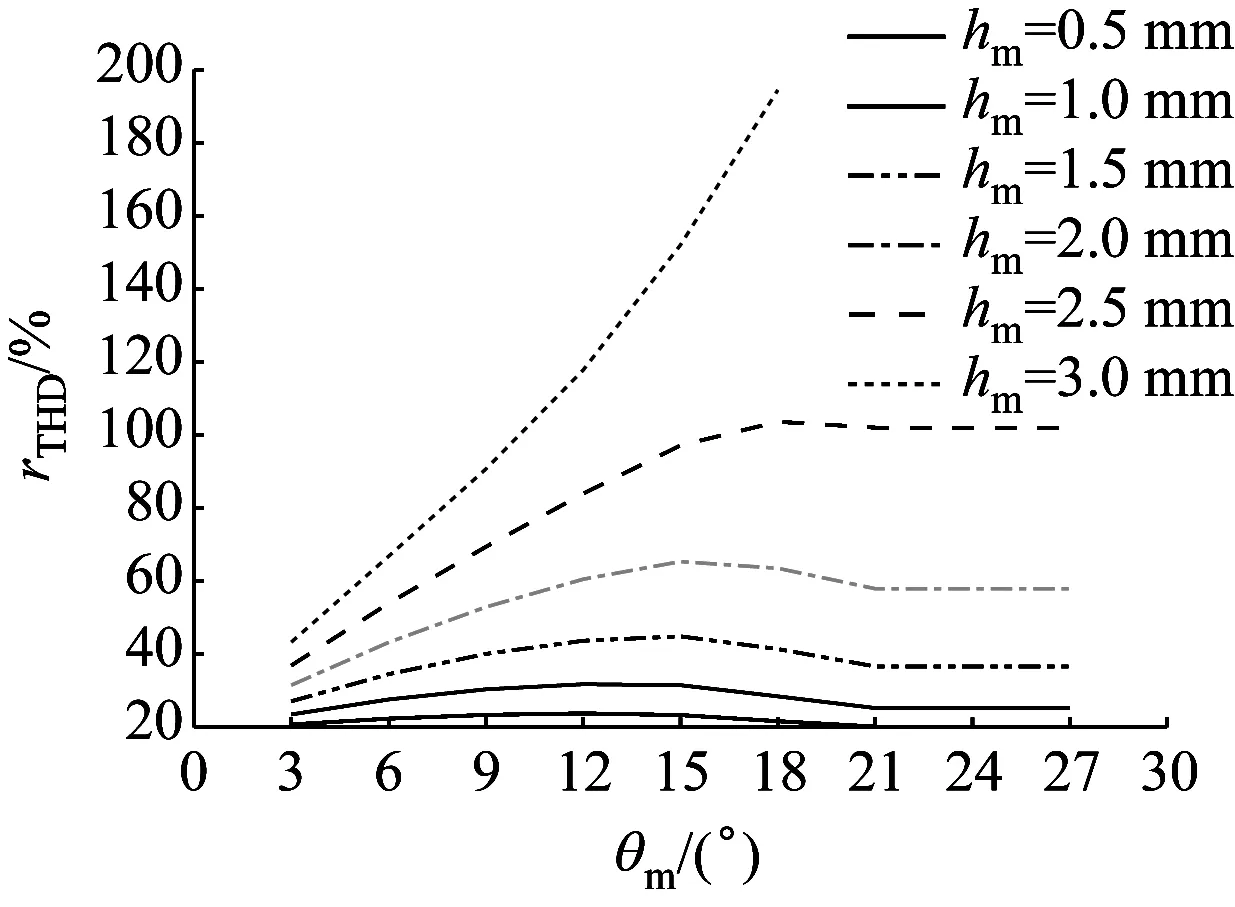
图9 PMSM的rTHD随θcm的变化曲线Fig.9 Curve of PMSM rTHD changing with θcm

从图9中可以看出，当θcm为定值时，rTHD随hm的增大而增大；当hm为定值时，rTHD随θcm的增大先增大后减小。考虑到永磁体的完整性及机械强度，hm不能超过永磁体厚度的65%，即hm≤1.95 mm。综合图9仿真结果，令θcm在3°～7°内，每隔1°取1个值；令hm在0.1～0.5 mm内，每隔0.1 mm取1个值，通过进一步优化，得到图10所示曲线。

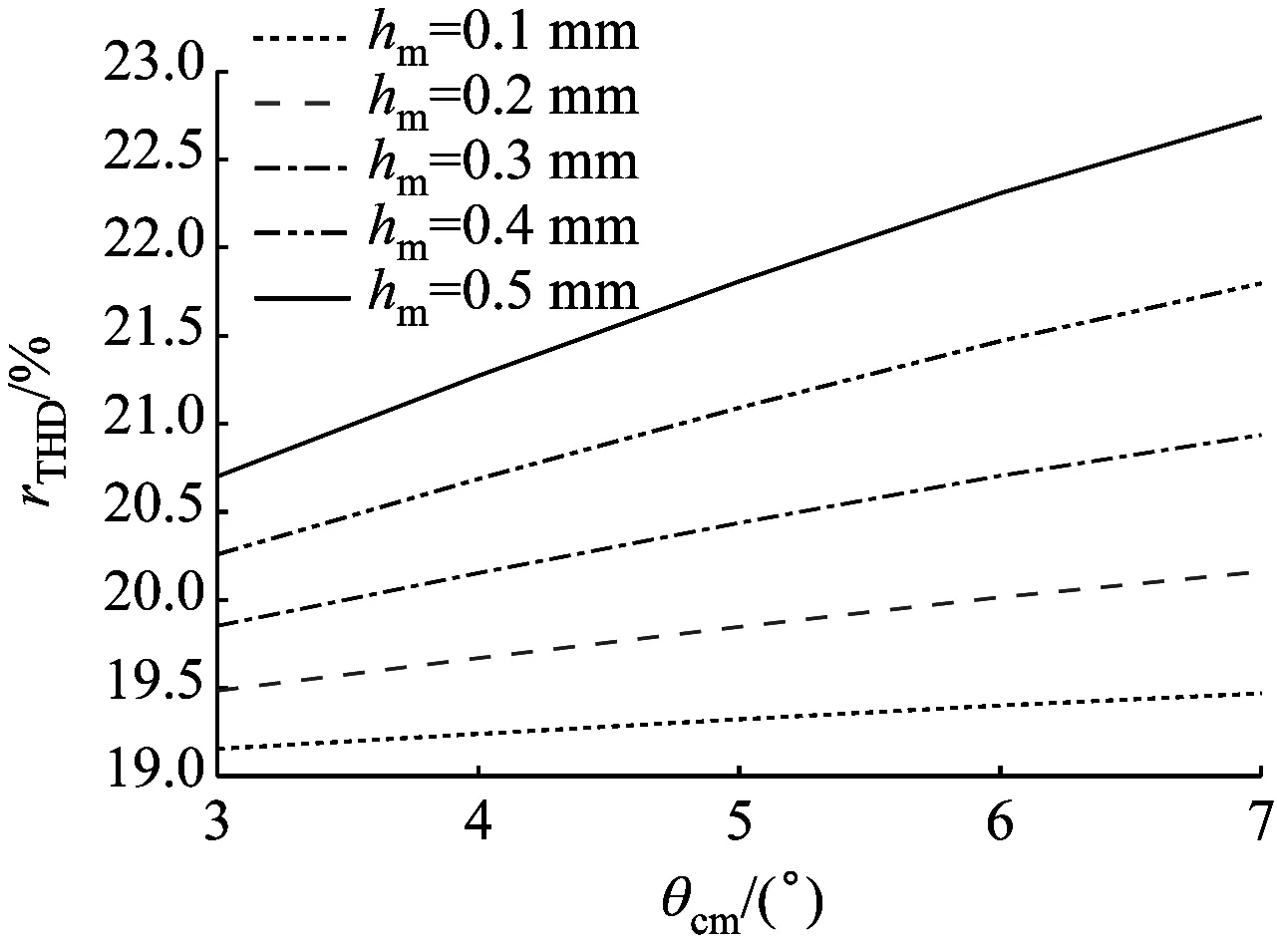
图10 PMSM的rTHD随θcm的变化曲线Fig.10 Curve of PMSM rTHD changing with θcm

综合图10仿真结果，考虑到PMSM实际制作工艺和成本，令θcm分别为3°、4°、5°，hm分别为0.2 mm、0.3 mm、0.4 mm。将θcm、hm与θm、ls进行多变量优化，得到图11所示仿真结果，以寻出最优参数组合。

图11为主磁极剖去角度θcm分别为3°、4°、5°时，rTHD随θm、ls和hm的变化曲线。当θm=13°、ls=1.9 mm、θcm=3°及hm=0.2 mm时rTHD有最优解。至此，在空载工况下完成了对十字型部分分段Halbach结构的优化。将优化后rTHD的最优解应用于其他8种电机结构，得到图12所示的齿槽转矩变化曲线和图13所示的涡流损耗变化曲线。

a) θcm = 3°

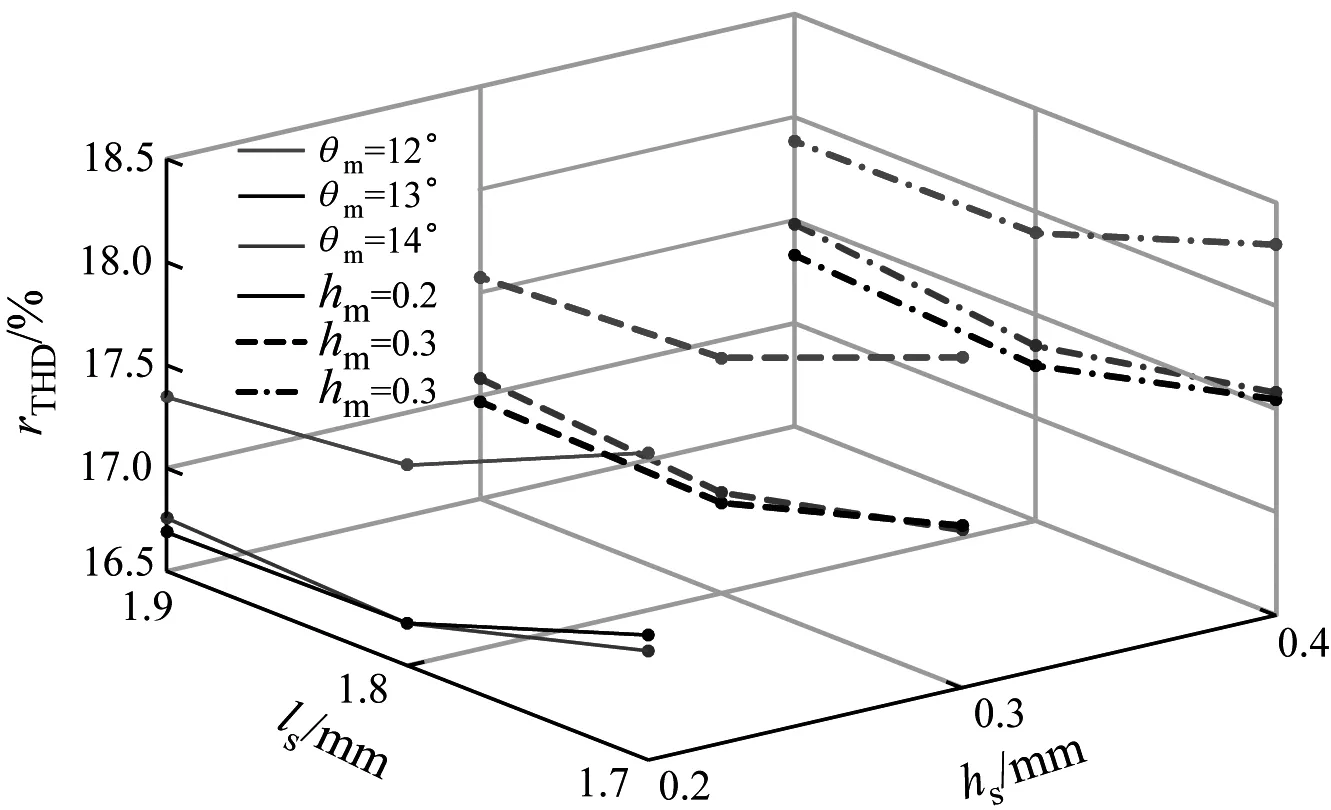
b) θcm = 4°

c) θcm = 5°图11 PMSM多变量优化后rTHD变化曲线

由图12可见，普通表贴式PMSM齿槽转矩为820.27 mNm，普通表贴部分分段PMSM齿槽转矩为832.71 mNm；等宽等厚Halbach PMSM齿槽转矩为585.08 mNm，Hat型Halbach PMSM齿槽转矩为472.02 mNm，Hat型部分分段Halbach PMSM齿槽转矩为459.12 mNm；T型Halbach PMSM齿槽转矩为493.46 mNm，T型部分分段Halbach PMSM齿槽转矩为481.32 mNm；十字型Halbach PMSM齿槽转矩为413.56 mNm，十字型部分分段Halbach PMSM齿槽转矩为385.84 mNm。

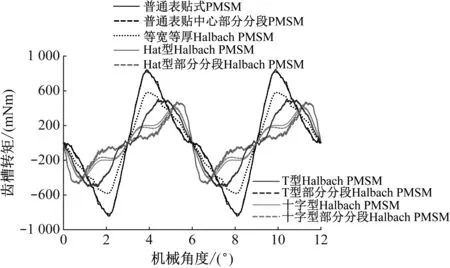
图12 优化后9种电机结构齿槽转矩随机械角度的变化曲线

图13 优化后9种结构涡流损耗随时间的变化曲线

由图13可见，普通表贴式PMSM涡流损耗为61.72 W，普通表贴中心部分分段PMSM涡流损耗为60.29 W；等宽等厚Halbach PMSM涡流损耗为18.68 W， Hat型Halbach PMSM涡流损耗为14.80 W，Hat型部分分段Halbach PMSM涡流损耗为14.23 W；T型Halbach PMSM涡流损耗为14.72 W，T型部分分段Halbach PMSM涡流损耗为14.15 W；十字型Halbach PMSM涡流损耗为14.57 W，十字型部分分段Halbach PMSM涡流损耗为14.03 W。综合上述数据，相比于普通表贴式PMSM，等宽等厚Halbach充磁方式下的PMSM涡流损耗降低了69.73%；相比于Hat型和T型的Halbach PMSM，十字型Halbach PMSM涡流损耗更小；相比于主磁极不分段的PMSM，主磁极中心部分分段结构的PMSM降低了涡流损耗。

5.2 永磁体负载反应磁场仿真波形

空载工况下PMSM的反应磁场和电枢反应磁场的叠加即为负载反应磁场，此时永磁体和激励电流源同时作用。由PMSM的主要参数(见表1)推算出所施加电流源激励的A相电流有效值Im为30 A，A相电流初相位为30°。选取r=(Rsh+Rm)/2作为气隙线半径，提取负载气隙磁密，得到如图14所示波形。由图14可见，负载气隙磁密的解析解与有限元解吻合。电磁转矩的解析解与有限元解对比如图15所示。

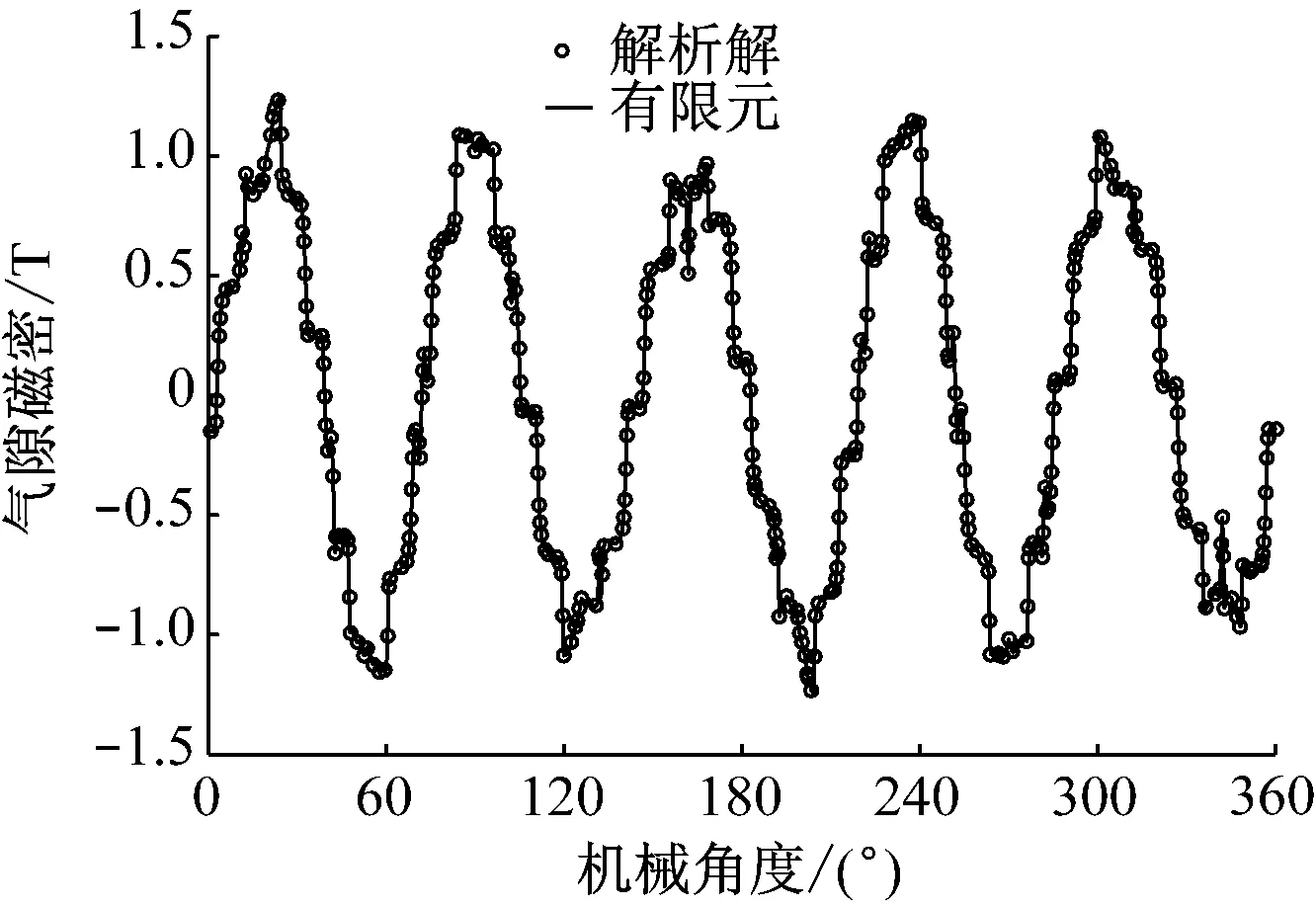
图14 不同模型下PMSM的气隙磁密随机械角度变化曲线

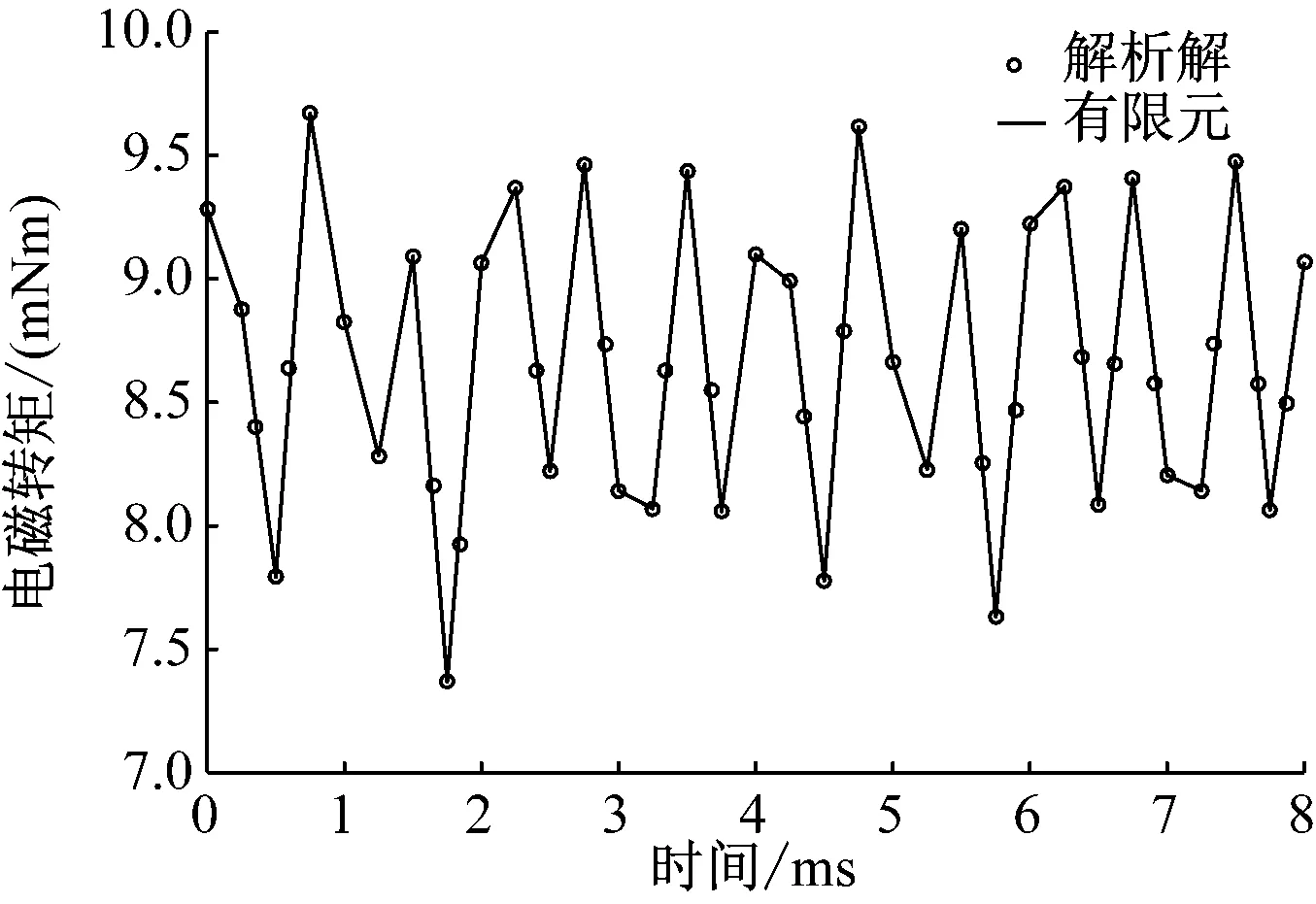
图15 不同模型下PMSM的电磁转矩随时间变化曲线

图15所示为负载工况下PMSM的电磁转矩解析解与有限元解的对比图。图15可见，PMSM的电磁转矩波动较大。图16为优化后的十字型中心部分分段Halbach PMSM和普通表贴式PMSM在负载工况下的气隙磁密变化曲线。由图16可见，十字型中心部分分段结构的PMSM的气隙磁密波形更加正弦。

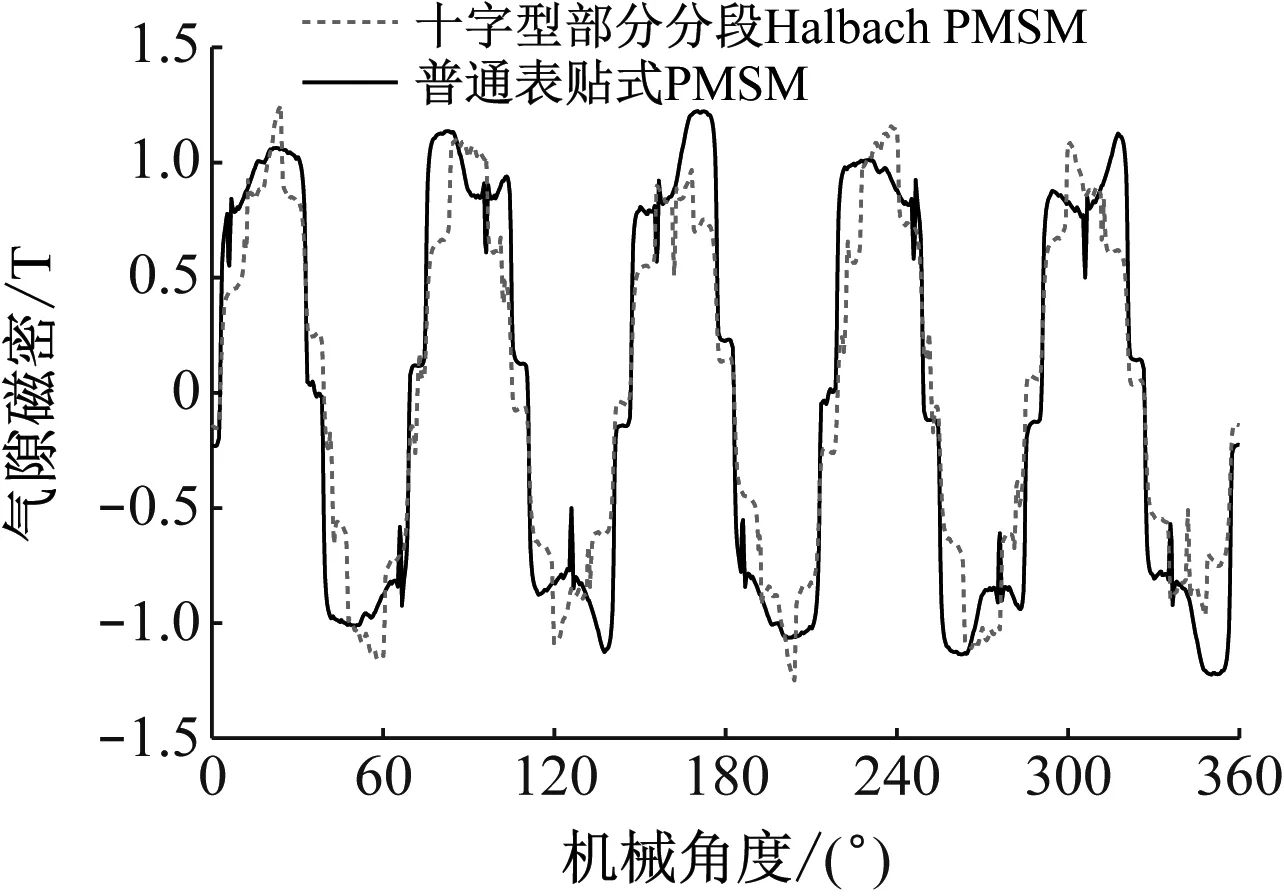
图16 负载工况下PMSM的气隙磁密随机械角度变化曲线

5.3 PMSM机械强度分析

当PMSM转速为1 500 r/min时，在切向离心力和电磁力的作用下，通过仿真得到PMSM的等效应力和总变形，如图17、图18所示。

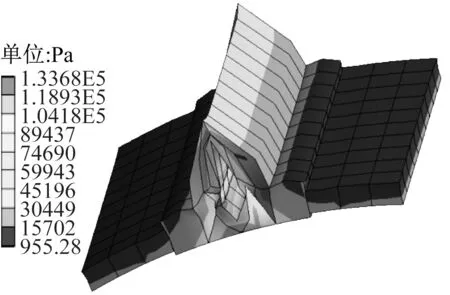
图17 PMSM的等效应力图Fig.17 Equivalent stress map of PMSM

图18 PMSM的总变形图Fig.18 Total deformation map of PMSM

如图17所示PMSM的等效应力，显示了由其切向离心力和电磁力引起的等效应力。由图17可见，永磁体的最大等效应力发生在靠近转子侧，其最大等效应力为1.34×108Pa，低于永磁体拉伸应力80 MPa。因此，永磁体离心力和电磁力引起的等效应力不会破坏永磁体的机械结构。如图18所示PMSM的总变形，显示了永磁体在切向离心力和电磁力作用下导致的结构变形。由18可见，永磁体的最大变形发生在其中心切口边缘，而发生在永磁体底面结构变形很小。

6 结论

1) 在永磁体用量相同的情况下，十字型结构与T型和Hat型结构相比，对涡流损耗的抑制效果相差不大，但在降低齿槽转矩、气隙磁密谐波畸变率方面效果明显。

2) 对于T型、Hat型及十字型结构，对其主磁极进行中心部分分段增大了气隙磁密谐波畸变率。与采用主磁极单侧部分分段结构相比，主磁极中心部分分段结构的气隙磁密谐波畸变率更小。

3) 十字型部分分段Halbach PMPA结构，相比于T型和Hat型部分分段结构，其几何中心与重心重合，机械强度更优。