局部振动压实荷载对地铁车站结构开裂影响分析*

魏度强 余 超 张慧鹏 夏 明 石钰锋

(1.中国铁路南昌局集团有限公司， 330009, 南昌； 2.佛山市铁路投资建设集团有限公司， 528041, 佛山；3.南昌轨道交通集团有限公司， 330038, 南昌； 4.华东交通大学土木工程国家实验教学示范中心， 330013,南昌∥第一作者， 助理工程师)

我国地铁建设快速发展的同时，其质量也越来越受到重视。地铁结构质量好坏直接关系到其自身的运营安全、使用寿命乃至周边环境[1],因此，严格控制车站主体结构变形、开裂等现象变得愈来愈重要。

目前，文献[2-6]分析了不同施工阶段、温度及收缩效应等因素对地铁车站结构裂缝的影响，而针对局部盖挖法施工中，由于回填施工顺序不同造成局部振动压实作用下产生的不均匀沉降而导致其开裂的现象鲜有讨论。

本文将在前期静力分析[7-8]的基础上，通过动力分析，研究在不同振动频率、名义振幅及振动次数下局部振动压实荷载对车站结构开裂的影响程度及其规律。

1 某地铁车站结构裂缝分布特征

1.1 工程概况

某地铁车站(见图1)总长206.1 m，标准段宽21.7 m，车站顶板覆土厚3.0～3.5 m。车站主体结构采用明挖顺作法(局部盖挖法)施工，共分3期：

1) 第1期：施工便桥区车站围护结构及便桥(便桥搭建于围护结构及其下方的混凝土横撑上)，以恢复路面交通。

2) 第2期：施工车站其余区域的围护结构，然后进行基坑开挖及主体施做、顶板回填(回填分区为先便桥两侧，后便桥区)。

3) 第3期：施工车站附属结构。

图1 某地铁车站平面位置图Fig.1 Location plan of certain metro station

便桥与车站主体结构的位置关系见图2。车站结构标准断面见图3。

车站回填采用残积砂质黏性土，分层回填(每层厚0.5 m)并碾压。其中，车站1～12轴范围内共回填7层，18～24轴范围内共回填6层。

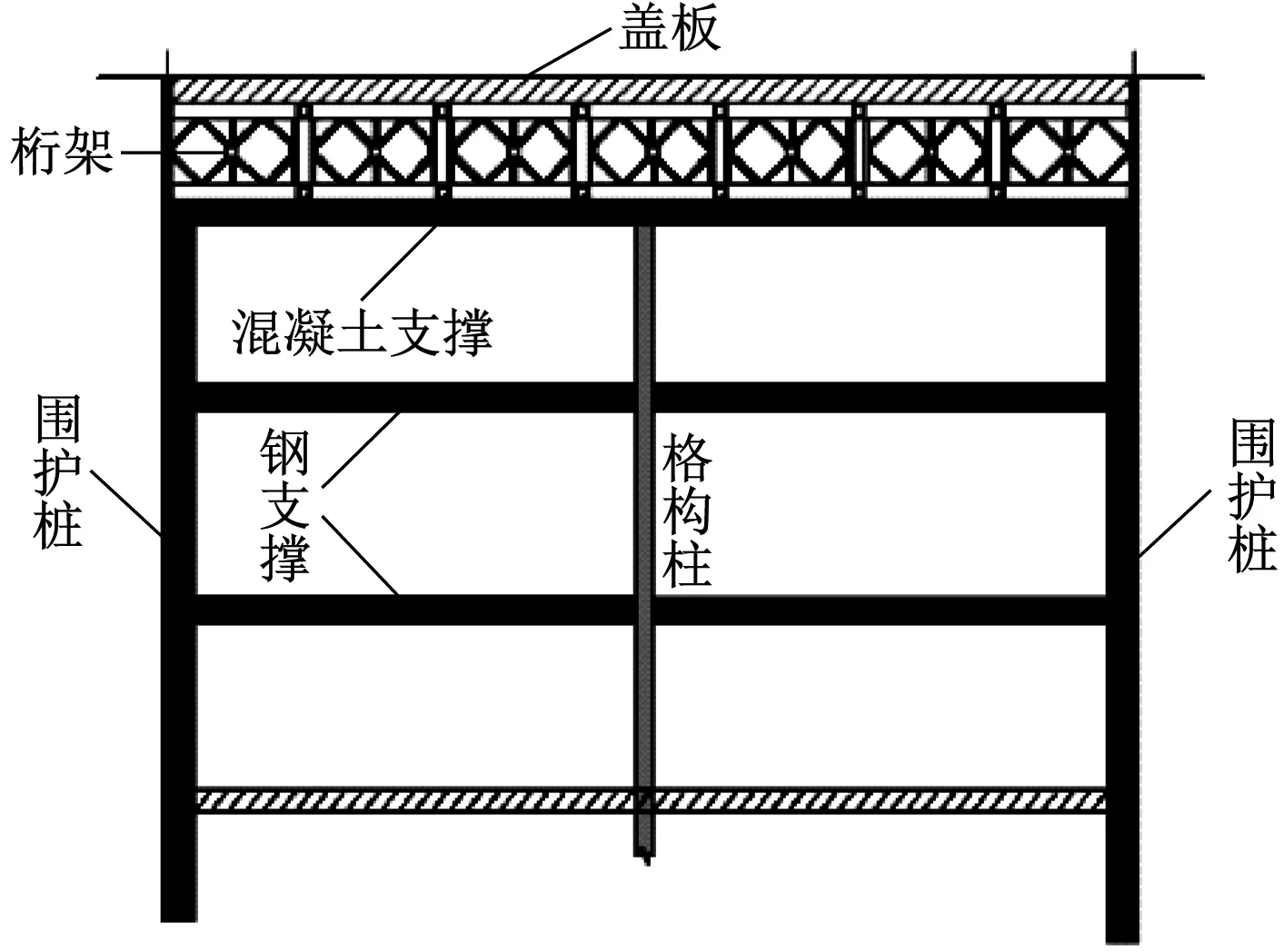
a) 横剖面

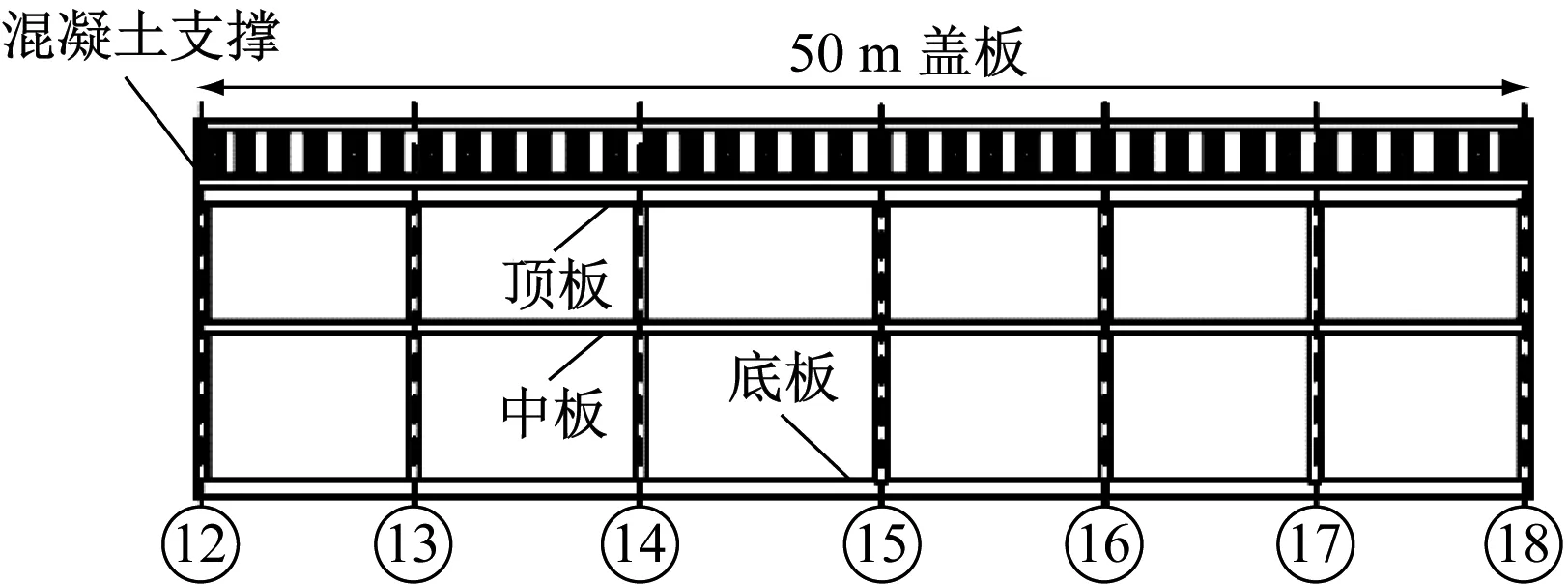
b) 纵剖面图2 地铁车站结构与便桥的位置关系图Fig.2 Location relation of metro station structure and temporary bridge

车站范围内的土层依次为素填土、粉质黏土、残积砂质黏性土、全风化花岗岩、散体状强风化花岗岩(见图3)。车站底板主要坐落于全风化花岗岩上，该土层具有软化性与崩解性，扰动后强度损失大，遇水后易崩解。

1.2 车站结构裂缝分布特征

盖板下方顶板混凝土浇筑完成后4个月，便桥两侧进行土体回填。回填后，便桥下方车站顶板及侧墙区域混凝土结构产生裂缝。车站结构裂缝平面展布图如图4所示。

图3 地铁车站结构标准断面图Fig.3 Standard section of metro station structure

图4 地铁车站结构裂缝平面展布示意图Fig.4 Schematic diagram of plane distribution of metro station structure cracking

由图4可知，车站顶板裂缝主要发生在11～12轴顶板与纵梁之间及13～18轴整块顶板区域，各裂缝间距约2 m，宽度为0.02～0.10 mm，为上下贯穿型裂缝。

通过对实际工程进行分析，发现中板、站台层侧墙和顶板、站厅层侧墙均采取侧墙与板整体浇注的施工方法进行浇筑，浇筑后经检验各板、墙混凝土性质较稳定且差异性小；站厅层顶板及侧墙各部分混凝土强度质量均合格，且裂缝仅在11～18轴范围内发生，其余轴线范围内均无裂缝产生。根据文献[7-8]，该地铁车站结构开裂是由不均匀回填荷载、坑底全风化花岗岩扰动后未处理及压路机振动等综合因素引起的。

2 地铁车站有限元模型的建立

2.1 模型的建立与边界条件的设置

本文通过ABAQUS有限元软件建立车站-土体二维模型(见图5)，模型长500 m、高100 m，对此车站结构进行动力分析。

图5 地铁车站-土体二维有限元模型图Fig.5 Two dimensional finite element model of metro station-soil

考虑到初始静应力条件，地铁车站-土体二维有限元模型计算从静力分析步过渡到动力分析步时，须对模型地基的侧向边界条件进行转换。

土体-地下结构静、动力耦合边界的处理技术主要有两种：一种是文献[9]提出的静-动力统一人工边界技术；另一种是静-动力耦合边界处理技术。静-动力耦合边界处理技术是在静力分析步中，在其侧向边界采用水平向约束和竖向自由的滚轴边界；在动力分析步中，在其侧向边界采用水平向自由和竖向约束的滚轴边界；在静力分析步向动力分析步转化的过程中，将静力分析结束后侧向边界的水平向支座反力采用人工方式以集中力施加于侧向边界上的静力水平支座对应的单元结点上，以此来实现静力边界条件向动力边界条件的转化，具体转化过程见图6。

图6 分析步中静、动力边界条件转换

由于第2种方法概念明确且实施容易，因此，本文中对静、动力耦合作用下车站主体结构侧向边界的处理采用第2种方法。

2.2 车站-土体模型本构关系与参数的选择

采用摩尔-库仑本构模型及NewMark-β法研究局部振动压实荷载作用对地铁车站的影响规律。土体采用Rayleigh阻尼，地下连续墙、车站梁-柱及楼板结构采用线弹性本构。根据模态求得的固有频率对该模型进行有限元计算。地铁车站-土体二维有限元模型所选参数见表1～2。

表1 某地铁车站土层物理力学参数表

表2 某地铁车站结构设计参数

2.3 振动压路机荷载

振动压路机的振动参数主要由其参振质量md、振动频率f与名义振幅A0决定[10]。由于振动压路机的工作振幅是一个随机参数，为便于评价和比较不同机型振动压路机的振动性能，引入了“名义振幅”概念。表3为实际工程中所用的振动压路机参数。当已知振动压路机的参振质量md、振动频率f与名义振幅A0时，压路机激振力F0的计算公式为：

F0=mdA0(2πf)2

(1)

表3 振动压路机参数表

2.4 模拟工序

1) 对车站结构及周围土体进行初始地应力计算；

2) 施加静荷载模拟不同区域土体的回填；

3) 对基坑不同区域分步施加如图7所示的动力荷载,模拟振动压路机振动压实过程。

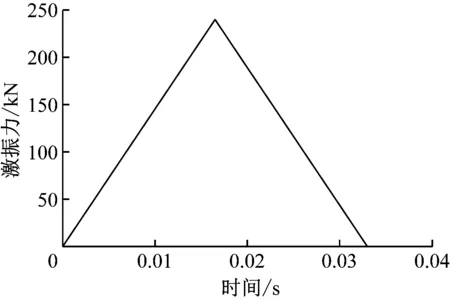
图7 压路机荷载模型Fig.7 Load model of road roller

3 地铁车站模拟数据与监测数据对比

车站施工过程中的监测内容主要包括：①围护桩顶水平位移监测；②围护桩顶竖向位移监测；③围护桩水平位移监测；④地表沉降监测；⑤基坑底部沉降监测。车站基坑监测点平面布置图见图8。

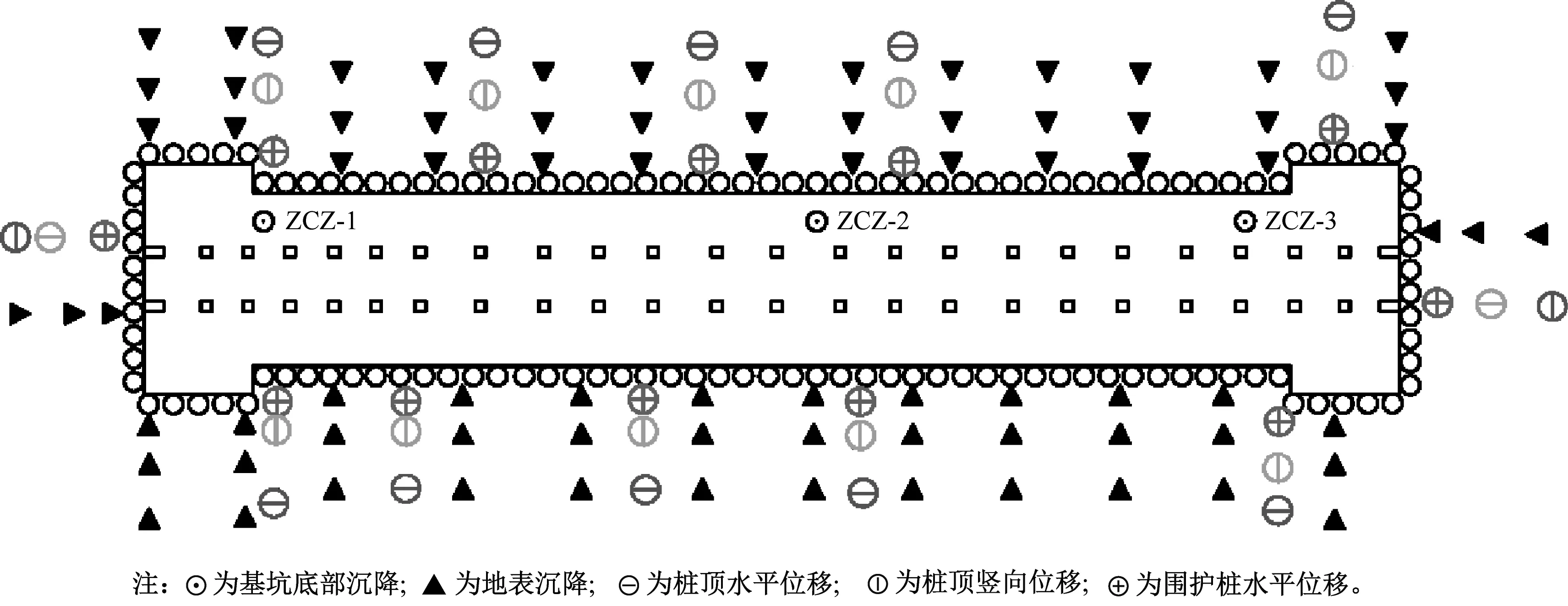
图8 地铁车站基坑监测点平面布置图

由于本次模拟未考虑基坑开挖过程，仅考虑土体回填过程对地铁车站的影响，故监测数据仅选取了基坑底部ZCZ-1、ZCZ-2、ZCZ-3 3点。选取2016年11月基坑开挖完成至2018年1月盖挖区两侧土体回填完成期间基坑底部标高变化量进行对比分析。

图9为车站基坑现场监测数据、静力分析与动力分析结果对比曲线。由图9可知，使用振动压路机对盖板两侧土体回填并压实的过程中，地铁车站主体结构会发生较大的不均匀沉降。不论是静力分析[10-11]还是动力分析，车站基坑底部的整体沉降均与实际监测数据吻合，采用静力分析法得到的数据可能会偏大，动力分析法得出的数据与实测数据较为接近。这表明本文所采用的动力分析法数值模拟是可行的,且较之静力分析更为合理。

图9 地铁车站基坑底部模拟数据与监测数据对比

4 不同振动压实荷载对地铁车站结构的影响

4.1 振动压路机振动次数对地铁车站的影响

为研究振动压路机振动次数对地铁车站结构开裂的影响，选取表4所示的4种工况，对车站顶板上表面应力分布及基坑底部最大沉降差进行分析。

表4 不同振动次数工况表

如图10所示，振动压路机振动次数所引起的地铁车站上表面应力分布情况是一致的，但是随着振动次数的增加，车站顶板上表面最大应力会呈现先增加后减小的趋势。

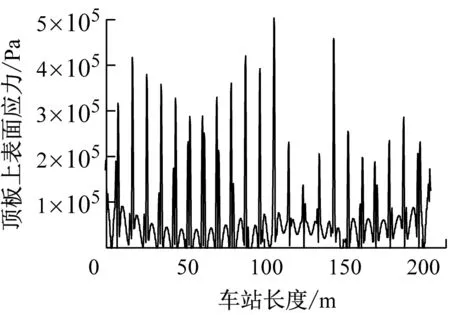
a) 工况1

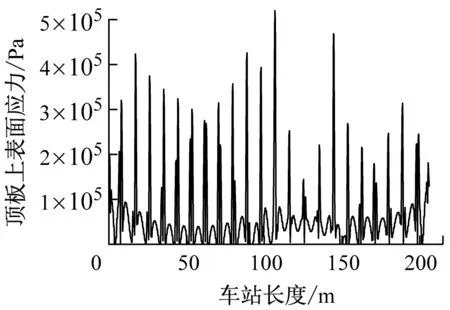
b) 工况2

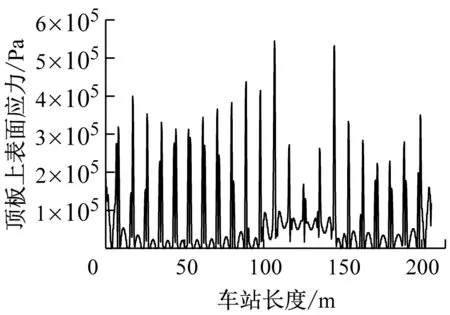
c) 工况3

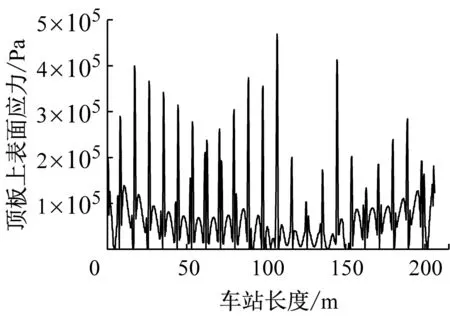
d) 工况4

由表5所示，振动压路机振动30次时，基坑底部土体最大沉降差值达到最大，而振动60次时土体的沉降差反而降低到比振动5次时的数值还小。这可能是由于土体较为松散时，随着振动次数的增加，土体以塑性变形为主，且其变形量较大；而随着土体密实度的提高，土体塑性变形量减小，且振动次数的增加对土体变形量影响较小。

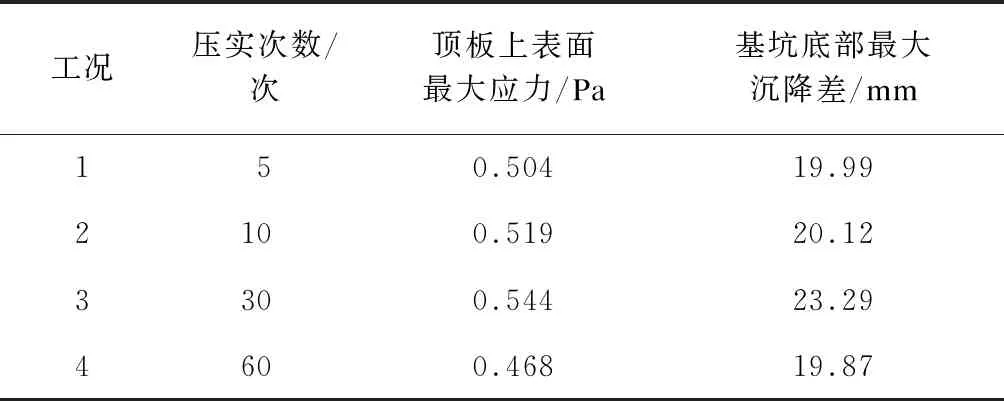
表5 不同压实次数下车站顶板上表面最大应力和基坑底部最大沉降差

4.2 振动压路机名义振幅对地铁车站的影响

如表6所示，选取1.2 mm、1.5 mm、1.8 mm等3种不同名义振幅，分别在振动频率为30 Hz，振动次数为5、10、30、60次的条件下，研究名义振幅对地铁车站的影响。

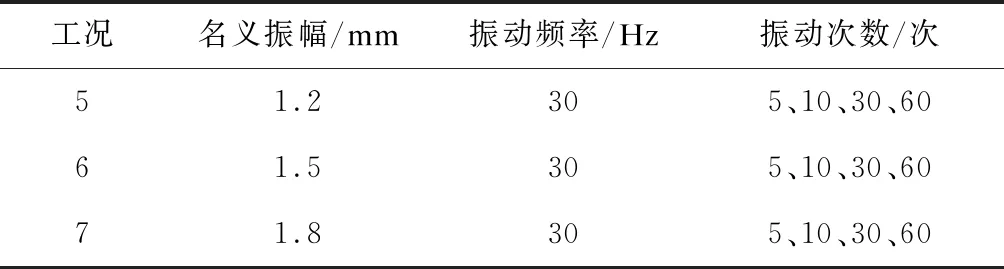
表6 不同名义振幅工况表

由图11 a)可知，车站顶板上表面最大应力值随着名义振幅的增大而逐渐增加；当名义幅值为1.2 mm时，振动压路机振动5次造成的最大应力值约为0.519 MPa；当名义幅值为1.5 mm时，顶板上表面最大应力值约为0.545 MPa，仅比名义幅值为1.2 mm时增加了约4.7%；而名义幅值为1.8 mm时，车站顶板最大应力值达到了0.656 MPa，较名义振幅为1.2 mm时增幅高达26.3%。

由图11 b)可知，除振动30次外，在名义振幅为1.2 mm时，振动5、10、60次时的基坑底部土体最大沉降差较为接近，均接近20 mm。但随着名义振幅的增加，不同振动次数下基坑底部的最大沉降差变化规律相差较大。振动次数为30次时，随着名义振幅的增加，基坑底部的最大沉降差呈现出较大的增长，从名义振幅为1.2 mm时的23.28 mm增加到名义振幅为1.8 mm时的41.48 mm，增幅接近1倍；而当振动次数为60次时，随着名义振幅的增加，基坑底部最大沉降差值变化不大，仅由名义振幅为1.2 mm时的19.87 mm增加到名义振幅为1.8 mm时的21.05 mm。

a) 顶板上表面最大应力

b) 基坑底部最大沉降差

4.3 振动压路机振动频率对地铁车站的影响

如表7所示，选取2 Hz、5 Hz、10 Hz、20 Hz、30 Hz等5种不同振动频率，分别在名义振幅为1.2 mm，振动次数为5、10、30、60次的条件下，研究不同振动频率对地铁车站的影响。

表7 不同振动频率工况表

由图12可知，随着振动频率的增加，地铁车站顶板上表面最大应力值与基坑底部最大沉降差值均呈现先增加后减小的趋势；当振动频率为10 Hz时，车站顶板上表面最大应力约是振动频率为2 Hz时的1.25倍，而基坑底部土体最大沉降差值约是振动频率为2 Hz时的1.5倍。

a) 顶板上表面最大应力

b) 基坑底部最大沉降差

由此可见，该基坑底部土体存在一个合适的共振频率范围，在此共振频率范围内，土体会得到充分压实使得沉降差扩大，从而导致车站顶板上表面拉应力增加产生开裂；而当基坑底部土体超过该频率后，由于土体过于密实其相对沉降差会减小，车站顶板上表面拉应力亦会随之减弱。

5 结论

1) 静力模拟和动力模拟整体趋势类似并与监测数据吻合，但静力模拟数据明显偏大，而动力分析更为准确。

2) 对振动压路机振动压实荷载影响较大的主要是其名义振幅与振动频率，振动次数对基坑底部沉降差的影响较小。

3) 当土体比较松散时，在振动压路机振动碾压下，基坑底部土体的变形量较大，且其随着压实次数的增加而逐渐增大；而随着土体密实度的提高，土体在振动压实下变得更为密实，基坑底部沉降量会随着压实次数的增加而降低。

4) 振动次数与振动频率的增加均会使得基坑底部最大沉降差呈现先增大后减小的趋势，而最大沉降差会随着名义振幅的增加而增大。

5) 当振动压路机振动频率为10 Hz、名义振幅为1.8 mm时，土体最大沉降差值最大，使局部盖挖后填区车站主体结构产生应力集中，承受较大拉应力，可能使得顶板发生开裂。