基于竞争神经网络的逆变器状态识别方法研究

张 浩，李小波，张冬冬，张 程，汪 翔，吴竑霖

（上海工程技术大学 城市轨道交通学院，上海 201620）

0 引 言

辅助逆变器是地铁车辆的重要组成部分，为车内的空调、风机、照明等辅助设备提供电能。在辅助逆变系统工作过程中除去结构性故障，滤波电容的软故障较为突出。电容软故障是指因自然老化或大电流充放电冲击，导致电容存储电荷能力衰退。目前针对软故障诊断，主要包含特征提取与故障分类两方面，特征提取是找出研究样本中对软故障较为敏感的参数，故障分类是通过提取出的参数进行电路状态识别。在辅助逆变电路故障诊断中，针对选取的测点信号常在频域、时域以及时频域上进行故障特征参数提取，现有的辅助逆变电路诊断研究多集中于硬故障，故障特征参数有小波分解低频系数、EEMD分解出的IMF分量、分形维数等。软故障的研究相对较少，所选取的故障特征参数有小波包分解系数、VMD分解出的模态分量等。这些时频域信号处理方法所提取故障特征参数对硬故障的诊断有较高的准确率，但是并不能充分反映软故障电路状态平稳信号的特点。

本文针对辅助逆变电路的状态识别提出了基于时域特征提取的办法，建立电路全体模式的模糊相似矩阵并采用竞争神经网络模型分类的方法识别软故障，计算量小、过程简单，无需复杂的变换与分解。

1 电路分析

1.1 辅助逆变电路仿真

辅助逆变供电系统的核心部分由输入电路、逆变电路、滤波电路以及输出电路组成。以上海地铁明珠线为研究对象在MATLAB中搭建地铁车辆辅助逆变器仿真模型，地铁车辆辅助逆变电路原理如图1所示，按照明珠线逆变器实际参数设置，其中直流电压源为650 V，IGBT逆变桥的载波频率为6 kHz，载波比为12，滤波电路部分滤波电感值为0.25 mH，阻值为2 mΩ；滤波电容部分为3个78μF的电容以及一个0.5μF的接地电容。为了接近实际电路，负载采用0.62Ω的电阻与1 mH的电感串联而成的阻感负载。

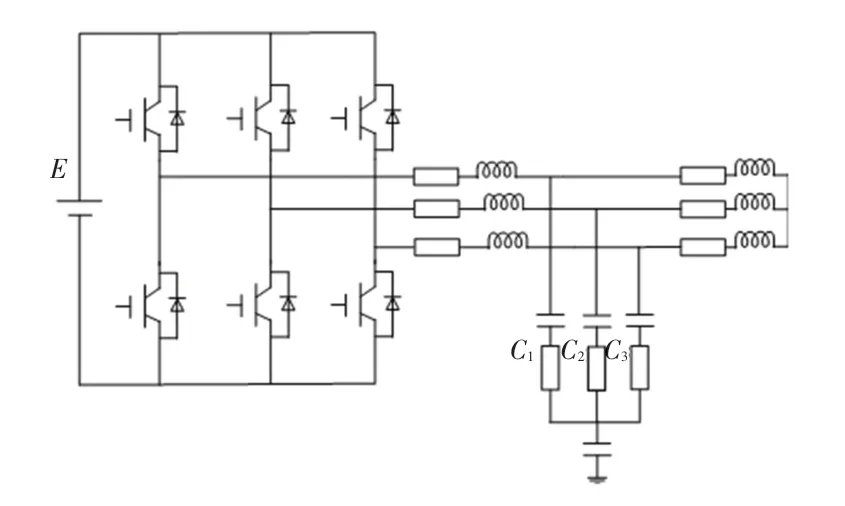
图1 辅助逆变电路原理图Fig.1 Schematic diagram of auxiliary inverter circuit

1.2 电路状态分析

电子电路故障可分为参数性故障和结构性故障。参数性故障称为软故障，表现为元器件参数值偏离标称值的容差范围，并不影响电路的正常工作且无明显征兆，但会使系统性能发生偏离，存在安全隐患。随着车辆运行，元件参数值偏离程度增大，软故障就会转化成硬故障，最终导致电路部分功能丧失，严重时可引起车辆的运行故障。在实际电路中电容并非理想元器件，存在等效电阻。随着电容的使用时间增加，电容的电解液逐渐蒸发，引起电容值衰减以及等效串联电阻阻值增大，造成电容失效，电力电子电路中电容的失效率高达60%。通常以电容值减少20%或超过初始值的2倍作为电容的失效判据，一般认为电容容差在10%以内属于正常范围，因此本文根据电容值衰减以及值增大，故障模式见表1。

表1 故障模式表Tab.1 Failure mode table

分别改变电容容量以及数值大小进行电路仿真，电容正常情况、单个电容软故障情况、单个电容值超出软故障临界值情况3种状态下的逆变器输出电压波形，如图2所示。可看出正常情况输出波形为对称的三相交流正弦波，软故障波形与正常情况相比有轻微波动，超出软故障临界值的波形已产生明显的畸变，电路功能受到影响。

图2 辅助逆变器输出电压波形图Fig.2 Auxiliary inverter output voltage waveform

2 时域特征参数

在信号的时域特征提取过程中，时域信号的相关指标通常可分为有量纲参数与无量纲参数。通常地铁车辆辅助逆变电路的软故障信号十分微弱，难以识别，不同软故障信号之间边界模糊。为了避免不同时域特征单位尺度的差异性对后续数组相似度计算带来影响，本文选用偏度因子、脉冲因子、裕度因子、峭度因子、波形因子、峰值因子这6个无量纲参数作为辅助逆变电路特征参数，以兼顾不同程度软故障的敏感性和稳定性，并构造16种电路模式的特征向量。

表2列出了图1中电容在、、故障模式下的a、b、c相的电压信号的特征向量。

表2 三相电压信号时域特征参数值Tab.2 Time domain characteristic parameter value of three－phase voltage signal

3 模糊相似矩阵

3.1 获取数据

将不同模式下提取的时域特征参数设为一组特征向量。以为例，将a、b、c相电压信号的6个时域特征参数依次排列组成一个特征向量，剩余故障模式的特征向量依次设为，，…，，则｛，，…，｝为所有故障模式的特征向量集合，其中每种故障模式又由18个时域特征表示其性态，即x＝｛x，x，…，x｝（1，2，…，16），这样便得到了原始数据矩阵（x）。

3.2 建立模糊相似矩阵

在原始数据矩阵中，如果x与x的相似程度为r＝R（x，x），则称之为相似系数。确定相似系数是建立模糊相似矩阵的关键，相似系数表征了样本之间的相似程度。

本文选取欧氏距离法确定相似系数，具体方法如公式（1）所示：

其中，为使得所有r∈［0，1］（，1，2，…，16）的确定常数，可适当选取。

首先计算样本间欧氏距离，以样本为例，其与各样本间欧氏距离见表3。

表3 样本间欧氏距离Tab.3 Euclidean distance between samples

最终计算发现所有样本间欧氏距离均在区间0，1[ ]内，因此将取值为1。求得相似系数后，最终确定模糊相似矩阵如下所示：

4 竞争神经网络

4.1 竞争神经网络原理概述

竞争神经网络的竞争学习过程是对输入矢量的聚类过程。一个竞争神经网络的结构可分为输入层和竞争层，其中为其连接权值，如图3所示。

图3 竞争神经网络结构图Fig.3 Competitive neural network structure diagram

其基本计算方法如图4所示，输入向量和输入权值向量经过‖ndist‖计算，计算后输出是1维的列向量，列向量中各元素为向量与欧式距离的负数，之后再和一个阈值相加，得到作为竞争层传输函数的输入，此时中最大的元素即认为是竞争过程的获胜者，竞争层传输函数输出1，而其余元素输出均为0。

图4 计算方法图Fig.4 Calculation method diagram

4.1.1 Kohonen权值学习规则

针对权值向量，竞争神经网络采用Kohonen学习规则进行调整。假定第个神经元获胜，则输入权值向量的第行元素按式（2）调整，而其他神经元的权值不变。

其中，为学习率。

即前一个权值加上一个误差项，通过这一调整过程，一些靠近输入向量的神经元权值向量被修正到更加靠近，因此当获胜的神经元在遇到下一次相似的输入向量出现时，获胜的概率更高。从而在经过越来越多的训练学习后，每一个网络层中的神经元的权值向量很快被调整为最接近某一类输入向量的值，则具有相似输入向量的各类模式作为输入向量时就会获胜，即对应的神经元输出为1。

4.1.2 阈值学习规则

在竞争神经网络中，存在一些“死神经元”，这类神经元初始值偏离所有样本向量，无论训练多久始终无法获胜。

此时可以通过阈值调整，对一些输入向量与权值相似性不高的神经元赋予较大的阈值，使之具有获胜的可能。而对于经常获胜的神经元则赋予较小的阈值，这就意味着只有当输入向量与权值非常相似时神经元才会响应，对于从未获胜的神经元则不必如此。

4.2 竞争神经网络分类验证

按照表1设置的故障模式，运行图1所示仿真电路，并提取测点信号（输出端三相电压）的无量纲时域特征参数组成特征向量，在确定原始数据矩阵后计算样本间的相似系数，最终将求得的模糊相似矩阵输入竞争神经网络模型中，按照预设的正常状态、软故障以及失效状态这3种电路分类，将竞争层个数设为3，学习率设为0.1。同时，将原始数据矩阵输入相同的竞争神经网络分类模型进行对比，分类结果见表4。

表4 分类结果对比Tab.4 Comparison of classification results

在采用模糊相似矩阵作为输入时，16个样本特征成功分为了3类，30次训练后即可达到93.75%的准确率，与采用原始数据作为输入相比减少了一定的训练次数。

竞争神经网络经过对样本模糊相似矩阵的学习，已经大致具备了识别相似样本的能力。接下来选取不同的电容的样本集，即电容的电路状态样本的模糊相似矩阵，放入模型中进行分类验证，结果见表5。

表5 分类验证结果Tab.5 Classification verification results

选取的两组正常状态下样本对应的故障模式、在第2竞争层获胜，选取的两组软状态下样本对应的故障模式、在第3竞争层获胜，符合实际电路模式。因此，建立的竞争神经网络模型能够准确识别电路状态识别。

5 结束语

本文提出一种基于时域参数的样本特征提取，结合模糊聚类方法建立全体样本特征的模糊相似矩阵并采用竞争神经网络模型对滤波电容进行状态分类，实现了对地铁车辆辅助逆变器中滤波电容软故障的诊断以及对电路状态的分类。针对辅助逆变电路的状态识别，提出了基于时域参数的特征提取方法，选取无量纲时域参数构造特征向量，能直观地表征测点信号的结构特点并且计算量小，无需复杂的变换与分解；参考模糊聚类方法，利用欧氏距离计算出电路故障模式样本间的相似系数，并建立模糊相似矩阵，对原始数据进行处理；利用竞争神经网络进一步实现电路状态的分类，并分别对模糊相似矩阵以及原始数据进行分类对比，在采用模糊相似矩阵作为输入时可减少训练次数，最终的分类验证结果与实际电路故障状态符合。