基于GPS数据的震前短临异常检测

李 南，林莉莉

（福建农林大学 计算机与信息学院，福州 350000）

0 引 言

震前短临异常检测已成为防震减灾研究与应用领域的研究热点。当前，国内外学者大多采用射出长波辐射、电离层电子总含量等电、热指标，来进行短临异常检测，以探测震前一段时间及一定区域内可能发生的地球物理、化学变化。但这些方法普遍存在观测数据不足、容易受到人为活动干扰等缺陷。

近年来，随着全球导航卫星系统技术（Global Navigation Satellite System，GNSS）的发展和GPS台站的普及，利用GPS数据进行短临异常检测已成为热门研究方向。与传统的电、热指标相比，利用GPS数据的方式，能更直接观测到大地震发生前出现的地表中、低频地形形变，具有较好的客观性和稳定性。但是，现有大多数研究方法普遍依赖地理学科领域专家的知识和经验，且仅用单个典型震例的GPS数据来验证异常检测方法的有效性，使其存在主观性较强、普适性较差等问题。

鞅理论作为现代概率和随机过程的基础，适用于时间序列数据分析场合，已被广泛运用于数据挖掘中的决策优化、异常检测等领域。因此，本文结合数据挖掘的相关知识，运用鞅理论，提出一种基于GPS数据的震前短临异常检测算法（Anomaly Detection Algorithm based on GPS data，ADA）。

实验结果表明，ADA算法所识别的GPS数据中异常出现时间与地震发生时间存在显著相关。相比于传统的准则分析方法、异常检测模型ARIMA、单类别支持向量机OCSVM，以及基于两阶段聚类的异常检测算法TSOD等，ADA算法能够更直观、准确地反映震前GPS数据中出现的异常，可为地震预警减灾提供有效手段。

1 研究方法

本文短临异常检测算法包括：数据预处理、特征提取以及异常检测3部分内容。

1.1 数据预处理

由于数据采集设备、传输线路故障等原因，各GPS台站的原始数据存在部分数据缺失的情况。另外，GPS台站每日坐标包括东西、北南和垂直3个方向的数据，但垂直向数据通常误差较大。因此，本文仅针对各GPS台站东西向和北南向的坐标数据进行处理。

首先，采用二阶多项式拟合方法，依次对东西向和北南向上的GPS数据进行缺失值填补。

1.2 特征提取

当同一个震例涉及多个GPS台站，且不同台站之间GPS数据出现异常的时间和强度存在较大差异时，会导致异常检测结果出现较大偏差。为了弥补以上不足，本文基于同一震例的所有相关GPS台站数据，采用二阶多项式拟合方法估算相应震例震中位置的每日坐标。震中坐标估算过程如算法1所示。若某一震例只涉及一个台站，则直接使用该台站数据即可。

使用所有相关GPS台站的数据，估算震中位置的每日坐标（以东西向为例）。

震中位置的经度x，相关的个GPS台站的经度，，…，x，相邻两日各台站东西向坐标偏移量，，…，Δx。

震中东西向的每日坐标。

针对各台站每日坐标位移数据(x，Δx)，1，2，…，，求解出使得二项式拟合函数的损失函数最小化时的权重。

基于拟合函数(，)，输入震中位置的经度x，获得估算的偏移量( x，)。

根据x和(x，)，得到预估的震中东西向的坐标x＋y（x，）。

为了降低GPS数据中白噪声、高斯噪声等对检测结果的影响，在运用算法1获得震中位置各方向的时序坐标数据后，使用滑动窗口技术对数据进行降噪处理。固定大小的滑动窗口内样本数据斜率的变化，不仅能有效刻画数据在长趋势变化下的短期特征，而且对噪声具有一定的鲁棒性。因此，本文使用GPS台站东西向和北南向坐标数据的斜率变化范围来提取震中每日的综合特征。特征提取过程如算法2所示。

根据震中东西向、北南向的每日坐标（见算法1），提取震中的每日综合特征。

震中东西向、北南向的每日坐标（）、（），滑动窗口大小_。

震中第天的综合特征（）。

使用线性回归算法，计算第天前_天内东西向、北南向坐标：

（）：_≤≤以及（）：_≤≤的斜率，记为S（）、S（）。

计算滑动窗口内，斜率S（）、S（）的变化范围：

计算震中第天的综合特征值：

1.3 异常检测

地震的发生通常需要一定时间的能量累积，本文基于提取到的某震中综合特征值，评估该震中第天的短临异常程度，并在此基础上利用鞅理论评估震中在某连续时间段内短临异常程度。

设：C为前1天综合特征{，，…，V}的均值（即中心值），即：

D为V相对于C的偏移程度，即：

其中，‖·‖表示欧式距离。

根据公式（2）得到的偏移程度，进一步计算V和{，，…，V}之间的相异度值S，即：

其中，是一个(0，1]之间的随机数，（）是一个函数，返回满足指定条件数据的数量。

如：( j｜D＞D)表示在｛，，…，V｝中D＜D，1，2，…，的数据数量。

从公式（3）可以看出，S∈(0，1]。根据同一分布中各样本差异最小化原则，S越小V就越远离前1天数据的中心值C，则V和{，，…，V}之间越不相似，表明震中第天的短临异常程度越高。

鞅理论适合于刻画时间序列数据的连续变化情况，使用统计量幂鞅值，可对持续一段时间内数据的异常程度进行量化。幂鞅值越高，越倾向于拒绝接受数据序列分布稳定的假设。本文采用鞅理论对数据{，，…，S}的分布情况进行量化分析，得到天内{，，…，S}的幂鞅值M。

其中，S为V和{，，…，V}之间的相异度值，根据文献［1］的推论取值0.82。

从公式（4）可见，幂鞅值M值越大，说明天内频繁出现值较小的情况，暗示t天内GPS数据频繁出现异常的程度越高。为了避免公式（4）中幂鞅值M值无限增大，需引入一个停止参数作为M的阈值。此外，本文还引入一个稳定参数_，从第_1天开始计算幂鞅值，以避免过短的时间序列数据对分析结果造成误差。异常检测算法具体过程如算法3所示。

使用某震中的综合特征序列，计算该震中t天内的幂鞅值M。

某震中的综合特征{，，…，V}、停止参数、稳定参数_。

某震中天内的幂鞅值M。

设：_1。

根据{，，…，V}，采用公式（1）、（2）分别计算，得到C和D。

根据C和D，采用公式（3）计算S。

根据S，采用公式（4）计算M。

如果M≤，则1，重新执行步骤25，否则将第1天作为第1天，重新执行本算法。

1.4 ADA算法流程

基于算法1、算法2和算法3，则ADA算法具体流程如图1所示。

图1 ADA算法流程图Fig.1 Flow chart of ADA algorithm

2 实验设计与分析

2.1 实验数据

本文研究对象为2001～2010年间，北美发生的震源深度小于60 km且震级大于6.0级的地震。GPS台站时序坐标数据来自Nevada Geodetic Laboratory提供的数据共享服务网站（http：／／geodesy.unr.edu／）。选择的GPS台站，需处于受相应地震孕育影响的范围（即震中半径10之内，表示地震震级，的单位是km）。实验选择位于影响范围内，最靠近震中的10个GPS台站。由于地震孕育过程通常在地震前1～30天开始，因此所使用台站的数据从地震发生前180天开始，到后30天结束。为了确保有足够的台站以供分析，单个台站在这段时间内最多允许5%的数据缺失。从平台获得的数据是初步处理后的GPS台站每日坐标分别是东西向、北南向和垂直向。文献［3］中证实，GPS台站的时序坐标数据在垂直方向的测量误差远大于水平方向。因此，实验中只选用东西向、北南向的每日坐标作为研究数据，以保证分析结果的可靠性。

综合考虑GPS台站位置和数据完整性，本文最终采用的震例数据见表1，相关信息来自美国地质调查局网站（https：／／earthquake.usgs.gov／）。

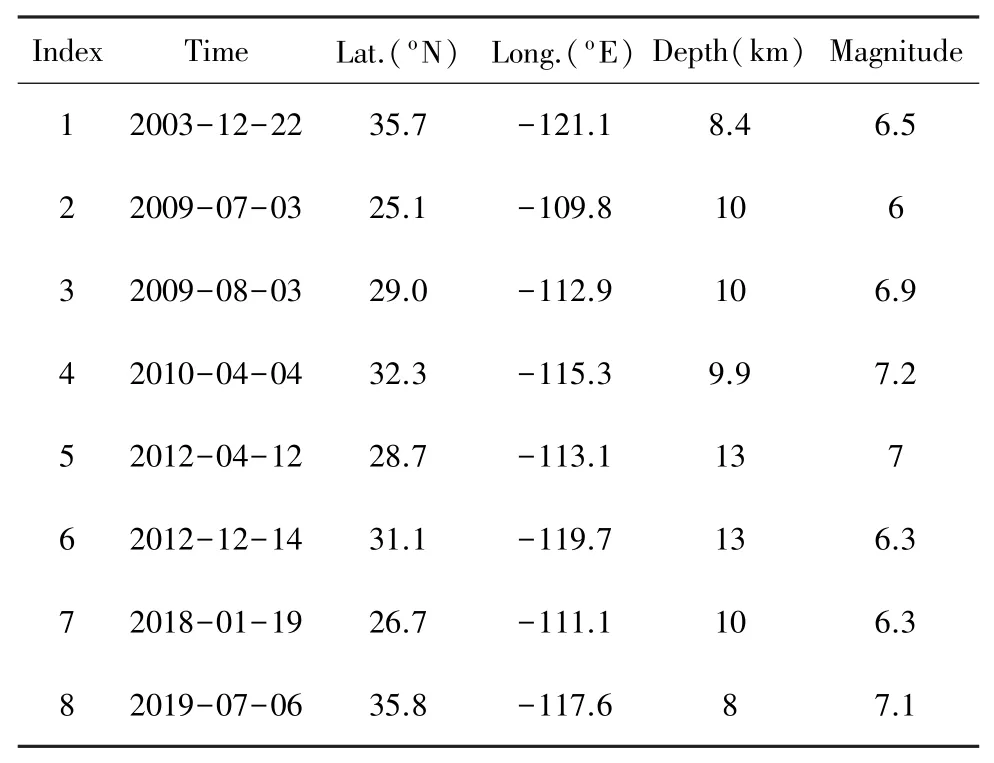
表1 震例数据Tab.1 Earthquake data

2.2 对比算法与参数设置

为了验证基于GPS数据的短临异常检测算法的有效性，将本文的ADA算法与传统的准则分析方法、异常检测模型ARIMA、单类别支持向量机OCSVM以及基于两阶段聚类的异常检测算法TSOD进行性能对比。

（2）ARIMA模型：利用差分整合移动平均自回归模型，得到一个预测值，通过预测值与实际值的误差大小来判断异常位置。本文ARIMA模型中的信息准则函数选用贝叶斯信息准则。

（3）OCSVM：单类别支持向量机，将异常检测视为特殊的分类问题。在训练过程中，只有一类数据，首先得到可以代表这部分数据的模型。在检测过程中，判断给定样本是否属于此类别。本文OCSVM算法中的核函数选用高斯核函数。

（4）TSOD算法：是基于两阶段聚类的多变量时间序列异常检测算法。第一次聚类在各个变量上筛选初始异常时间，第二次聚类结合所有变量进行异常定位，以降低误检率。TSOD算法中第一次聚类使用基于混合高斯模型的EM算法，第二次聚类使用以全连接方式度量的层次聚类方法。

对比实验和参数优化实验中，使用的数据来自表1中震级最大的2010－04－04地震，准则、ARIMA模型、OCSVM以及TSOD算法仅使用距离地震震中最近的编号为P500的单个GPS台站（Latitude：32.69N，Longitude：-115.30E）数据。本文ADA算法则涉及多个台站的GPS数据，停止参数设置为2 000，窗口大小_设置为7，稳定参数_设置为5。

2.3 性能对比分析

图2～图4、表2和图5分别给出了准则、ARIMA模型、OCSVM、TSOD算法以及ADA算法的运行结果。

表2 P500台站使用TSOD算法分析结果Tab.2 Analysis result of TSOD algorithm on P500 station

图2 P500台站各向kσ准则分析结果Fig.2 Analysis result of kσmethod on P500 station

从图3（a）～图3（b）可见，震前45天左右，P500台站东西向和北南向的坐标出现了ARIMA模型的预测值与真实值误差较大（即异常）的情况，但随着地震的临近，误差并没有继续保持在较高的水平。因此，不能完全确定此次异常是否与地震相关，也可能与噪声有关。在垂直向上，ARIMA模型的预测值和真实值之间的误差并没有显现出任何规律，这同准则的分析结果相一致。

图3 P500台站的ARIMA模型分析结果Fig.3 Analysis result of ARIMA model on P500 station

图4（a）～图4（c）中，横坐标表示时间，纵坐标表示当天给定方向的坐标值，在OCSVM算法下的类别。1表示正常，－1表示异常。从图4（a）可看出，P500台站东西向异常最早出现在震前45天左右，在一周后断断续续出现并延续到震前。从图4（b）～图4（c）可看出，OCSVM算法在北南向和垂直向上，震前没有发现明显的异常显现规律，并出现多次误报。异常的不持续以及3个方向上异常出现时间的不统一都增加了结果分析的难度。

图4 P500台站的OCSVM算法分析结果Fig.4 Analysis result of OCSVM algorithm on P500 station

从表2可以看出，TSOD算法在P500台站GPS数据上，最终检测出3次异常。其中，距离地震发生最近的异常是在震前40天左右（2010－02－25），并出现了两次明显的误报（在2009－12－22以及2010－01－28）。

图5给出了2010－04－04地震ADA算法运行结果（即幂鞅值的变化趋势）。从图5可明显看出，在震前绝大部分时间，幂鞅值始终保持在一个相对较小的区间内。由于大地震震前能量是一个累积的过程，幂鞅值从地震前较短的一段时间（约1个星期）开始缓慢增加，说明GPS数据开始出现异常，暗示震前局部应力场开始调整。地震后各个台站的坐标发生了较大变化，因此幂鞅值的波峰是在地震后出现，且在地震后迅速超过预设的阈值。这说明ADA算法对2010－04－04地震的异常检测是有效的，且比4种对比算法能更直观地反映出震前短临异常，不易出现误报的情况。

图5 2010－04－04地震的ADA算法运行结果Fig.5 Analysis result of ADA algorithm on 2010－04－04 earthquake

2.4 参数优化分析

2.4.1 稳定参数分析

为了分析稳定参数_对本文方法性能的影响，在2010－04－04地震上分别将_设置为5、7和9进行实验，幂鞅值的变化趋势如图6所示。

图6 基于不同稳定参数的ADA算法结果Fig.6 Comparison of result with different stable_day

从图6可看出，不同的_参数值，并不会对检测结果造成太大影响。不同取值下，幂鞅值的变化趋势均表现为在地震前较短的一段时间内开始增加，并在地震后的一段时间内达到波峰。这是由于当地壳运动相对稳定时，前_天的GPS数据并不会发生太大变化，因而对结果的影响不大，不同取值下幂鞅值波峰出现的时间仅差距1～3天。但当参数为5时，幂鞅值最早出现增加的趋势。据此，实验中将稳定参数_设置为5。

2.4.2 平滑窗口分析

为了分析平滑窗口大小_对本文方法性能的影响，在2010－04－04地震上分别将_设置为5、7和10进行了实验，幂鞅值的变化趋势如图7所示。

图7 基于不同平滑窗口的ADA算法结果Fig.7 Comparison of result with different window_size

当平滑窗口_的取值较小时，在特征提取阶段，计算第天的综合特征值所需要的样本数就越少，因此更容易受到单个样本的影响，对异常的检测也更敏感。从图7可看出，对比_7和_10，当_5时，在地震发生前一个月就出现了幂鞅值缓慢增加的趋势，相应幂鞅值的波峰也在地震发生前最早出现。而对于_7和_10，幂鞅值开始增加和波峰出现的时间并不存在显著差别。因此，为了提高算法的鲁棒性，实验中将_设置为7更为合理。

2.4.3 停止参数分析

为了分析停止参数对本文方法性能的影响，在2009－07－02地震上分别将设置为500、1 000和2 000进行了实验，幂鞅值的变化趋势如图8所示。

图8 基于不同停止参数的ADA算法结果Fig.8 Comparison of result with different h

从图8可看出，对于2009－07－02地震，3种停止参数设置下，幂鞅值均在地震发生前较短一段时间内显著提高，这与文献［1］中的结论相一致，即孕震活动最早在震前30天左右开始，并在震前几天内表现最为活跃。值得注意的是，当参数设置为较小（500）时，幂鞅值的波峰多次出现，会导致异常的误报。当检测到GPS数据出现震前异常时，幂鞅值仅经过一天就从小于1 000增大到2 000以上。因此，参数1 000和2 000的幂鞅值曲线几乎重合。由于较大的停止参数会减少预警时间，降低误报可能，实验中将设置为2 000。

2.5 显著性检验

为了验证ADA算法所识别的GPS数据中存在的短临异常与对应地震之间存在关联，本文使用Molchan图表法，在表1所示的8个震例上进行了统计显著性检验，结果如图9所示。

图9 8个震例的Molchan图表分析结果Fig.9 Analysis result of ADA algorithm oneight earthquakes by Molchan error diagram

图9中，横坐标表示时间占有率，纵坐标表示相应的漏报率，使用的方法相比于随机预测的优劣程度以曲线与图表边界线所包围的面积来衡量，面积越小则说明预测效果越好。若测试的结果接近于图9所示的对角线，则表示预测方法无统计显著性。实验中，若幂鞅值波峰出现在第天，那么将前天和后天作为变量，即以［，］作为预警时间范围。若地震发生在此时间段内，则表示预警成功。通过调整和的取值以绘制图表。从图9中可以看出，ADA算法的时间占有率－漏报率曲线远在对角线之下，说明所识别的短临异常与对应地震之间存在显著性关联。

3 结束语

震前短临异常检测是地震预警减灾的关键。本文提出的ADA算法能够弥补现有方法存在的主观性较强、普适性较差的问题。8个震例的实验结果证实了ADA算法检测到的短临异常与地震之间存在显著相关。另外，本文也对算法的参数进行了优化分析。

然而，地震监测预警是一项复杂的任务，会涉及与孕震相关的岩石圈－盖层－大气层－电离圈层等多个数据源。因此，如何结合这些异源数据来进行异常检测是下一步的研究方向。