基于Hankel 矩阵填充的稀疏孔径ISAR 成像

彭鑫鑫，张邦杰，李浩林，盛佳恋，江利中，徐 刚

（1.东南大学 毫米波国家重点实验室，江苏 南京 210096；2.中国空间技术研究院，北京 100098；3.上海无线电设备研究所，上海 201109）

0 引言

作为一种全天候、全天时的微波遥感工具，逆合成孔径雷达（Inverse Synthetic Aperture Radar，ISAR）在民用和军用领域都有着广泛的应用。为了获得二维高分辨率图像，ISAR 不仅需要在发射机上发射宽带信号以获得距离维高分辨率，同时也需要依靠雷达和目标之间较大的视角变化来获得方位维高分辨率。具体来说，方位维的分辨率取决于因目标运动而引起的雷达与目标之间的相对角度变化，即在相干处理时间（Coherent Processing Interval，CPI）内形成的合成孔径。分辨率是成像雷达的一项极其重要的指标，更高的分辨率可以得到更多的目标信息。随着雷达技术不断飞速的发展，雷达能够实现的任务也更加多样化，包括成像、定位、跟踪等。多功能雷达通过转换为不同模式来实现不同的功能需求。由于多功能雷达工作状态交换、观测目标进行非协同机动运动等不可避免的因素存在，在一些实际应用中只能对目标进行稀疏孔径（Sparse Aperture，SA）测量。通过SA 测量得到的稀疏回波直接进行距离-多普勒（Range-Doppler，RD）成像，所得结果的方位维会产生严重模糊，使得ISAR 成像的结果与观测目标有很大的差异。

目前已有的一类稀疏孔径ISAR 成像方法是基于稀疏先验信息的压缩感知方法。通过对ISAR 图像稀疏表征，压缩感知方法可实现稀疏孔径非模糊成像。然而，现有的压缩感知类方法在进行稀疏重构时，不可避免地会使用离散字典对信号进行稀疏表示，这类方法往往会因为模型不匹配而导致恢复误差，是其固有缺点。相比较而言，矩阵填充（Matrix Completion，MC）不仅可以突破对数据的采样限制，还可以直接进行稀疏数据重构以避免直接成像引入的模型匹配问题。近年来，矩阵填充理论被引入到雷达成像应用中，只要被随机观测的矩阵具有低秩特性，就可以通过矩阵填充技术实现雷达高分辨成像。从本质上看，相较于使用离散字典的CS 方法，MC 方法没有离散失配的问题，可被归类为无网格技术。此外，还可以通过将得到的SA 回波构造成Hankel 结构来增强矩阵的低秩特性，从而获得更好的MC 性能。

本文提出了一种基于Hankel 矩阵填充的稀疏ISAR 成像方法。根据每个距离单元的回波数据构建Hankel 矩阵。然后对构造的Hankel 矩阵的低秩性质进行了验证，为方位维成像提供先验信息。最后，对基于增广拉格朗日乘子（Augmented Lagrange Multiplier，ALM）的Hankel 矩阵填充进行逐步迭代求解，从而实现方位维成像。本文所提出的算法能够克服CS 方法中的固有缺点，即因为模型不匹配导致恢复的二维图像在方位维上仍然存在较大误差。最后，使用实测数据进行了实验验证，通过比较Hankel 矩阵填充与全孔径成像结果的拟合度，确认所提出算法的有效性。

1 信号模型

1.1 ISAR 成像信号模型

典型的ISAR 是在观测时间内雷达位置保持不变，目标发生运动。ISAR 通过距离-多普勒算法处理来自运动目标的回波，实现对运动目标的成像。在实际应用场景中，观测的运动目标的尺寸要远大于发射波长，即目标位于雷达光学区，从而运动目标表面的散射特性保持稳定。将观测的运动目标近似为由多个散射点组成，当雷达发射宽频带信号且雷达与目标之间发生相对运动时，可同时实现距离维和方位维的分辨率成像。在目标与雷达的观测视角发生变化的过程中，目标中存在的较强方向性部件会导致散射点的分布发生变化。对于ISAR 成像，在视角变化较小的情况下（一般为3°～5°左右），散射点在目标上的位置和强度可视为不变，即目标散射系数和散射点位置不变。在这种情形下，ISAR 可应用散射点模型表示观测目标，通过距离-多普勒算法得到目标高分辨率图像。

雷达与目标之间的相对运动包括平移运动和旋转运动。假设已完成精确稳健的平动补偿，即可用转台模型解释ISAR 的成像几何，如图1所示。

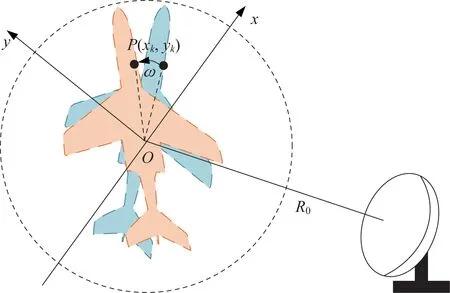
图1 ISAR 成像几何Fig.1 Geometry of ISAR imaging

在图1 转台模型中，将参考点视为在CPI 内保持静止的点。假设观测目标由个散射点组成，并以恒定角速度围绕参考原点做旋转运动，那么，在远场假设下散射点p(x，y)相对雷达的距离在慢时间域下可以表示为

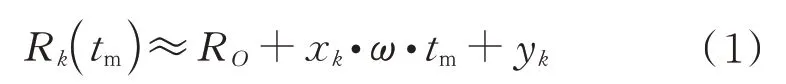
式中：R为参考点到雷达的距离；x、y分别为散射点p在转台模型中的横坐标和纵坐标。

基于散射点模型，所有个散射点叠加后的接收回波信号可以写为

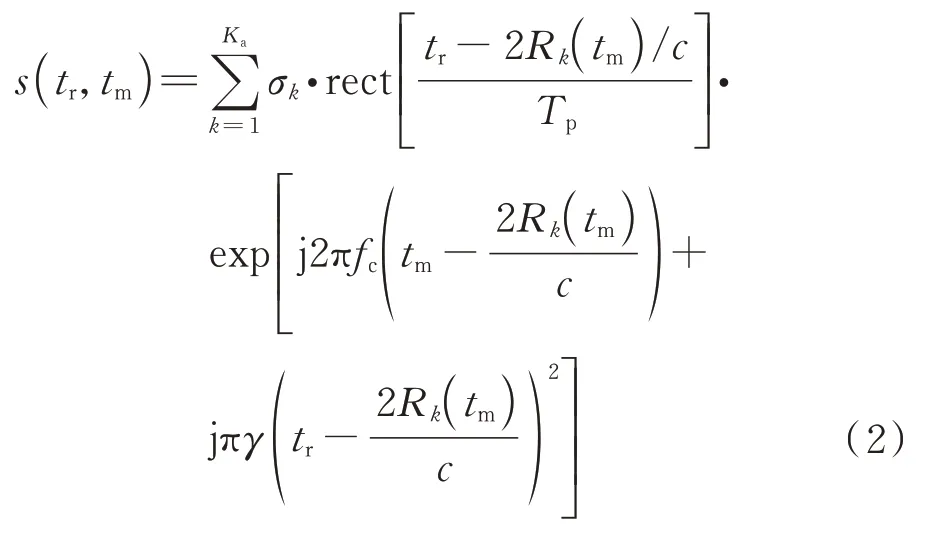
式中：雷达发射的宽带信号为线性调频（LFM）信号；σ为散射点p的散射系数；为电磁波在真空中的传播速度；为快速时间，全时间=+；、和分别为LFM 信号的脉冲宽度、中心频率和调频率。

需注意，由于目标转动角度较小，本文假设这里的旋转运动并没有产生越距离徙动（MTRC）。在完成匹配滤波、包络对齐和相位校正后，距离维脉冲压缩后的数据可以表示为

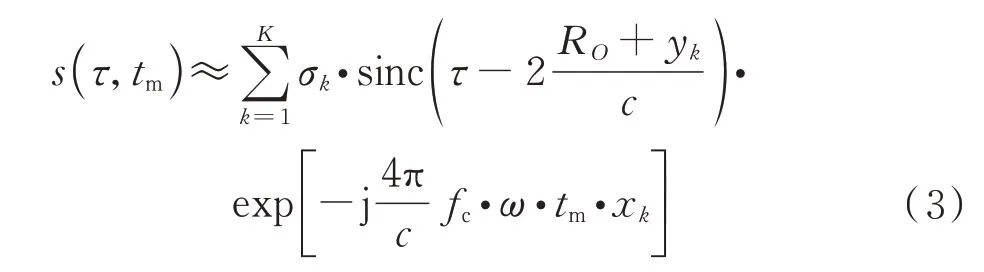
该公式忽略了一些常数相位项，为距离维脉冲压缩后的快时间。式（3）的离散形式可以表示为

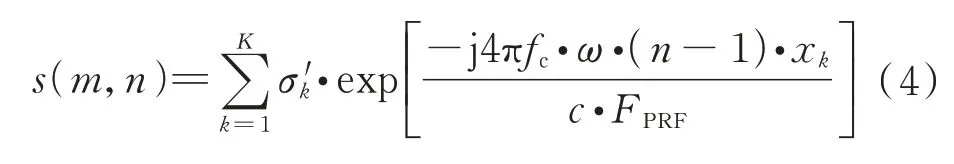
式中：为雷达系统的脉冲重复频率；=1，2，…，和=1，2，…，分别为快时间域 距离维和慢时间域方位维的指数。

在全孔径情况下，可以直接应用二维傅里叶变换获得ISAR 高分辨图像。在SA 下得到的目标回波信号具有稀疏性，因此可以先进行矩阵填充，然后得到二维成像。

1.2 低秩特性分析

对于第个距离单元，式（4）中距离维脉冲压缩后的数据可以用向量形式表示为

式中：为束参数。

为了说明所构建矩阵的低秩特性，可将该Hankel 矩阵进行范德蒙分解：

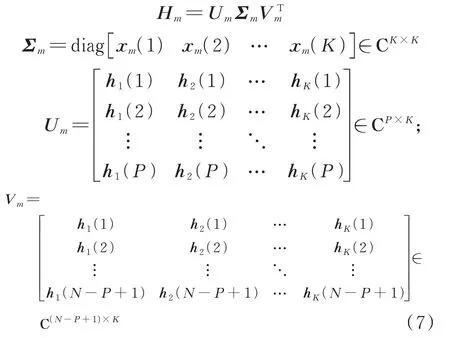
观察范德蒙分解可以看出，H的秩以为界。因此，基于稀疏孔径回波构造的Hankel矩阵是低秩的。

2 所提出的矩阵填充稀疏成像方法

利用第1 章中证明过的低秩特性，即可将稀疏孔径成像问题转化为低秩Hankel 矩阵的重构问题，即

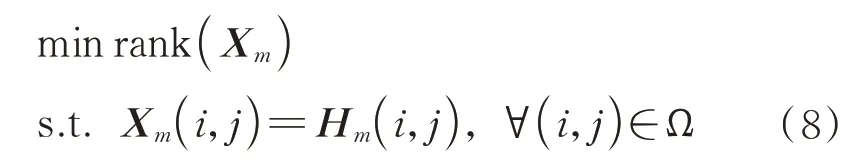
式中：X为待求的矩阵，其在观测位置(，)∈Ω处元素与H相同，而在稀疏孔径位置处的元素被设置为0。利用ALM 算法多次迭代来求解该问题。

首先，通过核范数最小化来替换秩最小化问题，从而将MC 问题表述为

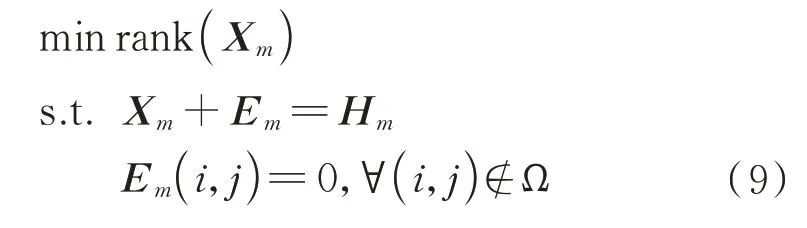
然后，可以通过最小化增广拉格朗日函数进行求解，从而获得全孔径回波

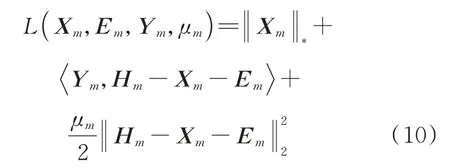
式中：X为要求解的结构化低秩矩阵；E为H的未知项为零的矩阵；μ为一个给定的正数；Y为对偶变量。

整个算法流程如图2 所示。

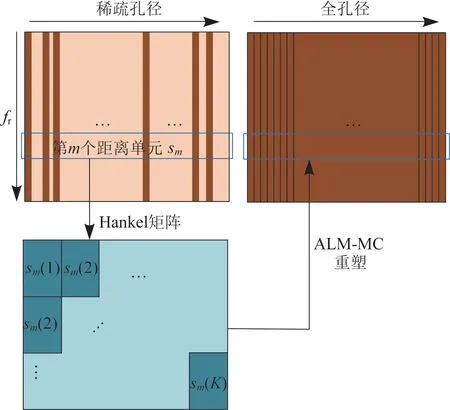
图2 算法流程Fig.2 Flow chart of the proposed algorithm

接下来，可以通过迭代计算每一步的优化问题来最小化目标函数(X，，，)。具体来说，主要步骤如下所示：

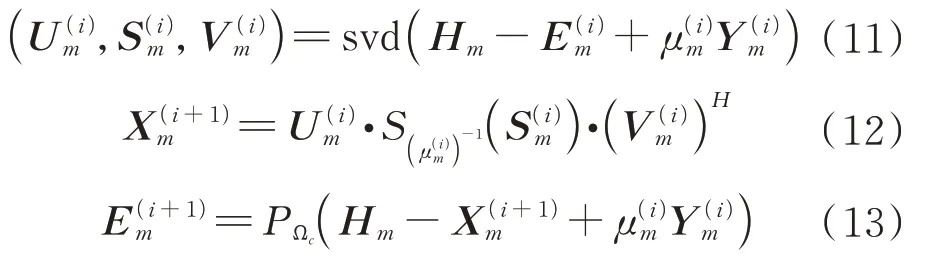
式中：svd(·)为奇异值分解操作；(·)为软阈值操作；(·)为向区域Ω 投影。

算法流程如下。

最后，对本文所提算法的运算复杂度进行分析。所提算法的主要运算量在于式（11）和式（12）的求解：式（11）中矩阵奇异值分解的计算复杂度为(+·)，式（12）中矩阵乘积的计算复杂度为(·+(-+1)·)。假设所提ALM算法的循环迭代次数为，个距离单元，那么所提算法的运算复杂度为(··(·+(-+1)·))。

3 实验分析

使用Yak-42 飞机的实际测量数据来验证所提方法的性能。文中实验均在Matlab R2021b 版本软件实现，所用计算机主频2.1 GHz，内存16 GB。该雷达系统中心频率为5.52 GHz，发射信号带宽为400 MHz，脉冲重复频率（Pulse Repetition Frequency，PRF）为400 Hz。实验中使用了256 个距离采样和256 个脉冲。在进行实现前首先对该数据进行了包络对齐和相位自聚焦，使用均方根误差（Root Mean Square Error，RMSE）和相关系数（Correlation Coefficient，CORR）作为评估图像质量的指标，定义为

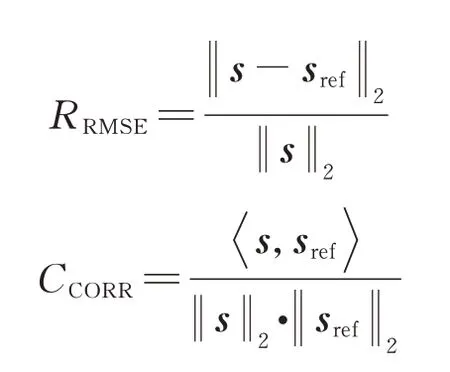
式中：=vec() 为矢量化的SA 图像；=vec()为在全孔径下的参考图像。

使用本文所提出方法得到的图像如图3（a）所示，基于L1范数约束的CS 方法的图像如图3（b）所示，作为参考的全孔径距离多普勒算法的结果如图3（c）所示，0.5 稀疏率下的随机SA 模式如图3（d）所示。不同方法得到的图像之间的差异用红色虚线表示。

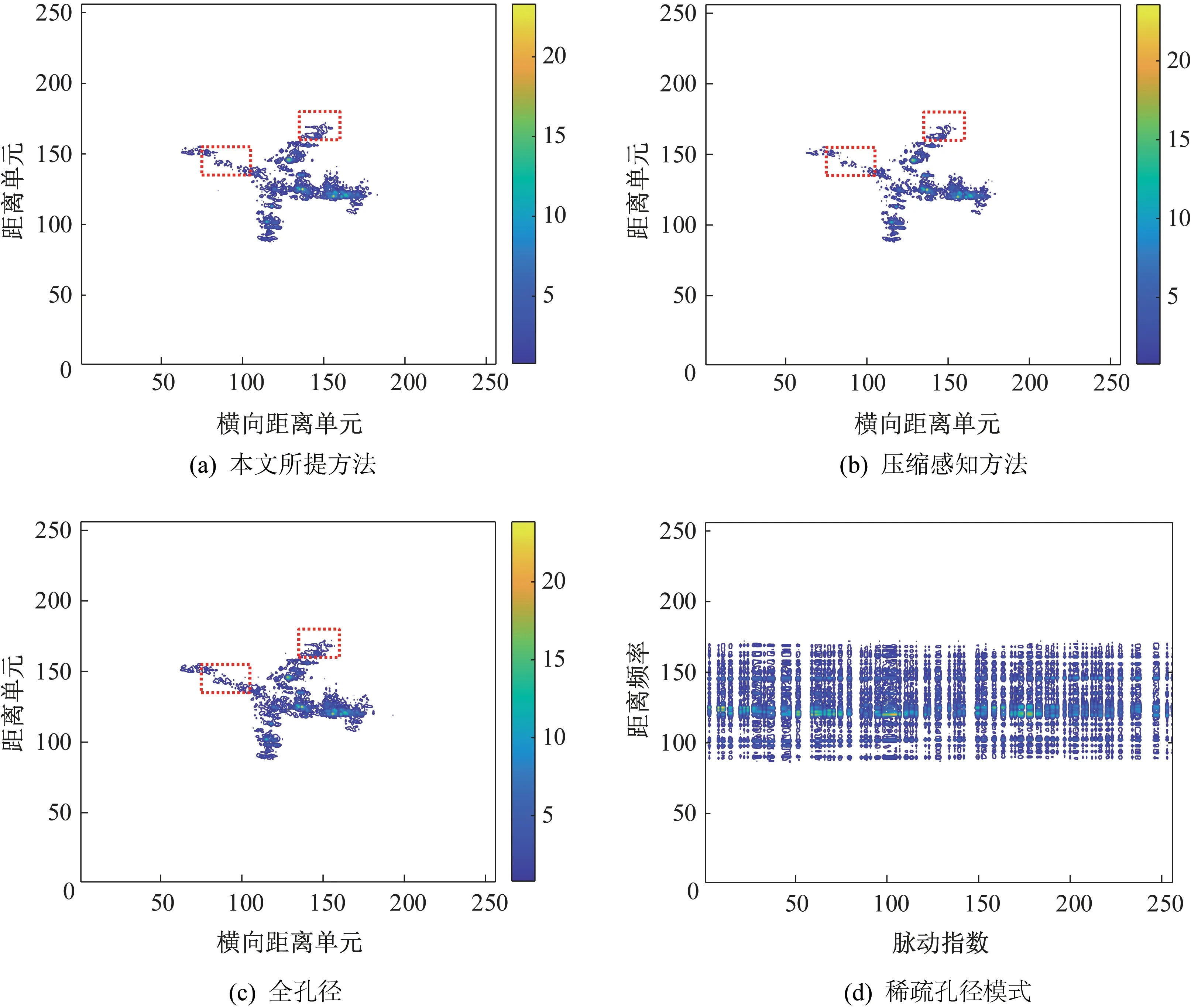
图3 使用不同方法的性能表现Fig.3 Performance images with different methods

在图3 中，在稀疏率为0.5 的情况下，直接使用稀疏孔径得到的回波进行二维成像的效果是很不理想的，方位维产生严重模糊，R-D 算法结果与运动目标严重不匹配。Hankel 矩阵填充和CS 方法在低稀疏率下都可以弥补由SA 引起的方位维的模糊性。通过与全孔径参考图像结果对比，两种算法的成像结果与运动目标具有很高的一致性。此外，通过对比所提方法与CS 算法的成像结果可知，本文所提方法的成像结果与全孔径参考图像具有更高的一致性。

比较两者的运行程序时间：本文所提算法用时70.27 s，CS 算法用时18.74 s，两者基本在一个数量级（需要说明的是，两个算法均是未优化版本，其中CS 算法利用快速傅里叶变换，具有较高的运算效率）。

为了更细致地观察不同算法在SA 下的成像的准确性，本文选择了一个距离单元，观察该距离单元内的散射点在不同的方位维单元的脉冲响应恢复结果，细节如图4 所示。可以看到本文所提方法（Proposed）的恢复结果接近全孔径，表明所提出方法的有效性和准确性。结合实验结果可知，由于所提算法做的是全孔径数据补全，其稀疏孔径成像分辨率不会超过理想情况下全孔径分辨率，其极限情况对应全孔径分辨率。

图4 第125 距离单元方位维度上某一散射的脉冲响应Fig.4 Pulse response of a certain scatter in the crossrange dimension of the 125th range cell

此外，为了定量分析各算法的性能，本文通过20 次蒙特卡罗模拟进一步评估了所提出方法在0.1到0.8 的不同稀疏采样率（步长为0.1）下的性能，得到的RMSE 和COOR 的变化如图5 所示。通过定量结果分析，相较于SA 和CS 方法，本文所提出的方法具有最低的RMSE 和最高的COOR，证明MC方法优异的性能。

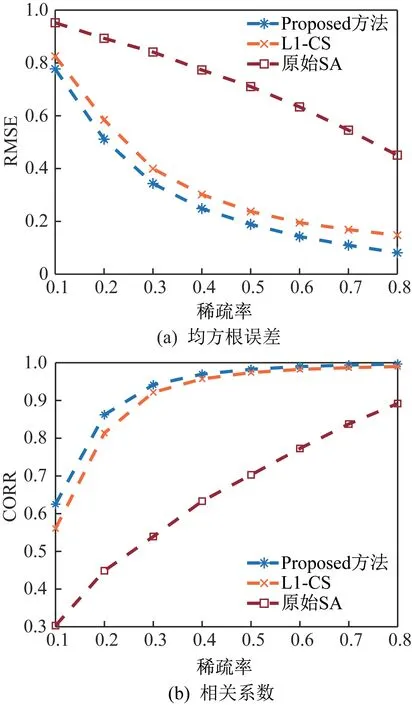
图5 不同稀疏率下性能Fig.5 Performance versus the sparse rate

4 结束语

本文基于稀疏孔径ISAR 成像方位维模糊，提出了一种无网格的Hankel 矩阵填充方法。相较于传统CS 方法，本文所提方法的成像结果误差更小，与全孔径成像一致性更高，在不发生离散模型失配的情况下弥补由SA 引起的模糊并获得高分辨率图像。最后使用实测数据进行了性能测试，证明了所提出算法的有效性和优越性。