一种顺轨干涉SAR 时变平地相位去除方法

孙 颖，吴思利，王 辉

（1.上海卫星工程研究所上海市毫米波空天信息获取及应用技术重点实验室，上海 201109；2.上海航天技术研究院毫米波成像技术重点实验室，上海 201109）

0 引言

合 成 孔 径 雷 达（Synthetic Aperture Radar，SAR）是主动式微波成像雷达，相比光学传感器具有全天候、强穿透等优点。如今，SAR 在军事和民用的诸多领域都发挥着重要作用。而基于SAR图像数据能够进一步实现高分辨率雷达信息应用，典型有基于空间角差异的干涉SAR 测绘和基于时间基线的动目标指示（Moving Target Indication，MTI），后者通常会在多组数据之中提取多普勒信息、位置、时间的关联特性，完成速度反演。

MTI 的主要技术途径包括了空时自适应处理（Space-Time Adaptive Processing，STAP）、偏置相位中心天线技术（Displaced Phase Center Antenna，DPCA）、顺轨干涉SAR（Along-Track Interferometric Synthetic Aperture Radar，ATI-SAR），后两者可以视做是STAP 的变体。顺轨干涉技术由于其更灵活的基线配置，已经经历了广泛的天基、空基应用，通过利用沿航向布置的天线得到的两幅或两幅以上具有相干性的SAR 复图像进行联合处理，实现地面运动目标检测及洋流监测等功能，具有十分重要的应用价值。成功的天基应用任务有航天飞机雷达地形测绘任务（The Shuttle Radar Topography Mission），使用单一混合基线完成了流场测量。德国的ROMEISER 等深入研究了星载顺轨干涉洋流检测，量化分析测量精度，并应用于TerraSAR-X 数据。

应用顺轨干涉技术的任务包括了在理想情况下，静止目标干涉相位为零，而运动目标干涉相位不为零。但由于平台和天线相位中心的不稳定，干涉基线的倾角变化会导致时变的交轨基线分量，从而引入平地相位干扰运动目标的检测和测速。现有的平地相位去除方法有基于地面控制点与敏感度方程的平地相位去除方法、基于干涉相位的平地相位盲估计方法。前者由于需要布设地面控制点实施成本和难度较大，后者则存在运算复杂度或地形适应性的问题。

本文提出一种基于回波数据的时变平地相位去除方法。该方法通过最小二乘法估计出基线在平地相位中的影响系数，再反演出估计的平地相位值，从而在干涉相位中进行去平地相位，具有较高的估计精度和效率，提升了运动目标的检测和测速性能。最后通过仿真实验验证了理论公式的正确性，并分析了平地相位估计误差。

1 ATI-SAR 基本原理

图1 ATI-SAR 动目标成像几何模型Fig.1 Geometric model of moving target imaging by ATI-SAR

假设ATI-SAR 两天线交替自发自收信号。根据几何关系，在方位时刻，两天线相位中心到运动目标的瞬时斜距分别为

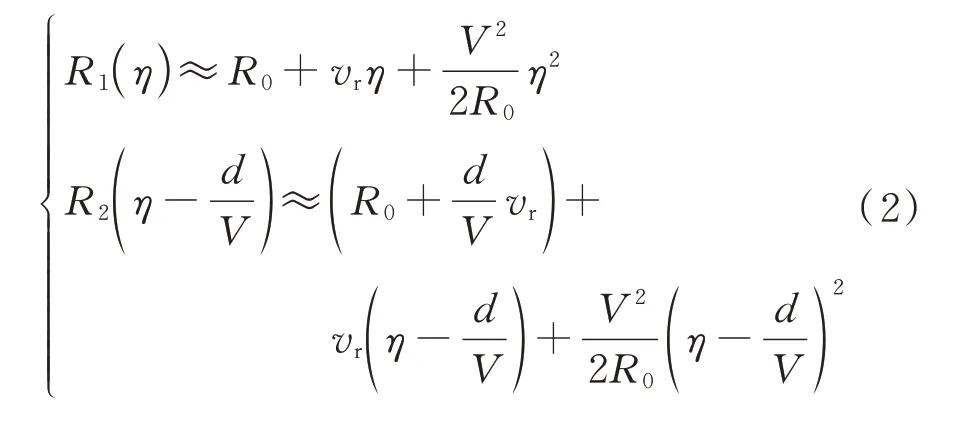
两天线接收的SAR 回波信号经过成像算法聚焦后，可以分别得到2 幅图像和。经过图像配准，将2 幅SAR 图像进行共轭相乘可得干涉处理结果为

式中：为与相位无关的项。

从式（3）中可以观察到，目标径向速度与干涉相位的对应关系为

理想情况下，天线和具有相同的运动轨迹，因此对静止地面来说2 幅SAR 图像完全相同，经过干涉处理后静止目标的相位完全对消，仅运动目标具有与其径向速度对应的干涉相位，这就是利用SAR 顺轨干涉相位对动目标进行测速的原理。

2 时变基线倾角对干涉相位的影响

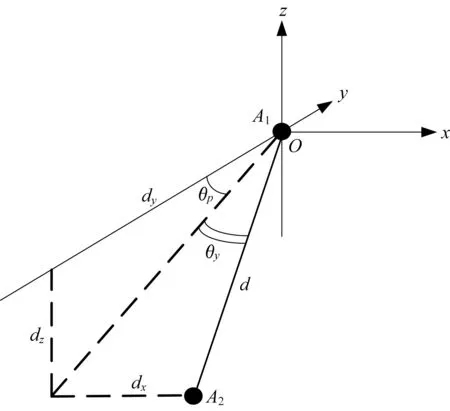
图2 基线倾角Fig.2 Schematic diagram of baseline inclination

图2 中：θ为俯仰角；θ为偏航角。由几何关系可得

在基线存在误差的情况下，对于径向速度为零的目标，此时天线相位中心到目标的瞬时斜距为

进行SAR 成像处理和图像配准后，2 幅SAR 图像进行共轭相乘可得

式中：为与相位无关的项。

由式（8）可以看出，由于基线倾角变化导致的交轨基线分量，两天线与地面静止目标的斜距历程不再相同，静止目标干涉相位可能不为零，产生了在方位向时变的平地相位。将导致对运动目标速度的错误估计，甚至无法检测到运动目标，因此必须采取措施去除平地相位的影响。

3 时变平地相位去除方法

对于平地相位的去除有多种处理方法。文献［17］在交轨干涉SAR 基线定标的基础上提出了通过布设地面控制点，并使用敏感度方程对机载ATISAR 基线误差进行定标，从而消除其影响的方法。但是由于基线会随方位时变，需要在测绘带内多处布设地面控制点，导致布设难度和成本上升，且某些地形可能难以布设，因此此方法在实际应用中收到限制。文献［18］基于较短时间内飞行平台俯仰角相对不变的假设，分两步依次校正平地和地形起伏引起的相位的盲校正方法。文献［19］提出一种采用分块处理和迭代运算的相位校正方法，通过在方位向和距离向分块并使用子块内相位均值多次迭代的方式，校正顺轨干涉相位中的时变交轨分量。以上基于干涉相位的时变平地相位校正方法由于分块和迭代的操作，分块大小需要根据情况调整，且处理效率上存在一定问题。针对这一问题，本文提出一种新的ATI-SAR时变平地相位去除方法。其原理和处理步骤如下：由式（8）可以看出，平地相位随方位时间、地距和斜距变化如下：

若在一定距离变化范围内，可以将地距视为近似不变，从而有

式中：()被定义为一个只与方位时间有关的因子。这在地形起伏不存在剧烈变化的情况下是合理的。

由式（10）可知，可以将同一方位时间一定距离范围内的平地相位视为只随斜距变化，因此可以对解缠绕后的干涉相位在距离向加窗截断，然后采用最小二乘法拟合得到平地相位的估计值。

基于以上假设，采用如下步骤进行平地相位去除，流程如图3 所示。

图3 平地相位去除方法流程Fig.3 Flow chart of the flat earth phase removal method

对原干涉相位进行相位解缠，得到无跳变的绝对相位。此步骤中，若相位变化较快导致直接解缠存在问题，可以先去除一假设的理想平地相位再进行相位解缠，通过迭代方式逐步逼近。

保证样本数量足够和地距近似不变的假设成立的条件下合理选取距离窗长，在解缠后干涉相位距离向滑窗截取数据。

对于每个方位时刻，利用距离窗内干涉相位，使用最小二乘法估计距离窗中心的因子()。

利用得到的因子()与距离窗中心对应的斜距反演平地相位Δ。

从原干涉相位中去除估计得到的平地相位。

4 仿真试验及结果分析

4.1 仿真结果

表1 仿真参数Tab.1 Simulation parameters

俯仰角和偏航角变化曲线如图4 所示，随方位时间的变化，俯仰角和偏航角在0°附近有微小变化。

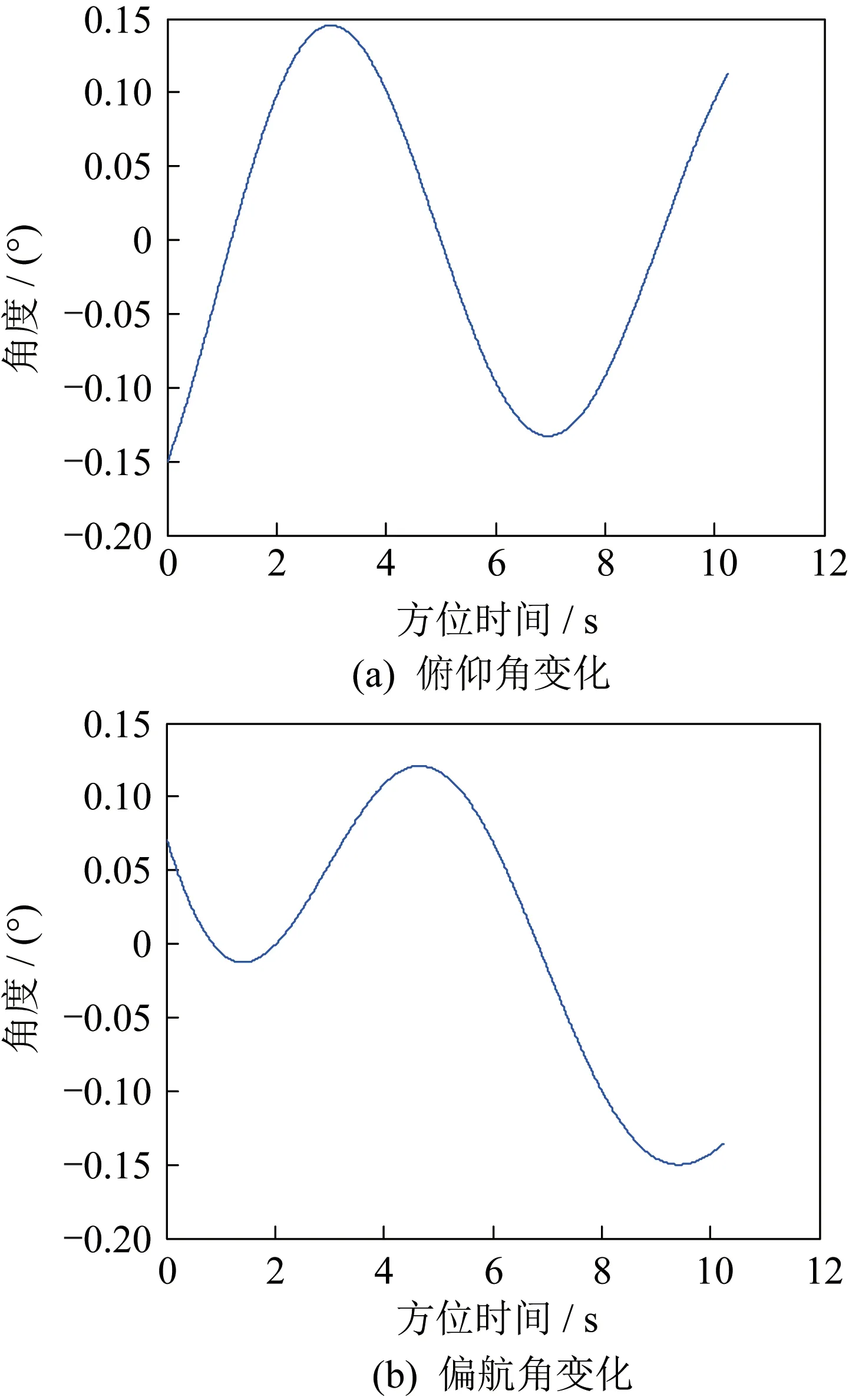
图4 俯仰角、偏航角变化Fig.4 Change curves of the pitch angle and yaw angle

仿真得到的干涉相位如图5 所示。图中可见，在这组仿真参数条件下，即使较小的俯仰角和偏航角误差也会引入较大的平地相位，场景中心处平地相位引起的相位误差达到约-2 rad，严重影响运动目标的速度反演。同时可以观察到由于场景较小，平地相位在距离向的变化较缓慢；而在方位向由于基线倾角变化导致的平地相位变化比较快，呈现与方位向平行的彩色条纹，并且由于相位缠绕的原因出现了相位跳变。

图5 干涉相位Fig.5 Interferometric phase

由上文讨论可知，所提方法是基于解缠后的绝对相位，因此首先需要对原干涉相位进行解缠。由于设置的基线倾角误差较小，时变基线倾角导致的平地相位变化条纹并不算密集，相位解缠过程相对来说比较容易，解缠后相位如图6 所示。

图6 解缠相位Fig.6 Unwrapped phase

选取距离窗长128 点，采用最小二乘法对解缠后相位进行参数估计，并进行平地相位反演，即可得到平地相位估计结果。从原干涉相位中减去估计的平地相位后得到的结果如图7 所示，可以看出随方位时间时变的平地相位已得到去除，设置的运动目标可以得到正确的检测和测速。

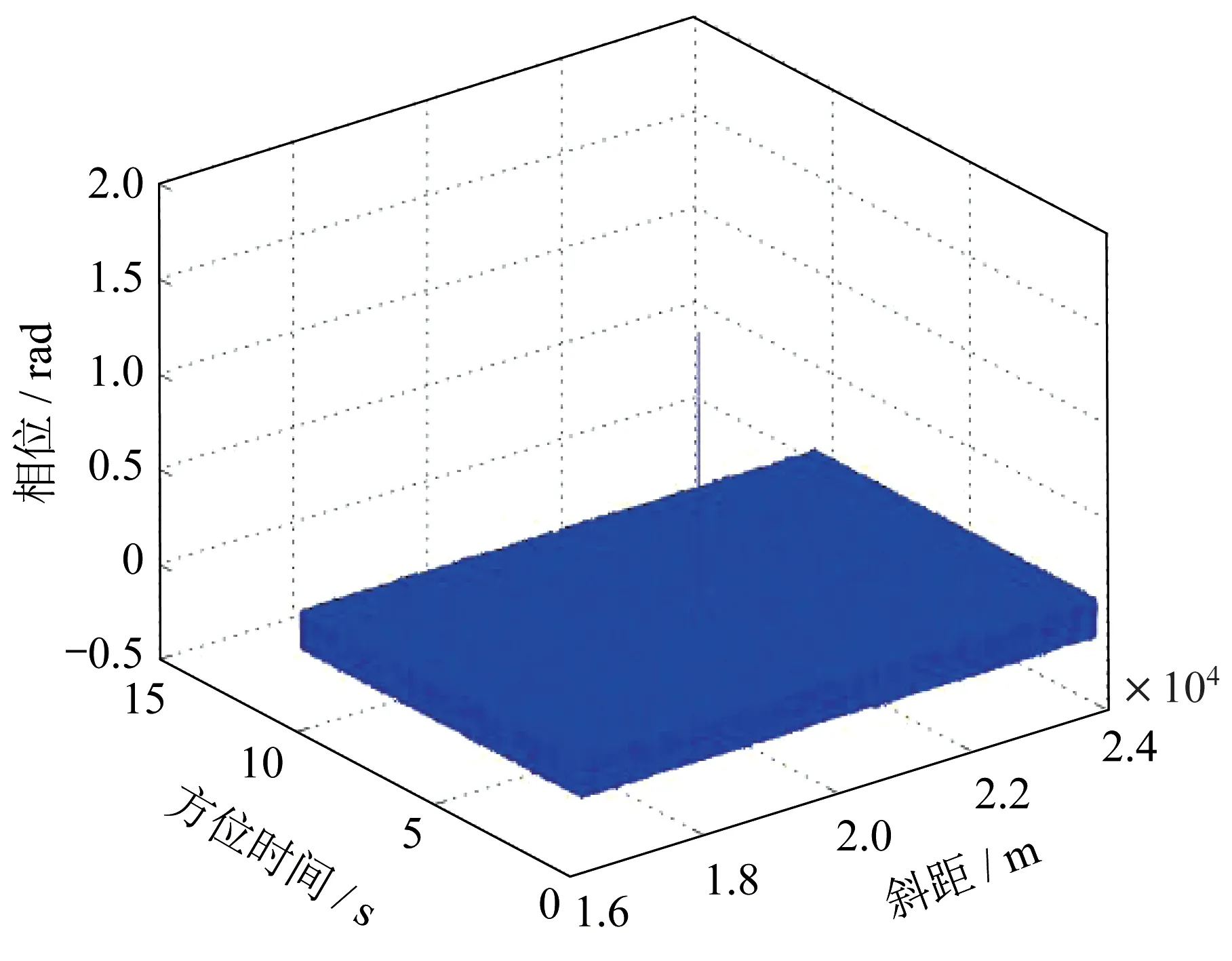
图7 动目标显示Fig.7 Ground moving target indication

4.2 结果分析

将通过本文方法得到的平地相位估计值与通过仿真参数得到的平地相位理论值相减，得到了平地相位反演误差，相对2π 相位归一化后的相位反演误差如图8 所示。图中可见，仿真中相对2π 相位归一化后的相位误差低于0.5%，说明本方法的平地相位估计精度较高，去除平地相位后可以满足对运动目标检测和测速的应用需求。

图8 平地相位反演误差Fig.8 Inversion error of the flat earth phase

同时对同一幅干涉相位图采用不同的窗长进行了平地相位反演仿真，并计算均方误差以分析窗长选择对性能的影响。平地相位反演的均方误差随距离窗长变化的关系图如图9 所示。图中可见，窗长较小和较大时平地相位反演误差将会快速上升，但总的来说选取窗长在1 000 点以内平地相位反演的误差都是较小的，计算出的相位均方误差在2×10以内。发生误差上升的原因在于窗长过小时，样本数太少导致最小二乘估计的误差较大；而窗长过大时，由于窗内距离变化较大，前一节提出的一定距离变化范围内将地距视为近似不变的假设不再成立，最小二乘估计得到的结果也将偏离真实值。因此为使误差尽可能小，窗长不能取太大也不能取太小，合理选择窗长可以得到更好的平地相位去除性能。

图9 相位反演均方误差Fig.9 Inversion mean square error of the flat earth phase

5 结束语

本文分析了ATI-SAR 在时变基线倾角影响下，其干涉相位中平地相位分量随方位时间、地距和斜距变化的关系。基于在一定距离变化范围内，可以将地距视为近似不变的假设下，提出一种基于回波数据的平地相位校正方法。该方法通过在解缠绕后的干涉相位的距离向进行滑窗，并使用最小二乘法估计和反演平地相位，从而将其去除。在理想平地假设的场景下，利用仿真数据对该方法进行了验证和误差分析，结果表明本文提出的方法具有较高的估计精度，去除时变平地相位后静止目标的干涉相位恢复到零附近，不再干扰对运动目标的检测和测速，且由于不存在分块和迭代的操作，此方法的处理效率较高。但是本文仅使用仿真的平地场景进行了验证，本方法在实测数据和复杂地形下的性能还有待进一步研究和改进。