基于GA－BP神经网络的轨道结构病害诊断方法研究

华 莉，孔尧尧，陈永逸，翟亚雷

（上海工程技术大学 城市轨道交通学院，上海 201620）

0 引 言

由于中国高铁高速发展，运营里程也随之增长。到2020年为止，中国铁路的运营总里程数达到14.6万公里，高铁运营里程数3.9万公里，占比高达26%，已成为世界上拥有最大铁路网和最完善高铁系统的国家，也随之改变了人们出行的习惯。据统计，中国高铁网已覆盖了约95%的百万人口地区。高铁运营里程和时间的增长，让轨道结构的可靠性、安全性、平顺性面临更高的挑战。由于复杂的地理环境和温度影响，以及考虑动载荷、内部应力等因素，轨道结构会出现各种病害。目前，国内外主要依靠人工目视检查和手动探伤来进行轨道结构检测，其效率低、风险大且漏检率高。随着人工智能、大数据和无线传感网络技术的发展，如何利用智能算法保证铁路运行的安全成为一项十分重要的研究课题。

新加坡学者Yang等利用塑料光纤传感器，对列车轨道结构中的疲劳裂纹进行实时监测，并进行故障诊断和跟踪其演变；李俊武等采取RS－BN算法，对轨道电路故障问题进行诊断。所以运用智能算法来保障铁路运行安全成为研究的热点。而随着智能计算机和故障诊断计算的不断发展，人工神经网络受到国内外专家和学者的关注。王英洁等提出了改进Elman神经网络故障诊断法，来应对变压器的伤损诊断问题；王力等面对模拟电路的故障诊断问题，提出了将神经网络运用于模拟电路上，并利用免疫遗传算法优化BP神经网络；燕宗伟等人为了提高管道检测准确率，提出了一种基于遗传算法优化的BP神经网络管道，用于检测泄漏的方法，有效提高了正确率。

本文提出一种基于BP神经网络的轨道结构病害诊断方法，BP神经网络算法在运算过程中会出现局部极限值，存在无法找到全局最小值的缺陷，导致训练的误差。相比而言，遗传算法的特点恰好可以弥补前者的缺点。因此，将遗传算法和BP神经网络结合起来可以达到更好的效果，将遗传算法运用在BP神经网络上对权值起到优化的效果，从而进一步提升BP神经网络效果。

1 BP神经网络

BP神经网络本质上属于多层前向型神经网络，这一技术在1986年被D.E Rumethart等人提出。该算法的根本是以正反向传播的方式，来寻求误差函数的最小值，由于误差函数具备负梯度方向这一特点，进而达到修改加权因子的目的，非线性理论中的最速梯度下降法往往在此处应用。算法通过储存大量输入与输出数据，并对输入和输出之间的映射关系进行表达，现已成为应用最广泛的人工神经网络系统。BP神经网络基本原理如图1所示。

图1 BP神经网络结构图Fig.1 Structure of BP neural network

由图1可知，信号的正向传播及误差的反向传播过程，是BP神经网络的基本运行模式。当信号从输入层进入后，将向前继续传播，直至到达隐含层；输入信号在隐含层经过不同的函数计算处理之后，会继续传播下去，最终到达输出层。当出现不同的输出和期望值时，则会转入误差反向传播这一过程中，途经隐含层并且向输出层逆向传递转移，再重新给每个单元传递不同的误差，便可对神经网络的权值进行修正。这一算法的训练过程就是通过正向传播和误差反向传播的往复循环进行，同时对权值也不断修正的过程。

2 遗传算法优化BP神经网络

2.1 遗传算法基本原理

遗传算法（Genetic Algorithm，GA）是一种典型的进化算法。基于达尔文进化论中的优胜劣汰原理和遗传机制，1975年，J.Holland教授提出了一种优化算法，很好的解决了传统寻优搜索算法（如：黄金分割法、最速梯度下降法、拉格朗日乘数法以及共轭梯度法等）在遇到复杂的非线性优化问题时，不能准确快速地寻求全局最优解这一科学瓶颈问题。同时，遗传算法还具有操作简单且全局搜索性能良好的特点，因而被广泛运用于机器学习和模式识别领域。遗传算法中优化问题的解对应于生物的染色体，这些解的集合叫做群体（）。通常来说，对于一个确定的优化问题，（）中的染色体个数被称为种群规模，其值是永恒不变的；适应度则是每个种群中各个元素对周遭环境的适应程度。GA算法是从可能存在最优解的区域中的某一种群开始，基于自然生存法则，选择适应度最大的个体进行遗传操作（如：组合、交叉、变异等操作），其它的个体将被淘汰，如此一步步迭代生成新的近似最优解，此次优化问题的全局最优近似解便是进行到最后一个种群中的最优个体。GA算法的流程如图2所示。

图2 GA算法流程图Fig.2 Flow chart of GA algorithm

2.2 GA优化BP神经网络

由于BP神经网络在整个网络训练过程中会存在局部极小值的问题，导致获得局部最优解的情况，而GA算法的全局搜索能力刚好弥补了BP神经网络的缺陷。两者结合既延续了各算法的优点，又弥补了各自的缺点，实现了故障诊断的高效、快速求解。GA_BP优化算法运用GA算法，将BP神经网络初始权值、阈值进行优化并对其编码，按照GA算法的运行步骤进行遗传进化，最后得到优化后的阈值、权值，将得到的数值重新投入BP神经网络模型中进行训练。GA_BP神经网络算法流程如图3所示。

图3 GA_BP神经网络算法流程Fig.3 GA_Flow chart of BP neural network algorithm

3 实验验证与分析

3.1 车轨耦合动力学模型

本文采用文献［13］中所提方法建立车辆－轨道耦合动力学模型，如图4所示。将四轴二系悬挂的客车模型作为车辆模型；在轨道模型中，以各个轨枕支点为基本单元，沿纵向进行离散化处理，每个支承基本单元为双质量、三层弹簧－阻尼模型；根据道床锥体受荷假设，可以把道床模拟成锥体。本文模型中的轨道长度l取120 m，轨枕间距l为0.6 m。文献［14］中指出，轨枕空吊、道床板结、扣件失效等轨下基础缺陷，属于动力型轨道刚度不平顺，若要对其进行模拟只需改变模型中所对应的刚度和阻尼即可。例如，轨枕完全空吊即完全失去工作能力可以设K＝C＝0；对于道床板结则相应的设K′＝η K、C′＝η C。 其中，η、η分别表示道床的刚度和阻尼变化系数。对于不同程度的病害，η、η可以在110之间取值。

图4 车辆－轨道垂向耦合模型Fig.4 Vehicle track vertical coupling model

通过改变轨枕下各支撑点的刚度和阻尼进行工况仿真，设置车辆行驶速度为200 km／h，选取轨道结构中心的51～150共100根轨枕进行研究，对不同程度轨枕空吊和道床板结工况下的轨枕振动进行了仿真，具体方案见表1。

表1 轨道结构在不同工况条件下的模拟Tab.1 Simulation of track structure under different working conditions

3.2 数据预处理

基于仿真可以获得轨枕振动的信号，对原始信号进行特征提取，提出基于VMD－MPE的病害特征提取方法。通过仿真得到轨枕4种服役状态的数据信号（见表1），经变分模态分解（Variational Mode Decomposition，VMD）后得到一系列IMF分量，计算各IMF分量的多尺度排列熵值（Multi－scale Permutation Entropy，MPE），实现对病害特征的提取。

以速度为200 km／h列车的1～20号轨枕为例，计算其经VMD分解后的值。其中，VMD算法分解个数5；算法中，嵌入维数5，时间序列长度4 096，延迟时间1，尺度因子12。在此参数情况下，不同工况的值见表2。（受篇幅所限，表中仅列出前十根轨枕数据）

表2 1～10号轨枕在列车速度200 km／h时不同工况下的MPE值Tab.2 MPE value of 1～10 sleeper under different working conditions at train speed of 200 km／h

3.3 轨道结构病害服役状态诊断

根据上述方法，以速度为200 km／h的列车为例，通过VMD－MPE算法对1～20号轨枕在正常、空吊、松散和板结4种工况下的振动信号进行处理后，计算各IMF的值，并构建高维特征向量组，作为BP神经网络模型的输入。通过计算得到一个12×400的向量组，选择前240组样本作为训练样本，80组样本为确认样本，80组样本作为测试样本。具体数据见表3。

表3 列车200 km／h速度下的实验数据描述Tab.3 Description of experimental data at train speed of 200 km／h

设最大训练步数为1 000步，训练目标最小误差为0.001，学习速率为0.01。训练结果如图5、6所示。

图5 误差分析图Fig.5 Error analysis diagram

由图5可以看出，BP网络训练第5代的结果最佳。训练样本、测试样本、确认样本的误差曲线呈现很好的相关性，最终达到了一个比较合适的误差值。观察图6得出，神经网络拟合度水平较高。其训练拟合度、测试拟合度和验证拟合度均达到95%以上，且总体准确率高达97.5%。

图6 回归分析图Fig.6 Regression Analysis

为了进一步验证本文所提VMD－MPE与BP神经网络结合方法的有效性，对不同速度下的列车进行仿真验证，其结果见表4。

表4 不同速度下列车的识别准确率Tab.4 Recognition accuracy of trains at different speeds

由表4结果可以看出，VMD－MPE和BP神经网络相结合的方法，在不同列车运行速度下，最高的识别准确率为99%，最低的识别准确率为93%，准确率有待提高。由于建立神经网络模型的过程中，权值和阈值直接影响网络模型的性能，造成训练时收敛过程极不稳定，从而影响模型的识别准确率。为了达到更加稳定的识别准确率，需要对模型的初始阈值和权值进行合理设置。因此，提出GA算法对模型进行进一步优化。经过多次仿真，验证了GA_BP神经网络方法对病害诊断的有效性。

以速度为200 km／h的列车为例，设置GA算法参数见表5。

表5 GA算法参数表Tab.5 Parameters of GA algorithm

经GA算法优化后，BP神经网络的最优阈值和初始值见表6。

表6 最优初始权值阈值Tab.6 Optimal initial weight threshold

将优化后的初始权值、阈值输入BP神经网络模型，训练100次后预测其输出，得到的BP训练误差和GA_BP训练误差如图7、图8所示。

图7 BP神经网络的训练误差Fig.7 Training error diagram of BP neural network

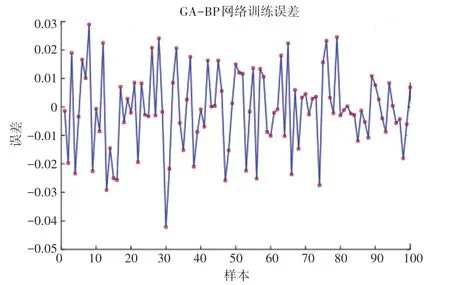
图8 GA_BP神经网络训练误差Fig.8 GA_BP neural network training error diagram

由图7、8可以看出，GA算法优化的BP网络识别更加精确，并且GA算法优化BP网络训练的误差平均值为0.001 12，而未优化的BP神经网络误差平均值为0.031 8，可见训练误差得到了很大的改善。此外，经GA算法优化后的BP神经网络识别准确率达到了99%，与优化前的93%相比，有了很大的提升。如图9、图10所示。

图9 BP神经网络识别准确率（93.8%）Fig.9 Recognition accuracy of BP neural network（93.8%）

图10 GA_BP神经网络识别准确率（98.9%）Fig.10 GA_Recognition accuracy of BP neural network（98.9%）

基于以上方法，对不同列车速度的轨枕振动信号进行识别，分别对优化前后的特征值进行训练和测试，最终诊断结果见表7。

表7 GA优化前后识别正确率对比Tab.7 Comparison of recognition accuracy before and after GA optimization

由表7可知，利用GA算法对BP神经网络进行优化后，轨道结构病害识别准确率均达到了98%以上，充分证明了基于GA算法优化BP神经网络的方法，在轨道结构病害识别及诊断上的有效性。

4 结束语

本文通过搭建车－轨耦合的动力学模型，仿真得到轨枕空吊、正常、道床松散和板结4种工况下轨枕的振动加速度信号。建立VMD－MPE算法对原始信号进行特征提取，通过BP神经网络对轨道病害进行识别诊断，并利用GA算法对BP神经网络的权值和阈值进行优化。对比优化前后识别结果发现，轨道结构病害识别准确率也有了明显的提高，均达到了98%以上，甚至可达到100%。充分证明了GA_BP神经网络的优化方法在轨道结构病害识别及诊断上的有效性，提高了诊断准确率。