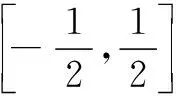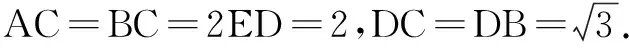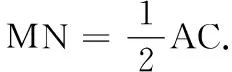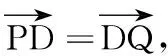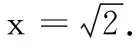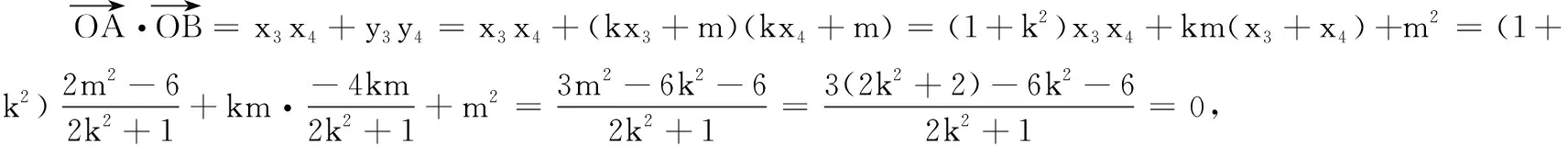高三数学综合测试
一、单项选择题(本大题共8小题,每小题5分,计40分)
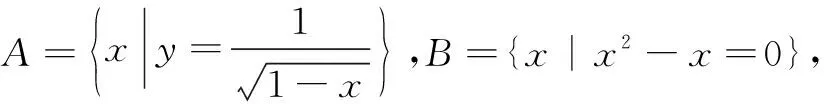
(A)∅ (B){0}
(C){1} (D){0,1}
2.已知a>0,则“aa>a3”是“a>3”的( )
(A)充分不必要条件
(B)必要不充分条件
(C)充要条件
(D)既不充分也不必要条件
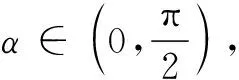
4.某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e=2.718… 为自然对数的底数,k,b为常数).若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是( )
(A)16小时 (B)20小时
(C)24小时 (D)28小时
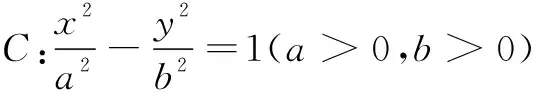
6.第十三届冬残奥会于2022年3月4日至3月13日在北京举行.现从4名男生,2名女生中选3人分别担任冬季两项、单板滑雪、轮椅冰壶志愿者,且至多有1名女生被选中,则不同的选择方案共有( )
(A)72种 (B)84种
(C)96种 (D)124种
7.若4x=5y=20,z=logxy,则x,y,z的大小关系为( )
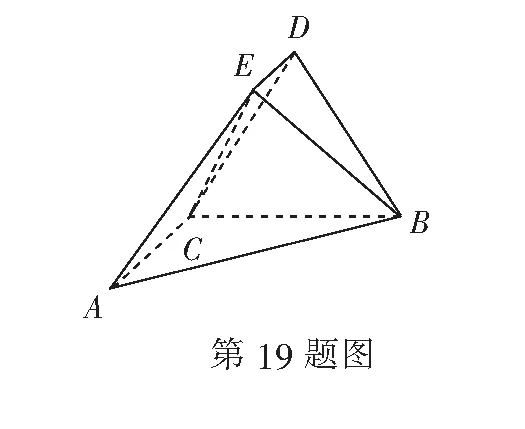
(A)x (C)y 二、多项选择题(本大题共4小题,每小题5分,计20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分) 9.已知函数f(x)=2sin x,下列结论正确的有( ) (A)f(x)是周期函数 (B)f(x)的图象关于原点对称 10.已知圆C:x2+y2-4y+3=0,一条光线从点P(2,1)射出经x轴反射,下列结论正确的是( ) (A)圆C关于x轴的对称圆的方程为x2+y2+4y+3=0 (B)若反射光线平分圆C的周长,则入射光线所在直线方程为3x-2y-4=0 (C)若反射光线与圆C相切于A,与x轴相交于点B,则|PB|+|BA|=2 11.如图,在直三棱柱ABC-A1B1C1中,AC=BC=1,AA1=2,D是棱AA1的中点,DC1⊥BD,点E在BB1上,且BB1=4BE,则下列结论正确的是( ) (A)直线DC1与BC所成角为90° (C)CE⊥平面BC1D (D)直三棱柱ABC-A1B1C1外接球的表面积为6π 12.某人投掷骰子5次,由于记录遗失,只有数据平均数为3和方差不超过1,则这5次点数中( ) (A)众数可为3 (B)中位数可为2 (C)极差可为2 (D)最大点数可为5 三、填空题(本大题共4小题,每小题5分,计20分) 13.在(1-x)4(2x+1)5的展开式中,含x2的项的系数是______. 15.以模型y=cekx(c>0)去拟合一组数据时,设z=lny,将其变换后得到线性回归方程z=2x-1,则c=______. 四、解答题(本大题共6小题,计70分.解答应写出必要的文字说明、证明过程或演算步骤) (1)求A; (1)证明:数列{bn+2}为等比数列,并求出{bn}的通项公式; (2)求数列{an}的前2n项和. (1)求证:平面ABE⊥平面ABC; (2)求二面角A-BE-C的余弦值. (1)求该选手参加比赛至少射中1次的概率; (2)求本次比赛选手平均射中多少次? (2)在圆O:x2+y2=2 上取一点M,过点M作圆O的切线l′与椭圆C交于A,B两点,求|MA||MB| 的值. 22.(本小题满分12分)已知函数f(x)=ln(x+1)-ax+1(a∈R). (1)当a>0时,设函数f(x)的最大值为h(a),证明:h(a)≥1; 参考答案 一、单项选择题 1.B;2.B;3.A;4.C;5.C; 6.C;7.D;8.D. 二、多项选择题 9. AD;10.ABD;11.ABD;12.AC. 三、填空题 四、解答题 所以bn=3·2n-1-2,n∈N*. (2)由(1)可知bn=3·2n-1-2,n∈N*,即a2n-1=3·2n-1-2,n∈N*. 又AC⊥平面BCD,AC⊂平面ABC,所以平面ABC⊥平面BCD. 因为DC=DB,所以DM⊥BC.又平面ABC∩ 平面BCD=BC,DM⊂平面BCD,所以DM⊥平面ABC. 所以EN⊥平面ABC,而EN⊂平面ABE,所以平面ABE⊥平面ABC. (2)由(1)可知AC⊥BC,EN∥DM,EN=DM,EN⊥平面ABC,平面ABE⊥平面ABC. (2)令该选手射中的次数为X,则X可能的取值有0,1,2,3. 综上,对圆O上任意一点M处的切线交椭圆C于点A,B,都有OA⊥OB. 在Rt∆OAB中,由∆OAM与∆BOM相似,得|MA||MB|=|OM|2=2. 22.(1)f(x)的定义域为(-1,+∞). 当-1 所以g(x1)+g(x2)<2. ·告读者·应广大读者要求,自2011年起,本刊初、高中版分别增加“教研版”,《初中数学教与学》(教研版)邮发代号为28-424,《高中数学教与学》(教研版)邮发代号为28-425.欢迎各地中学数学教师、数学教育工作者,以及数学爱好者到当地邮局订阅.如若错过时间,可与编辑部联系邮购. ·告作者·为适应我国基础教育信息化建设,扩大本刊及作者知识信息交流渠道,本刊已被“中国基础教育知识仓库(CFED)”、“中国知网(CNKI)”等收录.如作者不同意文章被收录,请在来稿时向本刊声明.