带限位双层隔离系统冲击响应计算方法研究
贾国辉, 孙自强, 张 磊, 闫 明
(1.沈阳工业大学 机械工程学院,沈阳 110870;2.海军研究院,北京 100161)
为避免重要舰船设备遭到破坏,设计时大多采用为设备安装隔振器的方法[1],通常隔离系统的固有频率较低,因而在遭受冲击载荷时加速度响应幅值较小,但却产生了很大的相对位移,有可能超过设备外接管系的承受极限,甚至超过隔振器本身的极限变形能力。为了防止设备的位移超过允许范围,在设备上安装限位器是行之有效的方法之一[2-3],限位器安装时通常留有一定的间隙,这使得带限位系统存在二次冲击问题。
安装有弹性限位器的系统具有刚度分段线性的特点,国内外学者对分段线性系统的动态响应计算进行了广泛的研究。其中包括以摄动法、平均法、谐波平衡法和增量谐波平衡法等为代表的近似解析法[4~6],但这些方法应用范围仅限于弱非线性系统,对于具有强非线性特点的分段线性系统很难给出准确解。对于多自由度的强非线性系统,通常只能采用数值方法求解[7-8],但这些算法通常需要反复迭代计算,使计算效率非常低,特别是收敛精度设置得很高时。最后一种是接合法,首先分段求解线性方程,然后利用分段点上的运动连续性条件进行接合[9-10]。文献[11]建立了含间隙弹性机械关节的数学模型,导出了运动的动力学方程。文献[12]研究具有分段线性-非线性刚度项的单自由度系统的共振和稳定性,采用修正摄动法求解了弱非线性方程的近似解。文献[13]用分段延拓法对二自由度碰撞振动系统进行了研究。由接合法建立的线性方程通常左侧含有带间隙项,这使得建立的线性方程无法通过模态叠加法、直接积分法、动力设计分析方法等进行求解。
本文在接合法的基础上进行改进,提出分段建立标准形式方程的方法。以两自由度分段线性系统为研究对象,首先采用坐标平移的方法分段建立标准形式线性方程,然后使用模态叠加法求得了每段的冲击响应解析解,最后用MATLAB编写了求解程序,进而分析了限位器参数对冲击响应的影响。
1 坐标平移方法
图1示出了单层带限位隔离系统简化后的物理模型,图中m表示被隔离设备的质量,k1表示隔振器的刚度,k2表示限位器的刚度,Δ表示限位器单侧间隙值,x(t)表示设备的位移随时间t的响应函数,u(t)表示系统受到的冲击激励函数。
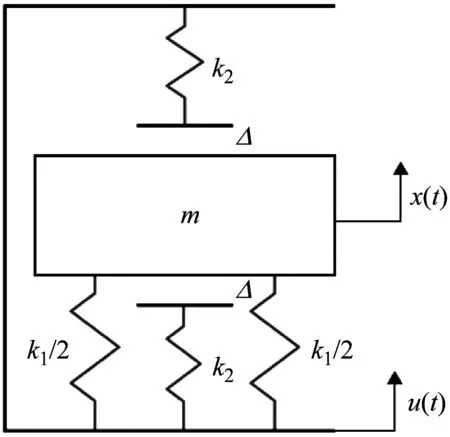
图1 单层带限位隔离系统Fig.1 Shock isolation system with double displacement restrictors
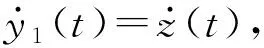
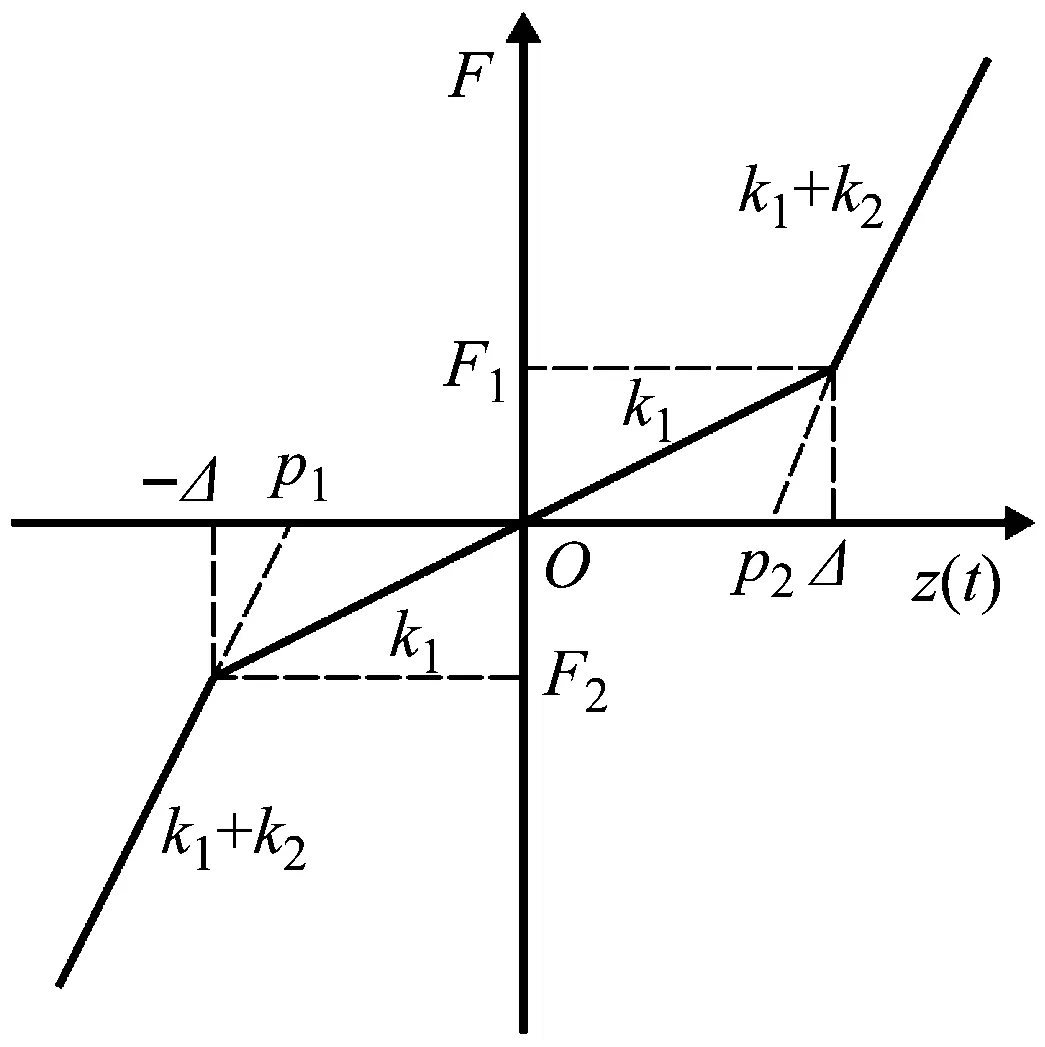
图2 力-位移关系曲线Fig.2 Force-displacement curve
2 双层带限位隔离系统数学模型
图3示出了双层带限位隔离系统简化后的物理模型,图中m1和m2分别表示基座和被隔离设备的质量,k1表示基座的刚度,k2表示隔离器的刚度,k3表示限位器的刚度,Δ表示限位器单侧间隙值,x1(t)表示基座的位移随时间t的响应函数,x2(t)表示设备的位移随时间t的响应函数,u(t)表示系统受到的冲击激励函数。
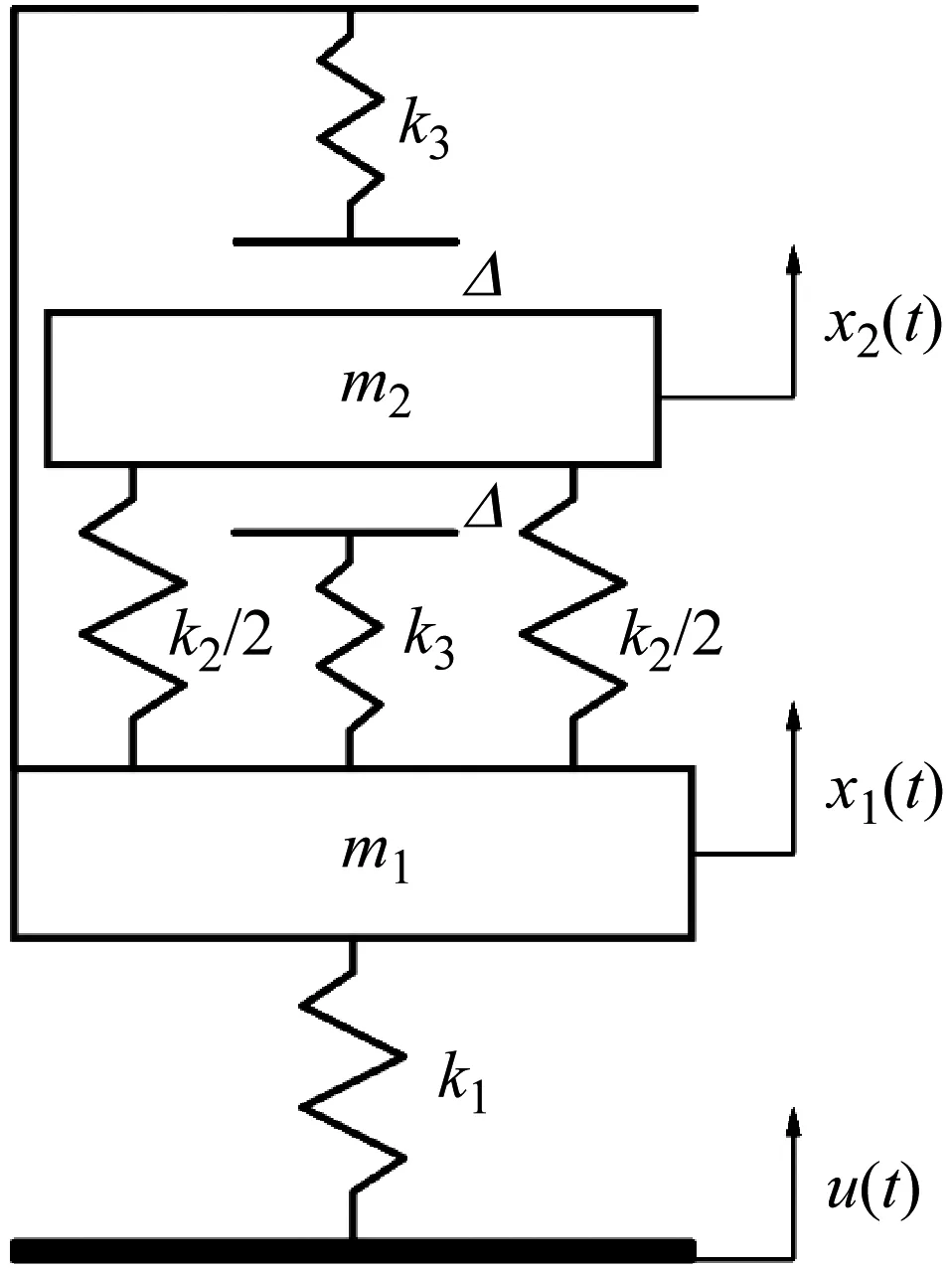
图3 双层带限位隔离系统Fig.3 Double-deck shock isolation system with double displacement restrictors
令基座相对固定基础的位移z1(t)=x1(t)-u(t),设备相对固定基础的位移z2(t)=x2(t)-u(t),设备相对于基座的位移z(t)=z2(t)-z1(t),为方便分析,令进入状态(Ⅰ)、(Ⅱ)和(Ⅲ)的广义时间分别为t0、t1和t2。当系统受到冲击激励作用时,可以得到运动微分方程:
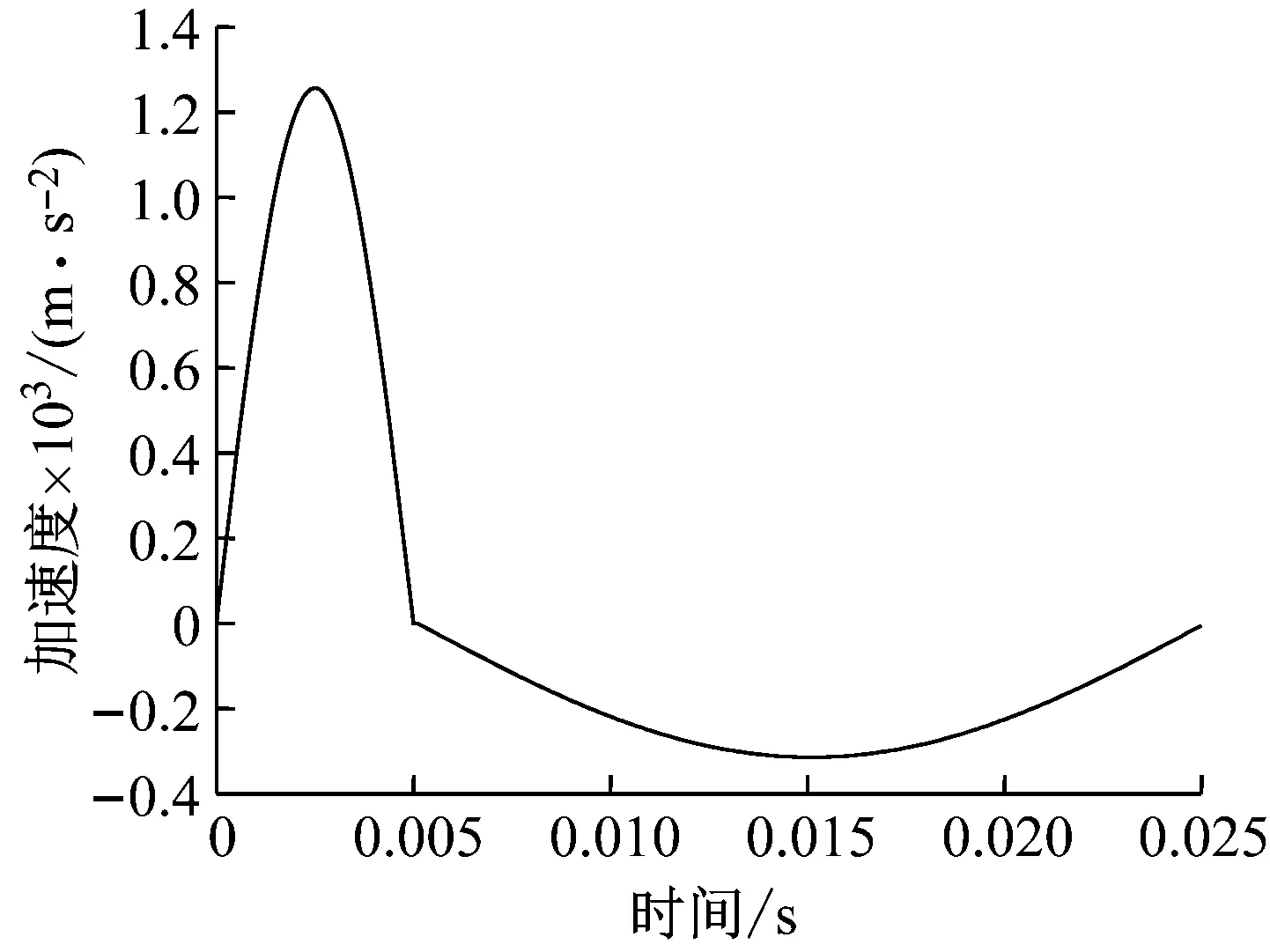
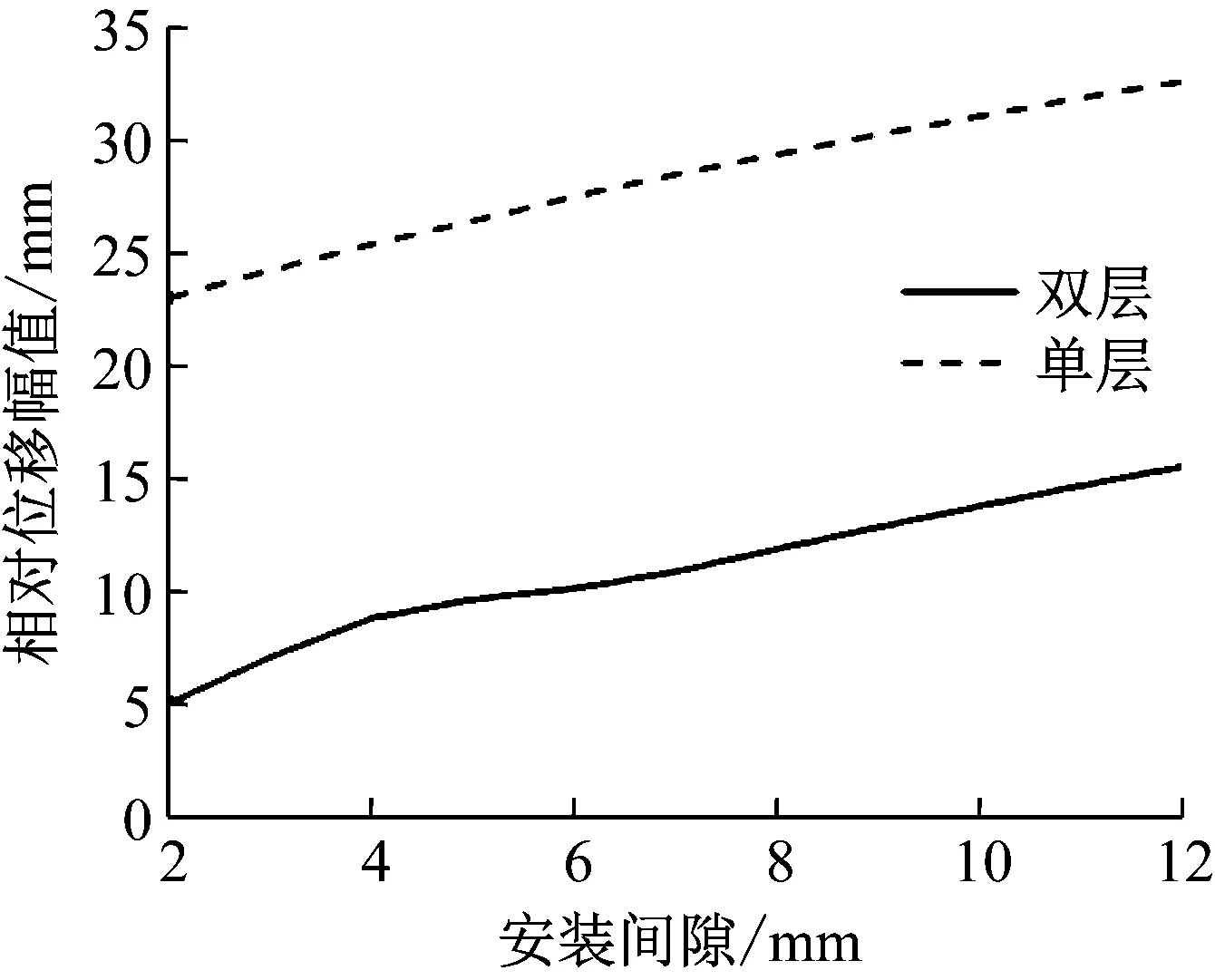
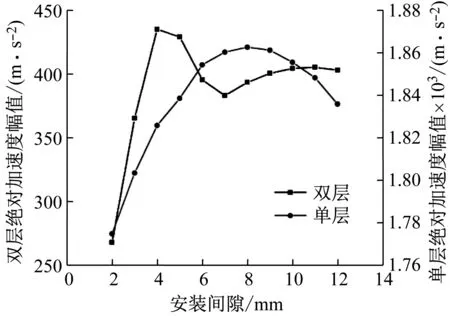
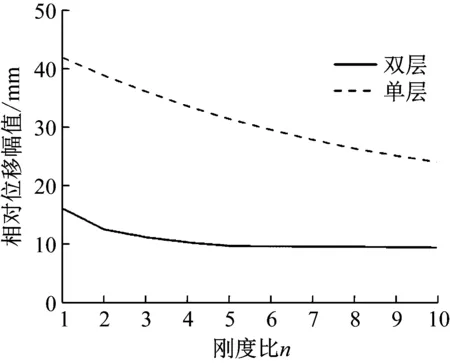
(Ⅰ) 未接触限位器状态(-Δ (1) 写成矩阵形式为 (2) 首先讨论特征值问题,设式(2)解的形式为z(t)=Aeiωt,可得 (3) 对应的系统频率方程为 (4) 解得系统的两阶固有频率为 (5) 式中:ω01=(k1/m1)1/2为基座单独存在时的固有频率,ω02=(k2/m2)1/2为隔振系统的固有频率;ω1和ω2分别为双自由度系统的一、二阶固有频率。为求出模态向量,将式(5)代入式(3)第二式,并取A2=1,得到坐标变换矩阵为 (6) 进行如下坐标变换 (7) 式中,q(t)为自然坐标。将式(7)代入式(2),并在方程两边左乘[U1]T得到解耦方程组的矩阵形式为 (8) 式中, 对解耦后的系统利用杜哈梅积分求得 通过坐标变换式(7)可得 (11) z2(t)=q1(t)+q2(t) (12) 设备相对基座的位移为 (13) 根据式(1)第二式,设备的绝对加速度响应为 (14) (Ⅱ) 设备接触到下限位器状态(z(t)<-Δ) 设备接触下限位器后,经过坐标平移,新的坐标为 (15) 同理,对接触后的两自由度系统解耦可得 (16) 式中:ω11、ω22为接触限位器后两自由度系统的一、二阶固有频率;ω03=[(k2+k3)/m2]1/2为限位器和隔离器同时作用时系统的固有频率。 新两自由度系统的坐标变换矩阵为 (17) 式(8)中的参数变为 (18) 通过坐标变换,确定解耦后的初值为 (19) 对解耦后的系统利用杜哈梅积分求得 原坐标系下设备的相对位移响应为 (22) 设备的绝对加速度响应为 (23) (Ⅲ) 设备接触到上限位器状态(z(t)>Δ) 同理,设备的相对位移响应为 (24) 设备的绝对加速度响应为 (25) 某双层隔离系统,设备质量m2=1 200 kg,基座质量m1=1 074.7 kg,上层隔振器总刚度k2=1.12×107N/m,下层隔振器总刚度k1=7.2×106N/m。将以此为基础,对限位参数进行设计。 根据联邦德国国防军舰艇建造规范BV043/85的规定,采用正负双半正弦波作为冲击载荷输入,冲击载荷如图4所示。图4中,正波幅值1 256.637 1 m/s2,脉宽0.005 s,负波幅值314.159 3 m/s2,脉宽0.02 s。 图4 冲击载荷Fig.4 Shock load 根据上述确定的隔离系统参数和冲击载荷,令限位器刚度与隔振器刚度的比值n=k3/k2为8。分别计算不同安装间隙Δ(2~12 mm)下单层和双层隔离系统的冲击响应,分析限位器安装间隙对冲击响应的影响。相对位移幅值随安装间隙的变化如图5所示。由图可见,相对位移幅值随安装间隙的增大近似线性增大;双层系统的相对位移幅值略大于安装间隙,而单层系统要远大于安装间隙,其主要原因是双层系统中能量能够传递给基座,而单层系统中的能量几乎都用来克服限位产生位移。 图5 相对位移幅值随安装间隙的变化曲线Fig.5 Relative displacement vs. installation clearance 图6示出了绝对加速度幅值随安装间隙的变化。由图可见,单层系统中加速度先增大后减小,呈现倒“V”型,这样就存在某一特殊间隙使加速度取到了极大值,而在双层系统中,加速度先增大后减小,再增大后减小,呈现“M”型,这样就存在某两个特殊间隙使加速度取到极大值。 图6 绝对加速度幅值随安装间隙的变化曲线Fig.6 Absolute acceleration vs. installation clearance 当限位器安装间隙很小时或趋近于零,基座位移达到最大,基座加速度较小,系统相当于上层定刚度的双层隔离系统。可见设备的相对位移和加速度响应的降低可能以牺牲基座的相对位移为代价。 隔离系统参数和冲击载荷不变,令限位器单侧安装间隙Δ为5 mm。分别计算不同刚度比n下单层和双层隔离系统的冲击响应,分析限位器刚度对冲击响应的影响。相对位移幅值随刚度比n的变化如图7所示。由图可见,单层系统中位移随着刚度比n的增大近似线性减小,而在双层系统中,在达到某一足够大的刚度比之前位移快速减小,继续增大刚度比位移近似水平,而加速度在这一刚度后增大速度加快。绝对加速度幅值随刚度比n的变化如图8所示。由图可见,随着刚度比n的增大,加速度总体上都呈现上升的趋势。限位器刚度的增大总体上会导致基座位移和加速度的增大,其原因是克服限位过程中能量向基座传递。 图7 相对位移幅值随刚度比n的变化曲线Fig.7 Relative displacement vs. stiffness ratio n 图8 绝对加速度幅值随刚度比n的变化曲线Fig.8 Absolute acceleration vs. stiffness ratio n 同时不难发现,在刚度比小于1.9单层限位器随着刚度比的增加相对位移减小的同时,加速度则快速上升;而对于双层限位器加速度上升的则缓慢的多。通过计算可知,刚度比为1.9时相较于刚度比为1时,相对位移下降了25%,而加速度只增加了3.5%;单层则是相对位移下降了10%,加速度增加了22.3%。从中不难发现双层限位器存在一个较优间隙,能够快速减小被保护设备的缓冲位移距离,同时不会很大增加由于限位放大的加速度。 为了验证模型的正确性,设计试验装置如图9所示。其中,1代表限位器,2代表设备质量,3和5为由双压缩弹簧结构组成的隔离器,4代表由各部分组成的基座质量,设置限位器单侧安装间隙Δ=5 mm,限位器刚度与上层隔离器刚度比为8。在跌落式冲击试验机上进行试验,由台面采集到的冲击信号为峰值24g,脉宽7.5 ms半正弦脉冲。 图9 试验装置Fig.9 Test device 相对位移响应曲线和加速度响应曲线如图10和图11所示。由图可见,试验结果和仿真结果具有较高的一致性,峰值误差在20%以内。由于阻尼的作用,试验中的相对位移和加速度不断衰减,试验结果峰值略小于仿真结果峰值。说明按此法获得的仿真峰值留有一定的安全系数。 图10 设备位移响应曲线Fig.10 Relative displacement of equipment 图11 设备加速度响应曲线Fig.11 Absolute acceleration of equipment (1) 提出的坐标平移法简化了建立线性方程的过程,得到的线性方程左侧具有标准形式,可以配合模态叠加法使用,提高了计算效率。坐标平移的方法,以每段线性与横轴的交点,即虚拟平衡点作为新的坐标原点建立坐标系,如此建立的线性方程左侧具有标准形式,能够采用常规的线性方法进行求解。接合法得到的是精确解,相较于数值方法具有更高的精度。设计了带限位器双层隔离系统试验装置,试验与仿真结果比较吻合,验证了模型的正确性。 (2) 单层系统中存在一个特殊安装间隙使加速度取到极大值,双层系统中这样的间隙有两个,应用本文提供的方法可以计算出此间隙值,此特殊间隙随冲击载荷变化。在双层系统限位器设计时,在保证设备振动性能的前提下应该尽量减小间隙,在第一个特殊间隙前选取间隙值,当小间隙不满足要求时,应该在两间隙间进行选取,以此类推。 (3) 双层系统中,随着限位器刚度的增大,相对位移幅值迅速减小,原因是能量不断的向基座转移,在达到一足够大的刚度后位移几乎不发生变化,稳定在略大于安装间隙的位置,继续增大刚度导致加速度增大速度加快,因此每个安装间隙存在与之对应的最大理想刚度使其性能达到最大化。3 冲击响应计算与分析
3.1 限位器安装间隙对系统冲击响应的影响分析
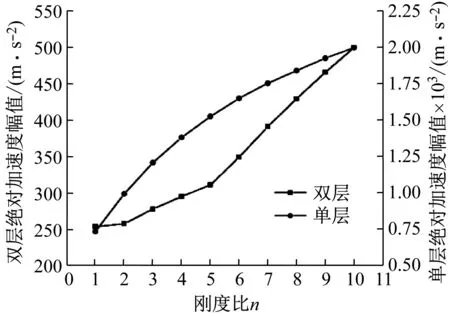
3.2 限位器刚度对系统冲击响应的影响分析
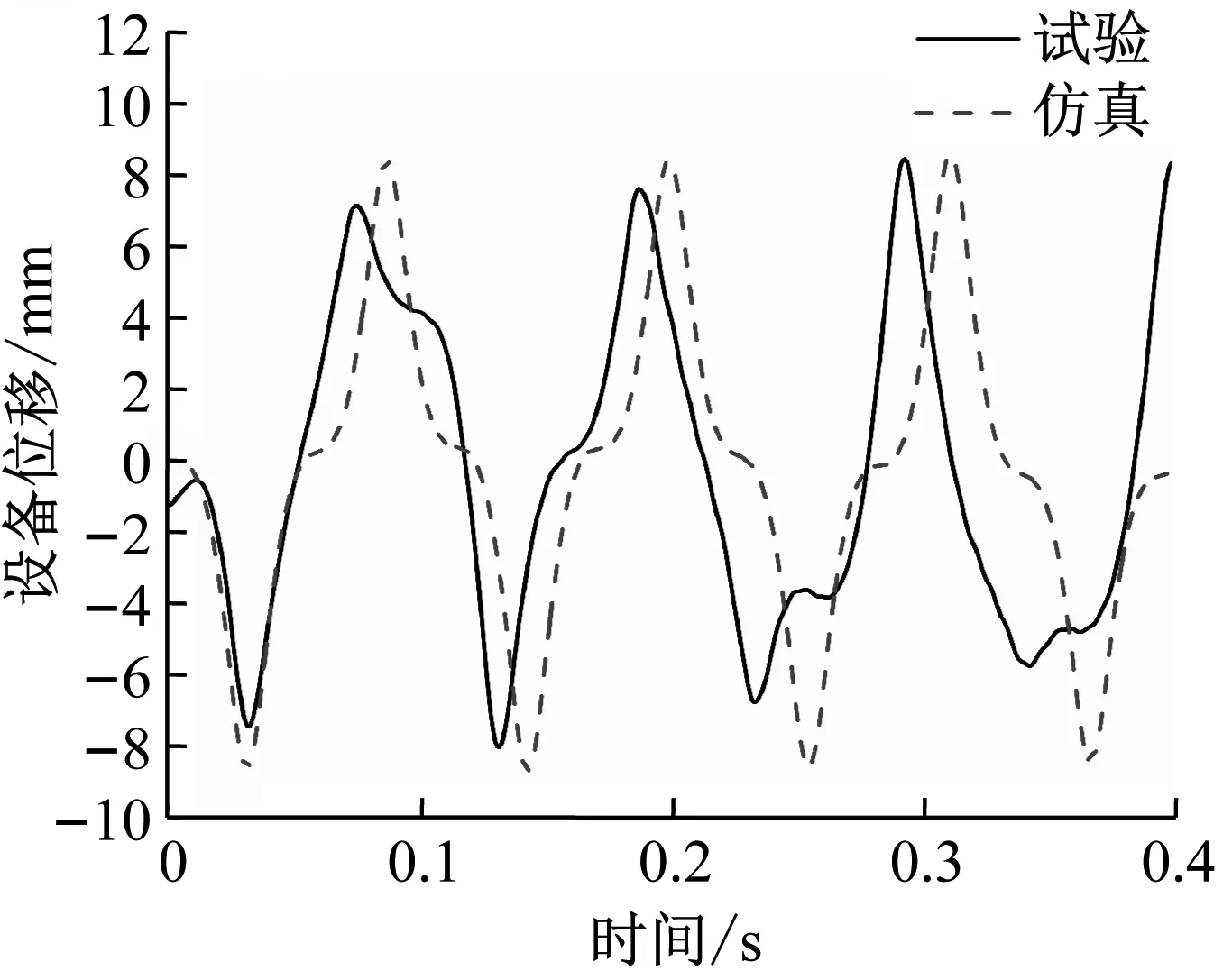
3.3 冲击试验与仿真结果对比


4 结 论

