聚焦核心素养,凸显过程方法——以一道几何综合题为例

广东省广州市第一一三中学(510630) 余雪娇

1 试题呈现(广州中考第24题)

如图1,等边ΔABC中,AB=6,点D在BC上,BD=4.点E为边AC上一动点(不与点C重合),ΔCDE关于DE的轴对称图形为ΔFDE.

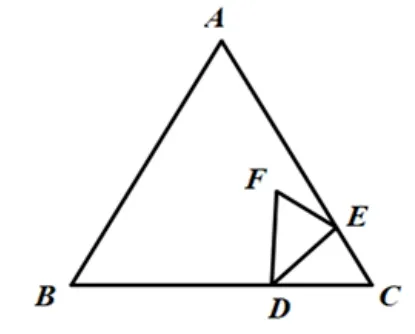
图1

(1)当点F在AC上时,求证:DF//AB;

(2)设ΔACD的面积为S1,ΔABF的面积为S2,记S=S1−S2,S是否存在最大值?若存在,求出S的最大值;若不存在,请说明理由;

(3)当B,F,E三点共线时,求AE的长.

2 核心素养视角下的特色解读

2.1 层次分明,关注个体

本题图形简洁,等边三角形加轴对称,亲和力强.问题设置3小问,起点低,入口宽,使不同层次学生展示不同的思维水平.第1问:直接利用“同位角相等”即可判断两直线平行,大部分学生可解.第2问:从条件DF=2发现隐形圆.把问题转化成圆外点与圆上动点距离最值问题.思维含量大,能真正考察出学生分析问题,解决问题的能力.第3问:求线段长度,熟而不俗.考察构图、设元;勾股定理、等面积法、相似等核心知识.综合性强,计算量大,能考察优秀学生综合素养.三个小问由基础知识到核心知识、数学思想方法,再到思维内化迁移,拾级而上,层层推进,梯度明显,有很好的区分度.体现数学课程应致力于实现义务教育阶段的培养目标,要面向全体学生,适应学生个性发展的需要,使得人人都能获得良好的数学教育,不同的人在数学上得到不同的发展.

2.2 解法多样,凸显通法

本题第(3)小问,目标明确:求线段AE的长.但解法多样(据笔者所知,有7种解法)彰显不同的思维层次.考察学生运用知识的灵活度和综合能力;考察学生的几何构图能力和计算能力.

图2

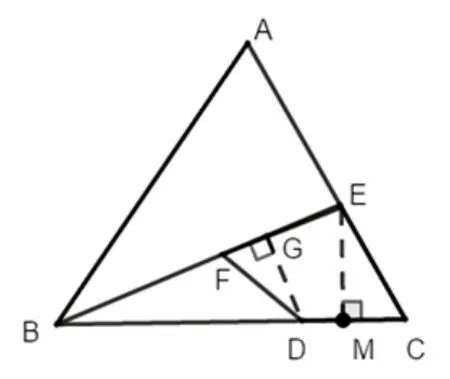
图3

解法7以点B为坐标原点,BC所在的直线为x轴建立平面直角坐标系.求直线BE、AC的交点E坐标,再把坐标转化为线段.

众多的解法,均体现求线段的二大基本思路.思路一:几何角度(用勾股、相似、面积法等求相关线段)思路二:函数角度(函数图像交点坐标向线段转化).其中解法6,7是高中阶段的方法.正弦、余弦定理是高中解三角形的基本方法;建系在理论上可以解决所有的解析几何问题,但运算量超大.所以高中的两种方法并没有优势,体现中考的公平性.其余的解法都围绕60°构造直角三角形,通过设元,用勾股定理、相似、等面积法、三角函数为桥梁,建立方程求解.突出初中阶段求线段的通性通法.关注数学内涵,压轴题回归数学本质,体现通性通法,力求考查学生数学思维的逻辑性、深刻性、慎密性.

3 教学导向分析

3.1 培养几何直观,提高解题能力

几何直观是初中生解决几何问题的必备能力.现在的课堂,盛行学案卷,图形已经呈现,学生无需画图.这削弱了学生画图能力以及对图形整体把握的能力,无法快速捕捉隐含图形中有价值信息.笔者认为几何的教学中,首先让学生有画图意识,培养画图习惯.对静态题,在学卷不设置图,要求学生根据题目正确画出图形,训练文字语言向图形语言转换能力;或者图形中留空,让学生根据条件补全图形.对几何的动态题,引导学生在关键的位置或特殊位置画出符合题意的图,借助图形直观观察分析归纳变中不变量,寻求突破.更多的关注画图探究过程,创设实验或操作的机会,让学生通过感官直接获取解题经验.其次,课堂中注重图形的组合与分拆的渗透.如全等三角形的学习,可以让学生依托两个全等的直角三角形.通过平移、轴对称、旋转进行组合,形成一些基本图形;再适当添加线条,形成复杂图形;最后在复杂图形背景下抽离基本图形,再分拆成独立的两个三角形.通过图形的重组分拆,培养图感.在繁与简的变换过程,领悟图形语言,提升几何直观想象,在图形的生长过程中,自然炼就学生对图形整体把控力、驾驭力.

3.2 夯实通性通法,内化数学思维

一题多解可以激发学生学习的兴趣,开拓思路.但课堂上,并不是为方法的展示而展示.教师应当培养学生解题反思习惯,优化解法.特别要“多法归一”或“多题归一”.哪些是针对某条件的技巧性解法;哪些是有共性,可以迁移的.适用解决普遍问题的方法要提炼;着重研究、剖析、形成解题策略.淡化技巧,重视通性通法的教学.因为通性通法往往承载着核心知识或者基本技能.对于通性通法的教学,可以采用“以退为进”模式.数学家华罗庚所言:善于退,足够的退,退到最原始而不失重要性的地方.例如:割补法是解决直角坐标系下图形面积问题的通法.为了让学生更好的掌握割补法,可以先退为特殊的三角形——直角三角形,再变斜三角形,最终为任意放置的斜三角形(如图4).在简单图形中,彻底掌握割补法,领悟化斜为直的思想.然后通过加线条或图形、背景的变化;增加条件或弱化条件等,把“先行组织”改得“面目全非”,训练学生对方法的迁移能力,这为进.通过退—进,学生达到基本技能娴熟.化陌生为熟悉问题,提高在新情境下解决问题的能力.学生在题目表征变化中领悟不变的数学方法与思想,利于思维的灵活性,内化数学思维.

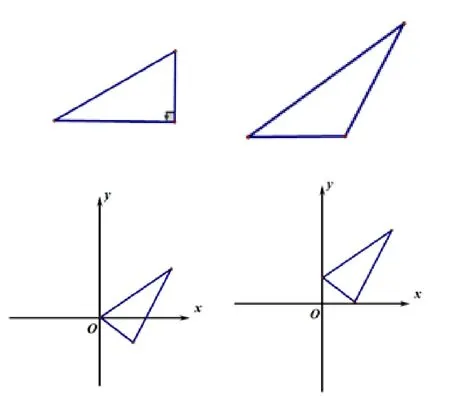
图4

3.3 重概念轻模型,回归数学本质

李邦河院士说,数学根本上玩概念,不是玩技巧,技巧不足道也.目前,很多老师不重视概念教学.“一个定义,三项注意”,以习题形式代替概念的探索.学生停留在机械的记忆层面,没有彻底的理解概念本质.本题的第(2)小问,若学生有经历圆概念的形成,就明白圆的本质:到定点距离等于定长的点的集合,隐形圆就跃然纸上.教学过程中,概念教学不应该走过场.要借助具体实例,从数学概念体系发展过程或解决实际问题的需要引入概念,体现学习的意义.提供典型丰富的实例,让学生展开观察、分析各事例的属性;比较、综合、归纳共同特征,形成概念.要学生经历概念的形成,设计基本的活动经验,包括概念的辨析,更好地理解概念的内涵与外延,直抵本质.同样,一些基本模型,不应该停留在记忆套用的层面.应该有系列活动,让学生发现模型,回归模型的本质,让学生明白模型蕴含的知识内在关联.例如:共斜边直角三角形(图5,图6)、旋转会产生圆(图7).这模型本质上是圆定义:到定点距离等于定长.一道高水平的题目,思维含量极高,无法简单的去套,而是学会分析,转化,最终回归到数学本质.

图5

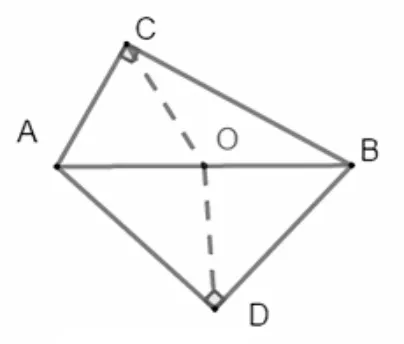
图6

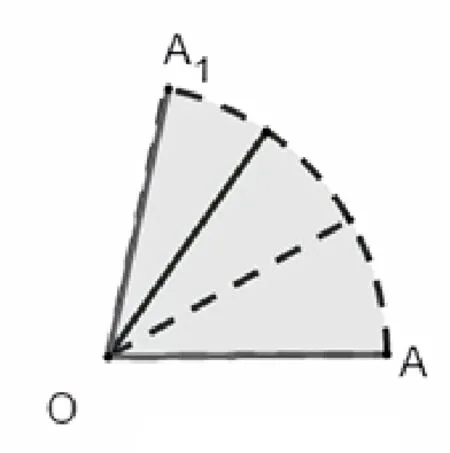
图7

4 结束语

《义务教育数学课程标准》提出:学生学习要获得适应社会生活和进一步发展所必要的数学的基础知识、基本技能、基本思想、基本活动经验.因此,教学过程中应回归教材,注重概念教学;抓住数学本质,关注学生学习过程.让学生充分经历知识形成的过程,促进学生对知识的深度理解.在真正的数学活动中积累学习和解题经验,发展数学核心素养.解题教学中关注解题通性通法的研究;渗透数学思想,训练学生寻找解题切入点的技能,提升思维品质,提高解题能力.