基于多孔介质模型的非织造布阻力特性研究
胡汝生,刘 寅,杜晨阳,王仕元,李志强,王 顺
(中原工学院 能源与环境学院, 河南 郑州 451191)
非织造布是用短纤维或者长丝通过纤网成型和固结技术制作的织物,具有生产工艺流程短、速度快、成本低、产量高等优良特点[1],具有广阔的应用前景[2]。非织造布可应用于过滤工业领域中的汽油、机油以及空气的过滤,生活中还能用来过滤水,还可在制药业、矿物加工业中用于液体滤芯和袋式过滤器以及真空袋的制作等[3]。现有空气过滤材料多表现出疏水性[4-5],其水蒸气透过率较低,导致高湿度条件下材料的空气阻力急剧增大,且耐清洗性能较差[6]。可知理想的空气过滤材料应满足过滤阻力低、透气性好的性质[7-8],非织造布在气体过滤领域中的应用最为广泛[9]。想要获得非织造布的阻力特性,通常需要按照纺织品织物透气性测定原理测得。多数情况下模拟工作的速度比实验工作快,可节省相当多的成本和时间[10-11]。随着计算机技术与数值计算方法的飞速发展,数值模拟已经成为与理论分析、实验研究并列的3种研究方法之一。CFD是数值模拟求解流体动力学控制方程的重要分支,通过计算机和数值计算的有效指导进行预测研究,模拟结果与实验结果吻合较好[12-14]。针刺非织造布是一种多孔结构材料。多孔介质模型可用于多孔物质,将其简化为增加阻力源项的流体区域,来避免建立复杂结构模型[15-16]。本文基于多孔介质模型从而省去建立针刺非织造布的真实结构模型,研究了针刺非织造布经过浸胶工艺处理、喷湿处理等处理方式,无尘空气流速,温湿度,厚度对其阻力性能的影响,为非织造行业对针刺非织造布的初阻力性能评估提供参考。
1 实验设备与材料
实验设备:DKS-2型多功能空气动力学实验装置如图1所示(东北制药集团沈阳市医疗器械三厂);YYT-200B斜管压力计(上海红宇电子设备厂,精度等级1);TSI5825型微差压计(上海榕申国际贸易有限公司);YM3空盒气压表(上海隆拓仪器设备有限公司);testo608-H1温湿度表(无锡美测测量技术有限公司);针刺非织造布(软质不浸胶面密度125 g/m2;硬质浸胶面密度180 g/m2;厚度1 mm,原料100%涤纶纤维,湖北绿宇环保有限公司)如图2所示。
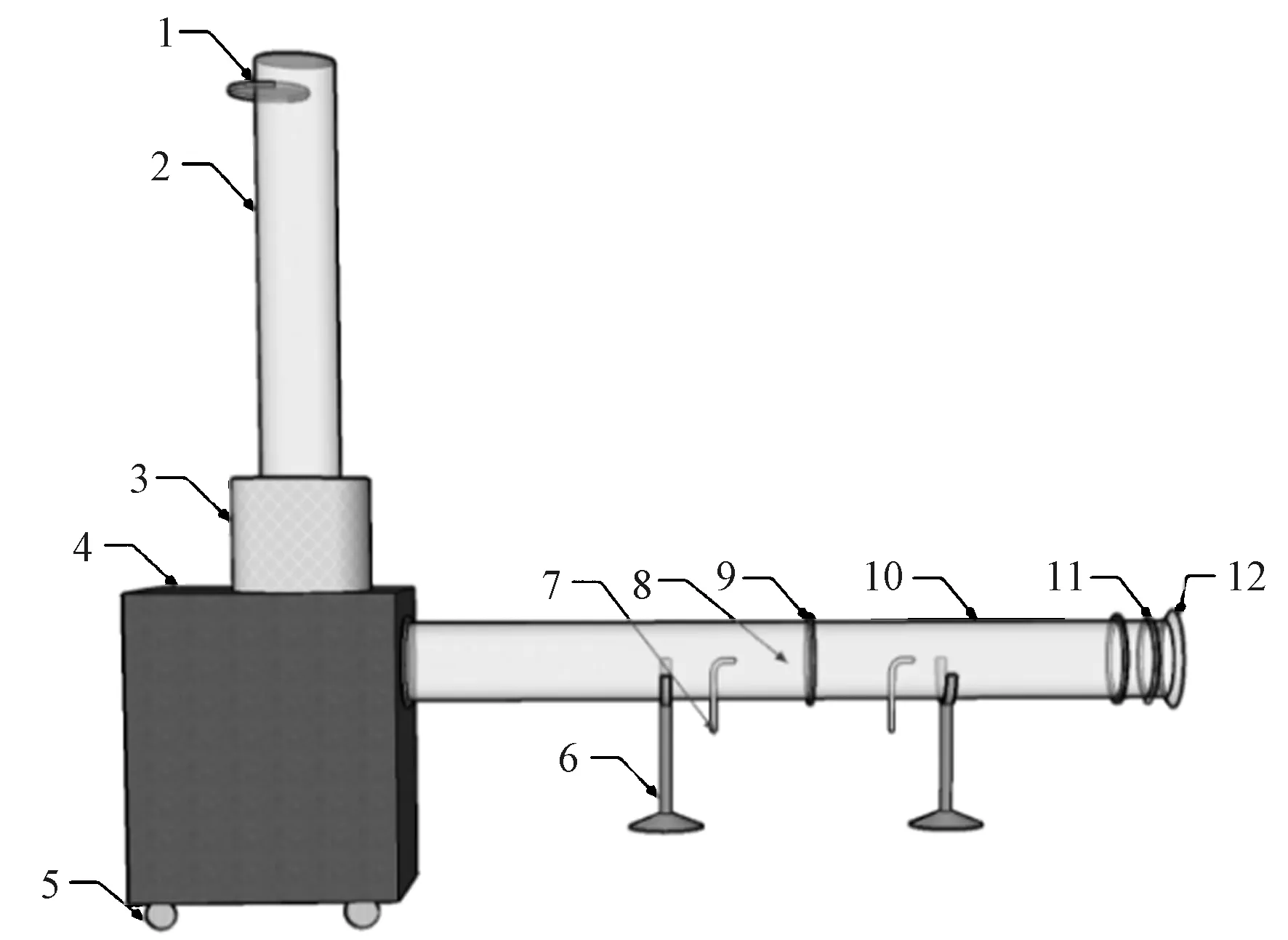
1—风量调节阀;2—出风管;3—消声器;4—机箱;5—角轮;6—支架;7—标准皮托管;8—整流格;9—法兰;10—入风管;11—取压环;12—入口。图1 DKS-2型空气动力学实验装置结构图Fig.1 Structure diagram of DKS-2 aerodynamics experimental device
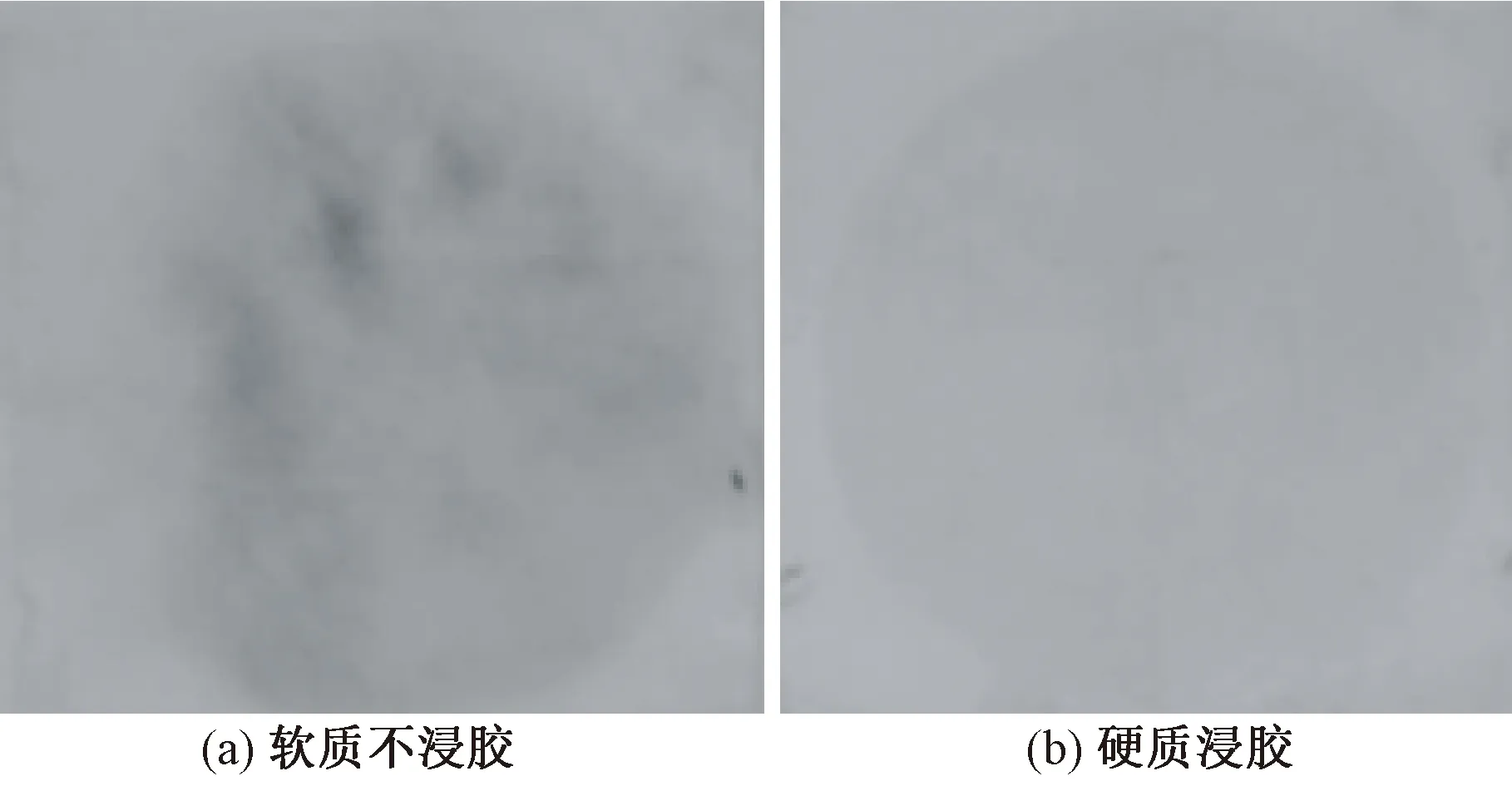
图2 针刺非织造布图Fig.2 Needle-punched nonwoven fabric drawing.(a)Soft material without gum dipping;(b)Hard material with gum dipping
DKS-2型空气动力学实验装置内,气体由入口流入,通过入风管,由出风管流出,通过风量调节阀对流速进行控制。针刺非织造布平行于入风管管道截面,安装在法兰处,空气垂直透过针刺非织造布。标准皮托管管嘴处于管道轴心,YYT-200B斜管压力计通过橡胶软管与标准皮托管连接测量压差,微差压计通过橡胶软管与取压环连接测量流速。
2 数学模型
2.1 理论方程和多孔介质模型
2.1.1 理论方程
在整个数值仿真模拟中作为连续相处理空气流体,运输过程主要是通过建立的三维模型域x、y、z向的稳态方程和动量方程确定[17]。模拟过程中不计空气能量的变化,不考虑能量守恒方程[18]。气体质量运输方程和动量守恒方程见式(1)~(4)。
(1)
(2)
(3)
(4)
式中:ρ为空气流体的密度,kg/m3;p为空气流体的压强,Pa;v为空气流体的速度,m/s;τ为应力张量,Pa;f为单位质量力,m/s2。
选用标准k-ε湍流模型来模拟空气流体的在流体域中的流动状态,通过k方程、ε方程解得[19]如式(5)(6)所示。
ρε-YM+Sk
(5)
(6)
式中:C1ε=1.44、C2ε=1.92、C3ε=0.09为模型经验常量;σk=1.0、σε=1.3为k与ε方程的无量纲参数;μ为空气流体的动力黏度,kg/(m·s);Gk、Gb为层流速度梯度与浮力引起的湍流动能,m2/s2;YM为在湍流中过度的扩散产生的波动;μt=ρCμk2/ε,为涡黏性系数;t为时间,s;xi、xj为i向与j向的坐标;Sk、Sε为用户自定义数,Sk=0,Sε=0。
2.1.2 多孔介质模型
多孔介质模型能够比较精准地模拟压损[20-21],是从多孔介质宏观流动中遵守的控制方程出发,采用数值方法来模拟研究多孔介质内的流动并得到所需结果[22]。根据针刺非织造布内部真实结构建立模型较为困难,在仿真过程中通过将针刺非织造布所在域定义为多孔介质,其余的域设置为流体域,实现针刺非织造布的压损模拟。多孔介质模型是通过在动量方程中增加一个源项来模拟多孔性的材料对流体的流阻[23],其源项由黏性阻力项和惯性损失项组成[24-26]:
(7)
式中:Si为i向源项,kg/(m2·s2);Dij、Cij为黏性阻力和惯性损失系数矩阵;|v|为流体空气的表观流速值,m/s;vi、vj为i向j向空气流体的速度,m/s。在式(5)Dij和Cij系数矩阵对角代入1/α和C2,其余为零,则动量源项方程可简化为[27-28]:
(8)
式中:α为渗透系数,m-2;C2为惯性阻力系数,可看作沿流动方向上每一单位长度的损失系数,m-1;1/α为黏性阻力系数。
2.1.3 多孔介质模型参数求解方法
用压力降与速度关系的实验数据来计算阻力系数,数据拟合为[29-30]:
p=a1v2+b1v
(9)
动量源项为多孔介质中单位长度的压降,即:
(10)
式中:Δn为厚度,m。比较式(8) (9) (10)可知:a1=ρΔnC2/2
通过函数拟合得到参数a1之后求惯性阻力系数C2,式(9)中:b1=μΔn/α
2.2 网格划分及参数设置
模型采用Multizone(多区)网格划分,网格单元尺寸、最大尺寸设置为0.005 m,模型划分为813 204个单元,842 894个节点数。网格的最大偏斜度为0.421 56,网格质量较好。网格划分如图3所示。
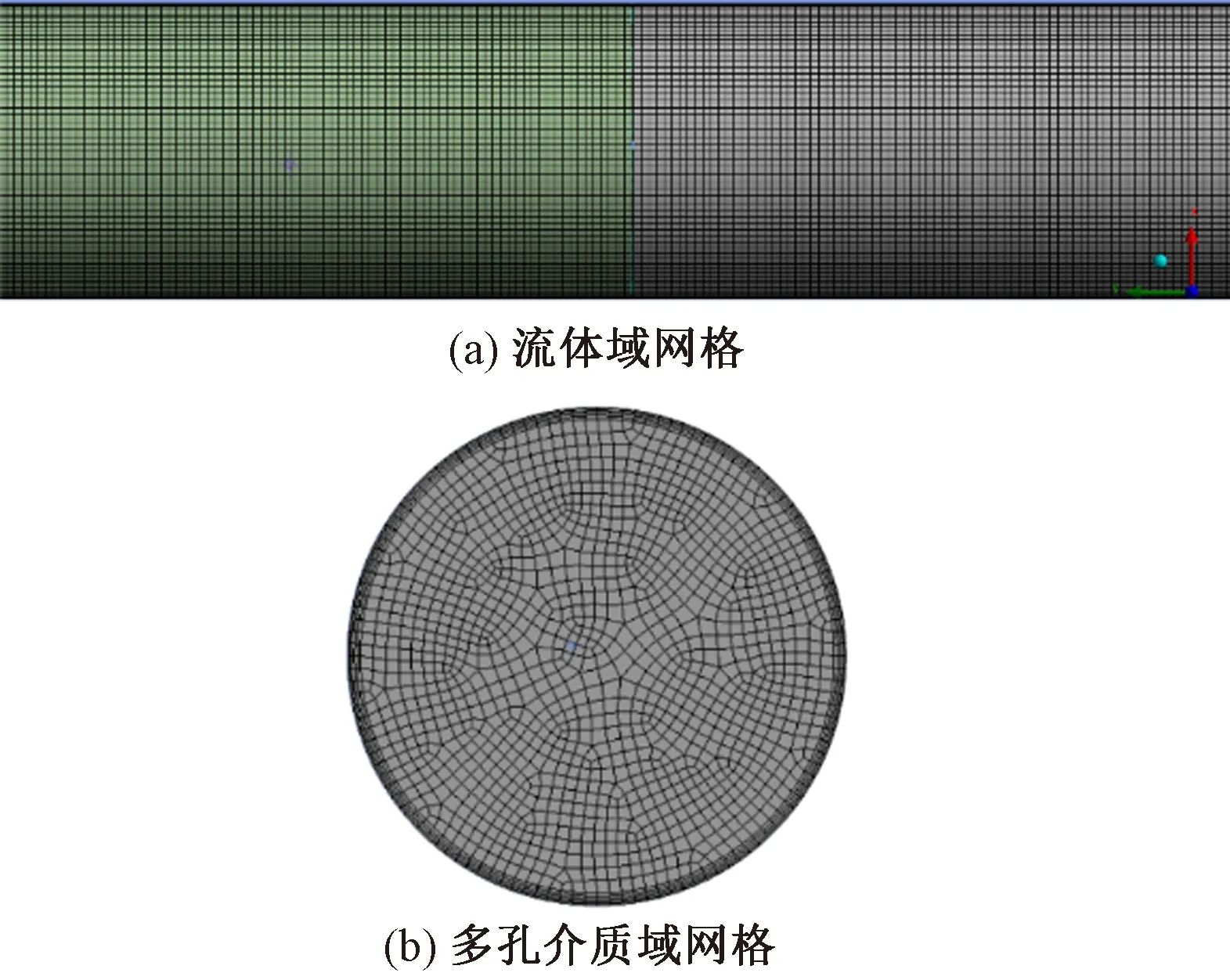
图3 网格划分示意图Fig.3 Grid division diagram.(a)Fluid domain grid; (b)Porous media domain grid
本文中空气流速处于低速气体(Ma≤0.3)范畴,可忽略空气的可压缩性。流体进口采用速度入口边界条件,出口采用压力出口边界条件,湍流强度设为5%,水力直径设为实验装置圆形风道内直径0.192 m,其余设置则选择默认值。采用标准k-ε湍流模型,壁面采用标准壁面函数。流场求解方面,压力-速度耦合采用Coupled算法,动量、湍动能和湍流耗散率选用二阶迎风离散格式,考虑残差曲线的收敛情况并选择适当的迭代步长。
2.3 网格独立无关性验证
为确保CFD仿真模拟研究数据结果的准确性,以及避免网格数量带来的数值计算误差,采取对建立的仿真模型进行一项网格独立无关性的研究分析。本文考虑仿真模型在计算时其网格划分的网格数量较小带来数值计算准确性问题及网格数量过大带来的计算时间过长的问题,考虑模型划分的网格数量在一定范围内变化,选用设计空气流体流速为2、3、4、5、6 m/s时的针刺非织造布阻力进行验证对比分析,如图4所示。可知在选取的设计流速下,当网格数量划分为50.0万时,阻力变化波动较小;当网格数量划分至81.3万个时,阻力变化波动趋于稳定,且与较少的网格数量相比阻力值相近;当网格数量划分增加至106.8万个时,阻力变化波动不大且通过增加网格数量带来的效果很小,继续增大网格数量带来的效果较小。由于网格数量的继续增加会增加计算资源的消耗且大幅增大计算时间,此时可以认为网格数量的继续增加对于计算结果的影响可以忽略[31]。通过对网格独立无关性的研究来确定网格数量和分布的适宜性,有利于得到较为准确的结果并节省计算时间。通过无关性分析最终确定网格数量划分为81.3万个。

图4 网格无关性验证Fig.4 Grid independence verification
3 计算结果与分析
3.1 流速-阻力拟合曲线
通过在设计流速下对针刺非织造布的阻力进行仿真计算。以未浸胶针刺非织造布为例,以模拟值与实验值绘出其常态和喷湿态下的流速-阻力拟合曲线,如图5所示。可以看出,仿真值与实验值相比,贴合度较高且趋势基本相同,证明本次仿真模拟中的阻力值具有很高的可信度,且流动性能几乎可以全面呈现[32]。

图5 流速-阻力拟合曲线图Fig.5 Flow velocity-resistance fitting curve
3.2 流场特性分析
设计以标准大气压下,温度为20 ℃、相对湿度30%、流速2 m/s的无尘空气为内部流体进行仿真计算,得到未浸胶、浸胶针刺非织造布在常态及喷湿态下的流场分布,如图6所示。

图6 流场截面速度和压力分布图Fig.6 Velocity and pressure distribution of flow field(a)Normal unimpregnated;(b)Unpreg inspray wet state;(c)Normal immersion;(d)Spray wet dipping
由图6可知,空气以一定速度流经针刺非织造布时,受到阻力作用,流速减小,前后形成压降;可以看出针刺非织造布喷湿、浸胶后对流体阻力作用明显增大,符合实验结果。经喷湿处理后,未浸胶针刺非织造布的独特纤维结构中存在大量水分,导致密度增大,透气性降低,对流体的阻力作用增大。对于浸胶处理后的针刺非织造布,浸胶后黏结剂在互相交错的纤维间形成黏连或成膜,透气性降低,阻力增大,喷湿后更大。由图6(a)(b)可看出,未浸胶的针刺非织造布,在常态、喷湿态下的速度场分布相似,喷湿处理对速度场分布无明显改变,但会增大对流体的阻碍作用,导致压降增大;由图6(a)(c)可看出,针刺非织造布经浸胶处理后,速度分布与未浸胶针刺非织造布相差较大,可知经过浸胶工艺处理后,纤维致密度的提高对流体通过有较大影响,由图6(d)可看出喷湿后影响会更大。对针刺非织造布正反2面压力进行研究,绘制表面压力分布云图,如图7所示。

图7 针刺非织造布表面压力分布云图Fig.7 Surface pressure distribution nephogram of needle-punched nonwovens. (a) Normal unimpregnated fluid surface; (b) Normal non-dipped fluid surface; (c) Spray wet unimpregnated fluid facing; (d) Unimpregnated fluid surface in spray state; (e) Normal dipping facing fluid surface; (f) Normal leaching fluid surface; (g) Spray wet dipping facing; (h) Extruded fluid surface by spray-wetting
针刺非织造布的独特纤维网层结构,内部纤维随机排布,空气流体流经针刺非织造布时,互相交错的纤维会使空气绕行,产生阻力。由于边界层存在,紧靠圆管壁面附近,流速较势流流速急剧减小,流体流进针刺非织造布边缘区域时的速度与中心流体区域相比会较小,且会受到针刺非织造布的阻力,形成边缘区域压力较中心域会更大的现象,且喷湿后造成的压力较常态会更大,图7(a)(c)(e)(g)很好的展示了这一现象。如图7(b)(d)(f)(h)所示,当流体流出针刺非织造布多孔介质区域时,在近壁面处流体不会受到针刺非织造布阻力的作用,壁面处流速会相对增大,边缘区域压力会变小。
为更好的展现针刺非织造布表面压力分布特性,以未浸胶针刺非织造布常态和喷湿态为例,绘出多孔介质表面中轴线压力随距离的变化曲线,如图8所示。可以看出多孔介质表面中轴线压力曲线进一步证实了上述的针刺非织造布表面压力分布特性。通过对整个流场阻力进行研究,绘制流场轴心压力分布曲线,如图9所示。从曲线图可明显看出流体流经针刺非织造布时,阻力会出现明显升高的特性。
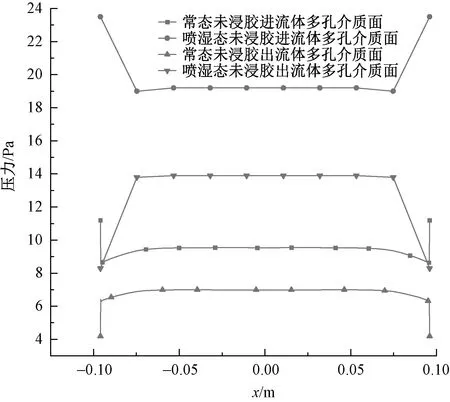
图8 多孔介质表面中轴线压力随距离的变化曲线 Fig.8 Variation curve of axial pressure with distance on porous media surface

图9 实验装置中心压力随距离的变化曲线Fig.9 Variation curve of center pressure of experimental device with distance
3.3 空气温湿度对阻力的影响
通常的空气是含有一定数量水蒸气的湿空气,进行以湿空气为工质的流动计算时,需要确定其热物理性质的数值,实验时湿空气动力黏度由拟合方程[33](11)计算:
μ=(8.180 4+4.011×10-2t-1.785 8×
10-5t2)×10-6
(11)
湿空气密度[34]为:
(12)
式中:ρs为湿空气密度,kg/m3;pq,b为饱和空气水蒸气分压力,Pa;pa为大气压力,Pa;T为湿空气的热力学温度,K;φ为空气相对湿度,%。
设计标准大气压下,研究浸胶、未浸胶针刺非织造布在常态及喷湿态下,阻力随无尘空气温度、相对湿度的变化。以流速2、3、4 m/s为例绘制出阻力随空气温度、相对湿度的变化,如图10所示。
由图10可知,无尘空气流经常态、喷湿态针刺非织造布时,流速越大,阻力越大;浸胶处理、喷湿处理会明显增大阻力;在研究的温湿度范围内,流速越大,上下限阻力差值波动幅度越大。浸胶、未浸胶针刺非织造布在常态及喷湿态时,当温度、流速一定条件下,湿度增大,阻力减小。由式(12)可知,在大气压强、温度一定时,空气中水蒸气含量越大,即φpq,b值越大,湿空气的密度越小,原因在于空气的分子量大于水的分子量,由式(11)可知当温度恒定时,湿空气动力黏度不变,因此在温度、流速一定条件下,阻力随相对湿度增大而减小的原因在于空气湿度的增大导致的空气密度的减小。通过针刺非织造布阻力随温度湿度变化图可知,在50~100 ℃温度区间内,在流速、温度一定条件下,相对湿度增大,阻力显著减小;在0~50 ℃温度区间内,在流速、温度一定条件下,相对湿度增大,阻力无明显减小。可知在0~50 ℃温度区间内,流速、温度一定时,相对湿度对非织造布阻力影响较小。如图11所示,在0~50 ℃温度区间内,相对湿度的变化对空气密度影响较小,原因在于饱和空气的水蒸气分压力pq,b较小,相对湿度对空气密度的影响较小,因此对针刺非织造布的阻力变化影响不大。对于未浸胶常态、喷湿态针刺非织造布及常态浸胶针刺非织造布,可以看出在流速、相对湿度一定条件下,温度增大,阻力增大;喷湿态浸胶针刺非织造布在流速、相对湿度一定条件下,温度增大,阻力减小。当空气流速和相对湿度一定时,随着空气温度的升高,空气密度虽然会减小,但空气的动力黏度会随着温度的升高而变大,此时空气动力黏度随温度升高而增大是未浸胶常态、喷湿态针刺非织造布及常态浸胶针刺非织造布阻力增大的主导因素;对于喷湿态浸胶针刺非织造布在流速、相对湿度一定条件下,阻力随温度的增大而减小,推测浸胶针刺非织造布在喷湿态下,纤维间的膜状物与水分相互作用形成的内部结构,使其阻力受流体密度的影响较大。

图10 针刺非织造布阻力随温度湿度变化图(v=2,3,4 m/s)Fig.10 Diagram of resistance of needle-spun nonwovens with temperature and humidity(v=2,3,4 m/s). (a) Normal unimpregnated needle-punched nonwovens; (b) Needle-punched nonwovens in wet state; (c) Normal dipping needle-punched nonwovens; (d) Needle-punched nonwovens with wet-jet dip adhesive
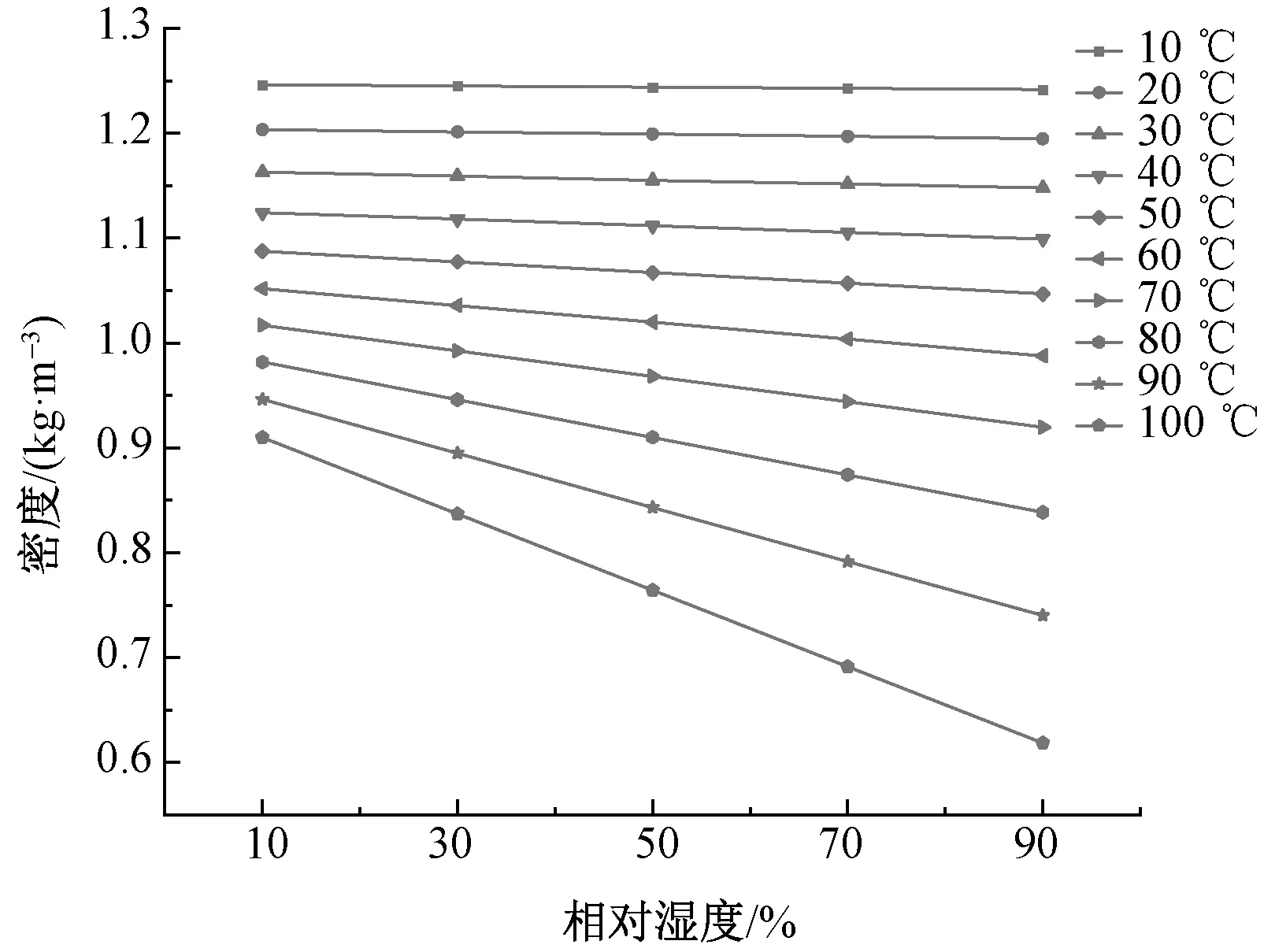
图11 空气密度随湿度变化曲线Fig.11 Curve of air density with humidity
总体来看,在50~100 ℃温度区间内,当空气的流速、温度一定时,相对湿度对阻力有显著影响。在0~50 ℃温度区间内,相对湿度对阻力无明显影响。对于未浸胶常态、喷湿态针刺非织造布及常态浸胶针刺非织造布,在流速一定时,温度越低,相对湿度越大,阻力越小;而对于喷湿态浸胶针刺非织造布,在流速一定时,温度越大,相对湿度越大,阻力越小。
3.4 流速和厚度对阻力的影响
以标准大气压下,温度为20 ℃、相对湿度30%的无尘空气为内部流体,研究不同流速和厚度下未浸胶、浸胶针刺非织造布在常态及喷湿态时的阻力,如图12所示。

图12 阻力随流速和厚度变化曲线Fig.12 Curve of resistance with flow velocity and thickness.(a)Unimpregnated needle-punched nonwovens;(b)Dipping needle-punched nonwovens
由图12可知,喷湿对浸胶针刺非织造布的阻力性能影响更大。原因可能是,浸胶后的针刺非织造布纤维间与膜状物间充斥着大量水分,在水分与膜状物的双重作用下对整体透气性影响更大,阻力变化更大。针刺非织造布的厚度影响阻力,但厚度越大不代表阻力越大,二者虽然有密切关系,但阻力大小还取决于流体流速等。在流速一定条件下,阻力与厚度呈正相关;在厚度一定条件下,阻力与流速呈正相关。对变化曲线的数据进行分析,浸胶、未浸胶针刺非织造布在常态及喷湿态下,当流速一定时,厚度规律性增大,阻力之间的差值近似为定值。故在流速一定条件下,通过测定同一类型,厚度不同的针刺非织造布阻力即可得到这个定值,记为u。通过这个定值u,估算相同流速下厚度不同的针刺非织造布阻力,偏差不超过2%。在流速、厚度同时规律性增大时,u与流速呈二次函数关系,与流速呈正相关,可拟合为u=a2v2+b2v,a2、b2为拟合系数。以图12为例:ua常态=0.188 3v2+0.897 2v,ua喷湿态=0.200 4v2+2.641 8v,ub常态=0.894 0v2+2.423 9v,ub喷湿态=4.610 0v2+4.158 9v。常态和喷湿态下的浸胶、未浸胶针刺非织造布,在厚度一定时,规律性的增大流速,阻力之间的差值近似等差数列。可通过测试3组不同流速下针刺非织造布阻力,即可推出其它流速下的阻力,推测出的阻力与真实值之间偏差不超过30%。
4 结 论
本文采用CFD流场数值模拟方法,基于多孔介质模型研究了无尘空气的流速、温度、湿度对针刺非织造布初阻力性能的影响;在此基础上对浸胶、喷湿、厚度与阻力之间的关系进行分析。得出以下结论:
①基于CFD计算得到的阻力模拟值与实验值相近,流速-阻力曲线的贴合度较好,趋势相同,符合实际情况;证明了数值模拟研究数据的准确性,能有效地获取压力场、速度场,并进行研究分析。
②浸胶、喷湿会增大针刺非织造布阻力,浸胶对针刺非织造布阻力的影响更大。在温度、流速一定条件下,相对湿度增大,阻力减小;且在50~100 ℃温度区间内,增大相对湿度,阻力会显著减小,在0~50 ℃温度区间内,阻力不会明显减小。常态、喷湿态未浸胶及常态浸胶针刺非织造布,在流速、相对湿度一定时,温度增大,阻力增大;喷湿态浸胶针刺非织造布则在流速、相对湿度一定条件下,温度增大,阻力减小。
③针刺非织造布的阻力与流速、厚度呈正相关。在流速一定时,厚度规律性增大,阻力之间的差值近似为定值。通过定值估算相同流速下厚度不同的针刺非织造布阻力,估算偏差不超过2%。常态和喷湿态下的浸胶、未浸胶针刺非织造布,在厚度一定时,规律性的增大流速,阻力之间的差值近似为等差数列。可通过测试3组规律性流速下的阻力来推测其它流速下阻力,推测偏差不超过30%。研究结果可为针刺非织造布初阻力性能评估和预测提供参考。

