内置转子圆管管内沸腾强化传热数值模拟研究
黎昊为 左夏华 张岱凌 温 馨 阎 华 杨卫民
(北京化工大学 机电工程学院,北京 100029)
引 言
蒸发器作为换热器的一种,广泛应用于石油、化工和核电等工业领域。针对蒸发器的强化传热开展结构及其机理的研究对提高能源利用效率、降低投资成本具有十分重要的意义[1]。
换热管用于两种介质的热量交换,是蒸发器的主要组成部件。根据强化传热方式的不同,可以将强化传热技术分为异型管强化法和内插件强化法[2],研究人员对这两种技术在沸腾传热过程中的表现进行了研究。党高健等[3]以煤油和水为工质,对不同流速下波纹管和光管的沸腾传热性能进行实验研究,发现当工质为煤油时波纹管的管内沸腾传热系数是光管的2~4倍,当工质为水时,波纹管的管内沸腾强化传热系数是光管的7~14倍。李豪[4]通过数值模拟的方法研究了波节管的沸腾传热性能,结果表明波节管在沸腾过程中的表面换热系数明显高于光管,并且其沸腾恶化点相较于光管滞后。刘萍等[5]发现在光管内插入纽带后,其管内沸腾传热系数比光管提高了6%~90%。牛志愿[6]采用在管内插入金属丝网管的方式进行了管内水流动沸腾的可视化研究,结果表明金属丝网管可提高部分流型的局部传热系数,最大强化沸腾传热系数可提高3倍以上。总体上来看,异型管强化法相较于内插件强化法具有适应性强、压降损失小等优势,但是其内表面污垢难以清理,加工难度较大。内插件强化法虽然会导致压降的增加,但是具有成本低、易安装、可在线清洁等优势[2],更适用于蒸发器内沸腾工况下易结垢的环境。
组合转子是一种内插件式强化传热技术,相较于螺旋纽带,其强化传热性能与阻垢性能有明显提升[7-8]。本课题组已通过实验和数值模拟的方式,对内置单元组合转子换热管的综合传热性能及阻垢特性进行了一系列研究[9-13]。但是以往的研究尚未涉及到管内沸腾相变的工况。换热器管管内沸腾是指管中液体在流经换热管管壁时,与管壁产生热交换从而发生的沸腾现象,沸腾过程中产生的气泡无法自由上浮,而是与管中的液体发生混合,随着加热过程的进行,其流动形式以及换热模式也会发生一定的变化[14-15]。与无相变的对流换热相比,沸腾伴随着潜热的吸收,两者的换热系数有较大差别。本文通过Fluent中的Rensselaer Polytechnic Institute(RPI)沸腾模型对内置组合转子换热管的管内沸腾传热进行模拟,主要探究了不同流速下内置螺旋三叶片转子以及低流阻转子管内的汽相体积分数以及传热性能,以期为进一步的研究工作乃至工业应用提供借鉴。
1 数值计算
1.1 物理模型的建立
内置组合转子换热管结构如图1所示。转子通过转轴串起并用挂件固定于换热管两端,数个转子通过限位件的方式被分成不同的组,转子在管内水流的冲击作用下转动并悬浮于管中,转子的旋转带动周围流体做螺旋运动,加剧了管内介质的湍流程度,大大减薄边界层,在强化传热的同时具有在线除垢的功能。
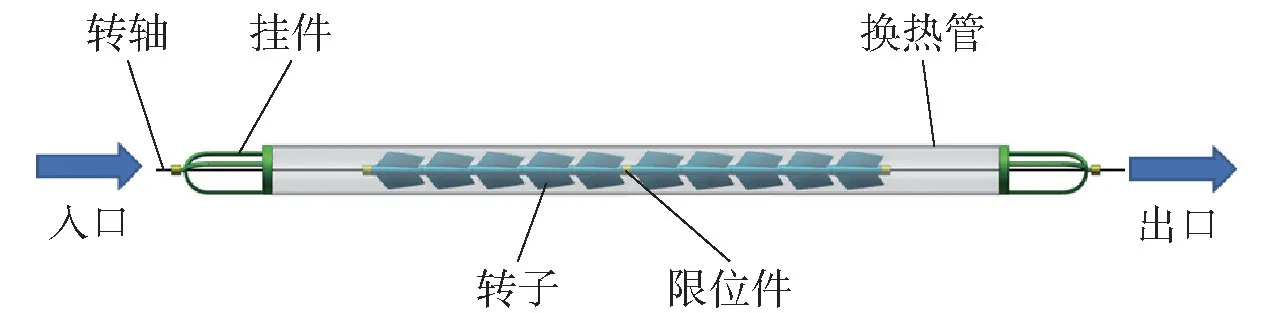
图1 内置转子换热管结构示意图Fig.1 Structure of the circular tube with inserted rotors
利用Solidworks软件建立内置转子换热管模型,由于限位件、挂件、转轴对管内流动与传热的影响较小,为简化计算过程,在所用模型中予以删除,并忽略换热管壁厚。选取5个转子组成为转子串,转子外径为17 mm,导程为200 mm,换热管管长为200 mm,内径为19 mm,模型如图2所示。采取相同方法建立内置低流阻转子换热管模型,低流阻转子结构如图3所示,转子外径为10 mm。采用四面体网格对模型进行划分,以进出口压降来考核网格的独立性,网格独立性检验结果如图4所示,综合考虑精度与计算时间,分别选取1133018和1410812作为内置螺旋三叶片转子换热管模型和内置低流阻转子换热管模型的网格数。
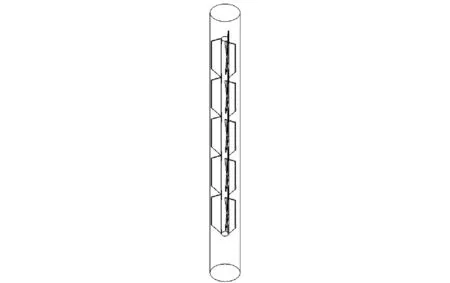
图2 内置组合转子换热管模型Fig.2 Model of the circular tube with inserted rotors

图3 低流阻转子结构示意图Fig.3 Structure of the low flow resistance rotor
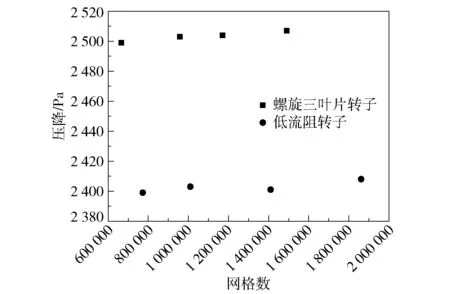
图4 网格独立性检验结果Fig.4 Grid independence test results
1.2 计算模型的选择
由于管内的沸腾过程涉及液态水向水蒸汽的相变过程,是典型的两相流动,所以需选用多相流模型。本文选取欧拉多相流模型中的RPI沸腾模型,同时选用Ishii模型来模拟沸腾状态下两相间的相互作用[16]。RPI模型将加热面传递给流动介质的热通量qw分成了3个部分,分别为液相对流传热通量qc、蒸发传热通量qE和气泡脱离处由于液体冲击壁面引起的激冷传热qQ,关系式如下。

式中,hc为单相对流传热系数,Tw为换热管壁面温度,Tl为液体温度,kl为液相导热系数,t为气泡等待的时间周期,f为气泡脱离频率,λl为扩散系数,dw为根据关系式计算得出的气泡脱离直径,Nw为气化核心密度,ρv为气体密度,ifg为产生蒸汽的汽化潜热,A1为壁面上液相所占面积分数,A2为壁面上汽相所占的面积分数,二者关系为

其中Dw为管壁直径。
湍流模型选用对瞬变流和流线弯曲影响预测能力较好的重整化群(renormalization group,RNG)k-ε模型,并选择标准壁面方程。
1.3 边界条件的设置
本文模拟过程的边界条件如下。
1)入口边界采用速度进口条件,进口速度分别取0.1、0.2、0.3、0.4 m/s和0.5 m/s,入口流体全部为水,流体温度为370.15 K,蒸发温度为373.15 K。
2)出口设置为压力出口边界条件。
3)壁面采用恒壁温加热条件,设置温度为378.15 K。
4)设置重力方向沿管轴线向下,即管子竖直放置,流体由下端进入,向上流动。
1.4 求解器的设置
本文选用压力基求解器,压力速度耦合采用Coupled算法,对湍流动能的离散格式采用一阶迎风差分格式,动量以及湍流耗散率方程的离散格式采用二阶迎风差分格式,体积分数方程采用Quick格式。管中汽相体积分数不再变化,且连续性方程、动量方程和能量方程的残差分别达到10-4、10-6、10-6时即认为收敛。
2 结果与讨论
2.1 入口速度对汽相体积分数的影响
内置单元转子换热管和光管在不同入口流速下的汽相体积分数对比如图5所示。由图5可知,无论是光管还是强化管,其管中汽相体积分数都随入口流速的增大而减小,这是由于随着入口处冷流体流速的增加,冷流体与换热管壁的换热时间减少,无法得到充分的加热并沸腾,导致管中的汽相体积分数减小。此外,不同入口流速下内置单元转子换热管中的汽相体积分数均大于光管的汽相体积分数;在入口流速为0.1~0.5 m/s范围内,随着流速的降低,内置螺旋三叶片转子换热管内汽相体积分数较光管增大2.7%~25.8%,内置低流阻转子换热管内汽相体积分数较光管增大1.13%~13%,说明加装单元组合转子后换热管的沸腾效果有所提升。

图5 汽相体积分数随入口流速变化的关系曲线Fig.5 Variation in vapor volume fraction with inlet velocity
2.2 不同位置处汽相体积分数的对比
图6给出了在入口流速为0.3 m/s时汽相体积分数沿轴线距入口处位置的变化情况。可以看出,随着流体与管壁换热过程的进行,管中流体的温度逐渐升高,3种管的汽相体积分数沿轴线方向呈递增的趋势。对于加装单元组合转子的换热管,在入口段过渡区的汽相体积分数与光管的差别较小,但在0.04 m之后,流体抵达组合转子的作用区,内置螺旋三叶片转子换热管内的汽相体积分数相对于光管有11%~27.8%的提升,内置低流阻转子换热管内的汽相体积分数相对于光管提高约5.1%~13.2%。

图6 汽相体积分数随轴向位置的变化曲线Fig.6 Variation in vapor volume fraction with position
2.3 典型截面分析
图7给出了入口流速为0.3 m/s时3种管在同一位置截面处的汽相体积分数分布云图。在加装螺旋三叶片转子后,管壁处生成的换热系数较小的蒸汽在旋流扰动下脱离壁面,并被转子裹挟至管中心区域,壁面附近的换热系数较大的液态水得以更充分地与壁面进行热交换,极大地促进了沸腾过程的进行。低流阻转子由于叶片尺寸较小,作用范围小,其对蒸汽的裹挟作用不及螺旋三叶片转子明显,但相较于光管还是可以很明显地看出在管壁附近汽相分布更加均匀。

图7 3种管的汽相体积分数分布云图Fig.7 Distribution contours of the vapor phase volume fraction for three kinds of tubes
图8所示为3种管沿管长方向纵向截面的汽相体积分数分布云图。水自下而上以一定过冷度进入换热管。可以看出,水在内置转子换热管中起始沸腾点的出现位置均先于光管,内置转子换热管的起始沸腾点约在第一个转子的作用区附近;且相较于低流阻转子,螺旋三叶片转子的扰动作用更加剧烈,其沸腾起始点的出现位置更早。从整体来看,可以发现加装转子后管中蒸汽的分布更均匀,水汽混合更加充分,由此可以说明沸腾工况下,组合转子对于汽液两相流的传质有提升作用。
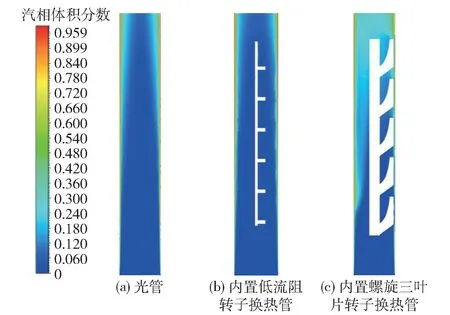
图8 3种管沿管长方向纵向截面的汽相体积分数云图Fig.8 Contours of the vapor phase volume fraction for three kinds of tubes(longitudinal section along the pipe length)
图9所示为3种管在同一截面处流场的速度云图。可以看出在加装了转子后,靠近叶片处流场的流速有了极大的提升,形成较强的旋流,旋流的产生对速度边界层造成破坏,从而增强了流体与壁面间的换热。
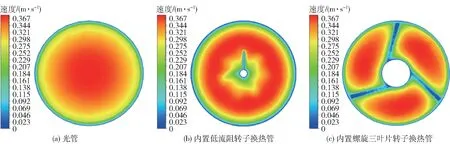
图9 3种管流场速度云图Fig.9 Contours of the velocity field for three kinds of tubes
图10为内置螺旋三叶片转子换热管与光管的流场流线图。通过对比可以看出,流体在进入加装转子的换热管后,很快便开始了螺旋运动,流体既具有径向速度也具有轴向速度,在径向流和轴向流的共同作用下,冷热流体得到了充分的热交换,加速了对流换热。从光管的流线图可以看出,其内部仅有轴向流,难以对边界层造成扰动。

图10 两种管的流场流线图Fig.10 Flow field streamline diagrams for two kinds of tubes
2.4 强化传热综合性能评价
图11是内置单元组合转子换热管和光管在不同入口流速条件下的努赛尔数Nu的变化情况对比。由图可见,在不同的入口流速下,内置螺旋三叶片转子换热管的Nu明显高于光管,提高幅度约在8.1%~10.79%,内置低流阻转子换热管相较于光管其Nu提高约3.6%~8%,说明单元组合转子对传热有一定的强化作用。这是由于内置单元组合转子后,管中的流体在转子叶片的作用下被甩向壁面,破坏了边界层,湍流程度大大提高,加剧了中心部位的流体与换热管壁的热交换[17],从而提升了传热效率。

图11 3种管的Nu对比曲线Fig.11 Comparison of Nu for three kinds of tubes
图12是3种管在不同流速下的进出口压降对比。由图可见,内置单元组合转子换热管和光管的进出口压降均随着入口流速的增大而提高,且内置螺旋三叶片转子换热管的压降要远远高于光管压降;内置低流阻转子换热管的压降低于内置螺旋三叶片转子换热管,并且两种强化管内的压降上升更快。这是由于转子的旋转带动周围的流体形成二次流,令边界层附近流速较低的流体与中心处的流体混合,增大了摩擦阻力所做的耗散功,同时流通面积的减小也会使得阻力增大[18]。
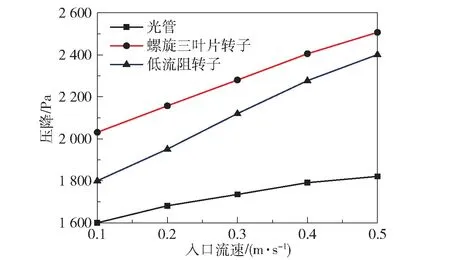
图12 3种管的压降对比曲线Fig.12 Comparison of pressure drops for three kinds of tubes
综上所述,内置单元组合转子后,在换热管传热能力增大的同时,也增大了进出口压降,引入了更大的流动阻力,因此以综合评价因子F(PEC)为指标对换热管的传热效果及节能效果进行衡量[19]

式中,Nu、f分别表示内置单元组合转子换热管的努塞尔数和阻力系数,Nu0、f0分别表示光管的努塞尔数和阻力系数。两种内置单元组合转子换热管的PEC结果如图13所示。
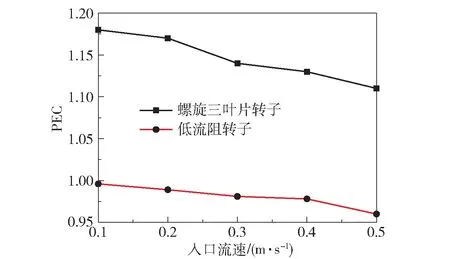
图13 内置单元组合转子换热管的综合评价因子Fig.13 PEC of tube with inserted rotors
由图可知,在模拟范围内内置螺旋三叶片转子换热管的PEC值均大于1,内置低流阻转子换热管的PEC值均小于1,因此综合比较而言,螺旋三叶片转子的强化传热性能更优。
3 结论
(1)本文模拟范围内,内置螺旋三叶片转子换热管、内置低流阻转子换热管相较于光管在过冷沸腾工况下,其管内汽相体积分数分别提高了约2.7%~25.8%和1.13%~13%,在入口流速为0.3 m/s时,沿管轴线处的汽相体积分数有11%~27.8%和5.1%~13.2%的提升。对几种换热管典型截面的汽相分布云图进行分析后发现,在内置单元组合转子后,汽液两相流的传质效果有明显提升。
(2)内置转子后,换热管管内流体的流动方式发生了明显的变化,由简单的轴向流动转变为复杂的螺旋运动,使边界层得到了充分扰动。
(3)两种强化管的努塞尔数相较于光管均有一定的提高,其中内置螺旋三叶片转子换热管的努塞尔数大于内置低流阻转子换热管;此外,加装转子会引入更大的阻力,低流阻转子带来的阻力要低于螺旋三叶片转子。通过综合评价因子对两种强化管的换热性能进行衡量,发现在模拟范围内内置螺旋三叶片转子换热管的PEC值均大于1,内置低流阻转子换热管的PEC值均小于1,因此螺旋三叶片转子的强化传热性能更优。

