储液晃动对卧式储罐地震响应的影响研究
崔利富,孙建刚,吕 远,程丽华
(1.大连民族大学土木工程学院,辽宁大连 116605;2.哈尔滨工业大学(深圳)土木与环境工程学院,广东深圳 518055;3.广东省石油化工腐蚀与安全工程技术研究中心,广东石油化工学院,广东茂名 525000)
引言
卧式储罐通常用于石化行业,用于储存低温,高压化学原料,工艺材料和成品。由于卧式储罐中的液体储存通常具有高毒性,易燃性和爆炸性的特点,一旦强烈地震破坏,可能会导致严重的继发性灾难,例如爆炸和火灾。在地震作用时,卧式储罐的地震响应十分复杂的,包括支承结构及罐体振动、储罐晃动以及液固耦合振动等。目前,国内外学者针对储罐结构的抗震设计、储液晃动等研究多关注于立式储罐或LNG储罐[1-10],而现有卧式储罐地震响应问题的参考文献相对较少,且外文文献居多。2005年,Platyrrachos和Karamanos[11]针对卧式储罐晃动问题提出了一种基于理想状态(无自旋,无粘性,小晃动)的液体晃动的有限元计算公式。2008年,Stefan[12]研究了水平圆柱形储罐中粘性液体的晃动形状和晃动频率,并得出了不同储水高度和储水粘度下的轴向和横向晃动频率。2009年,Karamanos[13]假设液体为理想流体,并通过有限元方法求解了液体速度势。通过分解储罐-液体运动,提出了一种计算晃荡频率和晃荡当量的有效方法。2012年,Omar Badran[14]提出了水平罐的三维准静态集中质量模型,并研究了其在加速状态下的动态性能。2015年,Amir Kolaei[15]提出了结合多峰方法的边界元法,并研究了油轮在制动和转向过程中横向和纵向加速度激励的三维晃动问题,并进一步讨论了其适用性。2016年,Wenyuan Wang[16]基于线速度势理论,推导了新的变分原理公式和半解析缩放边界有限元方法来解决液体的晃动问题。2017年,Seyyed M.Hasheminejad[17]基于线速度势理论和圆柱贝塞尔函数推导了水平储罐晃荡的解析解。2018年,Alessandra Fiore[18]进行了水平罐动态分析和安全验证,并基于有限元模型建立了单自由度简化的力学模型。2020年,吕远等[19]立足于卧式储罐抗震设计,基于势流体理论推导了横向与纵向地震激励时的抗震设计简化力学模型。
综上所述,当前卧式储罐抗震设计研究的关键问题为液体晃动,且多依靠理论分析与有限元数值仿真技术,试验研究较少。鉴于此,本文以卧式储罐为研究对象,采用理论分析与模拟地震振动台试验相结合的方式,重点分析横向地震激励下液体的晃动对卧式储罐地震响应的影响,结合振动台试验对比验证简化力学模型以及规范算法,为卧式储罐抗震设计提供理论与试验支撑,对卧式储罐的抗震设计具有一定的指导意义。
1 考虑储液晃动的简化力学模型
以卧式储罐圆柱形罐壁轴线为Z轴,建立如图1所示柱坐标系。依据势流体理论,将储液简化为无漩、无粘、不可压缩的理想流体,其速度势Φ( )r,θ,z,t满足Laplace方程。忽略罐壁的弹性变形,将其假定为刚性罐壁,则储液速度势可分解为随罐壁振动的刚性速度势Φr( )r,θ,z,t以及晃动速度势Φs( )r,θ,z,t。根据流体动力学,求解液体动态压力的关键问题在于求解储液运动速度势。根据本文假定,储液速度势为Laplace方程的边值问题。
横向地震激励时,从边界条件很容易知道,储液速度势是一个关于r和θ的二维问题,储液液罐壁接触面满足如式(2)~式(3)的边界条件,而在自由液面满足边界条件(4)[17]。
式中:x g(t)为地面位移;x0(t)为由卧式储罐支承结构变形引发的罐壁位移。
结合边界条件,求解极坐标系下Laplace方程,并结合结构动力学振型叠加法克推得储液运动速度势的表达式。
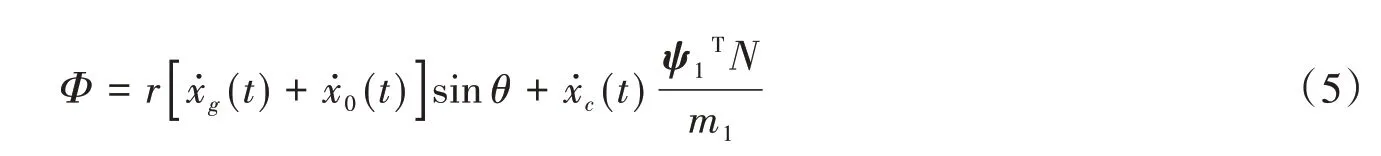
式中,ψ1为液体晃动第1阶振型向量;N=[r nsin(nθ)]n×1,m1为第1阶晃动振型对应的广义质量。
根据储液运动速度势,可进一步推得重力场作用下自由液面的振动形态(液体晃动波高),及储液作用在罐壁上的动液压力:

则其中ρ为储液密度。
将储液动态压力在液固耦合面域内积分并加上罐壁惯性力即可得地震作用下,卧式储罐支承(鞍座)承受的水平剪力:
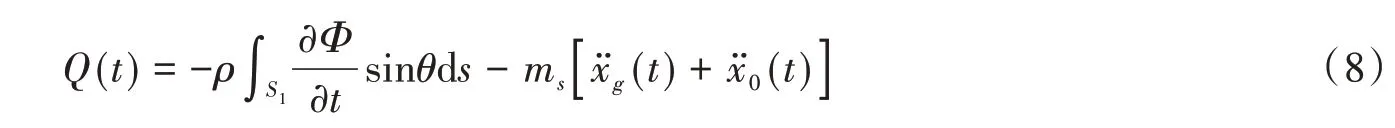
式中,m s为罐壁等的等效质量。通过积分变换,等式(8)可转化为:
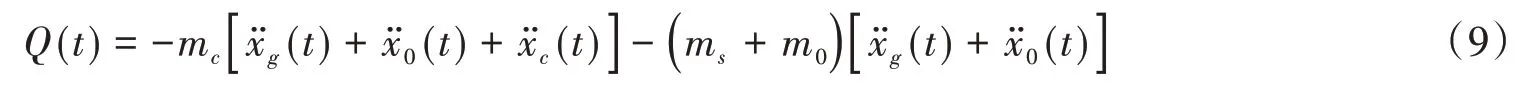

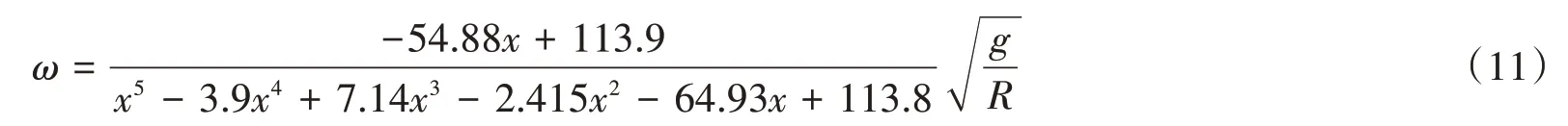
则根据式(9)即可构建横向地震激励下卧式储罐考虑储液晃动的简化动力学模型[17],如图2所示。mr为储液刚性分量等效质量与罐壁等质量之和。
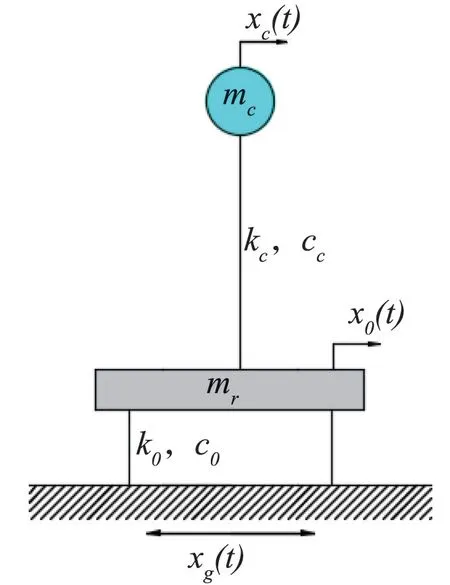
图2 简化动力学模型Fig.2 Simplified kinetic model
其中,k c,c c分别为晃动分量等效刚度系数和阻尼系数,可表示为:


式中,k0,c0为支承结构等效刚度系数和阻尼系数。ξ为晃动等效阻尼比。
由Hamilton原理,可推导建简化力学模型的运动方程式。根据能量守恒,存在:

式中:T,V分别为系统的动能和势能;W为非保守力做的功。解得:
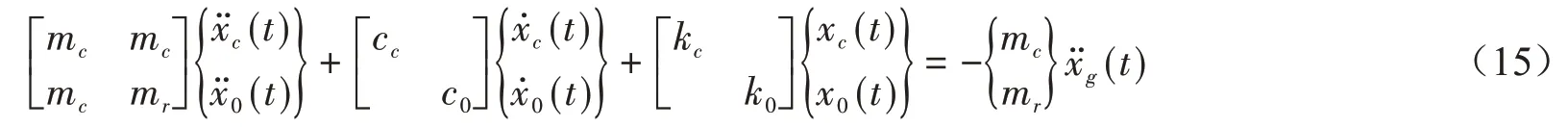
2 单质点简化力学模型
目前,国内涉及卧式储罐抗震设计的规范均未考虑储液晃动影响,即将卧式储罐简化为单质点体系[20~22],如图3所示。
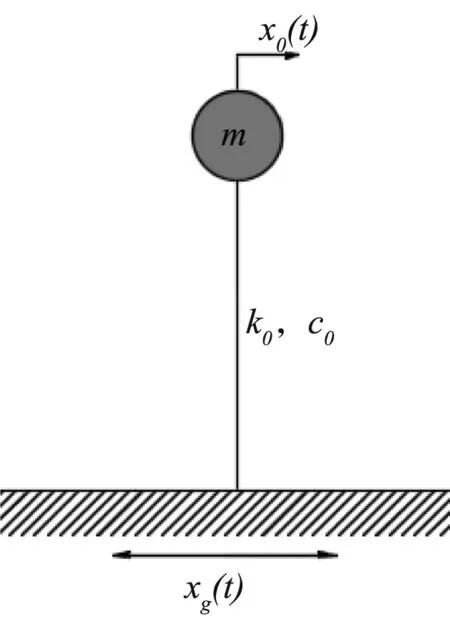
图3 单质点简化动力学模型Fig.3 Simplified kinetic model of single particle
式中,m为储液质量,罐壁质量及其他附件质量总和。其地震响应运动控制方程为:

地震作用时上部结构作用于鞍座的水平惯性力为:

3 数值算例分析
选取某一回流卧式储罐作为算例,进行数值分析。储罐全容积为7 m3,充装系数为0.85,设计压力:常压,存储介质为水混合物,可认为其密度为1 000 kg/m3。罐体内径为1 500 mm,壁厚6 mm,罐体总长3 312 mm,圆柱形罐体长2 550 mm,两端为标准椭圆封头。鞍座包角为120°,材料为Q235钢材。卧式储罐具体参数如图4所示。
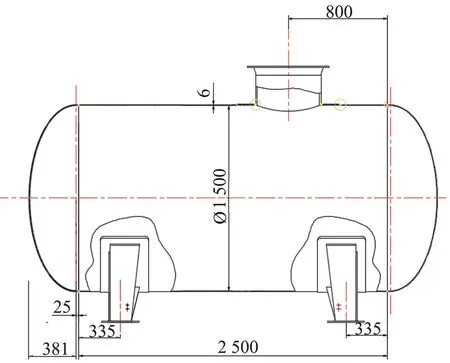
图4 卧式储罐示意图(单位:mm)Fig.4 Schematic diagram of horizontal storage tank
3.1 地震动输入
石油化工钢质设备抗震设计规范(GB 50761-2012)[22]将地土大致分为Ⅰ,Ⅱ,Ⅲ,Ⅳ四种类型,因此根据规范本文针对每类场地选取对应的3条实际记录地震波作为地震动输入,并调整PGA=0.2 g。其加速度响应谱和标准谱如图5所示。
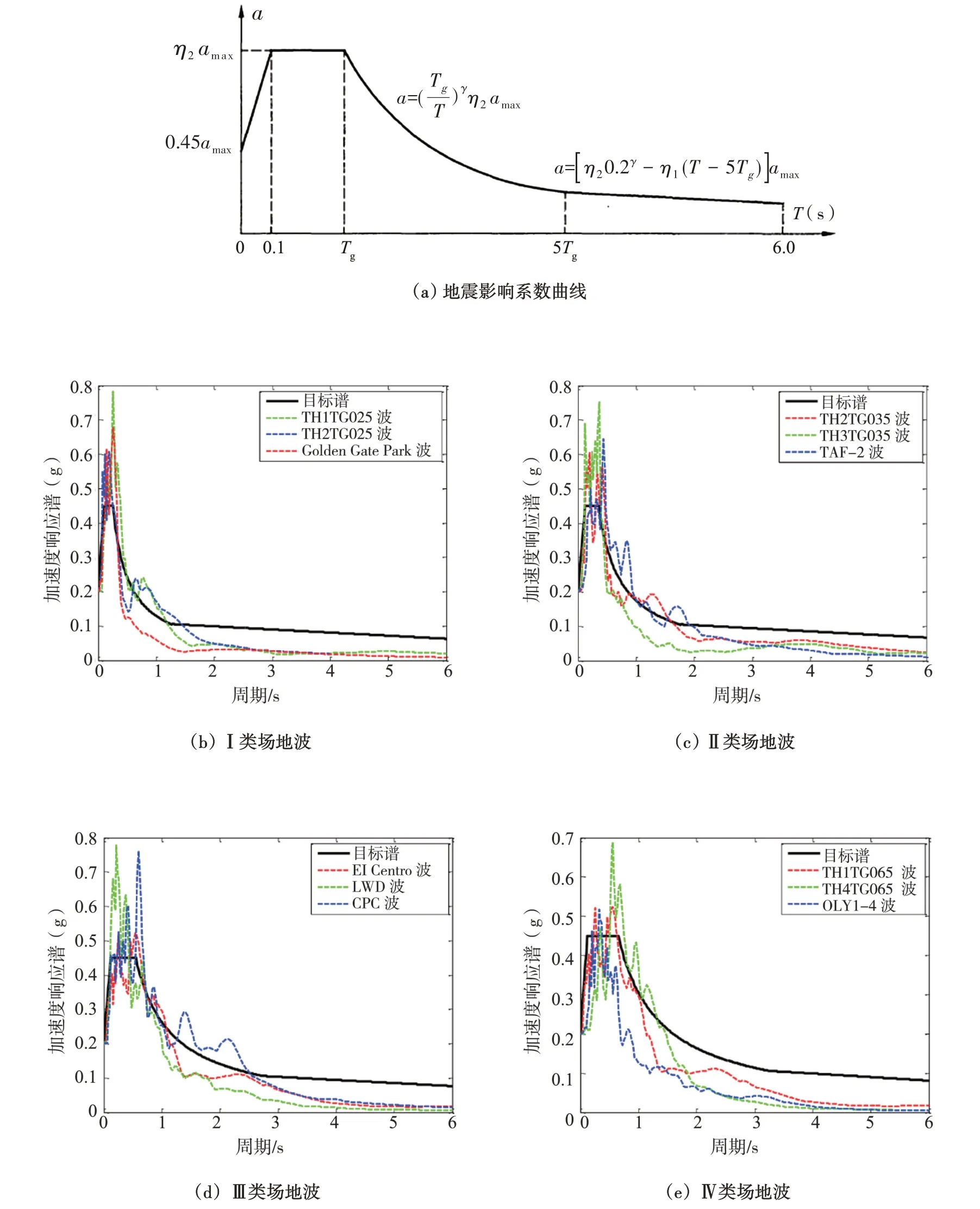
图5 地震动输入Fig.5 Ground motion input
3.2 数值分析
以上述地震波作为地震动输入,以作用于卧式储罐底部支承的基底剪力作为控制目标,对比分析不同地震动输入及不同场地条件下考虑储液晃动的两质点模型与规范单质点模型计算差异,研究储液量分别为H=1.5R填充、H=R填充时储液晃动对卧式储罐地震响应的影响,计算结果如表1~表8所示。若储液填充量为H=1.5R时,考虑储液晃动双质点模型参数,m c=1 270 kg,m r=3 830 kg,ω=4.98 rad/s;单质点模型参数m c=mc+m r=5 100 kg。若储液填充量为H=R时,考虑储液晃动双质点模型参数0.5,m c=1 423 kg,m r=2 152 kg,ω=4.21 rad/s;单质点模型参数m c=3 575 kg。
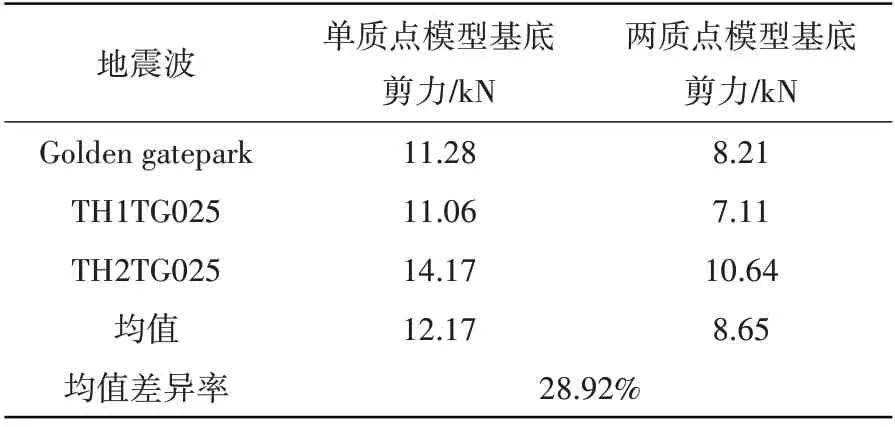
表1 Ⅰ类场地85%填充底部剪力峰值对比Table 1 Comparison of shear peak at 85%filling bottom of class I sit
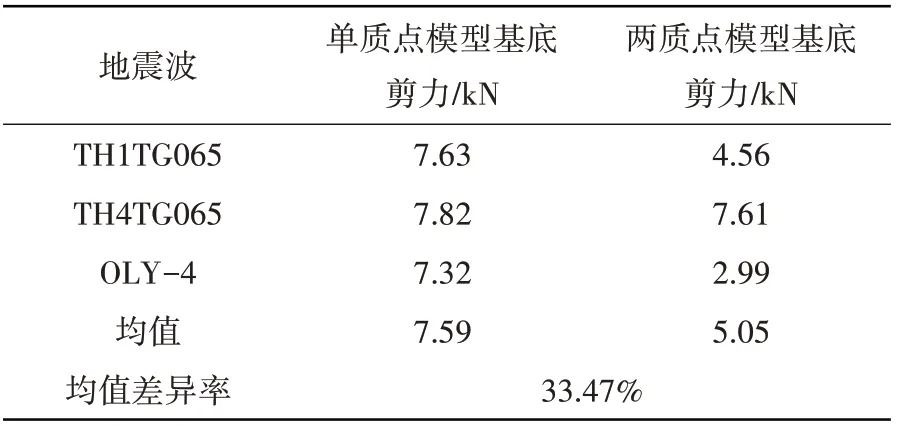
表8 Ⅳ类场地50%填充底部剪力峰值对比Table 8 Comparison of peak shear force at 50%filling bottom of class IV site
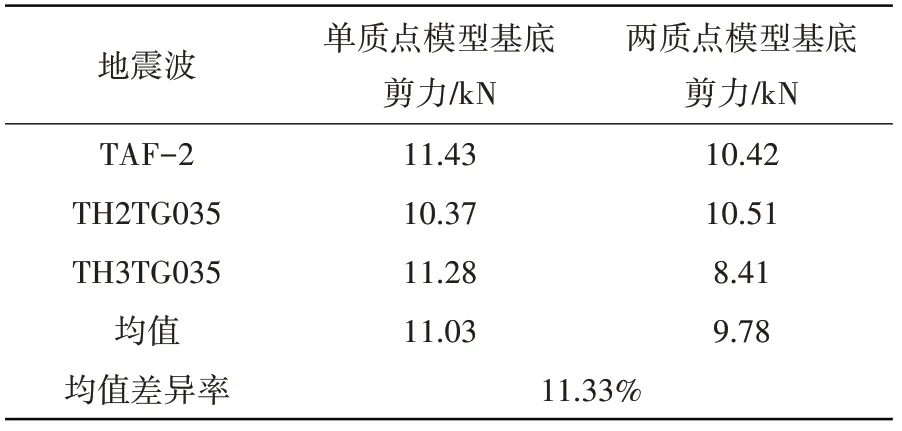
表2 Ⅱ类场地85%填充底部剪力峰值对比Table 2 Comparison of shear peak at 85%filling bottom of class II site
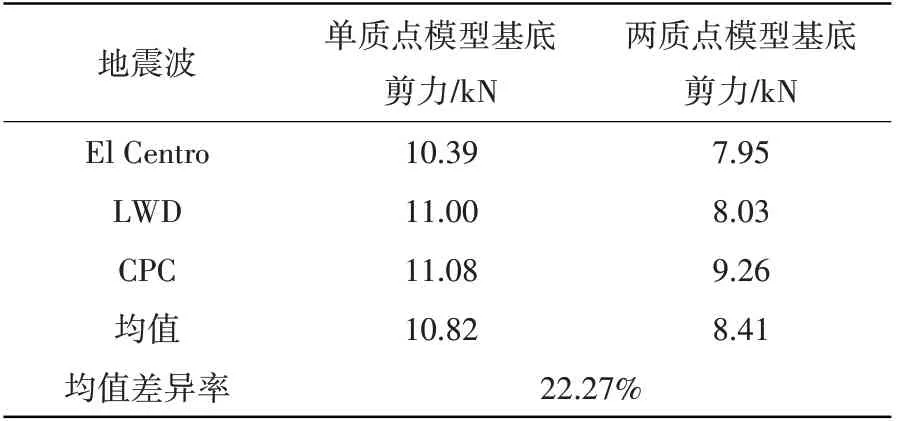
表3 Ⅲ类场地85%填充底部剪力峰值对比Table 3 Comparison of shear peak at 85%filling bottom of class III site
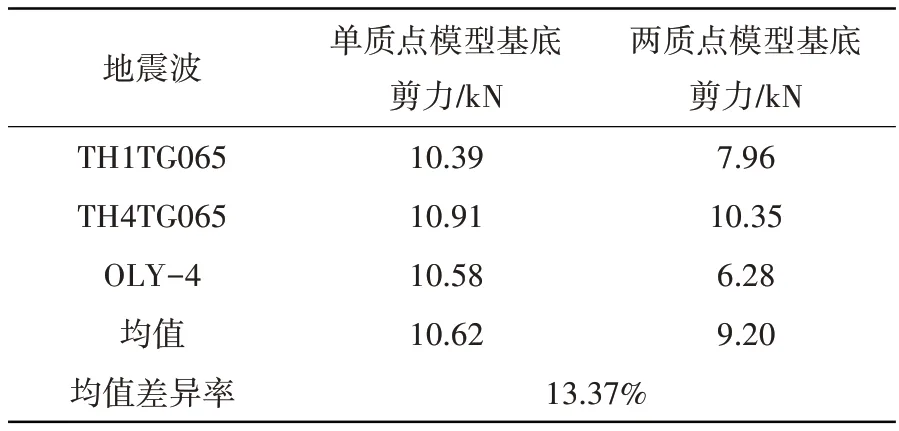
表4 Ⅳ类场地85%填充底部剪力峰值对比Table 4 Comparison of shear peak value of 85%filling bottom in class IV site
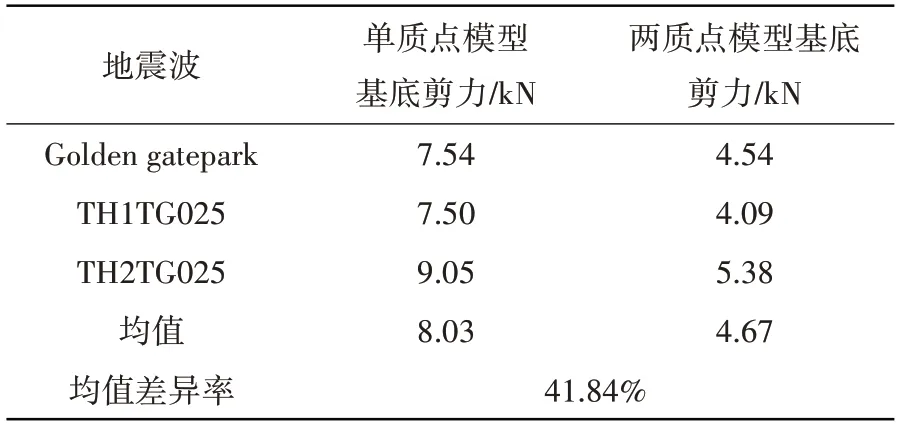
表5 Ⅰ类场地50%填充底部剪力峰值对比Table 5 Comparison of peak shear force at the bottom of 50%filling of class I site
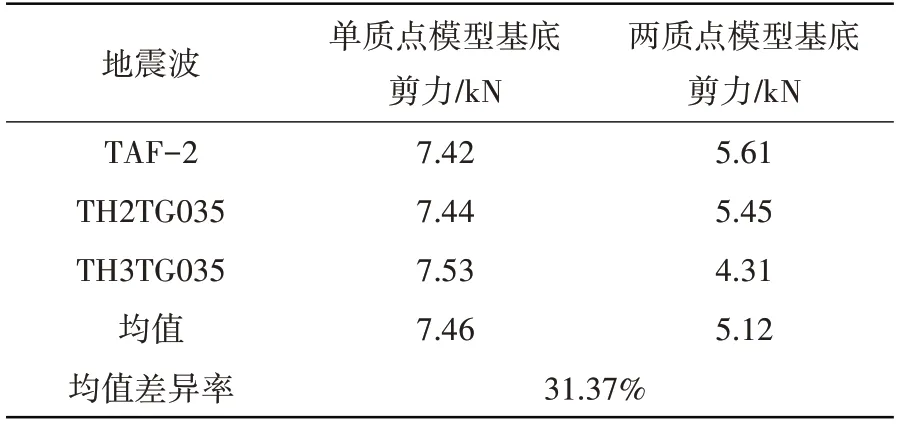
表6 Ⅱ类场地50%填充底部剪力峰值对比Table 6 Comparison of peak shear force at 50%filling bottom of class II site
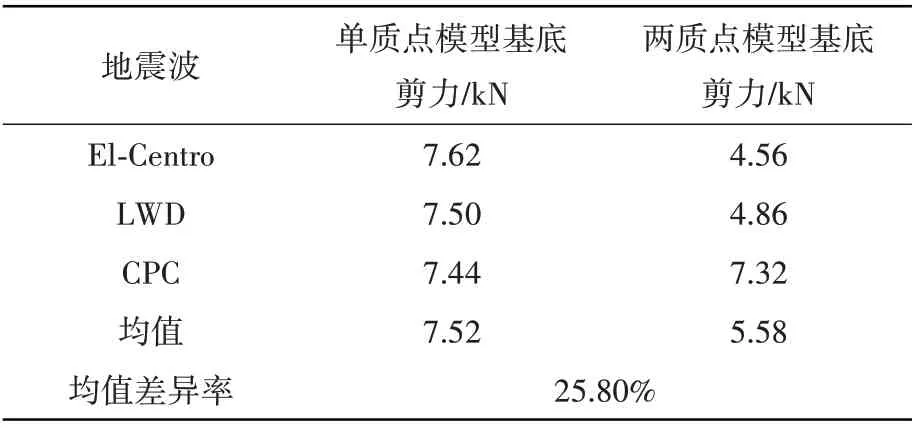
表7 Ⅲ类场地50%填充底部剪力峰值对比Table 7 Comparison of peak shear force at 50%filling bottom of class III site
表1~表8展示了4种场地波作用下储液量分别为H=1.5R及H=R时基底剪力的峰值。表中数据显示,单质点模型计算所得各类场地条件下基底剪力峰值均大于考两质点模型,差异率约为10%~40%,说明考虑储液晃动后对卧式储罐的地震响应有一定抑制作用。计算过程中可以发现储液量分别为H=1.5R及H=R时单质点模型基本自振频率为45.34 Hz、54.49 Hz,而考虑液体晃动的两质点模型的地震响应振型主要为液体晃动振型(0.79 Hz、0.67 Hz)和液固耦合振型(52.57 Hz、71.22 Hz)。由于储液晃动频率与主振型频率相差较大,可认为其互相不影响,因此两质点模型仅考虑液固耦合振型的影响。根据图5(a)中地震影响系数曲线可知,2种计算模型的自振周期均小于0.1,处于图中T=0~0.1的直线上升段,且单质点模型的计算自振周期均大于两质点模型,因此可知其动态系响应计算结果应大于考虑液体晃动的两质点模型。
4 振动台试验与理论模型对比
选取第3节中卧式储罐算例作为原型罐,以相同的几何尺寸(1:1)及材料加工制作振动试验模型罐,如图6所示。由于模型关于原型罐相同,根据相似原理输入的台面地震波无需进行缩放处理。选取El Centro波及Taft波作为地震动输入,PGA=0.2 g。储液高度为H=1.5R。

图6 卧式储罐振动台试验Fig.6 Shaking table test of horizontal storage tank
试验中采用位移传感器及三向动态应变片采集液体晃动及鞍座底部剪应变,如图7所示。其中D1为晃动波高测点,S1为鞍座底部应变测点。根据材料力学,理论分析时鞍座底部动态剪切应力可表示为:
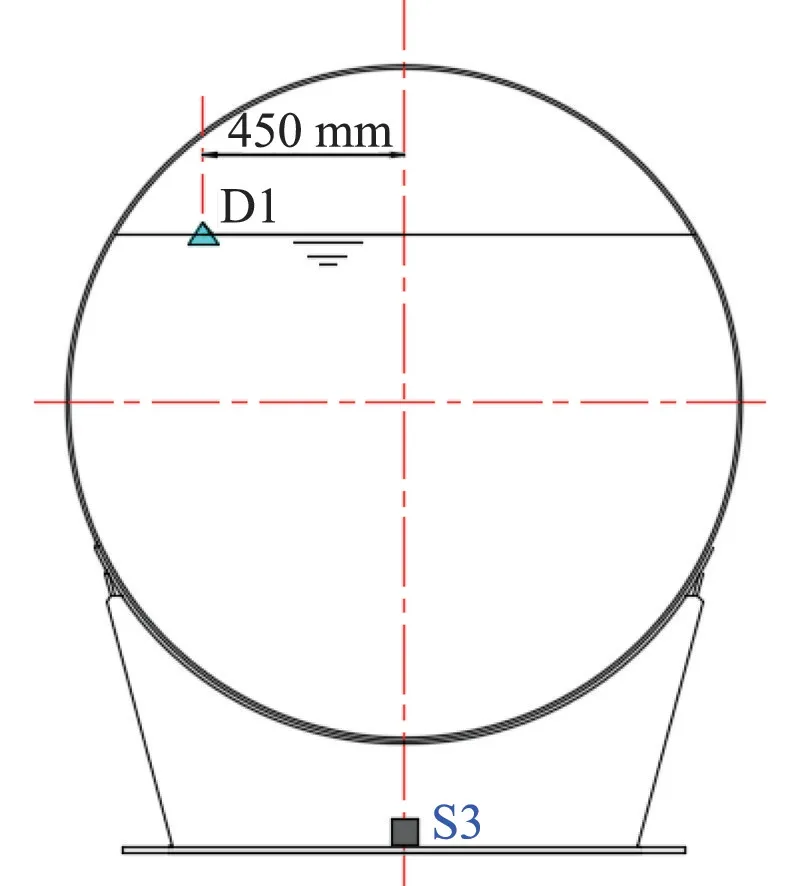
图7 数据采集测点Fig.7 Data acquisition measuring points

式中:Q为底部剪力;S y是横切线一侧的区域在剪切应力作用下相对于中性轴的静态力矩;I s是鞍座横截面的惯性矩;b是在所需剪切应力下的横截面宽度。
图8展示了El Centro波及Taft波作用下振动台试验与考虑液体晃动两质点模型理论计算所得液体晃动波高的时程曲线。从图中可以看出理论计算结果与试验结果较为吻合,实测液体晃动频率为0.778 5 Hz,而理论模型中液体晃动第一阶振型的晃动频率为0.79 Hz,两者基本一致,说明液体晃动主要以第一阶振型为主。表9、表10为晃动波高及鞍座底部剪切应变的峰值对比,从数据中可以看出两质点模型计算结果更接近试验数据,说明考虑液体晃动简化力学模型能更加接近真实地反应卧式储罐的地震响应。规范中单质点模型计算结果偏大,抗震设计更加保守。
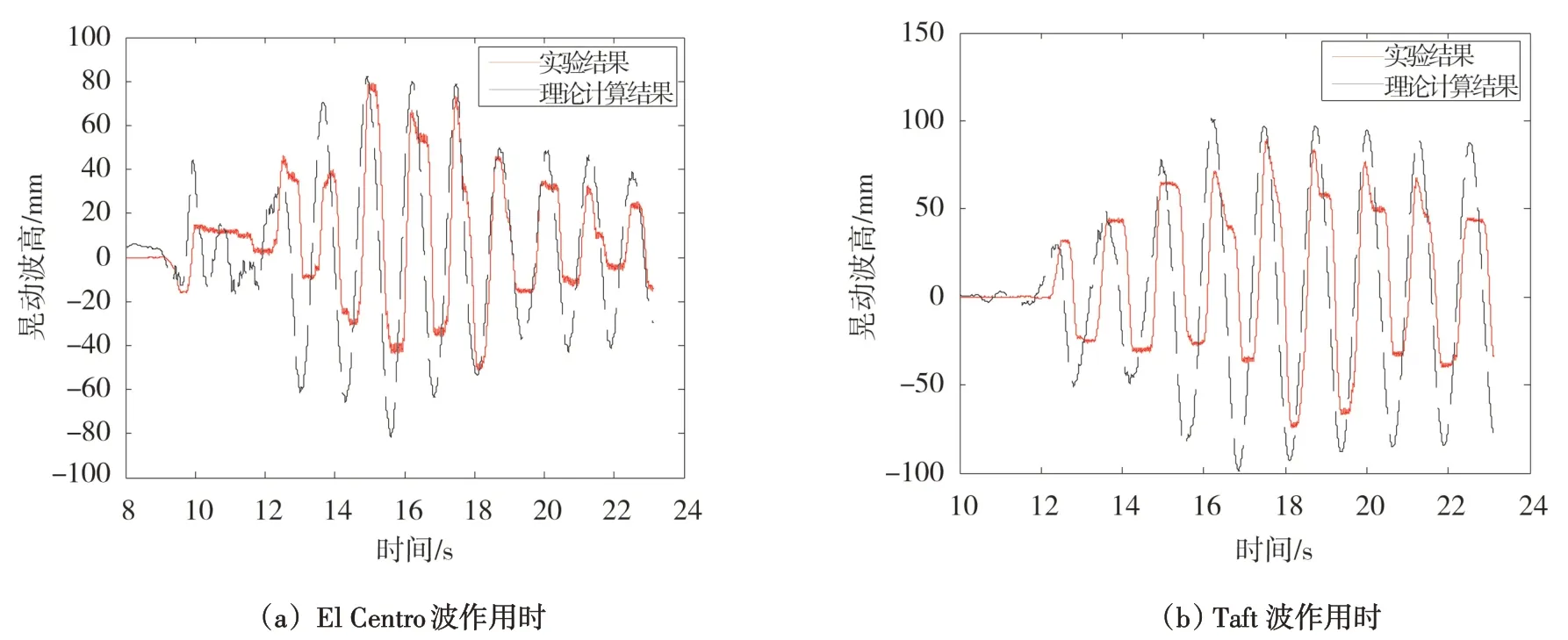
图8 晃动波高时程曲线对比Fig.8 Comparison of sloshing wave height time history curves

表9 晃动波高峰值对比分析Table 9 Comparative analysis of sloshing wave height and peak value
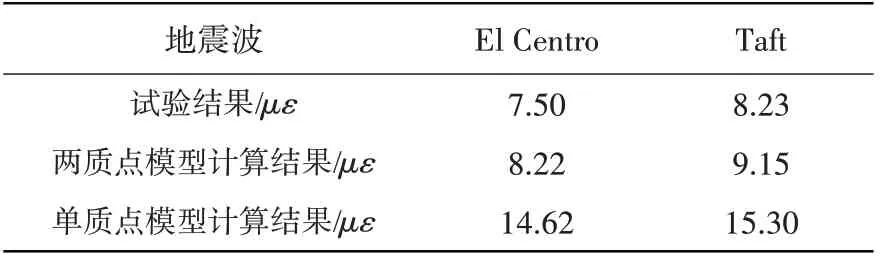
表10 鞍座底部剪应变峰值对比分析Table 10 Comparative analysis of peak shear strain at saddle bottom
5 结论
(1)基于卧式储罐考虑液体晃动的双质点简化力学模型,与规范中不考虑储液晃动的单质点计算模型进行地震响应对比分析。数值研究表明储液晃动对卧式储罐地震响应存在一定抑制作用,地震响应降低约10%~40%。
(2)两质点模型计算结果更接近试验数据。考虑液体晃动简化力学模型能更加接近真实地反应卧式储罐的地震响应。规范中单质点模型计算结果偏大,抗震设计更加保守。

