考虑场地-城市效应的复杂相互作用体系地震响应研究进展
王国波,巴 峰,王 垚,谢伟平
(1.温州大学建筑工程学院,浙江温州 325035;2.武汉理工大学土木工程与建筑学院,湖北武汉 430070)
引言
随着城市化进程加快,高层建筑密集出现,地下空间大规模利用,越来越多的复杂地下空间结构涌现(图1(a)[1]),结构之间的距离也越来越近(图1(b)[2])。在地震时,一方面地表结构在惯性力作用下发生剧烈晃动,结构基础如同一个震源,将地震动能量反射回地基土,从而影响场地土及邻近地下和地表结构的响应;另一方面,大型复杂地下结构的存在会改变地震波的传播路径,从而影响场地土和邻近地表结构的响应。因此,地下结构、土体和地表结构三者构成了一个复杂的相互作用体系,其中包含了土-地下结构[3]、土-地表结构[4]、地表结构-土-地表结构[5]、地下结构-土-地表结构[6]、地下结构-土-地下结构[7]、带地下室结构中地下室与地表结构[8]等诸多复杂的相互作用子体系。目前针对上述单个或多个子体系地震响应规律的研究成果相对较多,但将这诸多子体系综合在一起作为一个整体,研究其地震响应规律的研究成果并不多见。在城市高层建筑越来越密集、地下结构规模越来越大且结构越来越复杂、地下结构与地表高层建筑无缝衔接在一起的大背景下,极有必要开展针对场地-城市相互作用(Site City Interaction,SCI)复杂整体的地震响应规律的研究。本文对该领域的研究现状和成果进行归纳总结,希望能对该领域研究工作的开展起到一定的促进作用。

图1 典型大型复杂城市地下空间与密集地表结构效果图Fig.1 Typical large complex urban underground space and dense surface structure effect map
1 场地-城市效应的由来
地震学家很早便知道不能将地震测量仪器安装在树附近,以避免测量出现较大误差,这是由于地震时树的晃动会影响周围土体,从而影响测量仪器的工作,也即考虑到土-结构相互作用(Soil Structure Interaction,SSI)的影响[9,10]。Gueguen等[11]对位于European Volvi场地上的缩尺模型试验结果表明SSI效应对结构周边土体的运动以及结构自身响应有显著影响,因此,学者们自然而然地想到两个相邻的结构(地表结构或地下结构)之间也可能产生相互作用,即结构-土-结构相互作用(Structure Soil Structure Interaction,SSSI)[12]。由此可进一步推广:城市中存在着大量密集分布的建筑结构,地震时结构与结构、结构与土体之间也会产生显著的相互作用,即场地-城市相互作用(SCI),已有研究表明位于软土层上的建筑群会显著改变其周围地表的运动(Contamination of Ground Motion by Buildings,即CGMB现象)[13]。
从作用机理上分析,土-结构相互作用的过程可描述为:地震波经土体传播到结构处,导致结构发生振动,这种振动的部分能量反射回土体从而影响结构周边场地的地震响应。在此基础上,若存在两个结构,则将发生结构-土-结构相互作用,其过程可描述为:地震波经土体传播到两结构处,导致结构发生振动,振动的一部分能量反射回土体影响周围场地的地震响应,一部分能量经土体传递到相邻的结构上,从而影响临近结构的地震响应。而3个结构作为多SSI体系的最简单形式,其相互影响机理与结构-土-结构相互作用相似,仅结构数量更多。因此,可认为在特定条件下,3个结构即可产生所谓的场地-城市效应。
然而,在传统的地震学和地震工程应用中城市建筑物的存在通常被忽视,地面运动仅考虑震源和场地条件,认为结构在地面运动作用下的响应与周围结构无关,从而忽略了土-结构之间的多重相互作用,即将结构考虑为体系中的一个被动成分,这种近似在大多数场合是合理的,但对于拥有大量密集建筑物的大型城市则值得商榷。1985年墨西哥地震中出现的一些非典型地震响应及破坏特征,例如记录到了较长的持时及拍振现象(图2)[14]。其中拍振现象是指2个振幅不同、频率接近的简谐波形叠加时产生振动交替变化的现象(图2)。事实上,墨西哥城具有深厚的软粘土层,有利于土-结构相互作用,且建筑物的固有频率与盆地的固有频率十分接近,放大了能量的交换,导致显著的场地-城市相互作用。另外,1976年意大利地震(Friuli,Italy)的震害调查中发现了一个奇特的现象:连续相邻的建筑物表现出其中一幢建筑物完全倒塌而相邻建筑物几乎没有损伤的交替震害现象[15](图3),这种结构损坏模式无法通过传统的单独分析单一结构的方法进行解释,这与SCI效应密切相关。

图2 1985年墨西哥地震中记录到的长持时、拍振现象[14]Fig.2 The phenomena of long duration and beat vibration recorded in Mexico earthquake in 1985[14]

图3 连续相邻的建筑物表现出其中一幢建筑物完全倒塌而相邻建筑物几乎没有损伤的交替震害现象[15]Fig.3 Alternate earthquake damage of successive adjacent buildings during the 1976 Friuli earthquake,Italy[15]
区别于土-结构相互作用以及结构-土-结构相互作用的研究,场地-城市效应的研究对象往往具有数量更多的结构和更广的土体范围。因此文中拟基于已有研究成果,按地表结构分析模型、研究方法、影响因素、评价方法及指标等四个部分对场地-城市效应研究现状和进展分别进行归纳和总结。
2 地表结构分析模型
地表结构在SCI效应下的地震响应规律是关注的重点,因此合理的地表结构分析模型对反映结构在地震作用下的真实状态十分关键。而真实城市中存在数量庞大的不同种类结构,这些结构往往具有不同基础形式、高度、动力特性等,但受计算规模和计算效率的限制,有必要对结构模型进行适当的简化。
早期的地表结构模型大多采用质量-弹簧模型。Boutin等[16]建立了由集中质点、弹簧单元、阻尼器以及刚性浅基础构成的线弹性单自由度体系二维模型,分析表明SCI效应会导致响应持时的增加,响应幅值的扰动以及拍振现象的出现;Guéguen等[17]建立了类似3DOF的弹性二维模型,以考虑结构的摇摆运动,但忽略不同建筑物之间的相互作用,结果表明地表响应相比自由场响应减少10%;随着计算能力的提升,逐步将结构简化为具有均匀力学特性的均质弹性或粘弹性矩形块或长方体,其单元类型与土体相同,并通过修改块体的密度和弹性模量等参数使其具有与实际结构等效的力学性质[9,22]。将上述各类分析模型的特点和代表学者进行归纳,如表1所示。

表1 场地-城市效应研究中常用的几种结构简化模型及其特点Table 1 Several simplified structural models and their characteristics commonly used in the study of site-city effects
受1985年墨西哥大地震对墨西哥城影响的启示,对于软土地区的高层建筑群,在地震时高阶振型的影响不容忽视,但目前的简化分析模型大多无法考虑高阶振型的贡献,还需进一步完善。另外,现有研究大部分将结构简化为弹性模型,很少考虑结构的非线性以及精细化模型,而在实际地震作用下结构往往已经进入非线性状态,这可能使得结构群的整体振动频率发生变化,进而影响其地震响应。由于问题的复杂性,很难提出一种普遍适用的分析模型。因此,结构简化分析模型还需进一步提炼和完善,但最根本的还是针对具体问题采取合适的分析模型。
3 研究方法
3.1 理论分析
在理论分析方面,已有大量研究基于简化的理论模型,采用不同的方法考虑结构与土体、结构与结构之间相互作用,分析SCI效应对结构和土体响应的影响,并探讨相关的影响因素。
Xiong等[18-19]以四川大学望江校区为例,采用集中质量的简化分析模型探讨了SSCI效应(Soil-structure cluster interaction),结果表明相邻结构(群)可显著改变结构的地震震害,进一步拓展了场地-城市相互作用的研究范畴。Boutin等[16]基于城市是由简单振子周期性分布的假设,从宏观的角度提出了评估城市的存在对地震运动影响的2种分析方法,分析得出:与自由场相比,SCI效应会导致响应持时的增加,响应幅值的扰动以及拍振现象的出现。Lu等[20]提出了分别用于模拟低层结构和高层结构的非线性多自由度剪切模型和弯剪模型,并对其合理性进行了验证。Chergu等[21]通过对多个带有刚性基础的单自由度体系的模型在二维反平面振动作用下的响应进行分析,提出通过第一特征函数的形状来描述地震作用下结构集体行为的观点,发现城市的主频并不取决于组成城市的建筑数量,而取决于建筑自身特性。Uenishi等[15]通过对1976年意大利Friuli地震的建筑破坏模式的分析,认为可通过建筑破坏模式反演确定输入地震动的特性。Wirgin等[22]对无限分布的周期性城市模型的地震响应进行分析,采用基于空间-频域的模式匹配法得到其理论解,通过与基于空间-时域的有限单元法得到的数值解对比发现:2种方法在建筑数量为10的情况下结果基本相同,且大量建筑的存在会影响地面的地震响应。Lombaert等[23]通过非平稳Bethe-Salpeter方程的近似解估计城市的存在对地震持时的影响,结果表明:建筑群的惯性效应导致场地一阶频率降低,且城市的存在会增强场地响应的空间变化性。Guéguen等[17]采用格林函数法求解由于建筑振动产生的波场,将不同建筑对参考点的影响视作单个建筑影响的叠加,忽略不同建筑之间的相互作用,结果表明地表响应相比无建筑存在的自由场响应减少10%。Lombaert等[24]还通过随机分布在分层弹性半空间上的振动散射体模型来研究波的多重散射效应,证明地震激励下建筑群中存在波的多重散射效应,在地震波低频范围,
建筑的存在会导致场地响应的均匀改变;在地震波的高频范围,由于建筑振动产生的散射波对场地地震响应的影响,均方根响应明显大于平均响应。
3.2 数值模拟
目前在涉及到场地和结构的相互作用研究中最常用的数值方法主要有:有限差分法(FDM)、有限单元法(FEM)、边界单元法(BEM)以及谱单元法(SEM)。这些方法在SCI效应研究中的特点以及应用各方法开展相关研究的代表学者如表2所示。

表2 场地-城市效应数值模拟中常用的几种方法的对比Table 2 Comparison of numerical methods commonly used in the study of site-city effect
3.2.1 有限差分法
Kumar等[25,26]采用有限差分法,对2D和3D模型的场地-城市效应进行研究,发现2D和3D结构模型的基频与同样的1D模型基频相比分别降低35.6%和10.8%,且近距离分布的结构在SV波作用下的谱放大系数大于SH波作用下的谱放大系数。与单个结构存在的情况相比,SCI效应导致在结构基频处谱放大系数的减小以及基频带宽的分裂现象。Kumar等[27]还对2D矩形和椭圆形盆地的基频和SCI效应进行研究,发现盆地基频随形状比增加而增大。当形状比大于0.25时,盆地2D基频大于1D基频。当其他参数一致时,椭圆形盆地基频大于矩形盆地,对SCI效应的研究发现当城市和盆地共振时,结构响应减小。Sahar等[28-29]采用粘弹性有限差分模型,对3D盆地上城市的存在对地面运动的影响进行量化评估,结果表明盆地形状、土体性质、城市布局、建筑类型和城市密度对SCI效应有重要影响,且在建筑-盆地体系的基本频率与场地以及输入地震动的主频相近时,SCI效应会使城市内部响应显著减小,与建筑高度相比,城市密度对SCI效应的影响更大,而不同建筑的存在可能导致建筑响应的相干性降低。
3.2.2 有限单元法
由于有限单元法存在计算大型3D模型时间成本较高的问题,因此对计算方法进行优化十分重要,Bielak等[30]和Yoshimura等[31]针对地震模拟过程中因区域规模较大和重复计算而导致计算效率低的问题,开发了基于有限单元的域缩减法(Domain Reduction Method,DRM),经验证,该方法可以显著提高大尺度地震模拟的计算效率。Isbiliroglu等[32,33]对地震作用下单个建筑以及理想建筑群与土体的相互作用效应进行研究,建立相应的三维有限元模型,并结合域缩减法模拟地震激励,结果表明SCI效应与建筑的数量、动力特性、间距以及相对于土体的阻抗有关,该效应的影响表现为地表运动空间变化性增加,在建筑-基础体系自然频率以上的频率区段,建筑基础的运动显著减小。Taborda等[34]采用可考虑土体非线性的大尺度模型地震分析软件Hercules对3D城市模型的研究表明:结构的存在会明显改变城市中的地面运动,土体非线性会引起地面响应的减小,以及高频响应成分的出现,SCI效应会对城市内部以及城市周边的地震响应产生显著影响,其影响范围为建筑周围300m到500m,还会显著影响地面运动的空间变化性。另外,结构响应的幅值与不考虑城市效应相比有所衰减,而结构之间的地面运动响应有所放大,在建筑周围100m范围内最为明显。Taborda等[35]还对考虑土体非线性的三维异质盆地上的城市模型进行研究,探讨了土体非线性和SCI效应对地面运动以及建筑自身运动的影响。结果表明土体的非线性行为会导致衰减效应以及地面响应的空间变异性增强和明显的三维盆地效应,而建筑群的存在会显著改变近场地面运动和建筑自身运动。
在规律研究方面,Groby等[36]对位于耗散介质构成的场地上的城市模型的地震响应进行模拟,结果表明结构内部以及地表的响应表现出很强的空间变化性以及持时的增加。但真实城市的分布范围较广,场地环境空间变化性强,这种简化具有一定的局限性,有必要考虑非均质土体对SCI效应的影响。Tsogka等[37]研究二维城市模型的地震响应,得到了与Boutin等[16]相类似的结果,且结构的响应并不是系统性地增加,因此在地震作用下,会出现不同的破坏状况,而软土会导致城市在地震作用下的脆弱性更加显著。Varone等[38]采用考虑吸收层的有限单元法,对位于真实土层分布条件下的二维有限元模型进行了研究,发现建筑的存在会导致建筑基础底部响应的显著减小以及建筑周边横向区域能量的重分布。Wirgin等[39]通过位于弹性半空间上的周期性分布的二维城市模型在垂直入射SH波的作用下对地面运动的持时和幅值的影响进行研究,发现SSI效应会导致结构响应主频的减小,幅值略微增大,随着建筑高度的增加,对地面运动和建筑运动的影响越大,位于软土层上的高层建筑产生显著的SSI效应,导致地面响应持时和幅值的增加以及拍振现象的出现。
3.2.3 边界单元法
Clouteau等[40]提出了一种用于求解分层弹性半空间上的三维城市模型响应的数值方法,该方法基于边界单元和建筑物的模态表示的变分耦合。将其应用于周期性城市和非周期性城市的地震响应分析,结果表明:入射波场的改变主要发生在软土层中,对于周期性城市,建筑的响应幅值未明显改变,但频域响应的峰值分裂成两个,导致时域中拍振的现象;而在非周期性城市中,建筑间的相互作用的影响随着频率的增加而增大。Semblat等[41]以Nice城为背景,考虑土体的横向异质性,采用边界单元法对位于其上的周期性城市,非周期性城市以及真实城市的2D模型进行对比分析,结果表明SCI效应对城市附近空地的地震灾害有较大影响,对城市的部分区域是有利的,对另外一些区域是不利的(特别是在城市边界处)。这些影响与城市的布局、异质性以及密度等密切相关。随后,Semblat等[42]还基于类似模型和方法对不同建筑密度和建筑频率下的地表运动相对于自由场的放大系数进行研究,结果表明当建筑结构的固有频率与表层土的自然频率一致时,SCI效应会显著增大地表运动的放大系数。通过对单层均质土上的城市模型和考虑横向异质性盆地上的城市模型进行数值分析,研究了不同建筑分布,建筑密度和类型对SCI效应的影响,结果表明场地的横向异质性对城市振动产生的波场有重要影响。
3.2.4 谱单元法
在利用谱单元法模拟地震波传播过程方面,Mazzieri等[43]基于谱单元法开发了一种开源程序SPEED(SPectral Elements in Elastodynamics with Discontinuous Galerkin),可在局部或区域尺度上模拟三维异质粘弹性媒介中的地震波传播,网格划分时可改变局部网格尺寸。部分学者基于该开源程序对SCI效应进行研究,Guidotti等[44]采用SPEED软件建立了60 km×60 km×20.5 km的场地模型和位于其上的1 km×1 km×0.0 5km的真实城市模型(如图4所示),研究结果表明SCI效应使得城市内部的地面响应相比于自由场差异超过1/3,建筑振动会使运动的空间变化性增大,行波效应所导致的建筑振动相位差异会增大近距易碰撞建筑的破坏。Kato等[45]以香港九龙地铁站及周边地表建筑为背景,建立了只考虑地表结构-基础以及同时考虑地表结构-基础和地铁站的3D模型,采用SPEED软件进行地震分析,结果表明考虑地下车站与不考虑相比,会导致地铁站上方土体的放大效应减小,虽然该案例中结构和场地的自然频率有很大不同,但SCI效应依然明显,说明完整真实的城市布局对其地震分析是十分重要的。Lu等[46]提出了考虑SCI效应的区域范围建筑非线性时程分析的数值耦合方法(如图5所示)。该方法基于MDOF建筑模型并采用SPEED软件模拟波的传播过程。通过对振动台试验的模拟验证了该方法的可靠性,采用该方法对位于盆地上的城市模型进行研究,发现SCI效应整体上会降低建筑的动力响应,但也会使部分建筑的响应增大,这与具体地震动,场地及建筑布置相关。Guéguen等[47]通过对位于Grenoble,France的三座邻近相同建筑物的宏观地震强度差异的分析,结合谱单元法模拟,认为群体效应导致这一现象,建筑群中建筑物地震响应的变化取决于震源相对于建筑群的方位角,群体效应还会导致共振频率的分裂,振动幅度的减小,并对城市效应产生影响。

图4 无网格法的网格划分示意图:在不同区域采用不同尺寸的网格[44]。Fig.4 Sketch of the non-conforming meshing strategy:different mesh sizes are adopted within different sub-domains[44]

图5 场地-城市效应的数值耦合方法[46]Fig.5 Numerical coupling scheme for SCI effects[46]
3.3 试验研究
在SCI效应的试验研究方面,主要采用的方法为振动台试验。由于SCI效应所涉及的城市模型较为复杂,因此相关的试验研究相对较少。
现有试验研究主要是针对2个或3个结构的结构-土-结构相互作用的研究,而建立不同结构类型(不同地表建筑结构和地下结构)和大量(5个及以上)建筑结构分布的模型进行振动台试验的较少。Boutin等[48]和Schwan等[49]以一个最多考虑37个各向异性结构的理想城市模型为研究对象(图6),对比分析该模型由振动台试验得到的实际解、基于等效城市阻抗模型得到的理论解以及由边界单元构成的数值模型得到的数值解。发现SCI效应使自由场原主频处响应明显减小,响应主频向两侧移动,导致时程曲线出现拍振的现象以及波场相干性降低。熊峰等[50]用混凝土单柱加质量块简化模拟地表结构,进行了单一和五个地表结构群的对比振动台试验,结果表明:在地震作用下高层建筑群内结构存在明显的相互作用,相邻建筑的存在会使上部结构频率降低,而上部结构加速度和位移反应的变化取决于输入地震波的频谱特性。作者课题组等[51]采用多台阵振动台试验进行了1个、3个和5个地表结构地震响应试验研究(图7),其中还考虑了建筑不同净间距的影响,结果表明建筑物间距和数量对场地土和结构自身地震响应的影响十分显著。Aldaikh等[52]通过振动台试验对2个或3个建筑模型之间的相互作用进行研究,发现与单个建筑模型相比,一个或两个相邻建筑物的存在会导致建筑的地震能量以及峰值加速度响应增大或减小,与建筑的高度有关。
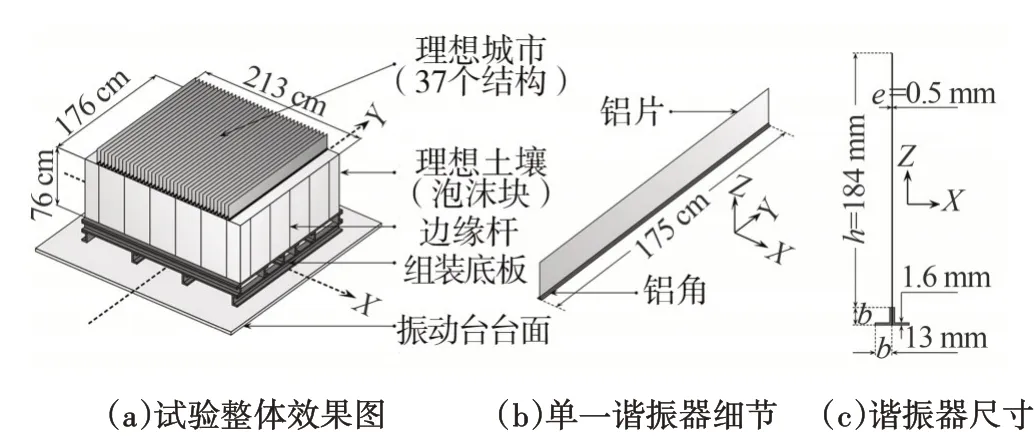
图6 采用铝片模拟结构群的场地-城市效应振动台试验[49]Fig.6 Shaking table test of site-city effect using aluminum sheet to simulate structure group[49]

图7 3个和5个结构存在时的场地-城市效应振动台试验[51]Fig.7 Shaking table test of site-city effect with 3 and 5 structures[51]
4 影响因素
影响SCI效应的因素众多,基于已有文献可概括出以下5个主要影响因素:城市密度、结构分布形式、结构基础形式、土-结构频率比、场地条件。下面分别对这5个影响因素进行简单的总结,并指出目前存在的不足。
4.1 城市密度
结构之间的间距一定程度上决定了它们之间相互作用程度的强弱,这在结构-土-结构相互作用的研究中已经得到证明[12]。已有大量学者对城市密度的影响进行了研究并得到了一致的结论:在其他条件相同情况下,城市密度越大,SCI效应就越显著。因而在城市建筑群中结构分布越密集,它们之间的相互作用也就越明显。已有研究大多将城市密度定义为建筑总面积与城市区域总面积之比,对于二维模型则是建筑总宽度与城市宽度之比,显然与建筑物的数量以及间距相关。但该方法忽略了建筑分布形式的影响,显然具有一定的不合理性。已有部分研究表明结构的分布形式(即城市布局)对SCI效应有重要影响,参见4.2节。
4.2 结构分布形式
由于城市结构布局较为复杂,为了方便城市模型的构建以及进行参数分析,学者们首先从最简单的城市模型入手,将城市简化为等间距分布的相同结构,即周期性城市(如图8(a)所示),进而考虑不同结构类型和分布形式,建立更贴近实际城市模型的非周期性城市(如图8(b)所示)。
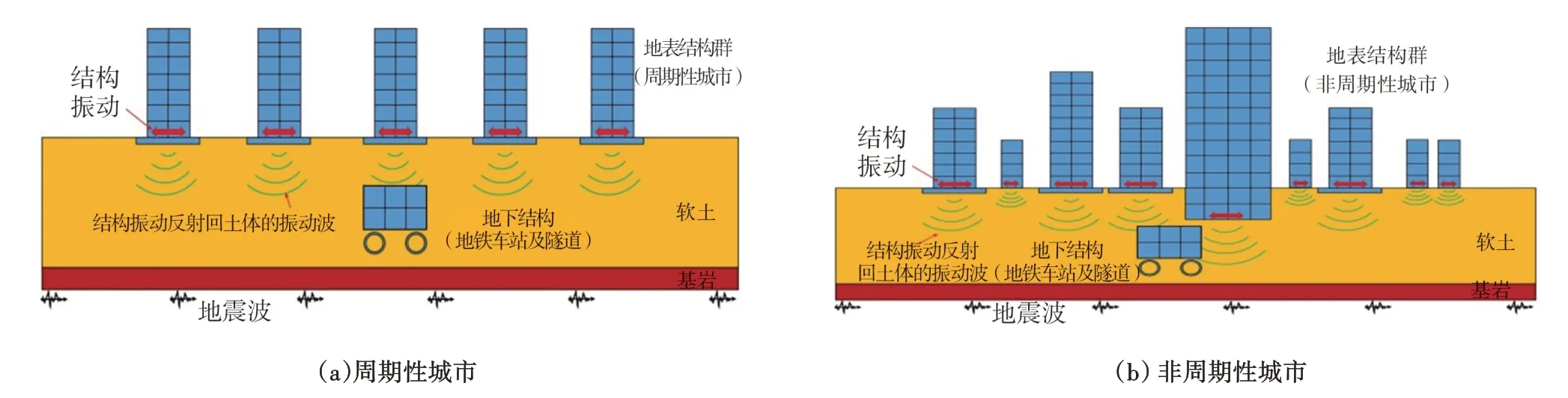
图8 周期性城市和非周期性城市示意图Fig.8 Schematic diagram of periodic and non-periodic cities
目前对均质土体上的周期性城市的研究较多[16,21-23,37,39]。在非周期性城市的研究方面,已有考虑不同结构类型、不等间距分布、结构方向性和扭转效应的SCI效应的研究,结果表明结构的分布形式对SCI效应的作用效果有显著影响。Isbiliroglu[33]等发现在扭转效应与SCI效应的共同作用下,结构响应在高频处略微增大。Bard等[9]指出在其他条件相同时,周期性城市内部的平均响应减少量最多达到50%,而非周期性城市中的减少量则不超过15%。因此,非周期性城市可能导致SCI效应的减弱。为了考虑结构分布形式的影响,Pinzón等[53]针对区域内具有相似建筑材料,结构形式以及几何形状的建筑群在地震作用下一栋建筑倒塌,而其他建筑只是轻微受损或无损坏的独特现象进行了研究,得出了方向性效应导致这种现象出现的结论,将考虑方向性的反应谱与已有规范反应谱进行对比,结果表明仍有部分响应超过规范值,因此在建筑抗震设计和研究的过程中,应该对方向性效应予以考虑。
在跨领域研究方面,Brulé等[54]将城市分布形式类比于超材料的结构形式,使用转换光学的技术,并通过数值实验验证建筑群可视作一组纯弹性,与入射地震波相互作用的共振器,这为SCI效应的研究以及未来城市规划提供了新的思路与方法。
后续研究应该对较为典型的建筑群布局如方形、环形分布等,以及不同类型建筑(中高层建筑和低层建筑)组合分布情况下的地震响应进行对比研究,得到最有利于建筑抗震的分布形式,这将从更为宏观的角度丰富抗震概念设计的内容,并为区域城市规划提供参考。
4.3 结构基础形式
已有研究大多基于刚性浅基础的假设,为了研究不同基础形式对SCI效应的影响,Chen等[55]对由相同带有桩基础的高层建筑构成的三维城市模型进行研究,发现结构群的存在减轻了单一结构-土相互作用的结构响应,并导致明显的地震动空间变化性。相邻结构可表现出完全交替的力学行为,且城市边缘的建筑物比城市中心建筑物受到更强烈的震动。SCI效应会使得城市区域内的地面运动减小,结构群对地面运动的影响距离与城市宽度相关,土体性质可显著影响体系的响应,甚至可以完全改变趋势。Clouteau等[56]探讨了基础特性对结构-土-结构相互作用效应的影响,研究发现采用浅基础时,相邻结构的存在对体系地震响应的影响较小,但对于嵌入基础,相邻结构的存在显著影响体系的地震响应,如增大结构顶部的振幅。
4.4 土-结构频率比
已有研究表明:当表层土基频与结构基频一致时,土和结构会发生明显的共振现象,导致结构振动出现显著的放大现象,进而将更多的能量辐射到土体中,展现出更为显著的土-结构相互作用以及结构-土-结构相互作用。已有研究对包括结构动力特性(高度,结构的纵横比,结构类型等),土的性质(土层厚度等),土-结构剪切波速比,刚度比等因素进行讨论,从本质上来说都是对土-结构频率比下SCI效应研究。普遍认为,表层土基频,而不是整个土层的基频,与结构基频越接近,SCI效应越明显。
但是,Uenishi等[15]、Chergu等[21]、Lombaert等[23]、Kumar等[26]、Wirgin等[39]发现SCI效应会导致结构群的固有频率比其中单个结构的固有频率有所降低,且由于城市的惯性效应,会使得场地的固有频率也会降低。因此在实际情况下,场地和建筑结构群的固有频率均不同于其单独存在时的固有频率。另外,在非周期性城市中,往往存在不同自振频率的建筑结构,如何确定整体体系频率是一个值得深入的关键问题。类似地,在非均质土体条件下,如何确定体系的固有频率也有待进一步探讨。
4.5 场地条件及地震波特性
场地的变化对地震波的传播有显著影响,研究表明非均质场地条件下城市中地震波的相干性相比于均质场地条件下更弱[54],另外盆地中可能困住由建筑振动传到土体中的振动波,这些波在盆地内部不断反射和散射,可能导致地面运动的放大,因此场地条件的变化首先会直接引起场地效应的变化,进而改变SCI效应。Kham等[57]采用边界单元法对位于盆地上的同质,周期性城市以及异质,非周期性城市的二维数值模型进行参数分析,结果表明当建筑的自然频率与场地的固有频率相同时SCI效应最为显著,导致建筑和地面的响应显著减小,城市内地面运动的空间相干性减小。Semblat等[41,42]以Nice城为背景,考虑土体的横向异质性,对位于其上的周期性城市,非周期性城市以及真实城市的2D模型进行对比分析,结果表明场地的横向异质性对城市振动产生的波场有重要影响。因此,土体的盆地效应[13]、分层效应和横向异质性[59]等场地条件的影响不可忽略。贺晨蕊等[60]采用有限元模拟方法建立了建筑群-沉积谷地二维模型,在频域与时域中对比分析此体系和单独沉积谷地的地震反应,结果表明:入射波频率较低时,由于共振效应的存在,在部分区域处建筑群-沉积谷地体系的地表位移响应幅值会大于单独沉积谷地,但随着入射波频率的增加,建筑群的存在又会对地震反应产生明显的减弱效果,因此输入波的特性对SCI效应的作用效果有显著影响。
5 评价方法及对应的评价指标
由于相关的量化方法众多,下面只列举较为常用的处理方法,给出其评价的具体方法及采取的评价指标,并以部分学者为代表阐述了其在对应方面所做的工作。
(1)地面扰动法
SCI效应最直接的体现是对场地土响应的影响,因此较早的评价方法是对比分析自由场地表以及考虑SCI效应时地表响应之间的差异,以定量描述SCI效应的影响范围和程度。显然,该方法采用地表加速度响应作为评价内容,具体采用公式(1)确定的地表扰动系数作为评价指标。

其中:μ为地表扰动系数,u SCI是考虑SCI效应时地表响应,uf f是自由场时对应位置地表响应。
地表扰动系数法便于操作,被大量用于评估场地受到的SCI效应影响程度大小(Kato等[45]、Isbiliroglu等[32,33]、Taborda等[34]、Chen等[55]、Kham等[57])。但Kham等[57]认为在运动效应和惯性效应的作用下,由基础辐射的波场在土层中传播,由于涉及到复杂的建筑环境,因此各个建筑产生的波场之间可能产生多种相互作用,并显著改变地表运动的模式。因此在地表扰动系数法的基础上通过分析地面运动的空间相关性,先定义协方差系数(式(2)),并在此基础上定义空间相干性长度Lu(式(3))作为评价指标:

其中:r为两点之间的距离,ω为频率,u是位移,*表示共轭转置。
该方法可对频域中城市内部响应的空间相干性进行评价,但由于处理方法较为复杂,理论性较强,导致该评价方法的应用受到一定的限制。
(2)结构响应扰动法
该方法与上述第一种方法相呼应,采用地表结构中某一个结构在单独存在和考虑SCI效应时的响应差异作为评价指标。一般将考虑SCI效应的城市中心的结构CB(Control Building)的响应与ICB(Isolated Control Building,即只有场地中心存在一个建筑结构的情况)的响应进行对比[32-33],如式(4)所示:

其中:η为结构加速度变化系数,aCB和aICB分别表示考虑SCI效应和不考虑SCI效应时对应结构的加速度幅值。
同样地,该方法也具有操作简单的有点,也是目前常用的评价方法之一。但这些以地表或结构响应峰值确定的评价指标过于简单,不能考虑地震动的全过程,因而所得到的结果还有待进一步检验。
(3)能量变化法
针对采用峰值响应代表测点的响应往往易忽略非峰值响应影响的问题,考虑到地震动能量是衡量地震等级的重要因素以及能量方法的优点,相关学者尝试从能量的角度提出评价方法及对应的评价指标。一般采用一定时间内速度v(x,t)的平方积分代表该时间段内的能量大小[9,13],如式(5)所示:

然后参照上述2种方法,以能量的变化作为评价指标[17,41,45,55],如式(6)所示:

其中:κ为能量变化系数,E SC I和EN O-SCI分别表示考虑和不考虑SCI效应时目标点的能量值。
相对于基于响应峰值的评价方法,能量系数法基于动能的表达式,能够考虑测点响应的全过程。但该方法将SCI效应笼统的用ESCI表示,无法综合体现结构特性、场地土特征等关键因素的影响。Boutin等[16]则在能量变化系数法的基础上,综合考虑地表结构群分布密集程度(建筑密度)、结构与土体刚度相对比等主要因素,提出结构-土能量比σ0作为评价指标(式7):

其中:Sb/S为建筑密度,βb/βs为结构与土体剪切波速之比(代表了土-结构刚度比),ρb/ρs为结构密度与土体密度之比。
Boutin等[16]认为SCI效应的影响随σ0的增大而增大,但σ0越大,产生的持时增加的效果越弱,当结构基频与场地固有频率一致时,SCI效应的影响最大。
Bard等[9]结合二维和三维城市模型的部分研究成果,采用结构高度和结构频率与表层土厚度与频率的比值以考虑土-结构刚度比的影响,提出了类似于式(7)的结构-土能量比评价指标,如式(8)所示:

其中:Sb/S为建筑密度,hb/hs为结构高度和表层土厚度之比,fb/fs为表层土体固有频率与结构基频之比。分析表明当该比值小于0.01时,SCI效应基本可以忽略,反之,应该考虑SCI效应对地表和建筑物地震响应的影响。
类似地,Guéguen等[17]基于3DOF结构模型和已有的阻抗函数对墨西哥城在实际地震作用下的响应进行求解,采用叠加原理考虑了建筑群内每个单一结构的贡献,重现了地震响应的长持时和拍振的现象。研究结果表明SCI效应主要取决于建筑密集程度、土层厚度与结构高度比以及土-结构刚度比,综合该3个因素提出SCI效应评估的量化公式(式9)。

其中:h bi/Hs是第i个结构高度与土层厚度之比,fs/fbi为土层基频与第i个结构基频之比,其他符号意义同上。
相比于公式(8),公式(9)认为土层总厚度,而不是公式(8)中的表层土厚度更值得考虑。但公式(7)-公式(9)都较为简洁,虽然在形式上有一定的差异,但均涉及相同的参数项,即城市密度、结构基频与土体基频之比、结构高度与土层总厚度或表层土厚度之比,一定程度上能够反应影响SCI效应的主要参数。
基于能量变化的评价方法及其相应的评价指标,考虑了单体结构的叠加影响、结构群的分布密集程度、土-结构刚度比等关键因素,是目前考虑因素最全面、使用也较为简单的方法,得到了广泛的使用。
上述公式仅适用于分布在均质土体上具有相同建筑类型的结构组成的城市,公式(9)虽可以考虑不同建筑类型的影响,但将各个结构的影响简单相加只满足于线性体系,随着研究的深入,这些公式可能会被细化以考虑一些更复杂的因素,例如土体非线性、场地条件的空间变化以及结构类型和分布形式的变化。
(4)传递函数(transfer function)法
传递函数定义为某一响应经傅里叶变换后的幅值与自由场对应处响应经傅里叶变换后的幅值之比随频率变化的函数。该方法与上述地面扰动的评价方法类似,只不过是在频率内进行,通过在频域中对比分析不同工况下的同一测点的响应,可以得到对响应变化影响最大的频率。另外可以通过在某一地震作用下的传递函数推断出在该特定场地-城市条件下,受到具有类似震源性质的地震作用下的SCI效应的影响,被广泛应用于SCI效应的频域分析中(Isbiliroglu等[32,33]、Kham等[57]、Semblat等[41]、Schwan等[49]、Guéguen等[17])。
(5)波场变化法
Isbiliroglu等[32]、Kham等[57]、Semblat等[41]、Yoshimura等[31]通过将不同位置的响应时程曲线绘制在同一图中,可以观察不同位置地震波场的差异,进而得到波场的空间变化趋势,该方法从宏观角度直观地反映波场的变化,同时可以对比不同工况下的波场差异,观察SCI效应可能引起的持续时间的增加以及拍振的现象,但由于曲线数量较多,往往只能显示出每条时程曲线的大致轮廓。
6 结论与展望
基于土-结构相互作用以及结构-土-结构相互作用的研究成果,相关学者对SCI效应的研究开展了许多工作,取得了显著的进步。目前得到的主要结论有:
(1)SCI效应受到城市建筑密度、结构空间分布形式、动力特性、间距、土-结构刚度比、土与结构中剪切波速比、结构高度和土层厚度或表层土厚度比等因素的影响。
(2)位于刚性土层上质量轻、刚度小、较为分散的结构群相互作用较小;而位于柔性土层上重型、刚性、密集的结构群相互作用显著。
(3)城市效应可能导致响应持时的增加、响应幅值的变化、空间相干性减小、产生拍振的现象等。
(4)城市效应导致城市内部响应整体上减小(部分位置增大),城市外部响应略微增大,且对边界处的影响显著,较小的建筑物在边界处可能遭受严重破坏。
(5)当城市固有频率与场地表层土固有频率一致时,SCI效应最为显著。
已有研究大部分是针对二维城市模型的SCI效应,尤其是二维单层均质土上的周期性城市的研究。而对于考虑真实土层分布的非周期性三维城市模型的SCI效应的分析较少。所以与实际城市环境相比,已有研究工作具有一定的局限性。因此,可对场地-城市效应的研究做以下展望:
(1)更合理的结构分析模型和更真实城市模型。已有研究大多将结构简化为矩形实体块模型或带有刚性浅基础的单自由度体系模型,且未考虑材料的非线性行为。而在地震作用下结构往往已经进入非线性状态,可能使建筑群的振动频率发生变化,进而影响其地震响应。另外,结构的基础形式、方向性、分布形式等与场地-城市效应相关的因素常被忽略或简化考虑。因此,还需进一步开展对相关因素的研究。
(2)地下结构的影响。已有研究中较少考虑地下结构的存在,而随着城市的发展,地铁车站和隧道、综合管廊、换乘车站、地下枢纽以及其他复杂地下空间结构越来越多,导致大量地下交叉结构涌现,而地表结构往往带有地下室,因此大型复杂地下结构(群)对SCI效应的影响不容忽略;
(3)地震波输入方式。现有研究很少考虑到地震动输入的空间变化性。由于场地-城市效应研究涉及的场地范围通常达到几千米甚至几十千米,且城市环境较为复杂,地震动具有显著的空间变化性。因此有必要开展非一致激励下的SCI效应的研究;
(4)试验研究。考虑的城市和土体模型较为简单,且可用于理论研究的城市环境中的实测地震数据不足。因此应该提高与城市效应相关的试验设计研究,另外,可通过在真实城市环境中布置地震台阵研究波的传播规律,有利于进一步理解SCI效应的作用机制;
(5)评价方法。已有研究通过对简化城市模型的参数分析,得到了影响SCI效应的主要因素,根据相关参数提出了SCI效应的评价方法及相应的评价指标,但这些参数定义和公式的准确性还需进一步验证和完善,例如进一步考虑建筑类型、分布形式等因素的影响;
(6)超材料(Metamaterial)基本理论的应用:考虑到声子晶体型周期性结构独特的滤波特性,周期性隔震/振的概念逐步提出并获得广泛关注[61]。如果将城市中建筑群、景观树木等合理布局,考虑其周期性排列,从城市整体角度考虑其抗震/振性能和减隔震/振可能性,必将提升城市整体抗震性能。

