龙卷风导致高速列车倾覆风险评估与管理
杨庆山,左有嘉,回 忆,田村幸雄
(重庆大学土木工程学院,重庆 400045)
引言
龙卷风是小概率极端气象灾害,它能将巨大的能量汇聚于细小的涡管中释放,产生极高的风速和巨大的压差,摧毁沿途的建筑和车辆,带来重大损失。2005年6月10日发生在辽宁朝阳的龙卷风,袭击了4个村庄,导致7.1万人受灾,直接经济损失达1.2亿[1]。通常,学者们多关注于龙卷风对建筑物的破坏和影响,如低矮房屋[2]、冷却塔[3]或核电站[4]。而近年来,高铁因龙卷风的发生导致倾覆的事件引起了人们广泛关注。2005年12月25日,一辆高速行驶的日本羽越本线列车,在酒田附近遭遇龙卷风袭击,列车脱轨倾覆,造成5人死亡、32人受伤;2006年9月17日,日本九州日丰线从别府到宫崎,5辆编组的列车以25 km/h的速度慢行时遭遇龙卷风致前2辆脱轨倾覆,造成6人受伤[5]。列车倾覆不光会造成人员伤亡和车辆毁坏,还会导致铁路晚点、线路停运,降低运输效率,对多个地区产生严重影响。
此类事故也让专家们开始关心列车在龙卷风下运行安全性问题。Zhang等[6]用“列车状”长方体进行风洞试验和数值模拟,发现当列车表面风速变化剧烈时会出现“过冲现象”,风荷载会被放大。Suzuki等[7]的风洞试验,将1:40的列车模型以一定的速度通过龙卷风模拟发生器产生的涡流,测量列车表面的压力值得出风荷载变化规律。Baker等[8]建立了新的龙卷风风场模型,并在此基础上构建了不同条件下列车受力分析的数学模型。但是,目前相关研究多旨在于了解列车在龙卷风下的受力特点及风荷载变化,而关于列车运行稳定性问题研究则鲜有涉及。虽然目前看来列车遭遇龙卷风倾覆的概率很低,但是随着未来高铁技术迅猛发展,铁路密度扩大、高铁速度加快、发车数量猛增,那么此类事故就不再是“不可能事件”了。基于此,本文提出了用于分析实际条件下龙卷风致使高铁倾覆概率分析方法,为铁路的风险评估和管理提供参考,是完善铁路风灾分析方法的重要部分。
1 分析方法简述
分析步骤主要分为2个部分:龙卷风模拟和列车倾覆分析,如图1所示。目前人们对龙卷风灾害的物理过程并不完全了解,通常只能根据历史灾害事件记录和有限的数学、物理分析手段对有关规律作出较粗糙的估计[9]。而列车遭遇龙卷风后倾覆又属于小概率事件,依据目前的列车事故报告以及龙卷风数据统计量还无法进行估计,必须要扩大样本,因此文中通过蒙特卡洛模拟方法来得到足够的样本数。首先根据目标地区龙卷风气象数据拟合得到5个关键参数概率分布形式,分别为:发生位置、强度、路径长度、时间和方向,其中强度还包括了风速和龙卷风半径。然后根据相应分布形式随机模拟数值,得到龙卷风数学仿真模型[10-11]。再由铁路时间表确定列车位置,计算运行过程中和龙卷风之间的最短距离,并以风场模型[8]为基础得出最大风荷载。通过列车倾覆计算模型和倾覆准则[12]判断列车的稳定性。经过多次模拟,发生倾覆的频率即为最终龙卷风造成列车倾覆的概率。本研究提出的方法充分考虑了列车和龙卷风在时间、空间上的关系,可以用于不同地区、不同铁路的风险分析。
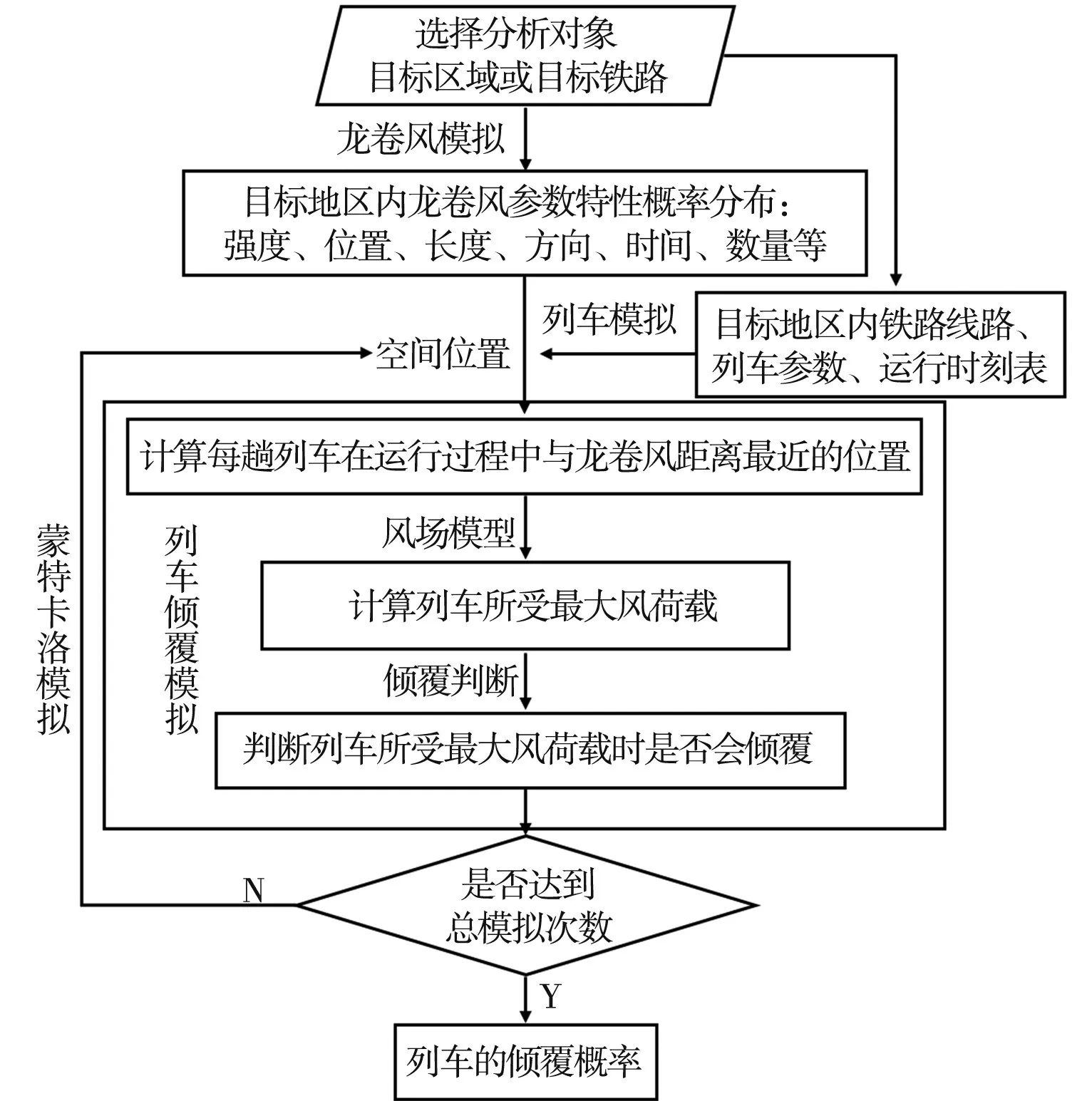
图1 列车倾覆概率蒙特卡洛模拟方法Fig.1 Monte Carlo simulation method of train overturning probability
2 龙卷风模拟
2.1 龙卷风的发生位置
模拟龙卷风发生位置的关键是确定模拟的区域。文中模拟区域是以目标铁路为中心的矩形范围,包含所有会对列车产生影响的龙卷风,所以铁路上任意一点到模拟区域边界的最短距离都应该大于最长的龙卷风路径。因此,模拟区域的大小和位置是由铁路上经纬度坐标最大和最小的点来确定。确定模拟区域之后,龙卷风的发生位置则在区域内服从经度和纬度的二维均匀分布。
2.2 龙卷风强度
Brooks等[13-14]通过对世界多个地区龙卷风数据统计分析得出龙卷风的强度服从威布尔(Weibull)分布。威布尔分布的概率密度分布函数以及累计概率分布函数如下:

式中:x表示龙卷风强度;α是形状参数(shape parameter);β是比例参数(scale parameter)。
2.3 龙卷风风速和最大风速半径
龙卷风的最大风速(Vmax)与强度x的关系如下[13]:

Tamura等[4]在建立日本核电站的龙卷风灾害模型时,统计了日本龙卷风移动速度(Vm)、最大风速半径(Rm)和最大风速之间的关系:

龙卷风的最大风速由最大切向风速(Vmax.t)和移动速度线性叠加而成,所以可得:

2.4 龙卷风移动路径长度
龙卷风的移动路径长度是反映其强度大小的一个重要参数。龙卷风强度越大,平均移动路径越长,所以要对不同强度的龙卷风移动路径长度进行单独分析。龙卷风移动路径长度同样也服从威布尔分布[15]。
2.5 龙卷风时间
龙卷风时间包括:开始时间(TS),持续时间(TD),结束时间(TE)。开始时间根据龙卷风记录中在各时间段内发生的概率随机抽样;其他时间计算见下式,其中L表示龙卷风长度,Vm表示龙卷风移动速度:

2.6 龙卷风移动方向
大多数龙卷风移动长度和持续时间都比较短,在移动过程中方向变化很小,所以模拟时通常认为龙卷风沿直线运动[16]。文中将全方向(0°~360°)分成16段,每段间隔22.5°,坐标系假设以“东”为起点(0°),逆时针旋转为正。移动方向模拟时,根据龙卷风方向区间的概率分布随机抽样,具体角度数值在方向区间内服从均匀分布。
3 列车倾覆模拟
3.1 风速计算
列车的倾覆计算有多种方法:数值模拟[17]、风洞试验[18]、全尺寸试验[19]等。为了与蒙特卡洛模拟方法更好地契合,文中采用静态分析方法,只考虑当列车和龙卷风相距最近时是否会倾覆。依据列车的运行时刻表计算出龙卷风发生时列车出站时间差,通过铁路线路以及车速推算出当时列车的经纬度坐标,计算出两者的初始距离,并分析龙卷风生命周期内每分钟的两者距离变化,最后取最短距离(r)。列车的长度相较于龙卷风尺度无法忽略,本文假设车长400 m,取车头、车中、车尾3个特殊位置分别计算距离,并取三者中的最小值为最短距离。根据文献[8]中的风场模型,可以用最短距离计算出列车遭遇的最大风速,风场模型为:

式中:Rm表示最大风速半径;r表示龙卷风和列车的最小距离;Vmax.t和Vmax.r分别表示龙卷风最大切向速度和最大径向速度,Vt和Vr表示切向速度和径向速度;S表示龙卷风最大切向速度和最大径向速度的比值,文中取S=2。
3.2 风荷载计算
将龙卷风的风速沿列车的运动方向与车速进行叠加,得到合成风速(U)和偏航角(ψ)[20],见图2。图中(Xt,Yt)表示龙卷风中心经纬度坐标,(Xv,Yv)表示列车车头经纬度坐标,γ表示铁路与水平线的夹角;α表示龙卷风移动方向;θ表示最短距离与水平线的夹角。研究[21-23]表明龙卷风在北半球绝大多数为逆时针旋转,南半球则相反,文中以北半球为例。合成后的速度分量为:

图2 龙卷风与列车车头速度合成示意图Fig.2 Combination of tornado and train speed
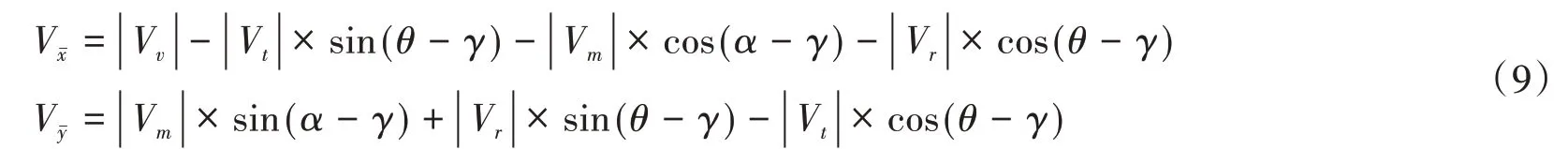
式中:V xˉ为沿轨道方向速度分量;V yˉ为垂直轨道方向速度分量,风速(U)和偏航角(ψ)为:
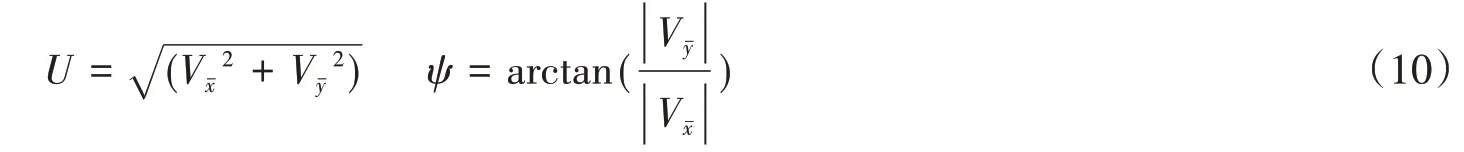
Baker等[24]根据多个列车风洞试验数据,总结出偏航角和风力系数(CRL)的关系曲线,用以分析非特殊偏航角条件下的风力系数:

式(11)、式(12)中CRL(40)、C R L(90)分别表示偏航角在40°和90°条件下的风力系数值,该值可以通过风洞试验或数值模拟计算得出。n,m表示列车的体型系数。式(13)中F表示风荷载,包括侧力FS和升力FL;CRL(ψ)表示偏航角为ψ的风力系数;ρ表示空气密度ρ=1.29 kg/m3;A表示列车参考标准面积A=10 m2。文中分析数据来自欧洲规范[25]中ICE3型列车的风洞试验,拟合得到n=1.5,m=-3。
3.3 列车倾覆计算
本文采用日比野有等[26]提出的列车临界风速静态计算模型(图3)分析列车的受力情况,相关参数释义及取值见后表3。

图3 列车倾覆计算模型Fig.3 Train overturning calculation model
在模拟过程中,列车均认为沿直线运动,不考虑轨道的超高和倾斜,忽略超离心加速度的影响,根据列车的平衡条件,对列车背风轮处求矩可得:
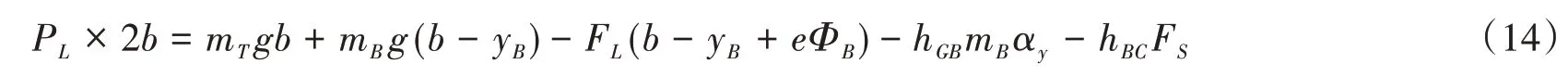
在风荷载作用下,列车的迎风轮(PL)受力会相较于静态轮重(P0)而减少,当减载值(ΔP)等于静态重时,迎风轮受力为0,轮重减载率D=1,认为列车倾覆。

如果D≥1,则认为龙卷风会造成该列车倾覆,否则认为列车为安全的。上述过程为单次模拟过程,根据总模拟数量进行重复计算,最后倾覆概率为造成列车倾覆的龙卷风的数量与模拟的龙卷风数量之比。
4 日本东海道新干线案例分析
4.1 日本龙卷风模拟
4.1.1 日本龙卷风发生位置和数量
国内龙卷风研究起步较晚,虽然不少学者也做了灾后调研[27]和数据特性分析[28],但是仍然缺少关键数据记录,导致参数概率分布拟合误差大而不利于随机抽样[29],故以日本为对象。选取日本东京到新大阪的东海道新干线作为研究对象,东海道线全长约为520 km,作为日本第一条新干线,是日本太平洋沿岸最重要的铁路线之一。
日本气象厅从1961-2015年一共统计了约1 839起龙卷风。东海道新干线位于日本关东和中部地区,根据日本气象厅网站所公布的龙卷风发生位置可以很明显地看出:日本沿海和东部内陆地区龙卷风较为频发。
根据日本气象厅统计数据,最长的龙卷风移动长度为42 km,本研究偏于保守取60 km作为最短边界距离,保证东海道线上任一点到模拟区域边界的最短距离至少为60 km,由此模拟区域为图4白色矩形框以内。区域大小约为500 km×250 km,纬度范围[34.1°N,36.3°N],经度范围[134.9°E,140.4°E]。
图4中反映出不同地区龙卷风的位置分布有明显区别,龙卷风在平原地区(灰色)发生密集,而在内陆山区(绿色)和外部海域(蓝色)则比较稀疏。为了更好地体现龙卷风的空间分布特点,文中对模拟区域做进一步划分。图5中将模拟区域均匀地划分为1 250个网格,沿经度方向分为50份,纬度方向分为25份,网格大小约为10 km×10 km。通过每个网格内龙卷风数量便可体现不同位置的龙卷风发生概率,龙卷风在每一个网格中服从经度和纬度的二维均匀分布。如果网格内没有龙卷风发生,则默认为此地区不会发生龙卷风。图6是模拟55年的龙卷风位置分布,模拟得到的龙卷风位置分布和疏密特点与实际情况基本一致。
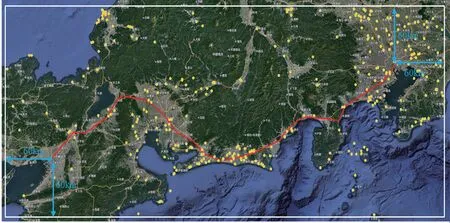
图4 东海道附近龙卷风发生位置及模拟范围Fig.4 Location and simulation range of tornado near Tokaido

图5 模拟区域网格划分Fig.5 Simulation of area meshing
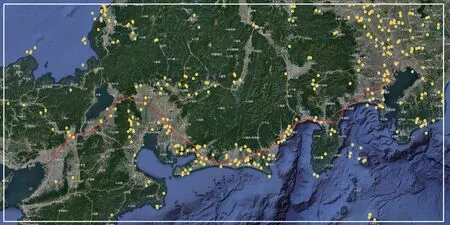
图6 模拟55年的龙卷风位置分布Fig.6 Simulation of the tornado location in 55 years
4.1.2 日本龙卷风的强度
根据式(1),由日本强度数据拟合得到威布尔分布参数为:α=1.88;β=1.36,图7是龙卷风强度拟合的概率分布,日本龙卷风强度较弱,以F0、F1为主。

图7 龙卷风强度概率分布Fig.7 Probability distribution of tornado intensity
4.1.3 日本龙卷风移动路径长度
表1是日本各强度龙卷风长度分布的威布尔参数,图8是以F0为例的数据拟合。其中由于日本F3龙卷风的样本数量过少,拟合误差较大,故将F3与F2数据合并拟合。
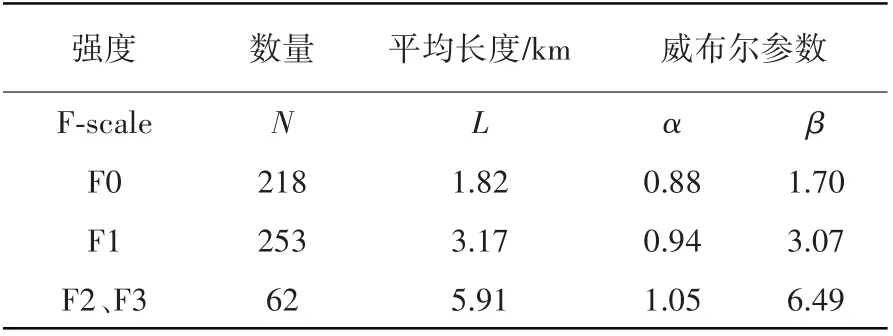
表1 各强度龙卷风长度威布尔分布参数Table 1 Weibull distribution parameters of tornado length of each intensity
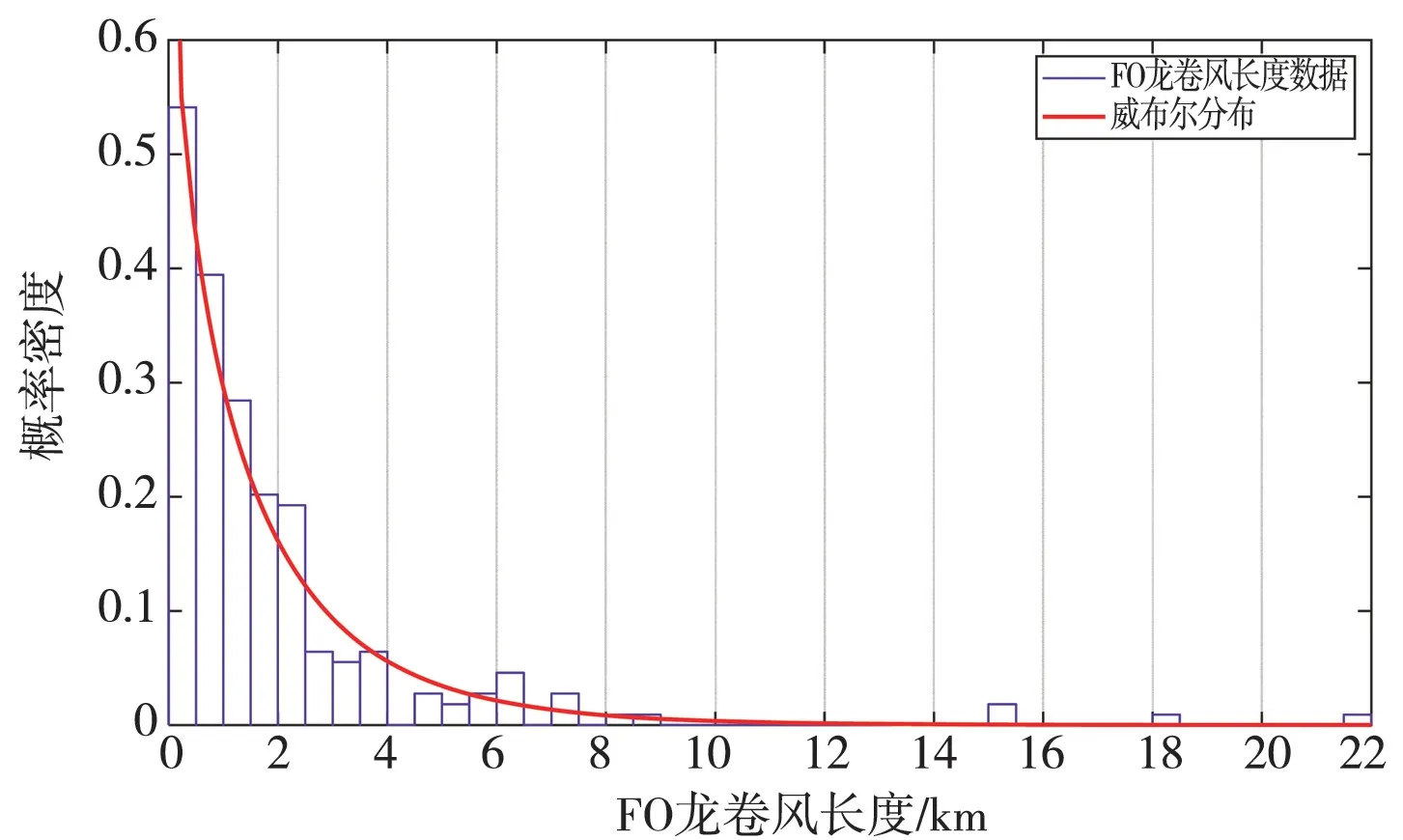
图8 F0龙卷风移动长度威布尔分布拟合Fig.8 F0 tornado moving length Weibull distribution
4.1.4 日本龙卷风时间
图9为日本龙卷风发生时间的概率分布,下午2点~5点是日本龙卷风的高发期,约有31.5%的龙卷风发生在此时段,尤其是下午3点~4点的发生概率达到9.3%,是“最危险”时刻。
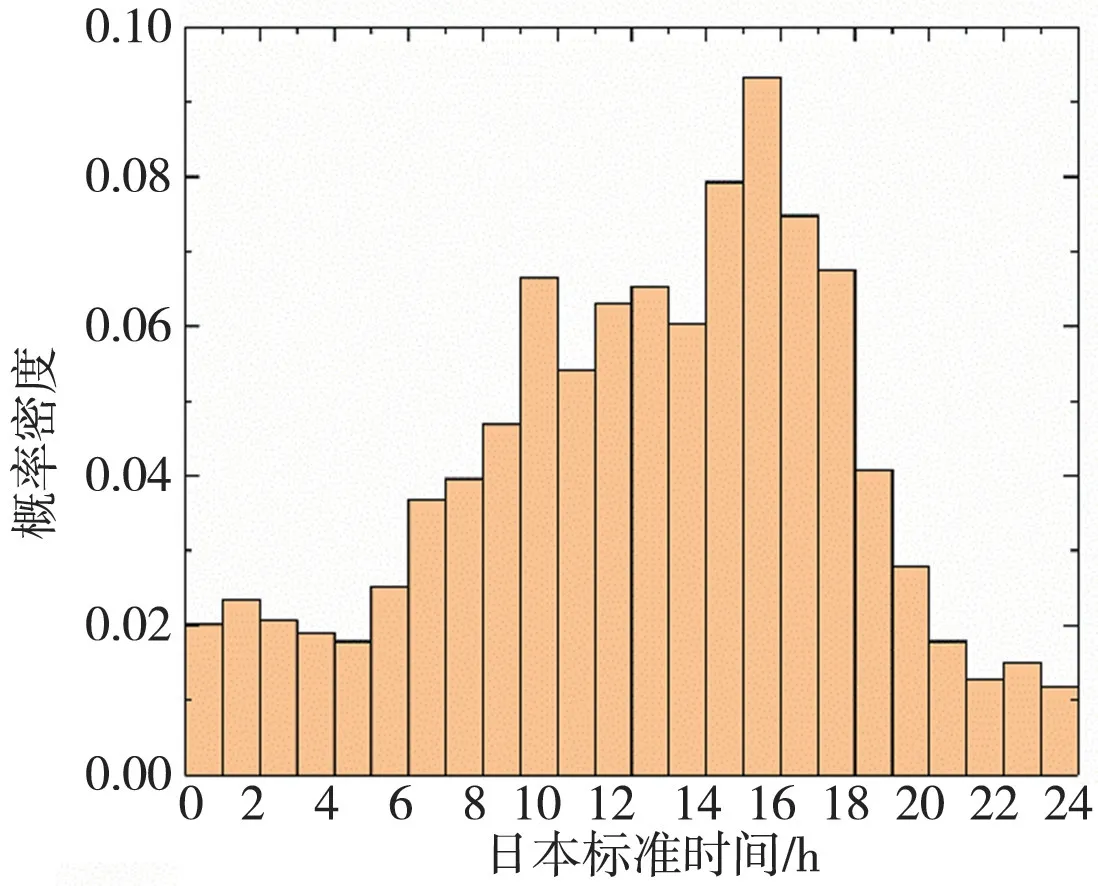
图9 龙卷风发生时间分布Fig.9 Time distribution of tornado occurrence
4.1.5 日本龙卷风移动方向
表2为每个方向代表的角度范围与相应的龙卷风发生概率,有68.4%的龙卷风都向东北方向移动。

表2 龙卷风移动方向角度范围及发生概率Table 2 Angle range and probability of tornado movement direction
4.2 列车模拟
4.2.1 列车时刻表
在JR东海铁路公司的列车时刻表上,高铁的运行方式为3种:(1)希望号,停靠主要大城市站点,每天187辆,行驶全程约为148 min,平均车速211 km/h(59 m/s);(2)光号,停靠大、中城市,每天29辆,行驶全程约为174 min,平均车速179 km/h(50 m/s);(3)回声号,停靠所有城市站点,每天11辆,行驶全程约为234 min,平均车速133 km/h(37 m/s)。上述数据统计时只包括运行范围是新大阪到东京整个区间的单程车辆,并对模拟列车运行时刻表时做了以下假设:
(1)每种列车的发车间隔保持一致。希望号发车时间为6:00~21:30,每辆车间隔5 min;阳光号发车时间为6:18~20:48,每辆车间隔30 min;回声号发车时间为8:54~18:54,每辆车间隔60 min。
(2)列车的每天运行状况均相同,不考虑特殊情况下的停运或修理。列车运行时不考虑车站停靠的时间且全程速度不变,每个车站的时间节点根据站点间的距离比例划分。
4.2.2 列车计算参数
文中列车的计算参数见表3[30-31]。
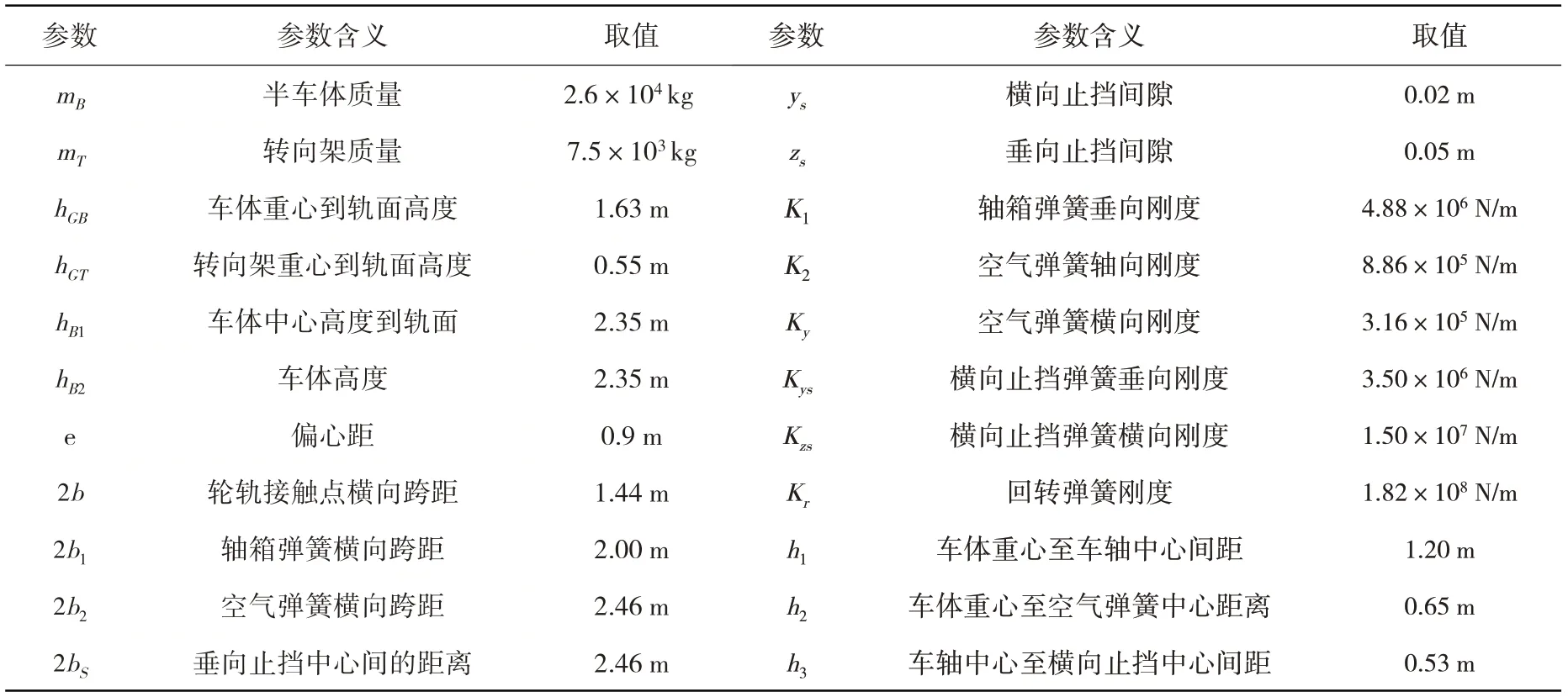
表3 计算车辆参数Table 3 Vehicle parameters
4.3 模拟结果
本研究模拟了50 000年,全日本发生龙卷风次数约为805 000,模拟区域内总模拟次数为150 000。分析显示,在模拟区域内龙卷风穿过东海道新干线的概率为2.8%,平均每12年发生一次;龙卷风造成列车倾覆的概率为4.4×10-4,平均每760年发生一次。而从整体角度看,全日本每发生一次龙卷风,其穿过东海道新干线的概率为5.3×10-3,造成倾覆的概率为8.1×10-5。
5 影响参数分析
为了分析列车参数对行车安全的影响,文中选择了列车的发车间隔、行驶速度作为分析对象。模拟条件为:车长400 m,运行时间为6:00~18:00,列车类型只有一种,发车间隔分别为1、2、3、4、5、6、10、12、15、20、30分钟;车速为25 m/s、50 m/s、75 m/s,模拟年数均为50 000年。如图10所示,列车的倾覆概率与列车发车间隔呈反比。根据图中所示,当发车间隔为1 min时,每小时列车数量为60,25 m/s、50 m/s、75 m/s车速下倾覆概率分别为2.4×10-4、3.35×10-4、4.0×10-4;当发车间隔增加至5 min时,每小时列车数量减少到12,倾覆概率分别下降到为5.5×10-5、6.02×10-5、7.68×10-5;而当发车间隔进一步增加到30 min时,每小时列车数量仅为2,倾覆概率分别降低至0.87×10-5、1.16×10-5、1.27×10-5。对比之后发现,发车间隔从1 min增加到5 min,每小时列车数量下降5倍,倾覆分别下降了4.3、5.5、5.2倍;而发车间隔从5 min增加到30 min,每小时列车数量下降6倍,倾覆分别下降了6.3、5.2、6倍。这证明了单位时间内列车的数量与倾覆概率大致呈线性正相关(图11),经过拟合得到3种车速下列车数量与倾覆概率的函数关系:
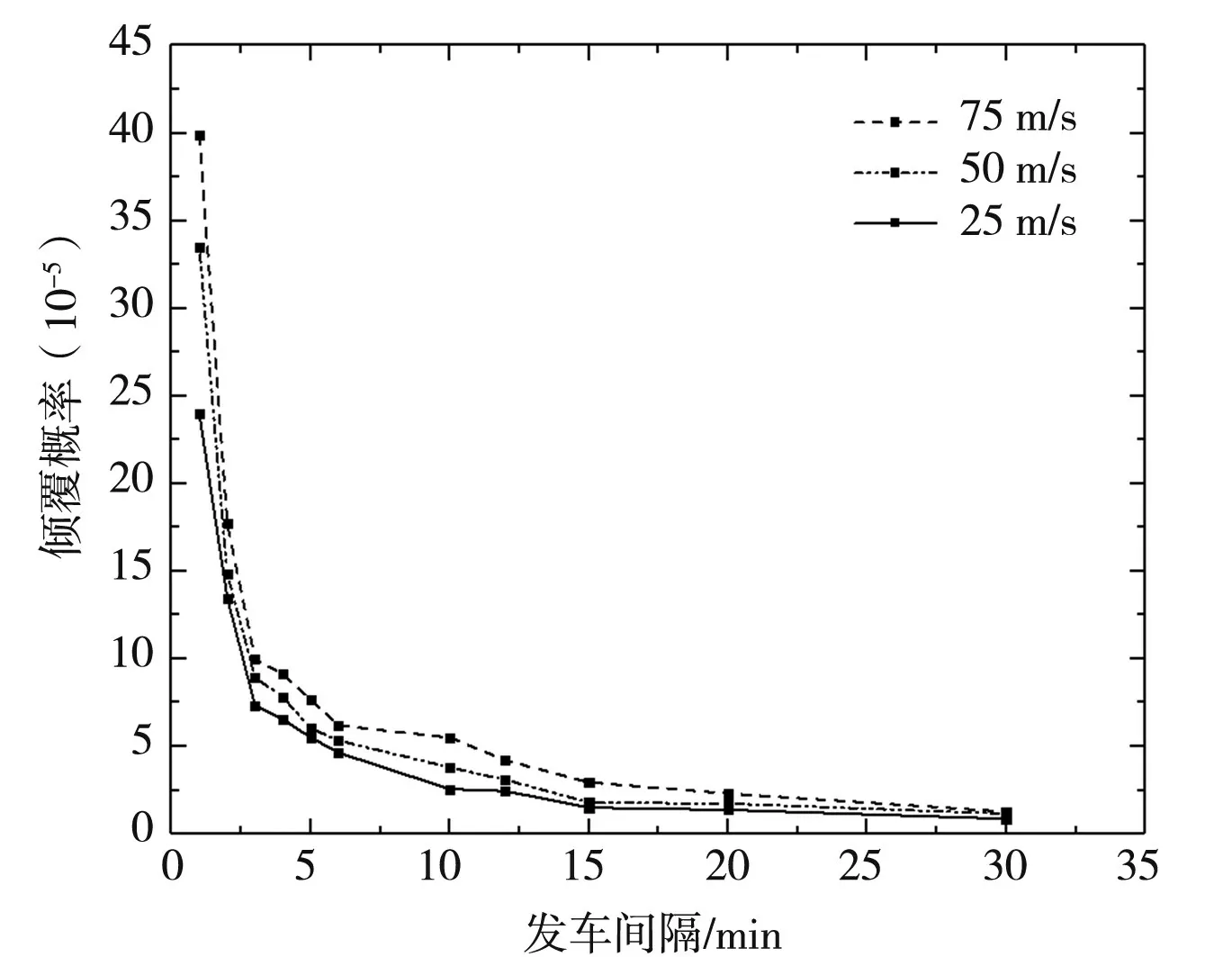
图10 不同车速下倾覆概率与发车间隔关系Fig.10 Relationship between overturning probability and departure interval at different speeds
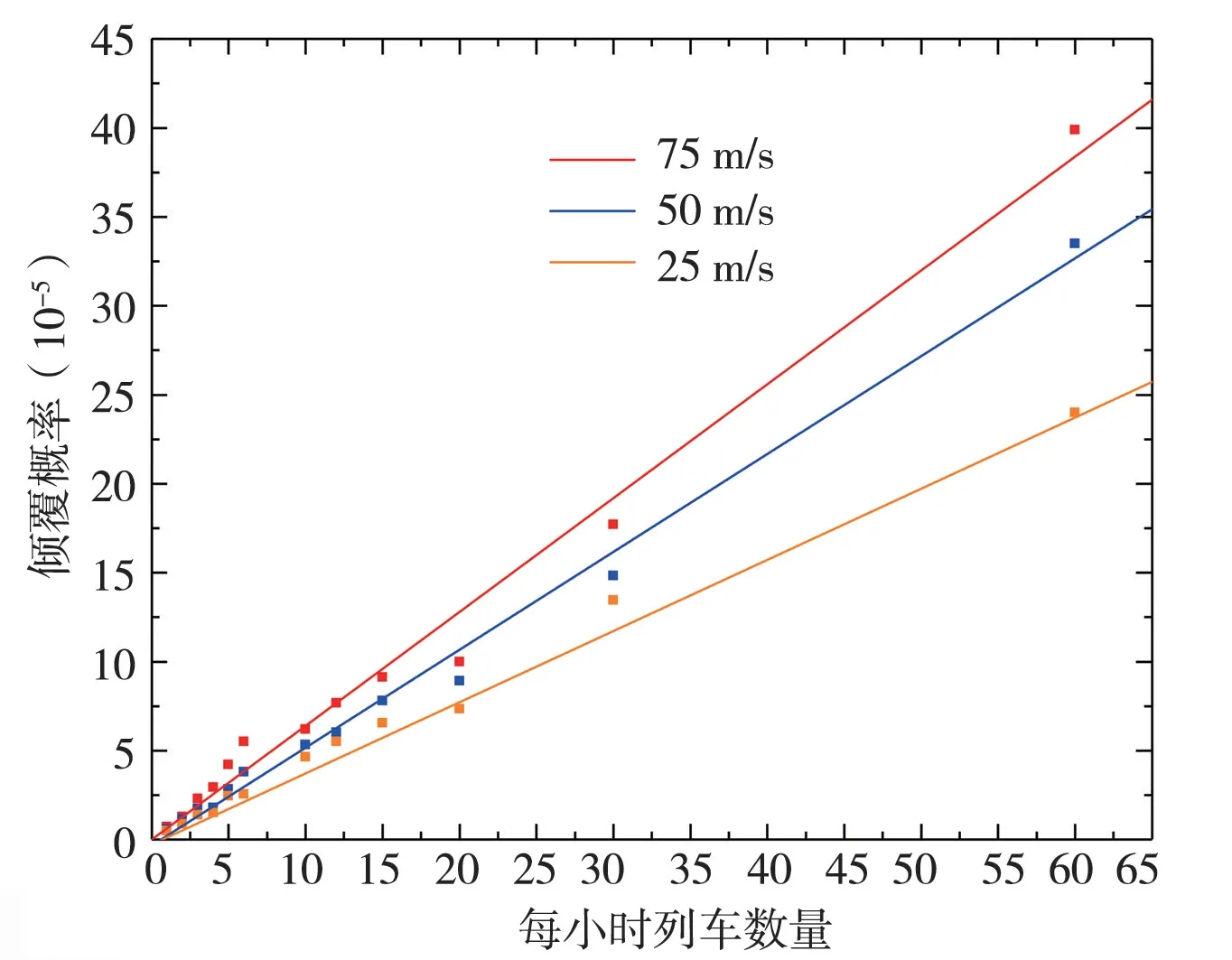
图11 不同车速下倾覆概率与每小时列车数量关系Fig.11 Relationship between the overturning probability and the number of trains per hour at different speeds
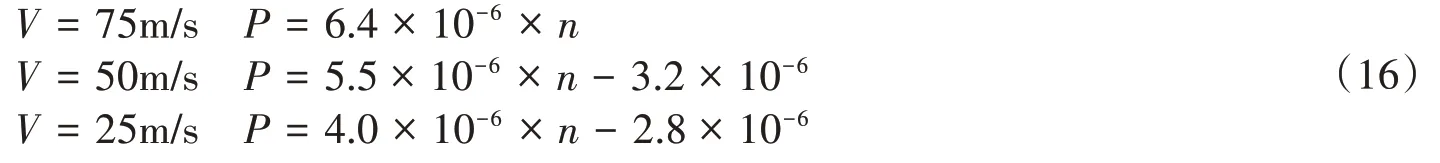
式中,P表示倾覆概率,n表示每小时列车发车数量n=60/T,T表示发车间隔(min)。车速越快,直线斜率越大,倾覆概率随列车数量的变化也越快。当列车首尾相连,“零间距运行”时,25 m/s、50 m/s、75 m/s车速下理论的最大倾覆概率分别为4.32×10-3、2.48×10-3、9×10-4。
基于上述的计算结果并结合龙卷风的时间分布规律,铁路部门可以通过调整列车的时刻表以达到降低风险的目的。假设运行时间6:00~18:00,全天发车间隔为6 min,此时倾覆概率约为5.18×10-5。由图9可知,上午龙卷风发生概率远低于下午,所以当发车时间变为6:00~11:00间隔5 min,11:00~18:00间隔7 min,列车总数量不变,而倾覆概率降为4.2×10-5,风险降低了19%,安全性明显提高。所以根据本方法,可以在保证运输效率不变的前提下调整运行时间,降低事故发生概率。另外,文中只选择了一条铁路进行分析,本方法可以对某地区所有铁路网进行模拟得到整体概率分布,在高风险地区设立监测系统,最大程度上提高监测效率,节约成本。上述措施可以有效加强社会的防灾减灾能力建设,这也是应对日益复杂的自然灾害和减轻灾害风险最有效的途径和手段[32]。
6 结论
本研究为对列车在龙卷风灾害下的倾覆风险进行评估,通过蒙特卡洛模拟,建立了龙卷风作用下列车倾覆概率估计方法。考虑了实际情况下龙卷风的时间和空间的分布特点,对龙卷风的各项参数建立了概率模型,以此为基础进行列车的倾覆判断,并以日本东海道新干线为例计算得出龙卷风穿过该线路的概率为5.2×10-3,该条线路列车遭遇龙卷风倾覆概率为6.9×10-5,龙卷风穿过铁路时会有0.75%的概率造成列车倾覆。同时,分析了列车不同参数对倾覆概率的影响,发现列车的倾覆概率与发车间隔呈反比,与单位时间列车数量呈线性正相关,拟合得到了不同车速下倾覆概率与单位时间列车数量的函数关系,并在此基础上估计25 m/s、50 m/s、75 m/s车速下理论的最大倾覆概率分别为4.32×10-3、2.48×10-3、9×10-4。文中提出了调整列车运行时刻表来有效降低列车倾覆风险,还可以通过整体分析结果进行监测系统的布置,提高效率,降低成本。随着高铁网络的进一步扩展,本方法在后续地区性乃至全国性铁路风险分析中都能够提供很好参考和支持。
另外,由于目前列车和龙卷风之间气动力关系的研究还处于探索阶段,相关原理还不是很明确,所以选择了横风风场叠加计算风荷载方法,但难免会有些不准确。在相关研究成熟之后,可以对本方法中的受力分析和倾覆计算部分进行替换和修缮,提高结果精确性。当对某一具体型号列车分析时,也可以使用其龙卷风风洞试验数据进行代替。

